Измерение толщины Z-срезов одноосных кристаллов на основе лазерных пучков Бесселя

Измерение оптических и размерных характеристик одноосных кристаллов наиболее часто осуществляется поляризационно-интерференционными методами [1 –5]. Общим признаком этих методов является использование схемы «поляризатор – кристалл – анализатор». Такая схема обуславливает интерференцию обыкновенного и необыкновенного пучков за анализатором, по виду которой определяют толщину и двулучепреломление кристалла. Как правило, для диагностики X -срезов одноосных кристаллов используют коллимированное излучение, а для Z -срезов – сходящийся пучок, формирующий коноскопическую фигуру, или коллимированный пучок в сочетании с поворотом кристалла [5].

Однако для измерения толщины и двулучепреломления одноосных кристаллов может использоваться иной принцип, заключающийся в пропускании через кристалл специальных лазерных пучков [6– 18], формируемых дифракционными оптическими элементами. При этом в кристалле наблюдается деполяризация и интерференция множества дифрагировавших лучей, распространяющихся под разными углами к оптической оси одноосного кристалла [18]. В результате распределение интенсивности в сечении выходного пучка определяется ориентацией оптической оси, двулучепреломлением и толщиной кристалла. Исследование оптических и размерных характеристик одноосных кристаллов, таким образом, основано на анализе изображения выходного пучка. Например, на измерении распределения интенсивности или размеров характерных максимумов интенсивности. Это позволяет использовать стандартные средства фотометрии. С другой стороны, стоимость дифракционных оптических элементов невелика, а высокая точность их изготовления позволяет осуществить прецизионные измерения.

Целью работы являлось измерение толщины плоскопараллельного одноосного кристалла Z -среза с использованием лазерных пучков Бесселя.

Выбор именно пучков Бесселя обусловлен несколькими причинами. Во-первых, пучок Бесселя 0-го порядка, используемый для освещения кристалла, легко получить с помощью круговой дифракционной решётки (дифракционного аксикона) [19–22]. Во-вторых, пучки Бесселя имеют осесимметричную форму, что упрощает математическую обработку изображения пучка на выходе кристалла.

1.    Физические основы измерения

Схема измерения толщины показана на рис. 1.

Z-OCb

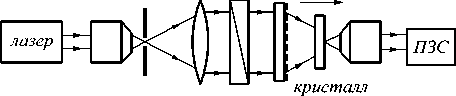
Рис. 1. Оптическая схема для измерения толщины Z -среза одноосного кристалла

Излучение лазера проходит пространственный фильтр – расширитель пучка, коллимируется и поляризуется. Дифракционный аксикон, освещаемый коллимированным излучением, формирует сходящийся конический пучок – пучок Бесселя 0-го порядка, образованный центральным максимумом интенсивности и набором окружающих колец ненулевой интенсивности. При распространении в оптически однородном пространстве пучок Бесселя сохраняет поперечное распределение интенсивности. Однако при распространении в Z-срезе одноосного кристалла происходит периодическое преобразование тёмных и светлых участков в поперечном распределении интенсивности [6– 12]. Это соответствует взаимному преобразованию пучков Бесселя 0-го и 2-го порядков, описываемых в рамках скалярной теории, например, с помощью интегрального оператора распространения [11, 12]. Расстояние p, соответствующее переходу пучка Бесселя 0-го порядка в пучок Бесселя 2-го порядка, зависит от числовой апертуры дифракционного акси-кона и двулучепреломления одноосного кристалла. Для измерения толщины поперечное распределение интенсивности выходного пучка фиксируется видео- камерой. Далее оно сравнивается с таблицей эталонов на основе математической модели распространения пучков Бесселя в одноосном кристалле. Это предъявляет высокие требования к пространственному разрешению, линейности и разрядности аналого-цифрового преобразователя (АЦП) видеокамеры, которая в значительной степени определяет точность и разрешающую способность измерения.

Для расчёта поперечного распределения интенсивности пучка Бесселя на выходе Z -среза одноосного кристалла воспользуемся интегральным оператором распространения, полученным ранее в [11]. В качестве примера выберем кристалл конгруэнтного ниобата лития Z -среза с показателями преломления n o = 2,28634, n e =2,20267, длину волны лазерного пучка λ 0 =632,8 нм, период дифракционного аксикона d =4 мкм. Поперечные распределения интенсивности при различных толщинах кристалла h показаны на рис. 2.

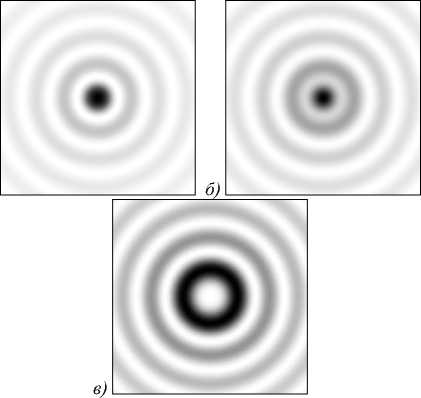
Рис. 2. Поперечное распределение интенсивности пучка Бесселя на выходе Z-среза одноосного кристалла: h = 0 (а), h = 0,5p (б), h = p (в)

Для малой толщины кристалла h <<  p наблюдается преимущественно пучок Бесселя 0-го порядка, содержащий выраженный центральный максимум интенсивности. При толщине h ≈ p наблюдается пучок Бесселя 2-го порядка с центральным минимумом интенсивности. При толщинах h >  p пучок Бесселя 2-го порядка будет вновь переходить в пучок 0-го порядка. Таким образом, полупериод пространственного преобразования пучка Бесселя p соответствует максимальной толщине кристалла, при которой обеспечивается однозначность измерения. Значение p , отсчитываемое вдоль Z -оси кристалла, приближенно равно [12]:

Р = М2(Тo -Ye )) ,                          (1)

где γ o , γ e – величины, определяющие направление распространения обыкновенного и необыкновенного пучков:

Y o = 4n o ^a 2 , Y e = 7 n 2 ^-a 2 n 2 / n 2 ,               ⁽²⁾

где α = arcsin (λ 0 / d ) – числовая апертура дифракционного аксикона с периодом d , освещаемого коллимированным лазерным излучением с длиной волны λ 0 .

Приведённые формулы (1), (2) являются оценочными, поскольку их погрешность составляет несколько процентов по сравнению с использованием интегрального оператора распространения пучка Бесселя в одноосном кристалле [11]. Однако они позволяют приближённо вычислить максимальную измеряемую толщину h ≤ p для выбранного кристалла при использовании одного аксикона. Соответственно, перед оптическим измерением необходимо оценить толщину кристалла каким-либо другим методом, например, электронно-механическим. Это измерение необходимо для проверки условия h ≤ p .

Следует отметить, что максимальная измеряемая толщина кристалла также не превосходит расстояния L , на котором пучок Бесселя сохраняет свою поперечную структуру (модовые свойства). Для дифракционного аксикона радиусом r и периодом d , освещаемого длиной волны λ 0 и кристалла с усреднённым показателем преломления n , это расстояние не превышает L ≤ r /tg(arcsin(λ / d )) ≈ rnd / λ 0 . Данное ограничение не так существенно, как предыдущее, в плане измеряемых толщин кристаллов. Это объясняется тем, что радиус изготавливаемых дифракционных ак-сиконов достигает 100– 150 мм, а период аксикона d и используемая длина волны λ 0 могут изменяться в широких пределах. Однако это условие ограничивает сверху расстояние между изображающей линзой (объективом) и кристаллом.

2.    Экспериментальное исследование

Для формирования пучка Бесселя 0-го порядка был изготовлен амплитудный дифракционный акси-кон диаметром 40 мм на стеклянной подложке толщиной 3 мм с периодом колец d =4 мкм (для λ 0 = 632,8 нм числовая апертура α = 0,16). Конструкция аксикона была образована маской Cr, сформированной методом термохимического окисления на станции круговой лазерной записи CLWS-200 с последующим удалением немаскированных участков. Согласно формулам (1), (2), максимальная измеряемая толщина кристаллов ниобата лития h для изготовленного аксикона и длины волны 632,8 нм не превосходит p =739 мкм. Расчёт по точным формулам [12] дает значение p =745 мкм.

Для экспериментального исследования использовались плоскопараллельные полированные кристаллы конгруэнтного ниобата лития Z-среза толщиной 514±2 мкм и 554±2 мкм (измерено цифровым микрометром МКЦ-25). В качестве источника излучения использовался одночастотный гелий-неоновый лазер. Лазерный пучок проходил пространственный фильтр – расширитель пучка, содержащий микрообъектив 20×, отверстие диаметром 15 мкм и линзу с фокусным расстоянием 200 мм. Излучение лазера, освещающее дифракционный аксикон, поляризовалось призмой Глана–Тейлора апертурой 10×10 мм2 с коэффициентом поляризации не менее 106. Для наблюдения выходного пучка Бесселя применялся микрообъектив 40× с числовой апертурой α = 0,65, превосходившей числовую апертуру аксикона α = 0,16, и ПЗС-матрица DCM310 с разрешением 2048×1536 пикселей и разрядностью АЦП 8 бит.

Юстировка оптической схемы заключалась в установке нормального падения лазерного излучения на поверхность дифракционного аксикона и установленного после него кристалла. Для оценки относительной погрешности δ, вызванной отклонением падения излучения на кристалл от нормального, можно использовать формулу δ≈ (1 –cos β) /cos β, где β – угол преломления в кристалле. Кроме этого, необходимо обеспечить высокое качество коллимации лазерного излучения на выходе пространственного фильтра – расширителя пучка. При наличии сферичности волнового фронта освещающего пучка, вносимой выходной линзой коллиматора, нарушается периодичность преобразования пучка Бесселя в кристалле. Особенно сильно этот нежелательный эффект заметен для кристаллов толщиной в единицы – десятки миллиметров [18, 25]. Для качественной коллимации излучения применялся датчик волнового фронта (датчик Гартмана). Освещение аксикона должно быть равномерным, для чего использовались диафрагма малого диаметра и длиннофокусная.

Фотографии выходных пучков Бесселя для конгруэнтных кристаллов ниобата лития Z -среза различной толщины показаны на рис. 3.

• а)    б)

Рис. 3. Пучок Бесселя на выходе кристаллов ниобата лития Z-среза: h=514 мкм (а), h=554 мкм (б)

Наблюдаемая на рис. 3 интерференционная картина формируется преимущественно дифракционным аксиконом за счёт отражения между передней стеклянной поверхностью подложки и частично хромированной поверхностью, обращённой к кристаллу. Для снижения интерференции следует использовать фазовые аксиконы с просветлением передней или обеих поверхностей. Замена амплитудного аксикона на фазовый также повышает энергетическую эффективность формирования освещающего кристалл пучка Бесселя 0-го порядка. Интерференция в кристалле также может быть ослаблена за счет использования длин волн диапазона 312–316 нм, в котором ниобат лития является частично поглощающим.

Из полученных экспериментальных данных следует, что увеличение толщины кристалла с h =514 мкм до h =554 мкм приводит к более полному преобразованию падающего излучения в пучок Бесселя 2-го порядка. Это хорошо видно на примере центрального максимума, интенсивность которого уменьшилась в случае более толстого кристалла. Следует добавить, что наибольшая чувствительность интенсивности выходного пучка к толщине имеет место при h ≈ 0,5p. Это объясняется тем, что зависимость центрального максимума интенсивности от толщины пропорциональна cos2(0,5πh/p).

На рис. 4 показано измеренное и расчетное поперечное распределение интенсивности для кристалла с толщиной h = 554±2 мкм. Для определения толщины кристалла из рис. 3 б выбиралось несколько (обычно 20–30) радиальных сечений, ориентированных под различными углами, которые затем усреднялись в одно поперечное распределение интенсивности. Установлено, что эксперимент наилучшим образом соответствует расчетам при толщине кристалла 554,5 мкм, что соответствует полю допуска микрометра МКЦ-25.

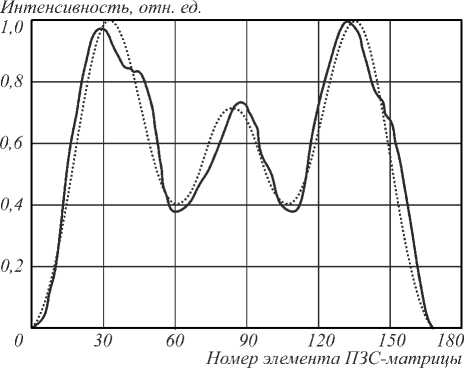
Рис. 4. Поперечное распределение интенсивности: сплошная линия – эксперимент для кристалла с h = 554 мкм, точечная – расчет для кристалла с h = 554,5 мкм

Оценим точность выполненного измерения. Периодическая зависимость интенсивности в центре пучка I 0 ~ cos²(π h /2/ p )), а интенсивности первого прилежащего кольца I 1 ~ sin²(π h /2/ p )). Выразим искомую толщину кристалла h , обозначив через I 01 отношение интенсивностей I 0 / I 1 :

Расчет абсолютной погрешности Δ h проведем формуле для некоррелированных величин [23]:

по

N h <± I

( dh , Y ( dh .

+ I 3—A no I +1 3—A ne

(dno 7 (dne

2 V/2

,

+

,

где Δ I 01 – погрешность нелинейности фотоприемника; Δ d – погрешность изготовления периода аксикона, м;

Δλ0– нестабильность длины волны лазера, м; Δno, Δne – погрешности измерения показателей преломления кристалла. При записи (4) полагалось, что погрешность задания числовой апертуры пучка α определяется только неточностью изготовления периода аксикона d. Этот случай имеет место для качественной коллимации излучения, контролируемой датчиком Гартмана или интерференционным методом. Отклонения величин для использованного оборудования равны: ΔI01 =0,03, Δd =0,1 мкм [24], Δno= Δne= 10-4, Δλ0=2∙10-6 нм при номинальных значениях d =4 мкм, no=2,28634, ne=2,20267, λ0=632,8 нм. При указанных характеристиках расчетные погрешности для h =554 мкм равны: (∂h / ∂d) Δd =5 %, (∂h / ∂I01) ΔI01=2,3 %, (∂h /∂no)Δno=0,1%,(∂h /∂ne)Δne=0,1%,(∂h / ∂λ0)Δλ0<0,01%. Однако погрешность (∂h / ∂d) Δd, обусловленная неточностью изготовления периода аксикона, является знакопеременной для множества непрозрачных колец, образующих дифракционную маску. Поэтому ее формальная оценка по (3), (4) значительно завышена. С другой стороны, в проведенном эксперименте величины I0 и I1 достаточно близки. Это существенно снижает влияние нелинейности камеры (∂h / ∂I01) ΔI01, поскольку вносимые в I0 и I1 близкие мультипликативные погрешности слабо искажают характеристическое отношение I0/ I1. Из этого следует, что наилучшая точность будет достигаться при I0= I1 или h ≈ p /2. Приближенное выполнение этого условия позволило снизить погрешность до 0,1 %. При этом погрешности измерения, вызванные дискретностью АЦП современных видеокамер (10–12 бит), также близки к этому значению.

Оценим диапазон измеряемых толщин на примере кристаллов ниобата лития при условии использования одного дифракционного аксикона. Отметим, что повышение числовой апертуры аксикона α, главным образом за счёт уменьшения периода d , приводит к уменьшению максимальной измеряемой толщины p ≥ h . Для метода электронно-лучевой литографии минимальный период d составляет около 0,8 мкм при радиусе аксикона до 200–250 мкм. При использовании метода лазерного термохимического окисления хрома, реализуемого на установке CLWS-200, наименьший период аксикона составляет ~1,3 мкм при радиусе аксикона до 100 мм. Для кристалла нио-бата лития это дает минимальные верхние пределы измеряемых толщин p ≈ 20 мкм и p ≈ 70 мкм на λ = 632,8 нм. Увеличение предельной измеряемой толщины p до единиц – десятков миллиметров достигается простым уменьшением периода аксикона.

Заключение

Выполнено измерение толщины Z-срезов дву-лучепреломляющих кристаллов, основанное на периодическом взаимном преобразовании пучка Бесселя при распространении вдоль оптической оси. Аппаратную основу измерения составляют дифракционный аксикон, стандартная лазерная и фотометрическая техника. Диапазон измеряемых толщин определяется угловой апертурой освещающего пучка Бесселя и для кристалла ниобата лития составляет единицы – десятки микрометров и более. Применение моторизованного координатного стола и программных средств обработки изображения делает возможным составление карт распределения оптических и размерных характеристик по площади кристалла.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, а также грантов РФФИ 16-29-11698-офи_м, 16-07-00825.