Измерение времени распространения продольных и поперечных акустических волн в твердых телах

Величина скорости распространения акустических волн в твердых телах определяется их структурными и упругими характеристиками, поддерживающими волновое движение, и поэтому является одним из важнейших диагностических параметров при исследовании этих сред [1, 2].

В работе рассматриваются две методики измерения времени распространения звука в твердых аморфных телах – импульсная и фазовая. Блок-схема установки для обоих методов представлена на рис. 1.

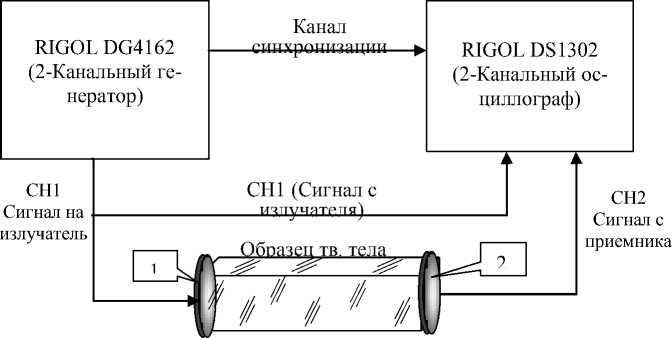
Рис. 1. Блок-схема установки для измерения времени распространения акустических волн импульсным и фазовым методом: 1 – излучающий акустический преобразователь, 2 – принимающий акустический преобразователь

Двухканальный цифровой генератор RIGOL DG4162 может выдавать на обоих каналах до 150 различных форм сигналов с частотой до 160 МГЦ, из которых нас будут интересовать для импульсного метода сигналы в виде прямоугольных импульсов малой длительности и синусоидальные сигналы для фазового метода.

Цифровой двухканальный стационарный осциллограф-анализатор RIGOL DS1302 с полосой пропускания 300 МГц и встроенным частотомером позволяет с помощью курсора измерять время сигналов на обоих каналах с точностью до 3 нс. Эта возможность использована нами в импульсном методе. В фазовом методе нами использована возможность данного осциллографа преобразовывать аналоговые сигналы каналов в цифровые с частотой дискретизации 2 ГГц и сохранять его в своей памяти в виде массива данных до 5200 значений. Скорость звука c в обоих методах может быть найдена на основе измерения времени t , которое волна затрачивает на прохождение расстояния х , равное длине образца: t= χ /c (1). В импульсном методе волна возбуждается коротким импульсом прямоугольной формы (< 0.1 мкс), подаваемым на акустический преобразователь (рис. 1). Волна имеет четкую локализацию во времени и в пространстве, что отчетливо просматривается (рис. 2) на экране осциллографа, на входы которого поданы сигналы от преобразователей. Верхний сигнал на рис. 2 получен от источника волн, а нижний от приемника. Также, внизу экрана (рис. 2) видно значение времени 51,60 µс, измеренное с помощью курсора на экране осциллографа между двумя одинаковыми по порядку пиками осциллограмм от источника и приемника волн при комнатной температуре 22 ^оC.

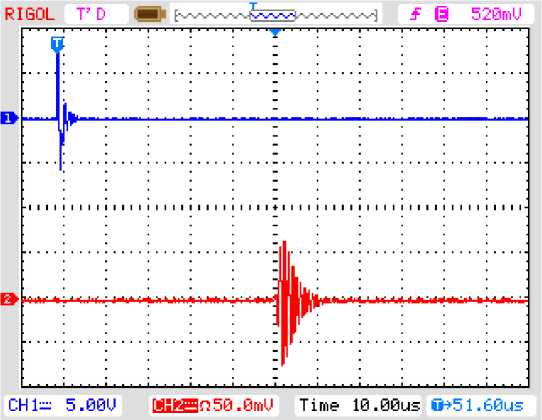
Рис. 2. Осциллограммы от акустических преобразователей на образце твердого тела. Верхняя- от источника, нижняя-от приемника. Внизу экрана осциллографа: 5В на деление шкалы для 1 канала, 50 мВ на деление для 2 канала, 10 µс на деление по горизонтали для обоих каналов, 51,6 µс – время между двумя положениями курсора (двумя одинаковыми по порядку пиками верхней и нижней осциллограмм), отмечаемых пользователем

Для реализации фазового метода измерения скорости звука используется та же установка, что и в импульсном методе (рис. 1). На акустический преобразователь-источник 1 подаются от генератора RIGOL DG4162 сигналы синусоидальной формы. Эти же сигналы подаются на вход канала 1 осциллографа. Гармоническая волна за время t проходит образец длиной х и возбуждает в приемнике-преобразователе синусоидальные сигналы, подаваемые на вход канала 2 цифрового осциллографа.

Сигналы с обоих каналов записываются в память осциллографа в виде двух массивов дискретных данных. Время t может быть измерено однозначно, если оно не превышает периода волны, т.к. увеличение числа периодов еще на один период, входящий в t, не меняет вида гармонической волны.

Фаза волны, распространяющейся в положительном направлении оси x , имеет вид:

ϕ (x,t) = ω t – kx + ϕ 0

На источнике фаза волны (при x =0) равна ϕ (0,t)= ω t + ϕ 0 . Тогда разность фаз Δϕ между сигналами источника и приемника не зависит от времени и является при постоянном расстоянии х в твердом теле линейной функцией частоты f :

л<р = <р(0, t) - ф(х. t) = kx = -^fx

В твердом теле на расстоянии x между источником и приемником измеряется зависимость сдвига фаз Δϕ от частоты f, и из наклона получившейся прямой вычисляется время:

х i d

¹ c xit d С/У                                        (4)

Разность фаз Δφ можно вычислить из массивов дискретных данных, записанных в файлы на ПК [3-4]. Для этого необходимо эти данные представить в частотном представлении с помощью дискретного преобразования Фурье:

N-i                 N-i

X(kdf) = ^ x(ndt)e"‘^,md^^dt = ^ xtndt") ^cos^(kndfdt') — ismQardfdf)')

где N – количество компонентов разложения; χ (ndt) , n=0,1…N-1, – измеренные значения сигнала; X(kdf), n=0,1…N-1, – комплексные амплитуды синусоидальных сигналов, слагающих исходный массив; df – дискретность частоты; dt – дискретность времени.

Фаза сигнала, соответствующего частоте f=kdf, определяется как арктангенс отношения мнимой и действительной части элемента Фурье ряда:

arctg

(ШХ^кй^ ХКеЩкйПУ

Тогда разность фаз сигналов с приемника и излучателя определится по формуле:

(lm(X(kdA\\      / л<р = ar eta I---7— ----^ I - arctq I -

^Ы yRe^kdf^)   "V

Im ^X.^kdf^X

Re^X.Qkdf)))'

что позволяет вычислить время распространения звука в образце твердого тела из выражения (4).

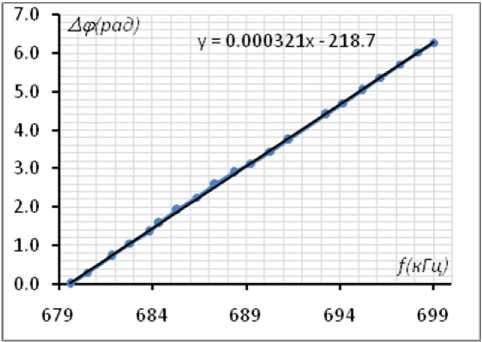
Рис. 3. Зависимость разности фаз гармонических волн на источнике и приемнике ультразвука от частоты

Нами были проведены контрольные измерения в образце твердого тела с известным временем распространения ультразвуковых волн 51,7 µс при t=22 oC, использовался ультразвуковой дефектоскоп Пульсар 1.2.

Из массивов данных, записанных на ПК, нами вычислены разности фаз Δϕ гармонической волны на источнике и приемнике для разных частот f в контрольном образце при комнатной температуре 26 ^оС. Результаты измерений в виде зависимости разности фаз Δϕ от частоты f приведены на рис. 3.

Наклон получившейся прямой вычис-

лен с помощью приложения Excel (рис. 3) и равен 0,000321 рад/Гц. Вычисленное с помощью выражения (4) время распространения ультра- звуковой волны в контрольном образце равно 51,08 µс, при комнатной температуре 26oС. Отсюда можно сделать вывод, что время распространения ультразвука в твердых образцах в импульсном и фазовом методе близки друг другу и в пределах погрешности совпадают с временем в контрольном образце. Обе методики измерения пригодны для дальнейших акустических исследований.