Измерения электрокинетического потенциала частиц биоколлоидов

Исследование граничных потенциалов, определяемых наличием или отсутствием заряженных и/или поляризующихся групп на взаимодействующих поверхностях, имеет длинную историю. Это особенно актуально для водных коллоидных систем, и в частности для систем, содержащих частицы биологического происхождения (например, одиночно живущие бактериальные клетки, частицы физиологических жидкостей или многочисленные модельные частицы, например липосомы размером от малых (0.02 ^ 0.05мкм) до гигантских (5 ^ 100мкм) [1]). Многие фундаментальные параметры таких систем определяются электрическими свойствами воды и водных электролитов [2, 3]. Иногда отмечается [4], что изучение коллоидных дисперсий является способом исследования конденсированного состояния вещества (softmatter).

Поверхностные потенциалы частиц могут быть положительными за счет протонирования или отрицательными при диссоциации поверхностных радикалов. Максимальная плотность связанного отрицательного поверхностного заряда (например, для бислоя на основе фосфатидилсерина), определяющая поверхностный потенциал, оценивается [1] величиной 0.1 ^ 0.2Кл ■ м-2, что соответствует поверхностному заряду микронной частицы, равному примерно 107e. Свободный заряд, определяющий дзета-потенциал, значительно меньше. Мицеллы ПАВ (например, додецилсульфата на- трия) за счет диссоциации катионов Na+ могут нести до 60 элементарных зарядов [4]. Такие электрические параметры поверхностей, как дипольный потенциал мембран, поверхностный потенциал или потенциал двойного электрического слоя, как правило, недоступны прямому измерению. Исключение составляет электрокинетический потенциал (дзета-потенциал), который, хотя также недоступен прямому измерению, может быть вычислен по измеренному значению скорости движения частицы в электрическом поле.

Точность измерения размеров и дзета-потенциалов частиц биологических суспензий имеет и диагностическую ценность, например, при воспалительных и опухолевых заболеваниях легких [5].

Наконец, задача измерения дзета-потенциала актуальна для исследования поверхностей стекол или медицинских полимеров [6], используемых, например, в конструкциях струйных или потоковых микрофлюидных модулей.

МЕТОДЫ ИЗМЕРЕНИЙ

Для измерения параметров частиц дисперсной фазы, т. е. размеров, заряда и электрокинетиче-ского потенциала, могут использоваться принципиально несколько технологий. К ним относятся многочисленные разновидности электрофореза, начиная от кюветы Тизелиуса, электроакустические методы и совокупность новых методов, основанных на измерениях светорассеяния коллоидов.

В клиническом электрофорезе слишком велики дрейфовая длина частиц, что удлиняет время анализа, и соответственно достаточно высокое напряжение (до 1000 В) с целью увеличения напряженности электрического поля. Типичные значения параметров, характеризующие процесс: плотность тока j = 1A ■ м - 2 = 0.1мА ■ см - 2 ; проводимость суспензии с = 0.2 ( Ом ■ м ) ; напряженность электрического поля E = 0.05В ■ см ^{- 1}; дрейфовая (электрическая) подвижность эритроцитов как отношение скорости движения к напряженности электрического поля [7]

ц э = ( 0.87 - 1.35 )( мкм/с )/( В/см ) .

Дзета-потенциал частиц цеолитов субмикронного размера в суспензии на основе дистиллированной воды измерялся с использованием электроакустической технологии на приборе ZetaProbeAnalyzer (Colloidal Dynamic Inc., USA) [8].

Описаны способы [9] использования ультразвука для измерения размеров и электрокинетиче-ского потенциала коллоидных частиц.

Предлагался способ использования электрооптической ячейки [10] для прямого измерения скорости движения предварительно окрашенных частиц в знакопеременном электрическом поле и вычислений электрокинетического потенциала частиц. Для окрашивания использовался анилино-нафталинсульфонат (1,8-АНС). Принципиальный недостаток способа состоял в том, что адсорбция красителя изменяла поверхностный потенциал и заряд частиц, а следовательно, и электрокинети-ческий потенциал.

В последние десятилетия для анализа дисперсного состава, а также и для измерения дзета-потенциалов частиц коллоидов различной природы, включая биомедицинские коллоидные системы, стала широко использоваться совокупность методов динамического рассеяния света (допплеровская спектроскопия, спектроскопия оптического смешения, фотонная корреляционная спектроскопия, спектроскопия квазиупругого светорассеяния, лазерная корреляционная спектроскопия (ЛКС) и другие).

Справедливо считается [11, c. 38–40], что так называемый "оптический пинцет", т. е. воздействие кванта лазерного излучения с длиной волны 500 нм на микронную коллоидную частицу, легко реализуется, тогда как возможность применения в биологической среде "акустического пинцета" частоты 2 МГц (длина волны около 106 нм) гораздо более затруднительна.

Однако в отношении динамического светорассеяния отмечается [12], что "в коммерчески доступных приборах конечный результат не связыва- ется с используемым алгоритмом получения этого результата". В других случаях [4, 5] отмечается, что в методологии ЛКС отсутствуют расчетные соотношения, позволяющие оценить экспериментальные результаты. В целом, несмотря на массовое использование приборов этого типа, преимущества и недостатки методов, основанных на измерениях динамического рассеяния света, описываются недостаточно убедительно. Например, в [13] среди преимуществ отмечаются следующие: небольшое время измерений (от единиц секунд до нескольких минут); широкий диапазон измеряемых размеров частиц (от 0.001 до единиц микрон); коммерческая доступность; крайне малое количество образца (пробы), необходимое для анализа. Считается также, что эта техника абсолютна, т. е. не требует калибровки по известным (эталонным) распределениям.

Среди недостатков отмечаются: низкое разрешение по размерам (1:1000) по сравнению со счетчиками частиц и микроскопией (1:10); отсутствие регулируемых параметров, используемых для калибровки.

Ниже обсуждаются некоторые фундаментальные положения, лежащие в основе метода.

АНАЛИЗ МЕТОДОВ ДИНАМИЧЕСКОГО РАССЕЯНИЯ СВЕТА

Основной эффект светорассеяния состоит в получении допплеровского частотного сдвига, определяемого диффузионными смещениями частиц при воздействии на суспензию монохроматического (лазерного) излучения. Эти частотные сдвиги определяются в первую очередь кинетическими параметрами частиц, т. е. скоростью движения, подвижностью и коэффициентом диффузии, а при наличии электрического поля — зарядом и потенциалом частиц.

Для анализа диффузионных смещений множества рассеивающих свет частиц исторически необходимо было прежде всего записать автокорреляционную функцию положения (координат) частицы, а затем, в соответствии с фундаментальной теоремой Винера—Хинчина—Колмогорова, получить путем фурье-представления спектр рассеянного излучения.

В статистической механике для описания случайных перемещений частиц использовалась (см., например, [14]) автокорреляционная функция вида

( m Y' ^f m (l r |²)

G (r, t )= ----:----    ■ exp--2—~ ,

’ ( 2nt ² k B T J            2 1 ² k B T

V         J выражающая в расчете на единицу объема вероят- ность того, что частица, находящаяся при t = 0 в некоторой точке пространства, спустя промежуток времени t будет найдена в точке, находящейся на расстоянии r от исходной точки. Здесь r

следует понимать как модуль среднего значения трехмерного перемещения частицы. Это выражение для автокорреляционной функции в точности соответствует максвелловскому распределению молекул по скоростям, принятому в молекулярнокинетической теории газов:

f ⁽ V ) =

m I к 2nt2 kB T J

• exp

² mV

2 k b T

к J

тается, что тепловые флуктуации скорости частиц порождают не только допплеровский сдвиг и соответствующие изменения спектра рассеяния, но отражают также и неявно содержащиеся в них значения подвижности, заряда и электрокинетиче-ского потенциала частиц.

Соединение формализма теории тепловых флуктуаций и точных решений в теории рассеяния Ми, которая, как считается [17], для жидких коллоидных взвесей, равно как и для атмосферных коллоидов, дает наилучшие результаты, позволило получить пригодное для практического использования выражение для спектрального распределения рассеянного света в форме лоренцевской кривой [14]:

где V = | ^r|/t — среднее значение модуля скорости частицы.

Фурье-преобразование автокорреляционной функции дает близкое к гауссовскому представление для спектральной плотности рассеянного излучения, т. е.

s (| Ki, а® )=е.

2|K|2 • D

A®2 + K|4 • D2’

S (| K |, A® ) =

m

к 2П K Г k в T J

• exp

m A to ²

\

—

к

2| K |² k в T J’

где K — модуль разности между волновыми векторами падающего и рассеянного излучения; A to — разность круговых частот падающего и рассеянного света, зависящая от скорости движения рассеивающих свет частиц.

Включение в анализ коэффициента диффузии рассеивающих свет частиц с формальной точки зрения эквивалентно замене в последнем выражении, основанной на равенстве A to²/K = D•A®, где D — коэффициент диффузии частиц. Формула Стокса—Эйнштейна D = k _в T[бЕгт) = k _в T • ц_т для коэффициента диффузии определяет механическую подвижность частицы µ m , умножение которой на величину заряда частицы дает электрическую подвижность, а последующее умножение на напряженность поля — значение скорости движения частицы V = Q _p Ц_тE . Отметим здесь, что механическая подвижность частицы определяется только размерами, формой и вязкостью среды, тогда как скорость движения заряженной частицы определяется зарядом частицы и напряженностью электрического поля. Камминс и соавторы в статье [15], считающейся часто исходной для развития в последнее время технических средств [16], предназначенных для дисперсного анализа частиц на основе измерений динамического светорассеяния, не уточняют происхождение, характер и величину напряженности электрического поля. Счи-

где K | • D — диффузионное уширение спектра рассеянного света.

В лазерной корреляционной спектроскопии, широко используемой в биологических исследованиях и в частности в нефелометрическом анализе, для автокорреляционной функции и спектральной плотности используются аналогичные по форме соотношения [18]:

G ( т ) = A exp ( —Г • т ) ,

S(®) = (A •Г/п)/[(to0 — qV)2 +Г2], где A — амплитуда флуктуаций светорассеяния, соответствующая диффузионному уширению Г спектра; т = 1 2Dtq2 — радиус корреляции, т. е. время, в пределах которого поведение частиц статистически независимо; ω0 — частота падающего света; qV — допплеровское смещение частоты падающего света на частицах, перемещающихся в процессе трансляционной диффузии ( q — волновое число; V — скорость частицы). Диффузионное уширение определяется произведением Г = Dt • q2, в котором коэффициент трансляционной диффузии Dt определяется приведенной выше формулой Стокса—Эйнштейна Dt = kвT/блцКh (Rh — гидродинамический радиус частиц). Волновое число q определяется соотношением q = (4пп/Л)sin(0/2), где Л — длина волны падающего лазерного света; n — показатель преломления среды; 0 — угол наблюдения рассеянного света, близкий к π (обратное светорассеяние). Выражение для коэффициента диффузии позволяет вычислить подвижность частиц,

исходя из равенства D t = k _B T • ц, и далее — дзета-потенциал на основе равенства (формула Смолу-ховского) ц = ( 2ss 0 / 3 п ) Z •

Янковский с соавторами [12] методом регуляризации Тихонова (матричное решение некорректных задач линейной алгебры) решали обратную спектральную задачу, которая сводится прежде всего к нахождению функции распределения частиц дисперсной фазы по размерам, а затем может быть использована для нахождения коэффициента диффузии, заряда и электрокинетического потенциала частиц. Авторы отмечают, что "даже при хорошем качестве приборной составляющей аппаратно-программного комплекса", обеспечивающей низкий шум и фон (наличие частот, не принадлежащих спектрам падающего и рассеянного света, например, за счет рассеяния света на молекулах растворителя), достаточно сложно восстановить детали многомодовых распределений частиц по размерам в коллоидных растворах. Особенно это касается сложных биологических растворов (в частности сыворотки крови), содержащих большое количество компонентов. Как отмечают авторы статьи, по этой причине большинство производителей наносайзеров ограничиваются использованием кумулянтов (чаще всего среднего и дисперсии, но также коэффициента асимметрии и эксцесса распределения). Таким образом, удается, по замечанию тех же авторов, надежно описать тривиальное распределение частиц одного размера, либо распределение, состоящее не более чем из двух мод, далеко отстоящих друг от друга. Но уже в более ранних оценках [19] пригодности ЛКС для дисперсного анализа отмечалось, что обработка спектров рассеяния света для полидисперсных систем — обратная задача спектрального анализа с "плохо обусловленной матрицей".

СТАТИСТИЧЕСКАЯ ОЦЕНКА МЕТОДА ДИНАМИЧЕСКОГО СВЕТОРАССЕЯНИЯ

Приведем далее некоторые дополнительные соображения и расчетные выражения для оценки методов светорассеяния. Средний квадрат одномерного электродиффузионного смещения частицы определяется соотношением [20, c. 166–169]

(x - x 0 )2 = Vd212 + 2 Dt , где дрейфовая (электрофоретическая) скорость определяется произведением подвижности и скорости движения частицы Vd = цЕ , а коэффициент диффузии — формулой Стокса—Эйнштейна D = kBT/6nnr. Подвижность, как уже отмечалось выше, определяется соотношением ц = = (4лее0Z/Пт])f (ka), в котором произведение 4KssoZ = Qp определяет заряд частицы; к — дебаевская длина экранирования; a — радиус коллоидной сферы; f (ka) — функция Генри концентрации электролита и радиуса иона. При ka ^ 0 выполняется условие f (ka )^ 1 (предел Хюкке-ля—Онзагера), а при ka ^ да — условие f (ka ) ^ 3/2 (предел Гельмгольца—Смолухов-ского). Во втором случае (f (ka) = 3/2) подвижность дается уже отмеченным выше выражением ц = ( 2sso/3n) Z-

Таким образом, среднеквадратичная скорость электродиффузионного смещения равна

V⁽ x - x 0 ^{) 2} = IV2 + 2D = t                d t

= ( 2SSof f (ka) E )’ + Ik^T

(      3 П     J    6nnrt

Из полученного соотношения непосредственно следует, что диффузионная составляющая скорости определяется временем наблюдения t , тогда как дрейфовая скорость определяется только параметрами среды (вязкость, поляризуемость, напряженность поля) и параметрами движущейся частицы (размер, заряд и дзета-потенциал). Понятно, что для оценки дрейфовой скорости необходимо пренебречь вторым слагаемым под квадратным корнем в правой части выражения, т. е. считать время наблюдения достаточно большим, как это имеет место в практическом электрофорезе.

В практике измерений светорассеяния время измерения, как было отмечено выше, составляет интервал от нескольких секунд до нескольких минут, что само по себе составляет большое преимущество метода по сравнению с электрофорезом. Однако это время не рассматривается как необходимое условие проведения измерительного процесса, а сами измерения непосредственно не связаны с отмеченными параметрами (размер, заряд, электрическая подвижность и электрокине-тический потенциал частиц). Формализм лазерной корреляционной спектроскопии не содержит набора параметров, определяющих электрокинети-ческий потенциал, т. е. характера электролита инкубационной среды, вязкости этой среды, структуры двойного электрического слоя, характера поверхности частиц, включая способность поляризоваться, т. е. именно то свойство, которое определяет рассеяние Ми. Хотя диффузионное уширение спектра рассеянного света, несомненно, отра- жает все свойства коллоидной системы, его затруднительно непосредственно включить в формализм теории Гюи—Чапмена—Штерна. Отсюда понятно замечание Янковского и соавторов [12], отмеченное выше, что результат измерения не связан с алгоритмом получения этого результата.

Уже достаточно давно для аэродисперсных коллоидов (аэрозолей) было показано [20, c. 166– 169], что ошибка при определении размера частиц по броуновскому движению может быть в десятки раз больше, чем по скорости направленного движения (например, седиментации), и лишь для очень мелких частиц (< 0.1 мкм) броуновские флуктуации скорости могут быть использованы для оценки размеров частиц. Ошибка оказывалась еще больше при измерениях скорости движения заряженных частиц в сильном электрическом поле. Эти выводы очевидны, поскольку для малых частиц скорость таких флуктуаций становится значительно больше скорости упорядоченного движения и быстро возрастает с уменьшением размеров.

Можно полагать, что для жидкостных коллоидов такие ошибки еще больше, поскольку броуновские смещения частиц гораздо меньше и, следовательно, более трудно измеримы.

Недифузионный характер движения при очень малых временах не только газовых молекул, но и рассеивающих свет коллоидных частиц стал интересен уже сравнительно давно [21]. Совсем недавно баллистическое (неброуновское) движение одиночной частицы в наносекундном временнόм интервале непосредственно наблюдалось впервые, как утверждают авторы статьи [22], в оптической ловушке с полосой пропускания 75 МГц. При этих исследованиях положение частицы измерялось с точностью в единицы ангстрем.

В целом измерения светорассеяния, как и лежащие в его основе диффузионные перемещения рассеивающих свет частиц, имеют статистическую природу и в любом случае дают усредненные результаты, тогда как размер, заряд, дзета-потенциал и другие детерминированные параметры частиц определенного сорта могут быть в принципе точно измерены.

ПРЕДЛАГАЕМЫЙ МЕТОД ИЗМЕРЕНИЯ

В этой статье рассматривается способ, родственный электрофорезу, измерения размеров частиц и электрокинетического потенциала на основе непосредственного измерения скорости частиц в электрическом поле.

Используем в качестве основного параметра частиц время кинетической релаксации, характеризующее длительность установления стационарного движения частицы в вязкой среде при действии электрической силы. Для заряженной частицы, несущей электрический заряд Q p , установившаяся скорость дрейфа V_d = цЕ ( ц — подвижность частицы) в электрическом поле напряженности E дается соотношением Стокса ^{6 n r n} V₄ = Q p Е , не содержащем, однако, время в явном виде. Поскольку кинетические параметры не зависят от характера действующей на частицы силы, время кинетической релаксации τ _k можно определить, если воспользоваться механическими аналогиями цЕ ^ дт и Q p ^Е ^ mg , в которых gτ и mg означают соответственно скорость седиментации и вес частицы, имеющей плотность ρ . Тогда время кинетической релаксации определится формулой т _k = ( 2 r² р/9п ) , общеупотребительной в механике аэрозолей. Например, для частицы радиуса r = 1 мкм, плотностью р = = 10 3 кг • м ^{- 3} (вода), движущейся в среде с вязкостью п = 10 ^{- 3}Па • с (вода), это время равно т _k = = 0.2^мкс. Произведение l j = V • т k определяет инерционный пробег частицы после окончания действия электрической силы. Для микронной частицы, имеющей дзета-потенциал Z = 30 мВ и заряд Q p = 2000 e , движущейся в электрическом поле напряженности Е = 2 В • см ^{- 1} со скоростью около V = 3 мкм • с ^{- 1} инерционный пробег составляет не более 0.01 Å .

Отметим также, что дебаевское время релаксации т _d = 4 пп*a³ /к _B T , характеризующее скорость поляризации частицы, определяется формулой Дебая т _d = 4пп * a³ /к _B T , в которой п * — микровязкость дисперсионной среды, a — радиус сферической дипольной молекулы. Показано экспериментально, что дебаевское время релаксации (10 ^{- 12} ^ 10 ^{- 9} с) существенно меньше времени кинетической релаксации и, кроме того, определяется макроскопическим значением вязкости [23]. Ниже описаны элементы установки, предназначенной для реализации способа и методики измерений.

Для измерений использовалась дифференциальная кювета, содержащая два близко расположенных цилиндрических канала, диаметр и длина которых были равны соответственно d _k = 7 мм; l _k = 40 мм. Оба канала заполнялись

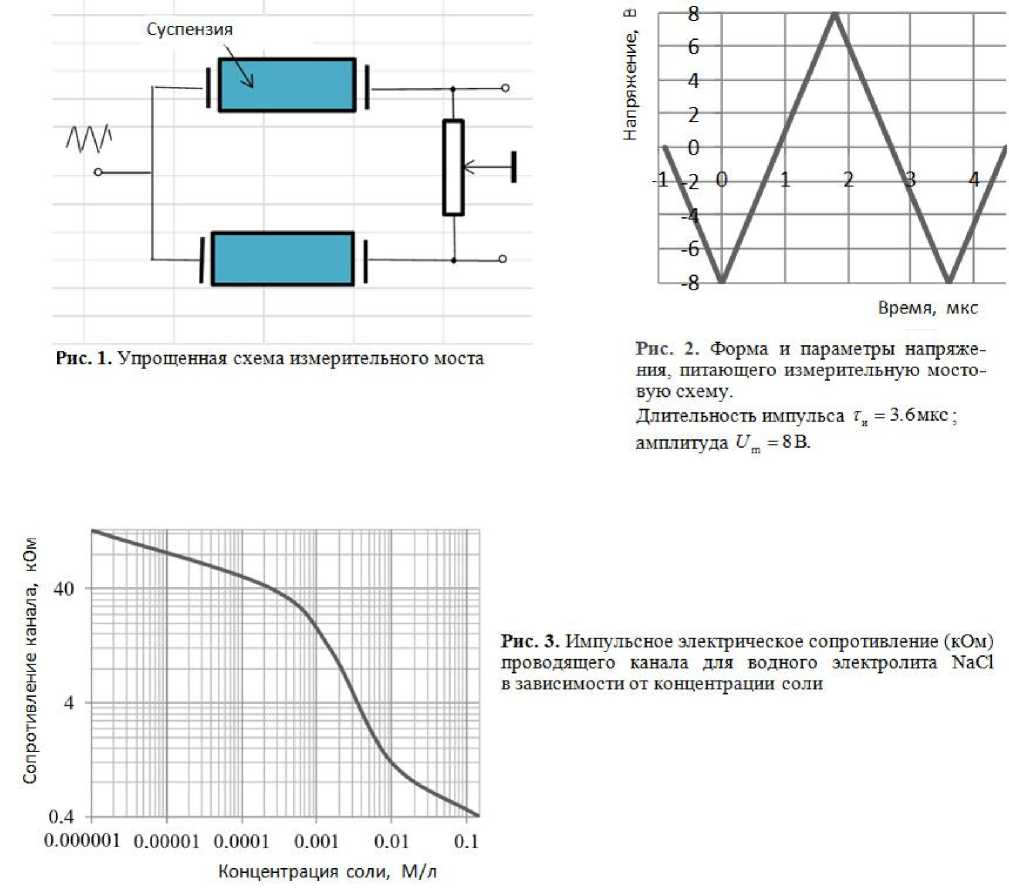
электролитом ( NaCl ) и включались в качестве двух смежных плечей в измерительный мост, схема которого представлена на рис. 1. Мост питался импульсным напряжением, форма и параметры которого показаны на рис. 2.

Два других смежных плеча представляют собой низкоомный потенциометр (50 Ом) с заземленной средней точкой, использовавшийся для балансировки моста. Практически балансировка моста могла быть выполнена с точностью до напряжения не более 1мВ, измеренного в диагонали моста. Зависимость электрического сопротивления (импеданса) канала от концентрации NaCl приведена на рис. 3. Верхняя граница концентрации

(0.15М • л 1 ) соответствует физиологическому раствору и наименьшему сопротивлению канала; нижняя граница примерно соответствует дистиллированной воде; длительность импульса т _и = 3.6мкс ; амплитуда импульса U m = 8В. Диаметр и длина канала соответственно d _k = 7 мм; l _k = 40 мм.

Таким образом, небольшое сопротивление уравновешивающего мост потенциометра позволяет хорошо выполнить балансировку даже при наименьшем сопротивлении канала (физиологический раствор). После уравновешивания в один из каналов добавлялась исследуемая суспензия (рис. 1).

В питающую диагональ моста подавалось линейно изменяющееся напряжение U (t ) = к и • t, представляющее собой антипериодическую функцию времени U (t + T]^)^ = —U (t) амплитуды Um = 8 В и периода T = ти с коэффициентом пропорциональности, равным ки = Um /(ти /4). Форма и параметры питающего напряжения показаны на рис. 2. Фурье-спектр такого сигнала отображается суммой f (t ) = U f(—1) “sn^TO

^{J (}) n ² t f ⁽ )       к²

( к = 1,3,5,...; го = 2 п[T )

и содержит знакопеременные нечетные sin-гармоники, быстро уменьшающиеся по амплитуде (в отношениях 6.48 : 0.72 : 0.26 : 0.13 : 0.08 и т. д.). Для сравнения отметим, что для меандра с фурье-спектром sin kωt k

”, f ( • ) = —z п к = 1

( к = 1,3,5,...; го = 2 п/T )

содержание высших гармоник существенно выше. Генератор питающего напряжения U _пит. представлял собой самовозбуждающуюся петлевую схему, содержащую последовательно соединенные регенеративный элемент (триггер Шмитта) и интегратор, выполненные на основе высокоскоростных ( V_u >  50В / мкс) операционных усилителей.

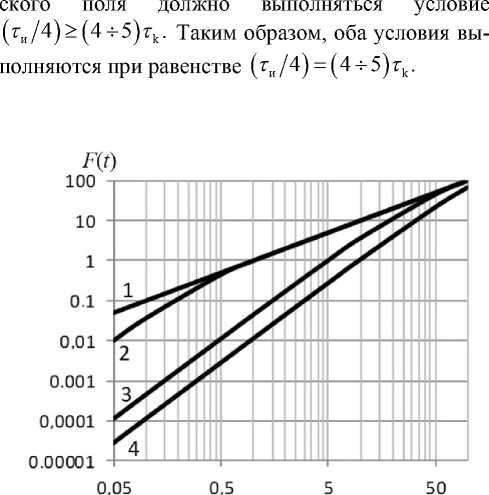
Инерционное торможение заряженной частицы и реальная скорость ее перемещения при импульсном воздействии U (t) = ки • t электрического поля определяются зависящим от времени экспоненциальным множителем р — exp (—t/тk )], так что начальная скорость движения при t = 0 (скачок напряженности поля при перемене полярности) равна нулю, а разложение в степенной ряд при малых временах (t« тk) дает почти линейное возрастание скорости. Множитель р — exp (—t/тk)], получающийся путем интегрирования экспоненты exp (—t/тk), является общим для многих процессов. Произведение F(t) = t |j — exp(—tlтk)] определяет запаздывающий по времени отклик системы (движущейся в электрическом поле частицы), т. е. эквивалентно автокорреляционной функции (свертке), зависящей от времени напряженности поля, определяющей реальную скорость движения частицы. Нетрудно подсчитать, что при заданной (как отношение разности потенциалов к длине канала) напряженности поля для достижения стационарной скорости требуется промежуток времени (4 ^5)тk. Таким образом, треугольный импульс длительностью ти = 1.8мкс (рис. 2) следует рассматривать как оптимальный для частиц радиуса r ^ 1.5мкм. На рис. 4 показаны автокорреляционные функции в зависимости от радиуса частиц. Из этого рисунка, в частности, следует, что для исследования микронных частиц длительность импульса электрического поля должна быть не менее 1мкс , а для десятимикронных частиц — не менее 100мкс . Рис. 4 показывает также, что хорошее разрешение для относительно крупных частиц (1– 20 мкм) получается на временнόм отрезке менее 100мкс, а для субмикронных частиц (0.1– 1 мкм) — на отрезке, не превышающем 1мкс. Немного ниже показано, что для усреднения (необходимого для расчетов) напряженности электриче-

Время?, мкс

Рис. 4 Зависимость автокорреляционной функции F(z) = r[¹-exp(-r/T_fc)] для частиц различного радиуса г.

1 — г =0.1мкм(г_к = 2.2 -КГ³ мкс),

2 — г = 1мкм(г_к = 0.22мкс),

3 — г = 10мкм(гк = 22мкс),

4 — г = 20мкм(т_к = 88мкс)

Колебательное движение частицы определяется знаком питающего напряжения (рис. 2). В течение положительного полупериода напряженность поля и скорость частицы возрастают сначала от нуля до максимального значения, после чего падают и при выполнении условия ( т и/ 4 ) > ( 4 + 5 ) т к становятся нулевыми к началу отрицательного полупериода. Далее точно так же начинается ускоренное движение в обратном направлении.

Для оценки средних значений разности потенциалов и соответственно напряженности поля достаточно выполнить интегрирование для половины (0 <  t <  т _и /4 ) положительного полупериода питающего напряжения:

U пит. = ( 7^ 4 ) 2^ "^ t ^ - exp ^{( -} t* ^Т и ^^d t "

Результат интегрирования записывается в виде

U

ср. пит.

= U m

-^ k- I l т и/4 ^J

1 - e -^{т т k} l

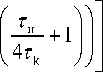
Это выражение показывает, что при возрастании длительности импульса усредненное напряжение монотонно приближается к предсказуемому уровню ( 12 ) от максимального. В таблице приводятся значения усредняющего коэффициента в зависимости от отношения τ _и τ _k и погрешности усреднения в процентах.

Из таблицы следует, например, что при действии короткого импульса на относительно тяжелую частицу ( т _и = 0.5 т _к ) эффективная напряженность поля мала (0.04 от среднего), а вклад частиц этого сорта в электрофоретический ток также мал и может быть сделан еще меньше. Эти соображения становятся важными при анализе полидисперсных коллоидов.

Таким образом, установившееся движение частицы заданного времени релаксации т _k ( r ) в электрическом поле постоянной (усредненной) напряженности соответствует условию ( ^т и/² ) > > ( 4 ^ 5 ) т _k. Отметим еще раз, что для сохранения

хорошей разрешающей способности это условие должно сопоставляться с противоположным по смыслу условием ( т и/ 2 ) < ( 4 + 5 ) т к и соответственно с вытекающим отсюда равенством ( ^т и/² ) = ( ⁴ ^ ⁵ ) ^т к . Это условие непосредственно просматривается на рис. 4.

Порядок измерения и расчетов электрокинети-ческого потенциала для наиболее простого случая монодисперсного коллоидного раствора сводится к следующему. После балансировки моста и добавления исследуемой суспензии ненулевая разность потенциалов в измерительной диагонали моста U _д определяется только электрофоретическим током частиц ^I эф , протекающим в соответствующем плече балансировочного резистора R ₀ . Этот ток определяется соотношением ¹ эф U . /( R 0/ 2 ) , а соответствующая плотность тока — соотношением j эф = ^{2 U} д /( R . S к ) ( S _к — площадь поперечного сечения канала). Далее из формулы (закон Ома в дифференциальной форме) j _э ф = ^а к " E ( E = U _пит / ^ к — напряженность электрического поля в канале) следует найти проводимость канала ^ к = ^{2 U} д " l к /( R e " S к " U пит. ) .

Плотность электрофоретического тока, используя заряд одиночной частицы Q _p и концентрацию заряженных частиц n , можно определить также на основании равенства j эф = Q _p • n • Ц э • E , где произведение ц э • E дает скорость движения частицы, а произведение Q _p • n — объемную плотность заряда движущихся частиц. Равенство

^{2 U} д • l к

R . • S к • U пит.

= z2 [4я(ее0)2 • r • n •(In)

позволяет рассчитать для монодисперсного коллоидного раствора с известным радиусом частиц значение электрокинетического потенциала:

z =

2 U д l к η

l ^{4 п} ( ^ее 0 ) ² R 0 ^S к ^U пит. rn ,

Значения усредняющего коэффициента и погрешности усреднения в зависимости от нормированной длительности электрического импульса

τ и τ k	0.5	1	2	4	8	16	24	32	40
Коэф. уср.	0.040	0.076	0.139	0.236	0.351	0.443	0.473	0.484	0.490
Погр. уср., %	96.0	92.4	36.1	26.4	14.9	5.7	2.7	1.6	1.0

Для совокупности параметров lк,η,ε,ε0, R0, Sк,Uпит. целесообразно ввести, используя принятые выше обозначения, коэффициент пропорциональности kz = 21кП4п(880 )2 RoSкUпит. [в/м2 ] .

Еще три параметра, т. е. измеренная разность потенциалов U _д , известные значения радиуса частицы r и объемной концентрации частиц n , определяют множитель U _д ( Гrn ) , имеющий размерность ^[ В • м² ] . Таким образом, формула для расчета электрокинетического потенциала частицы приобретает вид

Z = 4k z ■ U ,/( r • n ) .

Анализ полидисперсных коллоидов, в особенности в тех случаях, когда составляющие фракции имеют близкие размеры, как всегда, представляет существенные трудности. Технически наиболее просто использовать изложенные выше методы и расчеты для нескольких последовательных (проводимых одновременно) измерений, увеличивая дискретными ступенями период следования и соответственно длительность импульса питающего напряжения. Границы этих ступеней должны перекрываться. Число ступеней, равно как и интервалы дискретизации, определяются фракционной структурой коллоида, если она известна, или принимаются равными. Увеличение электрофоретического тока на каждом шаге этого процесса определяется взвешенными вкладами всех составляющих коллоида, причем эти вклады, как отмечено выше, могут быть оценены заранее. Кроме того, для придания измерительной системе свойства адаптивности при увеличении тока должен уменьшаться интервал дискретизации, причем тем больше, чем быстрее возрастает ток. Для алгоритмизации процесса целесообразно использовать такие корреляционные методы, как "частичное перекрытие — сложение" (overlap-add) [24], используемые в самых разных приложениях, например для измерения радиосигналов на фоне шумов или для распознавания сигналов в нервных сетях.