Измеритель концентрации подвижных микроорганизмов в макро- и микрообъемах

Измерение концентрации подвижных инфузорий является актуальной задачей для решения экологических и медицинских задач. В экологических исследованиях по уменьшению доли концентрации подвижных организмов можно оценивать токсичность химических веществ и смесей. В медицинских исследованиях аналогичные измерения проводятся для исследования эндотоксикоза путем определения токсичности сыворотки крови. О степени токсичности судят по уменьшению за определенное время концентрации живых (подвижных) инфузорий на 50 % или в общем случае на X %. Если оценку токсичности водных сред возможно проводить в больших кюветах, то токсичность сыворотки крови желательно исследовать в микрообъемах (минимальный забор крови у пациента).

Обычно число живых инфузорий измерялось методами микроскопного счета в каплях среды. Однако это очень трудоемкий и длительный способ. При создании прибора, позволяющего производить измерения концентрации таких инфузорий в макро- и микрообъемах проб, необходимо разработать модель измерительного преобразователя (ИП). Физико-математическая модель ИП является развитием модели, описанной в [1].

ЗАДАЧА ПОСТРОЕНИЯ ИЗМЕРИТЕЛЯ КОНЦЕНТРАЦИИ ИНФУЗОРИЙ

В МАКРООБЪЕМАХ

Оптическая модель популяции инфузорий может быть описана равномерной взвесью рассеивающих сфер с радиусом r и коэффициентом дифракции р = 2 лг/X >  100 , где X — длина волны падающего света. Расстояние между клетками много больше размеров частиц. Этологические (поведенческие) особенности движения инфузорий характеризуются прямолинейными перемещениями ("пробегами") под случайным углом на расстояние £ с частотой смены направлений V .

Моменты изменения направлений движения образуют случайный поток. Будем полагать, что случайный поток — пуассоновский. Возможным обоснованием этого предположения может быть то, что изменение направления есть результат суммирования случайных информационных потоков, воспринимаемых множеством сенсоров-ресничек, расположенных по периметру инфузории. В экспериментах наблюдалось (например, при воздействии некоторых антибиотиков), что частота смены направлений и длина "пробега" взаимосвязаны. Иными словами, инфузории могут перемещаться или, редко меняя направления, длинными "пробегами", либо, часто меняя направления, короткими "пробегами".

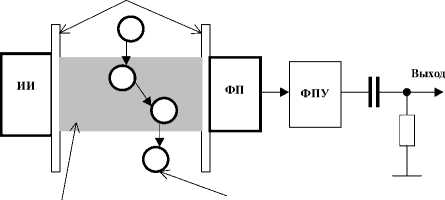
Для обнаружения движущихся инфузорий предлагается физико-математическая модель измерителя подвижных биологических объектов. Движущиеся частицы находятся в объеме оптического ИП между источником излучения (ИИ) (монохроматическим, коллимированным) и фотоприемником (ФП) (рис. 1, а). Подвижные рассеивающие частицы с р >  100 , движущиеся в освещенном объеме, создают ореол рассеяния на ФП. Из работ Шифрина К. С. [2] известно, что суммарная интенсивность света на фотоприемнике от такой движущейся частицы (например, капли дождя) не меняется при движении частицы в потоке излучения вдоль и поперек. Поэтому, пока частицы находятся внутри освещенного объема, суммарная освещенность ФП не меняется (справедливо для случая малой концентрации частиц). Ее изменение возникает при выходе частиц из контролируемого фотоприемником объема или вхождении их внутрь (рис. 1, а). Если фиксировать изменения сигнала ФП, то появляется возможность счета подвижных биологических частиц в результате образования случайного потока импульсов. Пусть концентрация частиц в единице объема равна C . Поток возникает за счет движения частиц из приграничного слоя, толщиной не превышающего среднюю величину £ "пробега" инфузорий (рис. 1, б). Интенсивность потока зависит от концентрации частиц в объеме:

а

Стенки кюветы

Контролируемый объем              Частица

(в луче света)

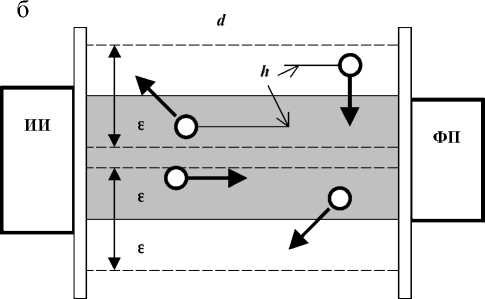
Рис. 1. Оптический ИП для измерения концентрации подвижных инфузорий (а) и поток частиц через границы контролируемого им объема (б).

ИИ — источник излучения, ФП — фотоприемник, ФПУ — фотопреобразующий усилитель, h — величина расстояния частицы до границ контроля ИП, £ — толщина приграничных слоев

Л = 2 ■ C ■ L ■ £ ■ v ■ d ■ p , (1)

где L — периметр ФП; d — расстояние между ИИ и ФП; £ и v — параметры движения инфузорий, которые обсуждались ранее; p — вероятность для частиц пересечения границы освещенного объема при изменении направления.

Расчет вероятности p основан на следующих предположениях: а) частица находится на случайном расстоянии h от границы ( h <  £ ); б) частица перемещается скачком под случайным углом на расстояние £ . Расчет вероятности p аналогичен задаче Бюффона, т. к. "тень" частицы проецируется на поверхность ФП. Для расчета интенсивности Л важна не величина вероятности, а ее равенство для всех частиц. Так как £ и v взаимосвязаны, то:

Л = K ■ C, (2)

где K — коэффициент, зависящий от конструкции ИП и вида микроорганизма.

Число частиц, пересекающих границу ИП за время Т,

N = Л^ T .                 (3)

В данном случае полагаем, что объем кюветы с частицами много больше контролируемого объема, т. е. в опытах используется большое число частиц (взвесь с концентрацией С).

ЗАДАЧА МАКСИМИЗАЦИИ ИНТЕНСИВНОСТИ ПОТОКА ЧАСТИЦ ДЛЯ СЛУЧАЯ МАЛОГО ИХ ЧИСЛА

Если измеряется концентрация частиц в микрообъемах сыворотки крови, то необходимо учитывать конечность числа частиц в объеме. Тогда одни и те же частицы могут снова изменять направление при соприкосновении со стенками кюветы (такой эффект случайного "отражения" наблюдается при экспериментальных исследованиях) и многократно повторно пересекать границы контролируемого объема ИП. Суммарный однородный поток с независимым приращением "отражений" также будет иметь пуассоновский характер. Важно, что эти свойства обусловливают эргодичность траекторий частиц (то есть одинаковую плотность), что позволяет измерять интенсивность потока в любом месте контролируемого объема.

Даже в случае нарушения условий случайности "отражения" частиц от границы в суммарном потоке с независимыми приращениями возможно выделить пуассоновский поток, т. к., согласно теореме Леви, каждый процесс с независимыми приращениями является суммой трех независимых процессов (которые не обязательно все присутствуют): детерминированного (центрующего), с независимыми приращениями со скачками в фиксированные моменты времени, стохастически непрерывного с независимыми приращениями [3].

Непрерывная часть любого процесса с независимыми приращениями есть либо гауссовский процесс с независимыми приращениями, либо пуассоновский, либо их сумма. Поэтому в случае движения частиц пуассоновский поток с независимыми приращениями со скачками в фиксированные моменты времени по Леви будет обязательно присутствовать.

При построении модели будем считать постоянной не концентрацию С , а число частиц п. Тогда концентрация

^C =^.               ⁽⁴⁾

общ.

Здесь V общ — общий объем взвеси в ИП.

Если объем приграничных слоев (рис. 1, б):

V пр = 2 • L • е • d , тогда интенсивность потока частиц в ИП, согласно формуле (1),

Л ип = — V пр< v • p .          (5)

^V общ.

Следовательно, интенсивность потока определяется долей числа частиц приграничных слоев от общего числа частиц в контролируемом объеме.

Рассмотрим возможности максимизации интенсивности потока.

Увеличение относительной величины приграничного объема

V _пр

Для увеличения соотношения    р.  до ≈ 1

^V общ.

площадь ФП должна быть сравнима с площадью бокового сечения кюветы (рис. 2). Если ФП имеет форму круга радиусом a (рис. 3), то

^S фп = ^п • a , L фп = ² • ^п • a , V _пр. = 4 • п • d • a • е .

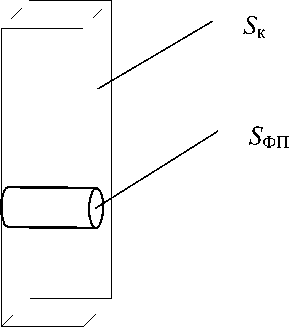
Рис. 2. Соотношение площади ФП с площадью стенки кюветы. S _к –— площадь грани кюветы, S ФП — площадь фотоприемника

Площадь внутреннего сечения ИП и его внутренний объем

Sип = п(a + е)2, Vобщ. = п • d(а + е)2.    (7)

Концентрация частиц в этом объеме

C =---Г--v • п • d ( а + е )²

Увеличение вероятности пересечения границы ИП инфузориями

Максимизация потока за счет увеличения p возможна, если поток отражается от границ и создает дополнительные независимые приращения. Интенсивность потока для ИП c учетом (6–8)

Л ИП =

4 • n • п • а • е • d d • п(а + е)2

(v • Р) •

Определим, при каком соотношении а и е интенсивность потока будет максимальна. Пусть а = к • е . Тогда

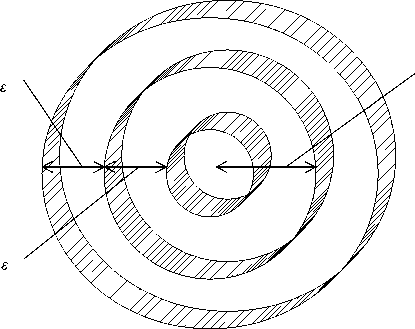
Рис. 3. Вариант ФП.

а — радиус ФП, е — толщина приграничных слоев

Л ИП = 4 • n •v • Р

к

Ц к + 1) 2)

Значение Л _ИП будет максимально при к = 1, т. е.

а = е .

ИП для микрообъема может иметь, например, форму капилляра. В таком случае отношение интенсивности потока в ИП к интенсивности потока во всем объеме кюветы Λ К при одних и тех же значениях S _ФП , n , d и а = е

^Л ИП

Л к

n

V К общ.

У пр.

• v • p

S к

n

Vпр. Р об.к

⁴ • ^S ФП

Здесь V _{g6 к} = S _к • d , где S _к — площадь грани кюветы (рис. 2), которая заполнена инфузориями, d — толщина кюветы.

Так, если площадь грани стандартной фотометрической кюветы S к ≈ 5 cм², а S ФП ≈ 4 мм² (например, для фотодиода ФД-256), то выигрыш по потоку при использовании ИП в виде капилляра может достигать 30 раз.

Оценка интенсивности потока событий может проводиться согласно алгоритмам, приведенным, например, в работе [4].

ВЫВОДЫ

• 1.    В статье описана физико-математическая модель измерителя концентрации подвижных инфузорий, основанная на этологических (поведенческих) и оптических свойствах данных микроорганизмов.

• 2.    Предложен ИП, позволяющий измерять концентрацию инфузорий в микрообъемах и обоснованы его основные характеристики.