Изображающие системы на основе обобщённых линз

Классическая изображающая оптическая система состоит из сферических линз и зеркал. Так исторически сложилось по причине простоты технологии формирования сферической поверхности, которая реализуется на очень простом оборудовании с несложным набором технологических операций, который не сильно изменился за последние сотни лет развития оптического приборостроения. Оптические изображающие системы на основе асферических линз намного компактнее и проще в конструкции, поскольку содержат меньше элементов. Однако технологии их изготовления намного сложнее технологий изготовления сферических линз, поэтому широкое использование асферических линз в массово выпускаемых изображающих системах началось относительно недавно (последние 20 лет). Основные типы асферических поверхностей для линз, которые используются в настоящий момент, описаны в [1].

Схема использования асферических линз в изображающих оптических системах довольно стандартная: в объективе группа сферических линз заменяется на один асферический элемент, который проводит исправление волнового фронта, формируя практически идеальный гомоцентрический пучок. Обычно используется что-то из стандартного набора асферических линз [1]. Под асферической линзой можно понимать гораздо более широкий класс элементов, в том числе и осесимметричные элементы свободной формы. Одним из таких элементов является обобщённая линза [2]. Обобщённая линза подробно описана в работах [3, 4], однако, как следует из этих работ, получение изображения с помощью одиночной обобщённой линзы или невозможно, или получается изображение плохого качества.

Если в оптической системе несколько элементов, всегда можно подобрать фазовую функцию одного из элементов таким образом, чтобы на выходе оптической системы формировался гомоцентрический пучок. Развитие технологий формирования микрорельефов с высотой существенно больше микрометра даёт возможность изготовления дифракционных [5, 6] или гармонических линз [7], аппроксимирующих любую асферическую поверхность [8]. Конечно, в этом случае необходимо компенсировать хроматические искажения [8, 9], но с увеличением высоты рельефа они уменьшаются [7]. Трудоёмкость этой технологии не зависит от формы поверхности, которая аппроксимируется микрорельефом. По сравнению с рефракционной линзой плоский микрорельеф обладает заметным преимуществом – габаритами. Толщина таких линз, даже с учётом толщины подложки, существенно меньше толщины рефракционных линз. Существенно меньше и ограничение на расстояние между отдельными гармоническими линзами. Его можно уменьшать практически до нуля в процессе расчёта и оптимизации оптической системы. В результате система из гармонических линз может быть существенно компактнее рефракционного объектива.

Оптические свойства дифракционных и дифракционно-рефракционных систем для задач формирования изображений хорошо описаны в [8–15].

Использование асферических линз со свободной формой поверхности даёт дополнительную степень свободы при проектировании многолинзовых объективов. Разработчики освобождаются от ограничений на форму используемых асферических линз. Возможно использование в таких системах элементов, которые в отдельности не являются изображающими. Вследствие этого практически нет ограничения на траекторию лучей в оптической системе, что потенциально может позволить получить большую светосилу оптической системы при существенно меньшей длине оптической системы. Отклонение от гомоцентрично- сти пучка в такой системе может компенсироваться всего одной асферической обобщённой линзой.

В рамках этой работы не будут рассматриваться компактные системы, не ставится в качестве цели рассмотрение использования гармонических линз, поскольку моделирование ведётся в приближении тонкого элемента для одной длины волны. В работе рассматривается метод компенсации негомоцентрич-ности фокусируемого пучка за счёт использования компенсирующей обобщённой линзы, а именно: рассматривается афокальная система – аналог телескопической системы, как наиболее простой для моделирования, где вместо параболических линз установлены обобщённые линзы.

E 2 ( x , y , z ) =

/    -1 X +да +да l-^-II JE1(x',y')■ e

2 n z

-да -да

' d x 'd y ',

где E 1 ( x' , y' ) – комплексная амплитуда светового поля после первой линзы.

Фазовая функция второй линзы определялась простым способом: на вход системы подавалась плоская волна, далее согласно (3) вычислялась комплексная амплитуда светового поля перед второй линзой системы. Фазовая функция линзы определялась по формуле

Ф ( r ) = 2n- arg [ E 2 ( x , y , z ) ] .

1. Обобщённая линза

В работе будем рассматривать обобщённую параболическую линзу как оптический элемент, функция пропускания которого определяется формулой:

T ( r ) = exp ( - iCr m ) ,

где c – масштабный множитель, m – степень обобщённой линзы, r – координата радиус-вектора линзы. Надо понимать, что такая линза, за исключением случая m =2, не будет изображающей, но есть возможность получения чёткого изображения в системе из двух линз. Для этого надо подобрать фазовую функцию второй линзы, которая полностью компенсирует негомоцентричность пучка, сформированного первой линзой. Будем называть обобщённой линзой линзу с функцией пропускания:

На выходе системы получается плоский волновой фронт, следовательно, система преобразует плоскую волну в плоскую волну и является аналогом Фурье-коррелятора для обычных линз. Однако, в отличие от классического Фурье-коррелятора, у этой системы есть некоторые отличия. Например, отсутствует частотная плоскость, а вместо неё есть множество частотных плоскостей, расположенных на отрезке от f 1 до f 2 . Полная математическая модель системы представляет собой три преобразования Френеля.

E ( x , У ) = exp ( iCr m ) l - -— |x к 2ns i )

+да +да x f f E0 (x,y)exp 1-^—Г(x

2 s

-да -да                                 ¹

- x ‘ ) 2 + ( y + y ‘ ) 2 1 d x ‘ d y ‘

T ( r ) = exp [ i Ф ( r ) ] ,

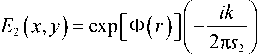
где Ф( r ) – произвольная функция.

На рис. 1 показана схема работы системы.

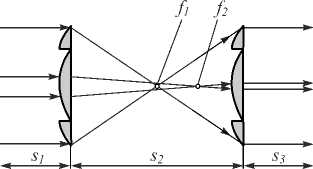
Рис. 1. Афокальная система из двух обобщённых линз: f 1 – минимальное фокусное расстояние, f 2 – максимальное фокусное расстояние, s 1 – расстояние от входной плоскости до первой линзы, s 2 – расстояние между линзами, s 3 – расстояние от второй линзы до выходной плоскости

⁺да⁺да     , . r ik r.

^x J J E i ( x , y ) exp I ^- 27 [ ( ^x

-да -да                      I ²

- x ‘ ) 2 + ( y + y ‘ ) 2 1 d x ‘ d y ‘

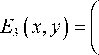
+да +да

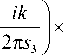
xJJ

-да -да

E 2 ( x , y ) exp

-

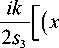
- x ‘ ) 2 + ( y + y ‘ ) 2 1 d x ‘ d y ‘

Функция Ф( r ) второй линзы подбирается, исходя из условия формирования плоского волнового фронта на выходе системы.

2. Математическая модель

Формирование интенсивности на выходе оптической системы, состоящей из 2 обобщённых линз, рассматривалось в параксиальном случае. Для моделирования распространения света использовалось преобразование Френеля. Таким образом, комплексная амплитуда перед второй линзой определяется следующим образом:

где E 0 ( x , y ) – комплексная амплитуда во входной плоскости, E 1 ( x , y ) – комплексная амплитуда после первой линзы, E 2 ( x , y ) – комплексная амплитуда после второй линзы, E 3 ( x , y ) – комплексная амплитуда в выходной плоскости.

В отличие от классического Фурье-коррелятора, расстояние между линзами можно менять в широких пределах. Минимальное расстояние не может быть меньше f 2 – максимального фокусного расстояния первой линзы, а максимальное расстояние может быть определено, исходя из условия работы системы без потерь, т.е. весь свет, преобразованный первой линзой, должен попасть на вторую линзу.

Расстояние s 3 определялось вычислительным экспериментом, в ходе которого прямым перебором определялась плоскость с наименьшим размером изображения точечного светящегося объекта во входной плоскости.

3. Вычислительный эксперимент

Для проведения вычислительного эксперимента была использована параболическая обобщённая линза с m =2,1 (рис. 2 а ) диаметром 50 мм. Моделирование проводилось для длины волны 532 нм. Использовались изображения, размер которых составлял 512×512 отсчётов. Несмотря на то, что показатель степени обобщённой параболической линзы не сильно отличается от двойки, изображение линза строит крайне плохо. На рис. 2 б показано распределение интенсивности вдоль оптической оси линзы. Видно, что фокальный отрезок по длине составляет примерно 0,2 от фокусного расстояния f 1 = 1,45 м, f 2 = 1,8 м. Для исходной параболической линзы ( m =2) фокусное расстояние составляло 1,5 м. На рис. 2 в сформированное такой линзой изображение.

Рис. 3. Фазовая функция обобщённой линзы для установки в афокальную систему вместе с линзой, фазовая функция которой представлена на рис. 2а

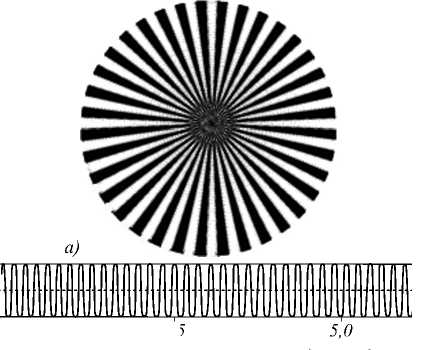
Представим результаты моделирования формирования изображений в такой оптической системе. Для сравнения аналогичное моделирование производилось для системы из двух параболических линз с m =2, т.е. для классического Фурье-коррелятора. В качестве тестового изображения была взята радиальная светотехническая таблица (рис. 4), которая обычно используется для испытания объективов. Физический размер изображения составил 2 мм.

Интенсивность, 'Ю4

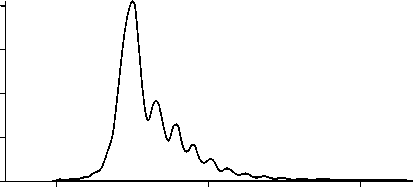
Рис. 4. Изображение радиальной светотехнической таблицы на входе оптической системы

б)

1,4                  1,7                  2,0

После прохождения через оптическую систему, состоящую из 2 параболических линз с m =2, на выходе получается распределение светового поля, которое представлено на рис. 5 а . Для оценки качества формирования изображения была использована ча-

стотно-контрастная характеристика, которая определялась по формуле

k =

^I max

^^^^^^в

^I min

I max + I min

в)

Рис. 2. Фазовая функция параболической обобщённой линзы с m=2,1 (а), распределение интенсивности вдоль оси распространения при падении на линзу плоской волны (б), изображение светотехнической таблицы на расстоянии 1,55 м от линзы (в)

Фазовая функция корректирующей линзы была рассчитана для расположения второй линзы на расстоянии f 2 от первой на основе формулы (4).

Фазовая функция корректирующей линзы представлена на рис. 3.

где I max – средняя яркость светлых полос в сечении изображения, I min – средняя яркость темных полос в сечении изображения. На рис. 5 б , в , г представлены сечения изображения рис. 5 а по разным радиусам. Так, для рис. 5 б был использован радиус 0,95 мм, для рис. 5 в – 0,5 мм, а для рис. 5 г – 0,3 мм. На основе обработки получившихся сечений по формуле (1) была рассчитана частотно-контрастная характеристика для оптической системы. График зависимости контраста от частоты представлен на рис. 5 д .

Как видно из графика, частотно-контрастная характеристика системы близка к таковой в дифракционноограниченном случае. Действительно, при диаметре 50 мм и фокусном расстоянии 1500 мм диаметр пятна

На рис. 6 б – частотно-контрастная характеристика, соответствующая рис. 6 а . В целом, отличий не-

рассеяния системы составляет около 19 мкм, что даёт предельную разрешаемую частоту около 53 мм–1.

2.5

много, но видно, что на высоких частотах контраст немного выше 0,2, тогда как на рис. 5 д он немного меньше.

Таким образом, система, сформированная из неизображающих по отдельности линз, даёт изображение сопоставимого качества.

Рассмотрим ещё один пример неизображающей линзы. Теперь используем в качестве первой линзы параболическую обобщённую линзу с m = 1,9. Расстояние между линзами было таким же, как в предыдущем случае. В результате моделирования получено изображение светотехнической таблицы (рис. 7 а ). На рис. 7 б представлен график зависимости контраста от частоты линий для этой системы, который немного лучше, чем на рис. 5 д .

б) b

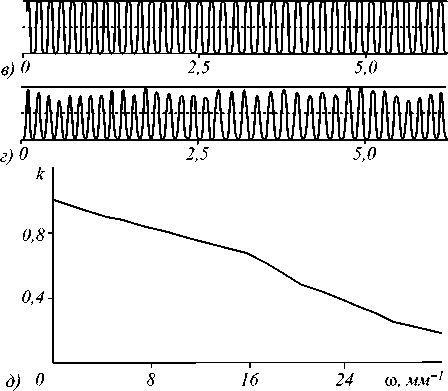
Рис. 5. Изображение радиальной светотехнической таблицы на выходе системы, состоящей из 2 параболических линз c m=2 (а), сечения по радиусам 0,95 мм (б), 0,5 мм (в), 0,3 мм (г), график зависимости контраста полос в изображении светотехнической таблицы в зависимости от частоты (д)

Рассмотрим, как изменится качество изображения при замене на параболические обобщённые линзы со степенью, отличной от 2.

Полученное в результате моделирования изображение показано на рис. 6.

к

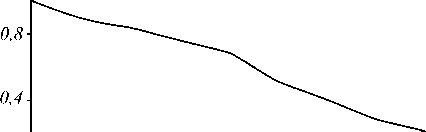
б) О              8            16           24    о.'./'./

Рис. 6. Изображение радиальной светотехнической таблицы на выходе системы, состоящей из параболической линзы c m=2,1, и компенсирующей линзы, рассчитанной по формуле (4), график зависимости контраста полос в изображении светотехнической таблицы в зависимости от частоты (б)

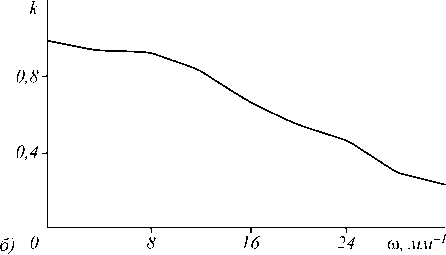
Рис. 7. Изображение радиальной светотехнической таблицы на выходе системы, состоящей из параболической линзы

c m = 1,9, и компенсирующей линзы, рассчитанной по формуле (4), график зависимости контраста полос в изображении светотехнической таблицы в зависимости от частоты (б)

При более существенных отличиях параболических обобщённых линз от линз с m =2 результаты принципиально не меняются. На рис. 8 а представлен пример изображения на выходе системы из обобщённой параболической линзы m =2,5 и соответствующей компенсирующей линзы.

Как видно из рис. 8 б, для этой пары линз полученный результат лучше, чем для линз с меньшими степенями.

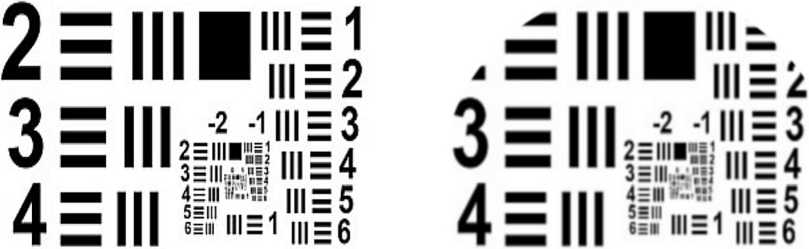
Такая система даёт изображение хорошего качества и для светотехнической таблицы нерадиальной структуры (рис. 9).

На рис. 9 б угловые участки отсутствуют, т.к. моделирующая программа строит изображение только в радиально симметричной области. Как видно из рис. 9 б, формируется изображение приемлемого качества, полностью сливаются только очень высокочастотные полосы.

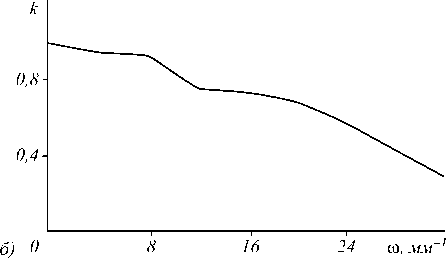
Рис. 8. Изображение радиальной светотехнической таблицы на выходе системы, состоящей из параболической линзы

c m = 2,5, и компенсирующей линзы, рассчитанной по формуле (4), график зависимости контраста полос в изображении светотехнической таблицы в зависимости от частоты (б)

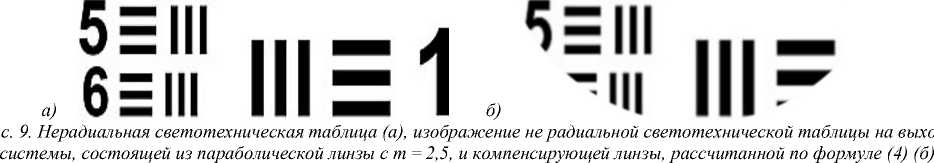
Заключение

Основной результат, полученный в работе, – принципиальная возможность формирования изображения в оптической системе, состоящей из неизображающих линз. Результат даёт основания утверждать о возможности разработки в будущем принципиально новых изображающих систем, основанных на использовании плоской аппроксимации асферических неизображающих линз. На основе анализа зависимости контраста от частоты полос можно утверждать, что для монохроматического излучения качество формируемого изображения телескопической системой обобщённых линз сопоставимо с качеством изображения, полученным в телескопической системе, состоящей из обычных параболических линз.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках госзадания (проект № 3.3025.2017/4.6, 007-ГЗ/Ч3363/26), а также при поддержке гранта РФФИ № 18-29-20045мк.