Изображающие свойства оптической системы с волноводом
Автор: Малов А.Н., Сенокосов Э.А., Рогожникова О.А., Фещенко В.С.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Технологии компьютерной оптики
Статья в выпуске: 25, 2003 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14058567
IDR: 14058567
Текст статьи Изображающие свойства оптической системы с волноводом
Ряд перспективных задач современной науки и техники, требуют поиска принципиально новых подходов к решению проблемы представления, передачи и обработки изображений [1-4].
В настоящее время, широко используется метод поэлементной передачи изображений по световодному жгуту с упорядоченным расположением изолированных друг от друга волокон [1], при этом каждое волокно жгута передает только одну точку изображения. На выходе из жгута формируется мозаичное изображение, составленное из отдельных точек.
Такая передача изображений имеет ряд недостатков: во-первых, ограничена разрешающая способность, связанная как с возможностью перекачки энергии из одного волокна в другое, так и с дифракцией света на торце каждого волокна. Во-вторых, потеря фазовой информации в изображении, т.е. переданное изображение является принципиально плоским. И, наконец, принципиально невозможно обработать изображение во время передачи.
Все вышеперечисленные ограничения составных волноводов стимулировали интерес к разработке методов передачи изображений по многомодовым волноводам [1].
1. Основная теория
Разрешающая способность волновода, как и любой другой оптической системы, определяется его апертурой. Апертура волновода, будет определяться его геометрическими параметрами и зависит от способа ввода излучения в волновод. Для диэлектрического волновода максимальная апертура ограничивается, так называемой числовой апертурой NA
NA = sin а = [ п 2 ( Л ) - п ^ С Л )]1 / 2, (1) где а - предельный угол ввода излучения в волновод; X - длина волны излучения; п о - коэффициент преломления сердцевины волновода; n 1 - коэффициент преломления оболочки.
Следовательно, максимальная разрешающая способность (предельная пространственная частота) для диэлектрического волновода определятся следующим выражением:
V ap = NA/ Л = [ п 2 ( Л ) - п 2 ( Л )]ш/ Л . (2)
Как видно, она не зависит от геометрических параметров и длины волновода.
Кроме того, существенное влияние на разрешающую способность диэлектрического волновода оказывает модовая структура поля внутри него. В [5] строго показано, что количество передаваемых деталей предмета равно количеству мод волновода, участвующих в создании изображения. Количество мод распространяющихся в планарном, диэлектрическом волноводе, согласно [2], будет
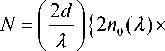
1/2 I
х [ n о ( Л ) - П 1 ( Л ) ] } + 2,
где d - толщина волноводного слоя.
Следовательно, разрешающая способность волновода, ограниченная модовой структурой поля, будет mod
(2 d / Л ) {2 п 0 ( Л )[ п 0 ( Л ) - п 1 ( Л )] }1/2 + 1/2
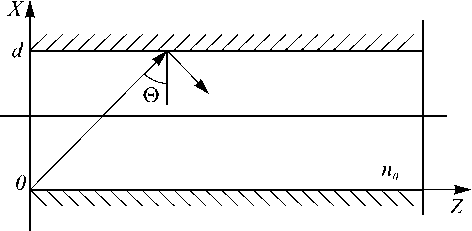
Рис. 1. Планарный волновод
W ( m ) =
= exp
= exp
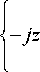
2 nn
n2
jz
4 d 2 n 0
11 2m |
2 ( 2 dn 0 J
( m 2
^^^^^^
В случае m >>1, ( m 2 - 1)
можно переписать в виде:
1 f 2 I 2 ( 2 dn 0 J
~ m 2 и выражение (11)
W ( m ) = exp[ - Jn2zm 2/4 d 2 n 0] (12)
Пусть входной торец волновода (z = 0) возбуждается монохроматическим источником света с распределением электромагнитного поля E 0( x ). Это распределение, с учетом апертуры волновода, можно представить в виде суперпозиции волновых функций волновода Fm(x) с амплитудами a m :
M
E о ( x ) = £ a m F m ( x ), (6)
m = 1
где М - номер предельной моды.
Распределение поля в произвольном сечении волновода z >> 2 так же определяется суперпозицией волновых функций волновода. Однако в отличие от сечения z = 0 в этой суперпозиции учитывается разница в константах распространения разных мод в m :
Ez ( x ) = exp( Jpx z ) x
# 3 (7)
X E a mFm ( x ) eXP( j z ( P m - в )" m = 1
Передаточная функция волновода тогда будет иметь вид:
W ( P m ) = exp[ jz ( P m - Д )]. (8)
Константу распространения в m можно найти согласно следующему выражению [1]:
, (9)
Пространственную частоту излучения в волноводе найдем исходя из, так называемого условия поперечного резонанса [7]:
2 k n 0 d ■ cos ® = 2 mn ,
где k = 2п/2 - волновой вектор, cos 0 - направляющий косинус, d - толщина волновода, m - номер моды.
Учитывая это условие, получим выражение для пространственной частоты в волноводе:
f = cos ® / 2 = m / 2 dn 0.
Подставляя (14) в (12) получим окончательный результат:
W ( f ) = exp - J---f2 .
L n 0 J
Или в двумерном случае:
W ( f x , /у ) = exp
-J— ( f x 1 + / . ’), n 0 J
2п
P m = Т » 0
1 | 2m
l 2 dn о.
где 2 - длина волны излучения, n0 - коэффициент преломления сердцевины волновода, d - толщина волновода.
Следовательно, передаточная функция (8) примет вид:
W ( m ) = exp
2n zz — П о
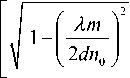
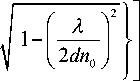
где fx = m / 2 dxn 0 , f y = n / 2 d y n 0 - пространственные частоты по оси х и по оси у соответственно; m и n -целые числа.
Выражение (16) полностью соответствует передаточной функции свободного пространства [6]. Следовательно, для компенсации разности фаз приобретаемой различными пространственными частотами может быть использован обычный объектив или линза.
Соотношение (16) верно и для многомодового диэлектрического волновода [1]. С той лишь разницей, что при всех расчетах необходимо использовать вместо истинной ширины волновода d некоторое его эффективное значение:
р
f 2 11 n I 1/2
def = d +l “ II 1 | ( n 0 - n1 ) , (17) l П Л n 0 J
где p = 0, для ТЕ-мод и p = 1 для ТМ-мод; n 0 и n 1 -показатели преломления волноводного слоя и оболочки ( n 0 > n 1 ).
Если учитывать только параксиальные моды, для которых выполняется неравенство 2 m/2dn0<< 1, выражение можно упростить путем замены корней первыми двумя членами их разложений в ряд:
Эксперимент
Волновод изготовлялся следующим образом. Стеклянная пластина ( n 0=1,55) погружалась в 1015%-й водный раствор желатина. Затем пластина сушилась в течение трех часов. В результате на по-
верхностях стеклянной пластины образовывался тонкий слой желатина ( n 1=1,54). Толщина волноводного слоя была от 1,5 до 3 мм. Длина волновода L была от 10 до 40 см.
Эксперимент проводился по схеме, которая изображена на рис. 2.
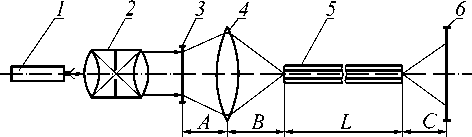
Рис. 2. Оптическая схема эксперимента
Пучок света от лазерного источника 1 попадает в коллимационную систему 2, где происходит его расширение и преобразование к параллельному. Затем параллельный пучок падает на прозрачный транспарант с изображением 3. После этого с помощью объектива 4 излучение вводится в волновод 5 и проходит сквозь него, а на экране 6 строится изображение транспаранта.
Мы применяли ввод света в волновод и его вывод с помощью призмы [7]. Это делалось с целью устранить влияние физической апертуры волновода на передачу через него изображения.
Изображение всегда наблюдалось в одной плоскости. Причем, только в том случае, когда расстояния транспарант – объектив, объектив – волновод и волновод – экран подчинялись формуле линзы:
111 --+ = —, A (B + C) F
где F – фокусное расстояние объектива, A – расстояние от транспаранта до линзы, В – расстояние от линзы до волновода, С – расстояние от волновода до экрана (причем В = С ).
В результате на экране в выходной плоскости системы было получено перевернутое изображение транспаранта (рис. 3).

Рис. 3. Изображение, полученное на экране в выходной плоскости системы
Изображение получилось растрированное. Параметры растра соответствовали формуле T = L/N , где Т – период растра, L – размер изображения, N – количество мод планарного волновода.
В случае, когда использовался планарный волновод с d =1,5 мм ( N =242), а размеры изображения на экране были L =20 мм, период растра был равен T « 0,083 мм. То есть разрешение системы в этих условиях было 12,1 мм-1, что сравнимо с разрешающей способностью промышленных объективов.
Обсуждение результатов эксперимента и выводы
Гипотеза о возможности компенсации фазовых набегов различных мод волновода одним обычным объективом подтвердилась. Хотя на результаты эксперимента влияют фундаментальные отличия процесса распространения света в волноводе от его распространения в свободном пространстве.
Во-первых, изображение получилось растри-рованным из-за дискретности Фурье-спектра в волноводе. Параметры растра (период и пространственное распределение его интенсивности) в точности соответствовали модовому составу планарного волновода. Таким образом, волновод сыграл роль фильтра пространственных частот.
Если еще раз обратить внимание на передаточную функцию волновода, то мы увидим, что волноводы с различной конфигурацией поперечного сечения, будут по-разному растрировать изображение. Форма растра будет зависеть от модового состава волновода (для прямоугольного волновода растр будет состоять из прямоугольников, для круглого – из концентрических колец и т.д.). Кроме того, в передаточную функцию волновода явным образом входит показатель преломления сердцевины волновода, это приведет к тому, что для градиентных волноводов моды высших порядков будут расположены ближе друг к другу. Вследствие этого увеличение изображения окажется неравномерным, и будет уменьшаться от центра изображения к его краям.
Во-вторых, в связи с тем, что Фурье-компоненты электромагнитного поля при распространении вдоль волновода, в условиях сохранения углов при распространении в волноводе, не могли расходиться в пространстве, то изменение длины волновода никак не влияло на конечный результат.
Это второе отличие процесса распространения света в волноводе от распространения его в свободном пространстве, при полной формальной идентичности передаточных функций, позволяет по-новому взглянуть на передачу изображений через волновод.
Можно, как и в свободном пространстве в зоне дифракции Френеля, встраивать в волноводный тракт компенсирующие элементы в виде линз. В этом случае мы получаем оптическую систему с увеличением, которое ограничено поперечными размерами волновода. И, соответственно, длина волноводного тракта будет ограничена фокусным расстоянием компенсирующего элемента. Для передачи изображения на расстояния более метра придется создавать волоконно-оптический аналог линзовой линии, что, и описано в [1]. Заметим, что подобная волоконно-линзовая линия может быть реализована с помощью локального осесимметричного сжатия круглого волокна с некоторым шагом по оси волокна (типа линии из механических «перехватов» – колец).
Получить же внутри волновода естественным путем дифракцию Фраунгофера не возможно, потому что Фурье-компоненты спектра электромагнитной волны не расходятся в пространстве, а только отстают друг от друга по фазе.
Таким образом, оптическая схема с объективом, который был вынесен за пределы волновода, оказалась гибче. В волноводный тракт был введен сразу Фурье-спектр, волновод его передал практически без изменений, и далее свободное пространство преобразовало Фурье-спектр в изображение. В этом случае объектив работал не только как компенсатор фазовых набегов различных пространственных частот и концентратор излучения, но и выступал как организатор электромагнитного поля внутри волновода, согласованного с его собственными модами.
С другой стороны волновод сам всегда выступает как фильтр пространственных частот. С этой точки зрения не важно, где помещать объектив, перед волноводом или же за ним. Фазы всех пространственных частот будут скомпенсированы в любом случае. Если будет соблюдаться соотношение (18), то изображения предметов, находящихся перед волноводом, успешно построятся, даже в том случае, если объектив расположить за волноводом. С той лишь разницей, что энергия, передаваемая через такую оптическую систему, будет сильно зависеть от физической апертуры волновода, которая, в этом случае, выступает, как входной зрачок системы.


