Изучение геометрических, термодинамических свойств и гибкости углеводородных молекул методом Монте-Карло

Одной из фундаментальных проблем физики конденсированного состояния является установление взаимосвязей между химическим строением и физическими свойствами разных молекул и молекулярных систем в различных условиях. Компонентами таких систем часто выступают молекулы цепного строения [6]. Типичный пример – углеводородные цепные молекулы. Информация об их физических и химических свойствах важна не только с научной точки зрения, но и для развития разных технологических отраслей, причем обе задачи тесно связаны между собой. А именно, обсуждаемые данные нужны для углубления знаний о структуре и функциях биологических систем, так как углеводородные цепи входят в состав молекул фосфолипидов мембран [1], [16]. С другой стороны, существование последних основано на эффектах самоорганизации, а принцип самоорганизации является одним из базовых принципов современных нанотехнологий. Несмотря на острую необходимость в данных по свойствам многих систем, они подчас скудны или

отсутствуют в литературе. В настоящей работе методом Монте-Карло (МК), алгоритм которого был разработан ранее [5], при температурах T = 293, 303, 313 K проведено моделирование 65 углеводородных цепных молекул с двойными связями cis , вида CH₃ – (CH₂) _a – (CH=CH – CH₂)_d – – (CH₂) _b – CH₃ (где a , b , d – целые), в невозмущенном состоянии (в Θ-условиях [6]), с количеством N атомов углерода (где N = a + b + 3d + 2), равным 16, 18, 20, 22, и количеством двойных связей d = 0, 1, 2, ..., 6. В работе [3] при моделировании перечисленных выше молекул этим методом были исследованы характеристики их формы, а в настоящей работе изучены равновесная гибкость, конформационная теплоемкость, относительные флуктуации квадрата радиуса инерции и квадрата расстояния между концевыми атомами углерода молекул.

Модель цепной молекулы и расчет средних характеристик

«Θ-условия», при которых вычисляли свойства всех молекул, примерно отвечают условиям в жидком или аморфном состояниях вещества [6], [10], [22]. Основные этапы расчета состояли в следующем (математические основы модели и алгоритма МК описаны в [3], [5]). Моделировали конформационное поведение одиночных цепей, среднее значение любой характеристики цепной молекулы вычисляли в NVT-ансамбле, причем оценку H этой величины получали методом МК. Генерировали углы внутреннего вращения (торсионные углы), определяющие конформацию молекулы, с использованием метода существенной выборки и учетом взаимозависимости каждых трех углов вдоль по цепи; при этом предполагали, что они могут принимать значения в диапазоне 0–360°. Конформационную энергию цепи рассчитывали с помощью атом-атомных потенциальных функций с параметрами силового поля CHARMM27 [11], [14], учитывали взаимодействия только тех атомов, которые расположены в пределах фрагментов вдоль по цепи (ближние взаимодействия). Фрагменты точно передавали детали химического строения и были выбраны так, чтобы учесть взаимозависимость изменения каждых трех последовательных торсионных углов молекулы. Любая пара смежных фрагментов перекрывалась: два их торсионных угла были общими. Выборка значений углов внутреннего вращения осуществлялась с плотностью вероятностей, учитывающей энергию ближних взаимодействий молекулы. В итоге вычисляли средние характеристики каждой молекулы. В частности, вычислены средние значения квадрата радиуса инерции:

где R _c – радиус-вектор центра масс рассматриваемой цепи:

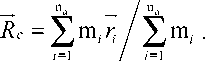
Здесь m . (i =1, 2, .„, n a ) - массы атомов; ^ (где i = 1, 2, …, n _a ) – радиус-векторы атомов в данной конформации; n _a – общее количество атомов. Вычислены средние квадраты расстояний 2> между концевыми атомами углерода молекул. Исследованы относительные флуктуации ( е 2 и ^ ₂) величин S и h² соответственно:

^ 2 = « S 4) Ч S 21 )/( S 2)2’

е =(( 4ЧИ)/Ч’>.

Изучена равновесная гибкость молекул; в качестве меры гибкости использовано отношение /L [4], где – среднее расстояние между концевыми атомами углерода, L – контурная длина молекулы [6]. Величину L данной молекулы вычисляли как сумму длин максимально вытянутых конформаций участков цепи без двойных связей и с двойными связями. Очевидно, 0 < /L < 1, и чем меньшим у данной молекулы оказывается отношение /L, тем более гибкой она является. Наконец, были вычислены величины конформационной теплоемкости CV = ∂/∂T = (-()2)/(kB∙T 2) [2; 80] и «удельной» конформационной теплоемкости CV/Nφ. Здесь U – потенциальная энергия ближних взаимφ одействий молекулы, T – температура, kB – постоянная Больцмана, Nφ = (N-d-3) – количество углов внутреннего вращенφия вокруг простых C-C связей цепи, содержащей N атомов углерода и d двойных связей; 2 угла, отвечающие вращениям концевых CH3-групп вокруг связей CH2-CH3, исключены, поскольку их изменение почти не влияет на энергию U.

Описание строения молекул

Полное описание строения любой из рассматриваемых здесь углеводородных молекул требует указания общего количества атомов углерода (N) в ней, количества двойных связей (d), а также их положения в цепи. Последнее в общем случае требует указания еще d чисел. Однако перечислять положения каждой двойной связи не обязательно, поскольку химическое строение этих молекул специфично : между каждой парой двойных связей расположена только одна группа CH₂, и положение всех двойных связей легко вычисляется, если известно, например, местоположение только первой двойной связи. Для этого можно задать параметр Δ [17] – номер атома углерода, ближайшего к заданному концу цепи и участвующего в образовании первой (от данного конца цепи) двойной связи. Атомы углерода при этом имеют номера от 1 до N подряд вдоль по цепи, начиная от одного из концевых. Положение всех двойных связей с помощью одного параметра можно описать и другим способом: указать местоположение X их «центра» [17], которое равно среднему арифметическому номеров атомов углерода, участвующих в образовании всех двойных связей. Например, если молекула содержит одну двойную связь, расположенную между 9-м и 10-м атомами углерода, то Δ = 9, а X = (9 + 10)/2 = 9,5; если молекула содержит 2 двойные связи, расположенные между 6-м и 7-м, 9-м и 10-м атомами углерода, то Δ = 6, а X = (6 + 7 + 9 + 10)/4 = 8, и т. д. В зависимости от обстоятельств в настоящей работе использован 1-й или 2-й вариант идентификации молекул (N, d, Δ или N, d, X). Параметры N, d, Δ в обозначениях молекул указаны сокращенной формулой N:d w ^cis.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Численные значения ряда полученных в настоящей работе характеристик (< S >, < S ²>, ,

• 2>) для некоторых молекул и соответствующие данные литературы [8], [9], [10], [12], [13], [15], [17], [18], [19], [20] представлены в таблице; в целом они согласуются между собой. Важно отметить, что в большинстве работ приведены данные лишь для отдельных молекул или неболь-

• ших групп, а в настоящей работе в идентичных условиях исследована большая их совокупность (65 молекул). Это позволяет выявить взаимосвязь между химическим строением молекул и свойствами веществ. При этом следует учесть, что на результаты могут оказывать влияние избранная

Характеристики* размеров углеводородных цепных молекул, полученные в эксперименте или при компьютерном моделировании (в расплаве или Θ-условиях). Параметры N, d, Δ в обозначениях молекул указаны сокращенной формулой N:dω Δcis

Молекула	T , K	< S >, Å	(< S 2>)1/2, Å	< S 2>, Å2	, Å	(2>)1/2, Å	2>, Å2	Метод**	Ссылка
16:0	298			22±2				НР	[10]
	298	4.9±0.2						МК	[12]***
	298			26.02±0.03			226.5±0.4	МД-а	[15]
	298			23.10±0.04			189.3±0.6	МД-б	[15]
	303	5.04±0.01			14.67±0.01			МК	[8]
	303	4.909±0.001		24.26±0.01	13.95±0.01		199.9±0.1	МК	Наст. раб.
	313	4.903±0.001		24.20±0.01	13.92±0.01		199.2±0.1	МК	Наст. раб.
	318	4.8±0.2						НР	[13]
	323			25.34±0.02			217.5±0.2	МД-а	[15]
	323			22.66±0.02			183.7±0.3	МД-б	[15]
	373			24.49±0.02			206.8±0.3	МД-а	[15]
	373			21.94±0.02			175.1±0.3	МД-б	[15]
18:0	278	5.10±0.01		26.54±0.02	14.16±0.01		214.6±0.2	МК	[17], [18]*****
	298	5.3±0.1						МК	[12]***
	303	5.05±0.01		26.06±0.01	13.95±0.01		208.8±0.2	МК	[17],[18]*****
	303	5.391±0.001		29.30±0.01	15.28±0.01		241.3±0.1	МК	Нас т. раб.
	313	5.384±0.001	5.406±0.001	29.22±0.01	15.25±0.01	15.51±0.01	240.5±0.1	МК	Наст. раб.
	323				15.84±0.07			МК	[20]****
	497.5		4.92±0.01			13.52±0.07		БД	[19]
18:1 to 9cis	313		5.010±0.001			14.09±0.01		МК	Наст. раб.
	497.5		4.80±0.01			13.18±0.04		БД	[19]
18:2 to 6cis	278	4.52±0.01		20.91±0.1	11.99±0.04		157.9±0.8	МК	[17], [18]*****
	313	4.745±0.001	4.769±0.001	22.74±0.01	12.92±0.01	13.31±0.01	177.1±0.1	МК	Наст. раб.
	497.5		4.47±0.01			11.66±0.05		БД	[19]
18:3 to 3cis	278	4.39±0.04		19.73±0.3	11.34±0.2		141.2±3.0	МК	[17], [18]*****
	313	4.655±0.001	4.678±0.001	21.88±0.01	12.59±0.01	12.94±0.01	167.4±0.2	МК	Наст. раб.
	497.5		4.32±0.01			10.60±0.05		БД	[19]
18:4 to 3cis	278	4.10±0.02		17.20±0.2	10.16±0.1		116.0±2.0	МК	[17], [18]*****
	313	4.446±0.001		19.94±0.01	11.91±0.01		150.3±0.2	МК	Наст. раб.
18:5 to 3cis	278	3.96±0.01		16.06±0.01	9.46±0.01		101.4±0.2	МК	[17], [18]*****
	303	3.95±0.01		16.05±0.01	9.47±0.01		101.5±0.2	МК	[17], [18]*****
	313	4.369±0.002		19.26±0.02	11.60±0.02		141.9±0.4	МК	Наст. раб.
20:0	298	5.7±0.1						МК	[12]***
	303	5.856±0.001		34.61±0.01			284.1±0.1	МК	Наст. раб.
	313	5.848±0.001		34.52±0.01			283.0±0.1	МК	Наст. раб.
	318	5.1±0.3						НР	[13]
	500			36.17±0.01			312.7±0.1	МК	[9]
	500			36.18±0.01			313.6±0.1	МК	[9]
	500			36±1			311±15	МД	[9]

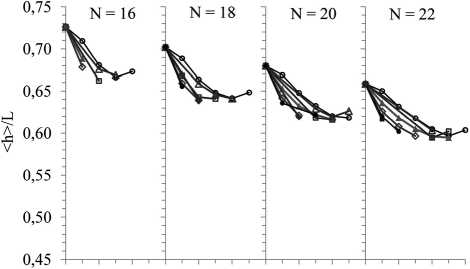
0240240240246 d

Рис. 2. Зависимости отношений /L (где – среднее расстояние между концевыми атомами углерода цепи, L – ее контурная длина) от количества d двойных связей cis для невозмущенных углеводородных молекул с параметром Δ = 3 (       ), 4 (       ), 5 (        ), 6 (       ), 7 (       ),

8 (     ), 9 (     ), 11 (     ) по группам молекул с одина ковым количеством N атомов углерода. Параметр Δ – номер атома углерода, участвующего в образовании первой двойной связи от конца цепи. Расчет методом МК при температуре T = 293 K. Доверительные интервалы, отвечающие 95%-ной надежности согласно t-распределению Стьюдента, меньше размеров символов на графиках d = Const и N = Const, тем, как правило, больше ее гибкость (см. рис. 1). Этот эффект объясняется разной степенью влияния наиболее низкоэнергетических (свернутых) конформаций фрагментов, содержащих двойные связи. Если фрагмент с двойными связями расположен у конца цепи, свернутые конформации оказываются в известном смысле «локальными» по сравнению с вытянутыми низкоэнергетическими конформациями оставшегося (насыщенного) участка цепи. Нали- чие такого фрагмента вблизи середины цепи разделяет насыщенную часть молекулы на 2 участка, низкоэнергетические конформации которых в общем случае вытянуты в разных направлениях, что уменьшает расстояние .

Конкурентное влияние на величину /L количества двойных связей d и их местоположения X (или Δ ) можно назвать «d – X – конкуренцией» или «d – Δ – конкуренцией». Вследствие такой конкуренции и могут возникнуть упомянутые выше ситуации, когда при N = Const молекула с большей степенью ненасыщенности (d₁ двойных связей) является менее гибкой, чем менее ненасыщенная молекула (d₂ двойных связей, d₂< d₁). В случае реализации такой ситуации в первой молекуле d₁ двойных связей расположены, как правило, у одного из ее концов, а во второй молекуле d₂ двойных связей – вблизи середины цепи (см. рис. 1).

Наконец, при d = Const и X = Const гибкость молекулы растет (/L уменьшается) с ростом N для всех рассмотренных N (см. рис. 1).

Обсуждаемые для /L закономерности коррелируют с таковыми работы [4], несмотря на упомянутую выше разницу в моделях. Иными словами, использованный метод моделирования позволяет выявлять основные тенденции, определяющие влияние химического строения на свойства молекул.

Относительные флуктуации геометрических размеров . Наблюдается рост флуктуаций E h 2 (рис. 3) для всех моноеновых и диеновых цепей (d = 1, 2), а также достаточно длинных (N = 18, 20, 22) триеновых и тетраеновых цепей (d = 3, 4) при смещении X от концов к середине цепи. Если количество двойных связей в цепи еще больше (d = 5 и 6), то величина E h 2 зависит от параметра X немонотонно. Аналогично ведут себя относительные флуктуации E S 2 (данные здесь не представлены), хотя их амплитуда значительно, примерно в 5 раз, меньше, чем амплитуда E h 2 . Последнее вполне объяснимо: S вычисляется с учетом взаимных положений всех атомов молекулы, тогда как h² – только двух концевых атомов углерода. Отметим, что общие тенденции, которые отражают зависимости величины E _h2 от параметра X (см. рис. 3), качественно согласуются с тенденциями изменения от этого параметра величины гибкости, характеризуемой отношением /L (см. рис. 1): чем более гибкой является молекула (то есть чем меньше /L), тем больше и флуктуации ее геометрических размеров (в этом смысле величина E _h2 может служить своеобразной мерой гибкости). Увеличение флуктуаций E h₂ (и E S 2 ) при смещении X от концов к середине цепи, при N = Const, d = Const, как и увеличение ее гибкости, связано с описанными выше особенностями строения молекул и внутренних вращений.

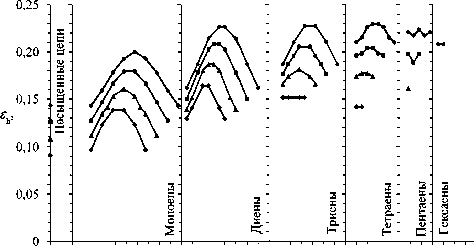
О 4 8 12 16 4 8 12 16 4 8 12 16 8 12 8 12 12 16

X

Рис. 3. Зависимости относительных флуктуаций £ ^ 2 квадратов расстояний между концевыми атомами углерода невозмущенных углеводородных молекул от параметра X. Условия и обозначения, как на рис. 1

Удельная конформационная теплоемкость . Конформационная теплоемкость, приходящаяся на один угол вращения вокруг простой связи C-C, соседней с двойной (в ненасыщенных цепях), меньше, чем вокруг простой связи C-C в насыщенном участке цепи. Этот вывод следует из сравнения данных, например, для цепей 16:0 и 22:6 w 3 cis (рис. 4). Для обеих молекул N_φ = 13. Величина C_V/N_φ для цепи 16:0 приходит-ся^φ на угол вращения тол^φько вокруг простой связи C-C (углов другого типа N_φ не содержит). Для цепи 22:6 w 3 cis она почти полностью приходится на угол вращения вокруг связи C-C, соседней с двойной (таких углов 12 из 13). Различие между величинами C /N вызвано тем, что, как

Vφ упоминалось выше, первый торсионный барьер (~3 ккал/моль) больше, чем второй (~2 ккал/моль); минимумы поверхностей энергии в ненасыщенной цепи более пологие. В результате плотность высокоэнергетических состояний в насыщенной цепи оказывается больше, чем в ненасыщенной. С увеличением в молекуле количества двойных связей, то есть с ростом доли простых C-C

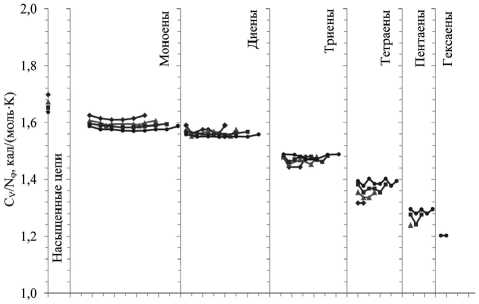
0 4 8 12 16 4 8 12 16 4 8 12 16 8 12 8 12 12 16 X

Рис. 4. Зависимости от параметра X удельных конформационных теплоемкостей C /N , связанных с флуктуаци-

Vφ ями энергии ближних взаимодействий невозмущенных углеводородных молекул. Условия и обозначения, как на рис. 1

связей, соседних с двойными, величина CV/Nφ молекулы постепенно уменьшается (см. рис. 4)φ. Удельная теплоемкость в цепях с N = Const, d = Const почти не зависит от X (см. рис. 4), поскольку при этом доля простых C-C связей, примыкающих к двойным, остается постоянной. Вклад внутреннего вращения в теплоемкость различных молекул цепного строения весьма важен; он обсуждается, например, в обзоре [21].

Итак, в работе установлена связь между химическим строением широко распространенных в природе цепных углеводородных молекул и относительными флуктуациями их геометрических размеров, а также конформационной теплоемкостью, связанной с флуктуациями энергии ближних взаимодействий, обобщен ряд тенденций изменения равновесной гибкости молекул. Полученные данные способствуют углублению общего понимания взаимосвязей между структурой и свойствами данного класса молекул.

• * Работа выполнена при поддержке программ президента РФ «Ведущие научные школы» (гранты НШ-1642.2012.4, НШ-1410.2014.4).