Изучение эффективности восстановления изображений в методе однопиксельной визуализации с помощью генеративных состязательных сетей

Наиболее распространённые сегодня методы формирования изображений используют многопиксельные матричные фотосенсоры, что позволяет получить требуемое пространственное разрешение целевого объекта. Такие методы лежат в основе многочисленных фото- и видеоустройств, от мобильных телефонов и цифровых камер до специализированного профессионального оборудования. Несмотря на превосходные характеристики матричных сенсоров, их использование в нестандартных режимах работы сталкивается с серьезными трудностями. Например, технологически сложно создать сенсор с гибко настраиваемым спектральным диапазоном вне диапазона чувствительности кремния или же добавить к высокому пространственному разрешению высокое временное разрешение.

Альтернативным способом получения изображений является метод однопиксельной визуализации. Идея метода заключается в освещении объекта про- странственно-модулированным светом (световыми паттернами), измерении общего количества света, отраженного от объекта, и вычислении пространственного изображения объекта по полученной таким образом информации [1]. Пространственная модуляция света может быть реализована в широком спектральном диапазоне, например с помощью цифровых мик-розеркальных модуляторов света [2, 3]. Однопиксельная визуализация открывает качественно новые возможности получения изображений. Например, можно получать изображения в диапазоне длины волны 1,5 микрона на уровне одиночных фотонов [4], мультиспектральные изображения [5], трехмерные изображения [6, 7], рентгеновские изображения [8, 9].

Вычислительная часть метода однопиксельной визуализации заключается в решении системы уравнений, связывающих измеренные сигналы однопиксельного детектора и световые паттерны. В последнее время методы машинного обучения продемонстрировали большой потенциал в решении этой задачи [10 – 12]. Нейросетевые методы оказались успешны в за- дачах, близких задаче восстановления изображения, как например: в задаче классификации изображений [13], оптимизации световых паттернов для однопиксельной визуализации [14], определении расстояния до объекта [15].

Недавно было показано успешное применение концепции генеративных состязательных сетей в методе однопиксельной визуализации [16– 18]. Однако вопрос построения оптимальной архитектуры нейронной сети для этой цели остается открытым, так как сравнения разных типов генеративных состязательных сетей и качества работы генеративных состязательных сетей при наличии аппаратных искажений в однопиксельной визуализации до настоящего времени не проводилось. В данной работе мы сравниваем качество восстановления изображения в однопиксельной визуализации, осуществленного с помощью двух видов генеративных состязательных сетей – глубокой сверточной генеративной состязательной сети и генеративной состязательной сети наименьших квадратов. Нами установлено, что генеративная состязательная сеть наименьших квадратов демонстрирует несколько лучшее качество восстановления изображения по сравнению с глубокой сверточной генеративной состязательной сетью. В то же время при наличии аппаратных искажений в виде изменения поля зрения камеры глубокая сверточная сеть стабильно обучается восстановлению изображений с более высоким качеством, чем генеративная состязательная сеть наименьших квадратов.

Статья организована следующим образом: в параграфе 1 приводятся основные сведения о методе однопиксельной визуализации, в параграфе 2 приводится описание процесса обучения анализируемых генеративных состязательных сетей, в параграфе 3 приводится описание процедуры генерации паттернов для однопиксельной камеры, в параграфах 4 и 5 приводятся результаты моделирования работы однопиксельной камеры и восстановления изображений при отсутствии (параграф 4) и при наличии (параграф 5) аппаратных искажений поля зрения камеры.

1.    Однопиксельная визуализация

Получение изображения методом однопиксельной визуализации можно условно раздлелить на два этапа. Первый этап однопиксельной визуализации заключается в детектировании пространственно модулированного света, отраженного от объекта, с помощью однопиксельного детектора, измеряющего интегральную интенсивность света без простраственного разрешения. Допустим, мы хотим построить изображение объекта шириной W и высотой H пикселей. Свет от источника (непрерывного или импульсного) направляется на цифровое микрозеркальное устройство, которое проецирует матричный паттерн Pi =(pi,...,pWH) для пространственной модуляции отраженного света. Отраженный от объекта свет со- бирается посредством линзы на детекторе, который измеряет интегральное значение интенсивности отраженного света si для выбранного паттерна. Эту процедуру можно провести для M различных матричных паттернов и записать уравнение

S=PI, (1)

где в векторной форме представлены изображение целевого объекта I =(i 1 ,…, i WH ), матрица паттернов P = ( P 1 ,...,P M ) ^T и набор интенсивностей, измеренных для M паттернов S =( s 1 ,…, s M ). Отношение количества использованных паттернов M к размеру матрицы паттерна WH называется частотой выборки SR = M / WH (sampling rate).

Вторым этапом однопиксельной визуализации является восстановление целевого изображения I по значениям интенсивностей S и информации об использованных паттернах P . В случае, когда для получения изображения используется столько паттернов, сколько пикселей в изображении ( M = WH , SR = 1), результирующее изображение I является решением системы линейных уравнений

I = P ^{- 1} S . (2)

На практике число паттернов может быть не равно числу пикселей. С одной стороны, наличие шума в сигнале требует увеличения числа паттернов. С другой стороны, реальные изображения имеют некоторую избыточность в своей структуре, поэтому могут быть восстановлены с меньшим числом паттернов методами сжатого сэмплирования или машинного обучения.

2.    Генеративные состязательные сети

Генеративная состязательная сеть представляет собой нейронную сеть, состоящую из двух компонент – сети-генератора G ( z , θ G ) и сети-дискриминатора D ( x , θ D ). Здесь z – входной вектор (в нашем случае – вектор интенсивностей, полученный в результате работы однопиксельной камеры), из которого генератор создаёт изображение, x – изображение (реальное или сгенерированное), которое классифицирует дискриминатор, а θ D ( G ) – набор настраиваемых параметров дискриминатора (генератора). Обе нейросети в нашем случае представляют собой свёрточные нейросети с архитектурой, соответствующей требуемым выходным данным: на выходе генератора получается изображение размером WH , а на выходе дискриминатора получается вещественное число в диапазоне между 0 и 1, характеризующее вероятность того, что поданное на вход изображение не было сгенерировано сетью-генератором.

Схематично процесс обучения нейросетей имеет следующий вид. Пусть имеется обучающая выборка изображений («истинные» изображения). Для каждого изображения мы получаем вектор отсчётов интенсивностей посредством симуляции работы однопиксельной камеры (см. параграф 1), и для каждого такого вектора сеть-генератор восстанавливает изображение объекта («сгенерированные» изображения). В процессе обучения сети-дискриминатора на вход дискриминатора попеременно подаются истинные и сгенерированные изображения с соответствующей меткой (1 для истинных и 0 для сгенерированных изображений) и дискри- минатор обучается правильной разметке подаваемых изображений. В процессе обучения сети-генератора сгенерированные сетью-генератором изображения подаются на вход сети-дискриминатора. Сеть-генератор настраивается в сторону увеличения вероятности присвоения метки 1 («истинное» изображение) сгенерированному изображению.

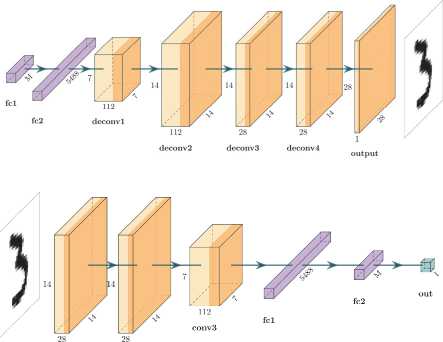
convl       conv2

Рис. 1. Схема архитектуры нейронной сети: сеть-генератор (сверху) и сеть-дискриминатор (снизу). На вход сети-генератора подаётся вектор отсчётов интенсивностей размером M, полученный в результате работы однопиксельной камеры. На выходе сети-генератора появляется восстановленное изображение объекта. На вход сети-дискриминатора подаётся изображение объекта – сгенерированное сетью-генератором или истинное. На выходе сети-дискриминатора появляется число от 0 до 1, характеризующее вероятностью поданного на вход изображения быть истинным (не сгенерированным сетью-генератором)

Процесс обучения генеративной состязательной сети заключается в попеременной оптимизации параметров двух нейросетей с соответствующими функциями ошибок. Первая стадия обучения – обучение дискриминатора D , при котором дискриминатору демонстрируются изображения из обучающей выборки («истинные» изображения), а также сгенерированные сетью G изображения. Задачей дискриминатора является разметка изображений на истинные и сгенерированные. Функцией ошибки дискриминатора для глубокой сверточной генеративной состязательной сети является бинарная кросс-энтропия [19]

L DDC ( D ) = E x [ log ( D ( x ))] + E z [ log (1 - D ( G ( z )))], (3)

а для генеративной состязательной сети наименьших квадратов [20]

L DS ( D ) = 2 E x [( D ( x ) - 1) 2 ] + 2 E z [( D ( G ( z ))) 2 ],    (4)

где усреднение производится по подвыборке истинных изображений x или по подвыборке векторов отсчётов z. Вторая стадия обучения – обучение генератора G. На этой стадии сгенерированные генератором изображения подаются на вход дискриминатору попеременно с реальными изображениями, а дискриминатор (с фиксированными на этой стадии параметрами) размечает изображения на реальные и сгенериро- ванные. Задачей генератора является научиться генерировать изображения таким образом, чтобы генератор не мог достоверно отличить сгенерированные изображения от реальных. Функция ошибки для генератора в глубокой сверточной генеративной состязательной сети [19] имеет вид

L dgc ( G ) = E z [ log ( D ( G ( z )))], (5)

а для генеративной состязательной сети наименьших квадратов [20]

L GS ( G ) = 2 E z [( D ( G ( z )) - 1) 2 ]. (6)

На первой стадии обучения минимизируется функция L ^D _D ^{C ( LS )} ( D ) и настраиваются параметры сети-дискриминатора D , тогда как на второй стадии обучения минимизируется функция L ^D _G ^{C ( LS )} ( G ) и настраиваются параметры сети-генератора G . В результате обучения получается сеть-генератор, способная восстанавливать изображение из вектора интенсивностей, полученного с помощью съемки целевого объекта посредством однопиксельной камеры. Обученная сеть способна восстанавливать изображения объектов, не присутствующих в обучающей выборке.

Помимо конкурентной составляющей процесса обучения дискриминатора и генератора в функции ошибок генератора входят дополнительные компо- ненты, позволяющие генератору создавать более качественные изображения. Такие дополнительные компоненты функции ошибок называются в литературе функциями ошибок содержания (content loss). В данной работе используются две дополнительные функции ошибок: функция ошибок L1

WH

L 1 = _W ¹ _H ∑ _{i =1} ∑ _{j =1} | x i , j - G ( z ) i , j |, (7)

где x i,j – компоненты истинного изображения и G ( z ) i,j – компоненты восстановленного генератором изображения, и функция ошибок, основанная на нейросети VGG19 (perceptual similarity loss) [21]:

WkHk

L VGG =¹ ∑∑ ( VGG k ( x ) i , j - VGG k ( G ( z )) i , j ) ² ,(8) W k H k i =1 j =1

где VGG k – k -й слой нейронной сети VGG19, и VGG k ( x ) i,j – выход k -го слоя VGG19 для поданного на вход изображения x , W k и H k – ширина и высота результата на выходе k -го слоя VGG19.

3.    Генерация паттернов

Важным вопросом в задаче однопиксельной визуализации является выбор паттернов, поскольку он напрямую влияет на её быстродействие и качество. С точки зрения скорости визуализации выбор бинарных паттернов представляется естественным, поскольку позволяет использовать каждое микрозеркальце цифрового микрозеркального устройства как один пиксель паттерна. В то же время выбор бинарных матриц, обеспечивающих наилучшее качество визуализации, неоднозначен. Например, использование случайных бинарных паттернов с фиксированным соотношением 0 и 1 вместе со сжатым сэмплированием требует большого (не менее 300 для изображения с 784 пикселями) количества паттернов для достижения приемлемого качества восстановленного изображения [22]. В то же время использование таких паттернов вместе со свёрточной нейронной сетью для классификации изображений демонстрирует хорошие результаты [23]. Таким образом, один и тот же способ генерации паттернов может показывать разную эффективность в разных задачах.

Использование нейронных сетей в однопиксельной визуализации позволяет (помимо восстановления изображений) генерировать оптимальные (для конкретной задачи) паттерны. Так, в работе [14] сверточный автокодировщик использовался для одновременного восстановления изображений из значений интенсивностей, измеренных однопиксельной камерой, и для генерации паттернов, оптимальных для работы камеры.

В данной работе мы используем набор паттернов, сгенерированных сверточным автокодировщиком, обученным восстановлению изображений из набора MNIST. Кодирующая часть сверточного автокоди- ровщика состоит из одного полносвязного слоя, переводящего N (784 в нашем случае) пикселей изображения в M (64 в нашем случае) переменных скрытого слоя; такая архитектура была выбрана для того, чтобы матрица весов кодировщика по размеру соответствовала матрице паттернов P.

Процесс обучения сверточного автокодировщика состоял из трёх этапов:

• •    на первом этапе кодировщик и декодировщик обучались совместно без каких-либо ограничений. Обучение было прервано на моменте, когда значения функции потерь перестали значимо изменяться для обучающего и тестового набора;

• •    на втором этапе был введен дополнительный член функции потерь вида:

MN

Lrenorm =R*∑∑wm2n *(1-wmn)2, (9) mn где R – константа, wmn – веса кодировщика. Этот член «штрафует» нейронную сеть, если значения весов кодировщика слишком сильно отличаются от 0 или 1. В процессе дообучения свёрточного автокодировщика константа R увеличивалась несколько раз для достижения различия весов кодировщика wmn от нуля (либо единицы) не более чем 10–3;

• •    на третьем этапе веса кодировщика были зафиксированы, округлены до целого значения и использованы как матрица паттернов P.

4.    Восстановление изображений при отсутствии аппаратных искажений

Таким образом, с помощью весов кодировщика была получена бинарная матрица паттернов P для эффективного кодирования изображений в сигналы S .

Обучение генеративных состязательных сетей осуществлялось на наборе изображений MNIST, состоящем из 60000 изображений в обучающей выборке и 10000 изображений в тестовой выборке. Задачей генератора являлось восстановление изображения цифры от 0 до 9 из симулированных результатов работы однопиксельной камеры, а задачей дискриминатора – разметка изображений на реальные и сгенерированные. Генератор состоял из 2 входных линейных полносвязных слоёв и 4 слоёв обратной свертки с функциями активации ReLU f ( x )= max (0, x ) на 3 внутренних слоях и с сигмоидной выходной функцией f ( x )= 1 /(1 + e^–x ) на последнем. Дискриминатор состоял из 3 сверточных слоёв с функциями активации Leaky ReLU f ( x )= max (0,01, x ) и 2 выходных линейных полносвязных слоёв с сигмоидными функциями активации. Минимизация функций ошибок осуществлялась оптимизатором RMSProp с начальной скоростью обучения lr = 4×10^–4 для генератора и дискриминатора, а также параметром α = 0,99. Обучение длилось в течение 50 эпох, при этом каждые 5 эпох скорость обучения для обеих компонент сети падает в

2 раза. Обучающая выборка разбивалась на подвыборки (батчи) по 30 изображений, и каждые 10 эпох размер подвыборки увеличивался вдвое. Для оценивания качества восстановления изображений сетью-генератором использовались метрики Peak Signal-to-Noise Ratio (PSNR)

PSNR ( x , x )=10 log 10 ( _M ^M _SE ^ax ₍ ⁽ _x ^x _, ⁾ _{x )})               (10)

и Structural Similarity Index Measure (SSIM)

SSIM ( x , x ) = (2 ^{2 ц} x Ц x ^{+ C} 1 )⁽²₂ ^g xx + c ² ) , (11) ( ц ² + Ц 2 + c 1 )( c ² + G ² + c ₂ )

где x – истинное изображение, x = G ( z ) – изображение, восстановленное сетью-генератором из вектора интенсивностей z , ц _x ( _x ) - среднее значение матричных элементов в изображении x ( x ), a _x ( _x ) - дисперсия значений матричных элементов в изображении x ( x ), а a _xx - коэффициент корреляции между изображениями x и x .

Рис. 2. Используемый в данной работе набор паттернов, который был сгенерирован свёрточным автокодировщиком

Две генеративные состязательные сети были обучены на бесшумовых изображениях из набора MNIST для различных (1 %, 2%, 4% и 8%) частот выборки однопиксельной визуализации. Генераторы обученных сетей восстанавливали изображения из тестовой части набора, и вычислялись средние значения метрик PSNR и SSIM на тестовых изображе- ниях. Графики средних значений метрик от частоты выборки представлены на рис. 3. Полученные зависимости показывают, что генеративная состязательная сеть наименьших квадратов достигает несколько лучшего по сравнению с глубокой сверточной генеративной состязательной сетью качества восстановления изображений.

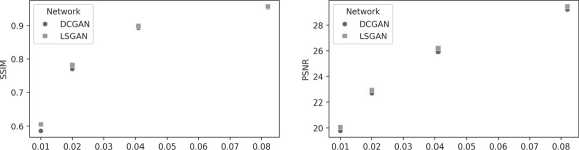
Sampling rate                                                     Sampling rate

Рис. 3. Зависимости средних значений метрик PSNR и SSIM от частоты выборки однопиксельной камеры для изображений, восстановленных генераторами обученных генеративно-состязательных сетей

На рис. 4 представлены примеры восстановления изображений цифр генераторами двух нейронных сетей, а также истинное изображение цифры (до выборки с помощью однопиксельной камеры). Представлены примеры трёх цифр для демонстрации того, что качество восстановления может быть различным для различных цифр: цифра может восстанавливаться хорошо вплоть до низких частот выборки (цифра «9» на рис. 4) или же значительно искажаться при низких частотах выборки (цифра «5» на рис. 4). В то же время при частоте выборки 8% все цифры восстанавливаются без существенных искажений.

5.    Восстановление изображений при наличии аппаратных искажений

Генеративные состязательные сети двух типов были обучены на изображениях из набора MNIST, содержащих аппаратные искажения. В качестве аппаратного ис- кажения рассматривалась тёмная рамка вокруг изображения, соответствующая неточности в расположении визуализируемого объекта, приводящей к излишне большому полю зрения объектива камеры. Для набора статистики было обучено 10 генеративных состязатель- ных сетей каждого вида со случайно инициализированными параметрами. Обучение каждой сети длилось в течение 10 эпох, поскольку при рассматриваемых параметрах симуляции сети достигали своего наилучшего обученного состояния в течение 10 эпох.

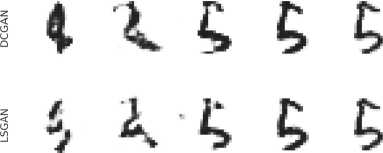
SR = 0.01 SR = 0.02 SR = 0.041 SR = 0.082 Ground truth

Рис. 4. Примеры цифр, восстановленных генераторами обученных генеративных состязательных сетей при различных частотах выборки, а также истинные изображения цифр

! 4 <7 9 4 9

। 9 ^ q 9 9

SR = 0.01 SR = 0.02 SR = 0.041 SR = 0.082 Ground truth

На рис. 5 представлены значения метрик PSNR и SSIM для 10 генеративных состязательных сетей каждого вида, обученных на восстановление изображений с однопиксельной камеры при частоте выборки 8 %. Значения метрик вычислялись на 10000 тестовых изображениях цифр. Из полученных результатов видно, что после добавления аппаратных шумов глубокая сверточная генеративная состязательная сеть обучается восстановлению изображений стабильно лучше, чем генеративная состязательная сеть наименьших квадратов. Несмотря на то, что сеть наименьших квадратов способна обучиться до высокого качества (сеть LS10 на рис. 5), при других инициализациях начальных параметров процесс обучения может закончиться со значительно более низким качеством восстановления изображений (сети LS8 и LS9). Возможной причиной такого поведения является различие в свойствах сходимости конкурентной части функции ошибок двух сетей: в случае глубокой сверточной генеративной состязательной сети конкурентной частью функции ошибок является бинарная кроссэнтропия (формулы (3), (5)), а для генеративной состязательной сети наименьших квадратов – квадратичная ошибка (формулы (4), (6)). Известно, что бинарная кросс-энтропия имеет пороговое время обучения, при котором она достигает своего насыщения и перестаёт влиять на дальнейшее изменение параметров сетей, тогда как квадратичная функция ошибки даёт постепенно убывающий, но не нулевой вклад в градиенты параметров. Это может означать, что решающий вклад в качество восстановления изображений имеет именно часть функции ошибок, отвечающая за содержание изображения (content loss).

На рис. 6 представлены изображения цифр, восстановленные лучшими генераторами (по метрикам PSNR и SSIM, см. рис. 5), а также целевые изображения цифр и изображения цифр с рамкой. Видно, что оба лучших генератора дают хорошее качество восстановления цифр.

Заключение

В данной работе мы исследовали применение генеративных состязательных сетей для восстановления изображений, получаемых с однопиксельной камеры. В частности, мы сравнили работу двух видов генеративных состязательных сетей – глубокой сверточной генеративной состязательной сети и генеративной состязательной сети наименьших квадратов. Было установлено, что при отсутствии аппаратных искажений генеративная состязательная сеть наименьших квадратов (по сравнению с глубокой сверточной генеративной состязательной сетью) достигает несколько лучшего качества восстановления изображения. Однако при наличии аппаратных искажений глубокая сверточная генеративная состязательная сеть даёт стабильно лучшее качество восстановления изображения по сравнению с генеративной состязательной сетью наименьших квадратов. Мы связываем это с различными свойствами сходимости конкурентных частей функций ошибок двух видов генеративных сетей.

Применение нейронных сетей для задачи однопиксельной визуализации является перспективным и новым направлением. Хотя успешность использования нейронных сетей в однопиксельной визуализации уже продемонстрирована в работах последних лет, область содержит множество направлений для исследований. Во-первых, по мере развития алгоритмов глубокого обучения возникают всё более эффективные подходы к решению различных задач (например, генерации изображений и улучшения их качества). Поэтому использование и оценка возникающих новых нейросетевых алгоритмов для задачи однопиксельной визуализации представляет собой отдельное направление работ. Во-вторых, поскольку целью развития однопиксельной визуализации является создание новых устройств, позволяющих получать изображения объектов в условиях, недоступных традиционным многопиксельным камерам, важно учитывать требования к производительности нейросетевых алгоритмов с прикладной точки зрения. Поиск баланса между качеством получаемых изображений и накладными расходами – временными затратами на обучение и объемом памяти, необходимым для запуска программных приложений, обеспечивающих восста новление изображения, – представляет собой отдель ное направление будущих исследований.

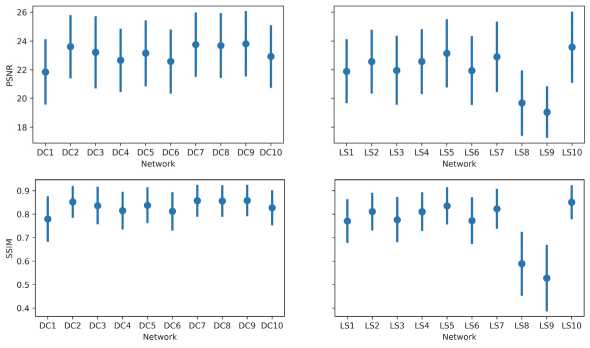
Рис. 5. Значения метрик PSNR и SSIM для 10 различных генераторов двух типов, обученных на восстановление изображений с однопиксельной камеры при частоте выборки 8 %. Каждое значение вычислялось на тестовом наборе из 10000 изображений цифр. Обозначение DCN соответствует N-й глубокой сверточной генеративной состязательной сети, а обозначение LSN – N-й генеративной состязательной сети наименьших квадратов

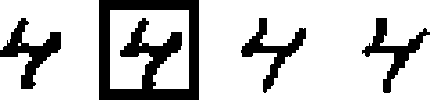
Ground truth               Framed                  DCGAN                  LSGAN

Рис. 6. Примеры изображений цифр, восстановленных с помощью лучших (по метрикам PSNR и SSIM) генераторов (см. рис. 5)

Исследование выполнено за счет гранта Российского научного фонда № 23-22-00381,