Изучение механизма рабочего органа в кузнечно-штамповочном оборудовании

Введение. Статья посвящена исследованию синтезированной принципиальной схемы фрикционного контакта твердых тел в кузнечно-штамповочных машинах. Установлена возможность получения максимума нагрузочной характеристики фрикционного контакта внутри интервала изменения коэффициента трения. Выявлены две следующие возможности сил трения фрикционного контакта: на границах указанного интервала они будут равны при наличии максимума равенства; при данных условиях они достигают наибольшей стабильности.

Материалы и методы. При изменении величины угла меняется положение точки максимума. Это приводит к нарушению равенства сил трения на границах интервала изменения коэффициента трения. В таком случае коэффициент точности должен определяться отношением максимума функции к наименьшему граничному значению. Для этого необходимо установить тенденции изменения граничных значений функции, связанные с варьированием величины угла. Для решения этой задачи новую величину тангенса угла давления представили в виде произведения коэффициента варьирования на базовое значение тангенса угла.

Результаты исследования . Полученные результаты показывают высокую стабильность силы трения при проскальзывании тел фрикционного контакта (ФК). Однако при больших величинах угла давления чувствительных элементов датчика-преобразователя максимальная сила трения кратковременно может быть пропорциональна текущему значению коэффициента трения.

Обсуждение и заключения . Модернизированная принципиальная схема ФК позволяет теоретически получить очень высокую стабильность силы трения. ФК не должен обращаться в ноль в интервале изменения коэффициента трения выходного параметра основной фрикционной группы (ОФГ) и при наличии максимума функции нагрузочной способности ФК. Необходимым условием этого является передача чувствительными элементами дополнительной фрикционной группы (ДФГ) ее полной нагрузки.

Introduction. The synthesized basic diagram of the frictional contact of solids in forging-and-stamping machines is considered. The possibility of obtaining the maximum load characteristics of the frictional contact within the variation interval of the friction factor is determined. The following two possibilities of frictional contact forces are indicated: they will be equal at the boundaries of the specified interval if there is maximum balance; they achieve the greatest stability under these conditions.

Research Results. The results show high stability of the friction force under slipping of the frictional contact (FC) bodies. However, at large values of the pressure angle of sensing elements of the transducer, the maximum friction force can be for a short moment proportional to the current value of the friction factor.

Discussion and Conclusions. The upgraded FC basic diagram enables to theoretically obtain very high stability of the friction force. The FC should not vanish within the variation interval of the friction factor of the output parameter of the basic friction group (BFG) and at the maximum of function of the FC load capacity. A necessary condition for that is the transfer of full capacity of the additional friction group (AFG) by the sensing elements.

Образец для цитирования: Кобзев, К. О. Изучение механизма рабочего органа в кузнечно-штамповочном оборудовании / К. О. Кобзев // Вестник Дон. гос. техн. ун-та. — 2019. — Т. 19, № 2. — С. 158-163.

Введение. Исследована синтезированная принципиальная схема фрикционного контакта (ФК) твердых тел в кузнечно-штамповочных машинах. В результате анализа установлена возможность получения максимума нагрузочной характеристики ФК внутри интервала изменения коэффициента трения. Выявлены две следующие возможности сил трения фрикционного контакта: на границах указанного интервала они будут равны при наличии максимума равенства; при данных условиях они достигают наибольшей стабильности.

Полученные результаты показывают высокую стабильность силы трения при проскальзывании тел ФК. Однако при больших величинах угла давления чувствительных элементов датчика-преобразователя максимальная сила трения кратковременно может быть пропорциональна текущему значению коэффициента трения.

Материалы и методы. Указанного недостатка лишена схема ФК, приведенная на рис. 1.

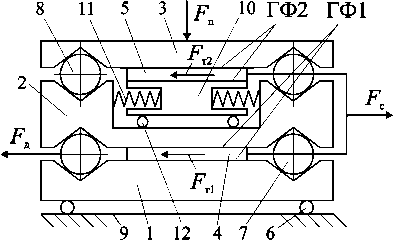
Рис. 1. Принципиальная схема фрикционного контакта

Основную фрикционную группу ГФ1 составляют тела 1, 2 и 4; дополнительную фрикционную группу ГФ2 — тела 3, 5 и 10. Между телами 1 и 2, 2 и 3 размещены в профилированных гнездах чувствительные элементы в виде тел качения 7 и 8.

Отличием рассматриваемой схемы является разделение тела 2 на две части, благодаря чему связь между телами 2 и 5 осуществляется посредством тела 10, взаимодействующего с телом 2 через пружины 11. Это позволяет передавать половину общей нагрузки ГФ2 от тела 2 непосредственно на тела качения 8, сделав их ведущим элементом в составе ГФ2. Вторая половина общей нагрузки ГФ2 передается за счет пружин 11 от тела 2 телу 10 и далее посредством трения — телу 5. Кроме того, место приложения движущей силы Fд перенесено с тела 1 на тела качения 7. Указанные отличия позволяют исключить влияние величины угла давления тел качения 7 на распределение нагрузки между поверхностями трения в ГФ1 и ГФ2 при изменении величины коэффициента трения [1].

Для сведения к линейному характеру трения между телами 1 и опорной поверхностью 9, а также между телами 2 и 10 установлены катки 6 и 12.

Формула для определения величины силы трения ФК в зависимости от возмущающего воздействия имеет следующий вид (при одинаковых значениях коэффициента усиления обратной связи ГФ1 и ГФ2):

Z F t =

4 F п f

(1+ ft g a )²

где ZFt — суммарная предельная сила трения между телами 1, 2, 4 и 3, 5, 10; F — начальное усилие замы кания фрикционных пар; f — текущее значение коэффициента трения между упомянутыми телами; a — угол давления между телами качения 7, 8 и гнездом.

Установлено также, что функция (1) внутри интервала значений f min ... f max не имеет максимума, так как сила трения ГФ1 обращается в нуль при значении коэффициента трения f_о = 1/ tg a . (Здесь f min и f max — соответственно наименьшее и наибольшее значения, которые может принимать коэффициент трения в реаль-

Машиностроение и машиноведение

ных условиях эксплуатации ФК для принятого сочетания материалов фрикционных пар.) Это же значение соответствует мнимому максимуму функции (1), поскольку в интервале f _о... f _max нагрузка ФК передается фрикционной группой ГФ2, сила трения которой возрастает с увеличением f . Это не обеспечивает стабильность силы трения ФК, несмотря на то, что она несколько выше, чем у ФК первого поколения (при значениях f min = 0,1, f max = 0,8 и tg a = 1,125 коэффициент точности соответственно равен K _т = 2,5 и K _т = 3,67).

Реальный максимум нагрузочной характеристики ФК внутри интервала изменения возмущающего воздействия возможен путем видоизменения ГФ2 согласно схеме (см. рис. 1). Данное видоизменение заключается в уменьшении числа фрикционных пар. Для этого из схемы необходимо исключить элементы 10, 11 и опереть тело 5 непосредственно на тело 2 через катки 12.

В соответствии с этим найдем:

F2 = (F - Fp2 ) f, где Fт2 — сила трения ГФ2; Fр2 — управляющее воздействие ГФ2 (распорная сила на телах качения 8).

Но

^F p2 = ^F t2 tg a ,

Поэтому

F T 2 =

F п f .

1+ f tg a .

Сила трения между парами ГФ1 равна:

F t1 = 2 F -I 2 +

^F t2 I tg ^a f .

Учитывая соотношение (2), найдем

Ft1 = 2 Fп

f

(1+ f tg a )² .

Соотношение (3) не содержит разности в числителе, поэтому данная функция ни при каких условиях не обращается в нуль. Она лишь асимптотически приближается к нулю при следующих условиях: — теоретически неограниченное возрастание коэффициента трения;

— максимум в точке, соответствующей значению /_к = 1/ tg a [2-5].

Суммируя силы трения по соотношениям (2) и (3), получим

£ F = Ff ^{3 +} ft^ga .

(1+ f t g a )²

Продифференцировав функцию (4) по аргументу f и приравняв нулю производную, найдем значение коэффициента трения, соответствующее максимуму функции:

f< = — tg a

.

Подставив в выражение (4) последовательно значения f min , f max и приравняв друг другу полученные соотношения, найдем:

(m+1)+ (m+1)2 +12m tga =------—---------.                                   (6)

• 2    f max

Здесь m — относительная ширина интервала изменения коэффициента трения: m = f max / f mn .

При найденной величине tg a функция (6), имея максимум в точке, соответствующей значению (5), принимает одинаковые значения на границах интервала изменения коэффициента трения.

Коэффициент точности в этом случае определяется отношением максимума функции (4) к ее любому граничному значению (при значениях f min или f max ). На основании этого получим:

9(1+ f max tg a )²

.

K т =-----------------

8 fmaxtga(3 + fmax tga)

Установим значение параметра tga, при котором величина Kт минимальна. При изменении величины tga изменяется положение точки максимума f к . Только соотношение (6) устанавливает равенство сил трения на границах интервала изменения f , поэтому изменение положения точки максимума функции (4) приводит к нарушению упомянутого равенства. В таком случае коэффициент точности должен определяться отношением максимума функции (4) к наименьшему граничному значению. Для этого необходимо установить тенденции изменения граничных значений функции (4), связанные с варьированием величины tga [6-10].

Для решения данной задачи представим новую величину тангенса угла давления в виде произведения коэффициента варьирования K и базового значения тангенса угла в соответствии с выражением (6), т. е.: tg a i = K tg a . (8)

На основании этого можно записать, с учетом (4):

⁽³ m + Kf m _ax ^{tg a )} f max >  (3+ ^Kf _max ^{tg a ) f} max

( m + Kf max tg a )²       (1 + Kf max tg a )²

Здесь левая часть соответствует силе трения ФК при значении f = f min , правая часть — силе трения при значении f = f max . Решение последнего неравенства относительно коэффициента варьирования имеет вид:

K е -да;

( m + 1) - ( m + 1)² + 12 m ² f max tg ^a

и (1;

+ да).

Так как tga >0, дробь в скобках левой части решения отрицательная, поэтому при K >1 составленное неравенство, безусловно, выполняется, т. е. при смещении точки максимума fк в область меньших значений для вычисления коэффициента точности необходимо использовать величину силы трения ФК, соответствующую значению f max, и, наоборот, при 1> K >0 необходимо принимать величину силы трения, соответствующую значению fmin [11-13].

Используя данный вывод, составим неравенство вида K _т 1 >  K _т, где K _т 1 — коэффициент точности, вычисленный с учетом равенства (8). Имеем:

(1 + Kf _n ax tg a )² _? (1+ f _n ax tg a )² .

K (3+Kfmax tga)   3 + fmax tga "

Неравенство составлено с учетом того, что K >1. Преобразование полученного неравенства к виду

• 3    + (1 + K)f maxtga + Kf 2maxtg2a > 0

показывает справедливость предположения о том, что K _т 1 >  K _т.

Исследуем соотношение величин коэффициентов точности при смещении точки максимума функции

• (4)    в область больших значений, т. е. при K <1. Тогда K _т 2 >  K _т, или

• ( m + Kfmaxtga)2 J1'fmaxtga)2

K (3 m +Kfmaxtga)   3 + fmaxtga

Преобразование составленного неравенства к виду

• 3m + (m + К)f maxtga - Kf 2maxtg2a > 0

и решение последнего дает

K <    ^{m (3+ f} max tg ^{a )}

f max ^t g ^{a- 1) f} max tg ^{a .}

Дробь в правой части полученного решения равна единице при значении

(m+1 )+^( m+1)2+12 m что полностью соответствует решению (6). Следовательно, неравенство Kт2 > Kт выполняется в случае, если K <1.

Результаты исследования. Примем окончательное суждение о стабильности силы трения ФК при различных формах нагрузочной характеристики. Для этого определим коэффициент точности ФК, когда функция (4) имеет максимум при значении f = f _max. В этом случае функция монотонно возрастает в интервале изменения коэффициента трения. При этом справедливо равенство f max = 3/ tg a . Получим:

Машиностроение и машиноведение

_К     ^{Z F} T( f max )    ⁽ m + ^{3) 2}

• т³ " Z F m( f min ) "  8( m + 1).

Учитывая K _т з >  K _т, найдем:

• ³ m ⁽ 3 - mf max tg a ) + m ⁽ 3 - m ) f 2 _maxtg 2 a + 9 ⁽ 1 - f _naxtg a ) < 0.

Для всех фрикционных материалов, применяемых в качестве пар трения ФК, m >3. Согласно (6), f _naxtg a> 1, поэтому очевидно, что разности в скобках полученного неравенства отрицательные и сделанное выше предположение справедливо.

Таким образом, проведенный анализ показывает, что наибольшая стабильность выходного параметра ФК будет в том случае, когда функция (4) имеет максимум внутри интервала изменения коэффициента трения и принимает одинаковые значения на его границах.

При m = 8 и f _nax = 0,8 получим tg a« 14. Тогда f _к « 0,214. В этом случае максимум функции (3) будет при значении f к « 0,071, что практически идентично нижней границе интервала f = f _n i _n = 0,1. Функция (3) убывает внутри интервала изменения коэффициента трения. При таких исходных параметрах K _т « 1,04, а K _т3 « 1,68.

Обсуждение и заключения. Как видим, модернизированная принципиальная схема ФК позволяет теоретически получить очень высокую стабильность силы трения. Однако вследствие относительно большого значения параметра tg a усилие F_п используется неэффективно. ФК не должен обращаться в ноль в интервале изменения коэффициента трения выходного параметра основной фрикционной группы (ОФГ) и при наличии максимума функции нагрузочной способности ФК. Необходимым условием этого является передача чувствительными элементами дополнительной фрикционной группы ДФГ ее полной нагрузки. Дополнительное условие существования максимума можно сформулировать следующим образом: при равном числе пар трения обеих фрикционных групп чувствительные элементы ОФГ передают часть ее полной нагрузки; при меньшем, чем в ДФГ, числе пар трения чувствительные элементы передают полную нагрузку ОФГ.