Изучение процессов распространения информации в социальной сети видеохостинга Youtube

Дидоренко А. В., Прогулова Т. Б. Изучение процессов распространения информации в социальной сети видеохостинга YouTube // Системный анализ в науке и образовании: сетевое научное издание. 2023. № 2. С. 1-20. EDN: SEKZE. URL :

Феномен распространения играет важную роль в реальном мире; его изучение направлено на создание строгой аналитической и численной платформы для количественной оценки и прогнозирования распространения, например, вредоносного программного обеспечения в Интернете, слухов, новостей, коммерческой и социальной рекламы, каскадных сбоев в электронных схемах, вирусов в популяции и т. д. [1]. Доскональное их понимание имеет важное значение для контроля и использования динамики распространения в различных областях.

Многие социальные, физические и биологические системы могут быть хорошо описаны сложной сетью, где узлы представляют некие сущности, а связи — взаимодействия между парами сущностей. В последние годы было доказано, что сложно-сетевой подход является ценным и эффективным инструментом для описания поведения и взаимодействия между индивидами. Большей частью коллективные формы поведения распространяются через социальные контакты. От возникновения социальных норм до принятия технологических инноваций и роста социальных и политических движений социальные сети являются путями, которыми происходит распространение. Исследования динамики распространения показали, что структура (или топология) социальной сети может иметь серьезные, и даже решающие последствия для возникающих паттернов коллективного поведения. Поэтому методы теории сложных сетей привлекли внимание ученых, изучающих феномены распространения [2].

В наше время одной из самых мощных сред распространения информации стала сеть Интернет, которая породила множество разнообразных онлайн-платформ и онлайн-социальных сетей, заточенных на обмен информацией. Одна из таких платформ – видеохостинг YouTube , включающий в себя онлайн-социальную сеть. За последние несколько лет YouTube превратился в совершенный ресурс обмена разного рода информацией. Функционирование видеохостинга привлекает внимание как обыкновенных пользователей, так и организаций. Интригующей остаётся роль YouTube как информационного оружия в избирательных компаниях, брекзите, формировании общественного мнения или заговоров, и многом другом. Все вышеперечисленные процессы на уровне каналов протекают с учетом структуры сети подписок, но под управлением системы рекомендаций, принцип работы которой в целом не известен.

Попытки понять и смоделировать явления распространения предпринимаются с 1920-х годов. Систематическое изучение процессов распространения началось с моделирования распространения болезней в популяции, которое было сложной задачей из-за отсутствия деталей того, «кто кого заразил». Детальная информация такого рода и сейчас, как правило, является проблемой, однако развитие технологий сбора и накопления данных привело к тому, что в настоящее время результаты наблюдений или экспериментов, связанных с распространением информации (или патогенов) доступны на специальных репозиториях в сети Интернет. Анализ этих данных позволяет разрабатывать более реалистичные модели распространения [3].

В рамках данной работы проведено исследование влияния структурных особенностей социальной сети видеохостинга YouTube на процессы распространения информации. YouTube был представлен как сеть, где узлами выступили YouTube -каналы, а связи описывали отношения подписки между каналами.

Метод исследования

Видеохостинг YouTube включает в себя гигантскую социальную сеть, - её исследование возможно только на уровне подсетей. Полная сеть YouTube доступна только Google / YouTube , а данные для видео доступны только через специальные функции. В данной работе структура сети YouTube представлена следующим образом: узлам соответствовали YouTube -каналы, а направленным связям -отношения подписки между каналами.

Для исследования были построены выборки-подсети с использованием API общедоступных данных Google / YouTube с последующим извлечением сетевых данных. Важно отметить, что многие свойства сетей могут быть выявлены из особенности распределения степеней, поэтому всё исследование проводилось на трёх сетях: эмпирическая сеть, рандомизированная с сохранением распределения степеней эмпирическая сеть и случайная сеть Эрдёша–Реньи с тем же количеством узлов и связей.

Для построенных сетей вычислялись основные глобальные и локальные характеристики. Для выявления структурных особенностей всех сетей определялись структуры сообществ и ядро-периферия, класс сети, показатель предпочтительного присоединения и характер корреляций степеней узлов.

С учетом выявленных свойств была определена модель распространения, позволяющая имитировать процессы в сетях. Изучалось влияние структуры сообществ на распространение, а также влияние выбора значимых (центральных) вершин в качестве источников распространения на максимизацию охвата сети.

Построение выборки

В качестве эмпирической сети была выбрана сеть YouTube - каналов новостного характера, так как процессы распространения информации лучше всего изучать на том сегменте, где рассылка информации протекает активнее всего, а именно в СМИ.

В настоящем исследовании сбор данных был начат от 100 самых больших по числу подписчиков новостных YouTube -каналов [4]. К ним, например, относится индийский новостной канал на языке хинди, принадлежащий TV Today Network «Aaj Tak» (57.5 млн подписчиков), а также южнокорейский новостной канал «MBCNEWS » (3.45 млн подписчиков). Процедура сбора данных описана в [5].

Необходимо отметить, что процесс сбора данных производился по подпискам просматриваемых каналов, поэтому полученный список рёбер отражает ситуацию, когда один канал подписан на другой. Если рассматривать эту структуру данных с точки зрения распространения информации, то её оригинальный вид не позволил бы моделировать процессы распространения адекватно. Дело в том, что когда исходный канал публикует видеоролик, то эту публикацию могут увидеть в разделе рекомендаций те каналы, которые подписаны на него (являются подписчиками), а не каналы, на которые он подписан (если только не существует взаимной подписки). Поэтому для моделирования распространения информации список рёбер был инвертирован, то есть для каждого направленного ребра просто было изменено направление.

После сбора данных построение и анализ сети YouTube - каналов проводились в среде RStudio , посредством языка статистического программирования R с использованием библиотеки анализа сложных сетей igraph .

Анализ структуры сети YouTube – каналов

Для построенной сети YouTube -каналов определялись основные характеристики сети, распределение степеней (и его показатель), показатель нелинейности предпочтительного присоединения, характер корреляций степеней вершин, коэффициент кластеризации, значения центральностей вершин и их распределения, структуры сообществ и ядро-периферия. Методика проведения анализа структуры сети частично описана в работе [5].

Основные характеристики эмпирической сети представлены в табл. 1.

Табл. 1. Основные характеристики построенной сети

Характеристика	Значение
Количество узлов	13604
Количество связей	123344
Направленная сеть	Да
Диаметр	19
Радиус	1
Среднее расстояние	5.6
Коэффициент кластеризации	0.074
Коэффициент кластеризации случайной сети аналогичного размера	0.0014
Средняя степень	18.13
Средняя полустепень захода/исхода	9.06

Таким образом, для сети новостных каналов в YouTube характерно небольшое среднее расстояние. Значение коэффициента кластеризации, на первый взгляд, не велико – 0.074, но коэффициент кластеризации для случайной сети Эрдёша-Реньи с тем же количеством вершин и ребер (или при рандомизации исходного графа) равен 0.0014 (почти в 53 раза меньше). Это говорит о существенной кластеризации сети каналов YouTube .

Распределения степеней анализируемой сети показаны на рис. 1.

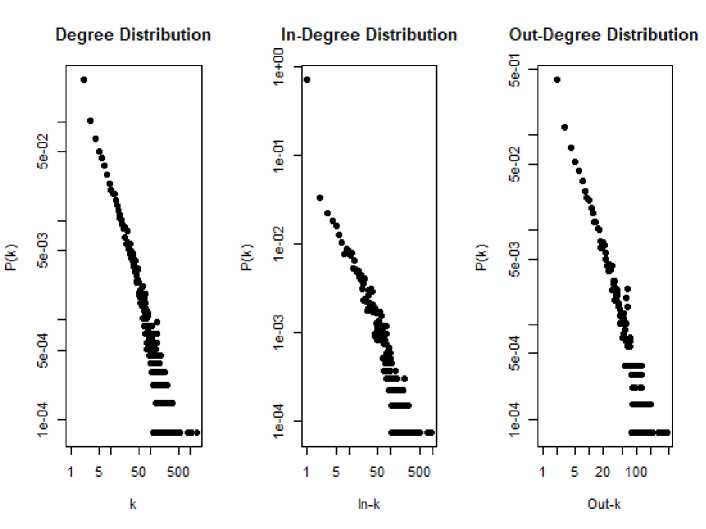
Рис. 1. Распределение степеней, полустепеней захода и исхода новостной сети в log-log масштабе

Форма распределений указывает на то, что изучаемая сеть является масштабно-инвариантной. Для вычисления показателя распределения степеней проводилась аппроксимация распределения степенной функцией Р(к)~ к~^Y методом максимального правдоподобия. Для оценки показателя степенного распределения использовалась формула [6]:

У=1 + п[Я* = Jn^] "' , ^L          к-тигн

где у - оценка показателя степени, n - число узлов в сети, к_тi_n - минимальная степень, к ; - степень i -го узла. Результаты показали, что значение показателя при минимальной степени, равной 16, близко к 2, а именно 2.01±0.02. Таким образом, распределение степеней изучаемой сети YouTube - каналов описывается степенным законом Р(/с)~к^-у с показателем степени у « 2.01 ± 0.02.

Для определения значения показателя предпочтительного присоединения использовалась методика, описанная в [5]. Вычислялась кумулятивная зависимость интенсивности изменения степени вершин, представленная на рисунке 2. Синие точки соответствует полученной зависимости, а оранжевая прямая - зависимости в случае линейного предпочтительного присоединения. Сравнение указывает на подлинейное предпочтительное присоединение в эмпирической сети с показателем степени, равным ~0.7 [1]. Нелинейность предпочтительного присоединения указывает на дополнительные механизмы, влияющие на эволюцию сети, такие как удаление вершин и рёбер, ускоренный рост, структурное старение и т.д. Поэтому определение показателя предпочтительного присоединения является очень существенным для описания эволюции сетевых систем.

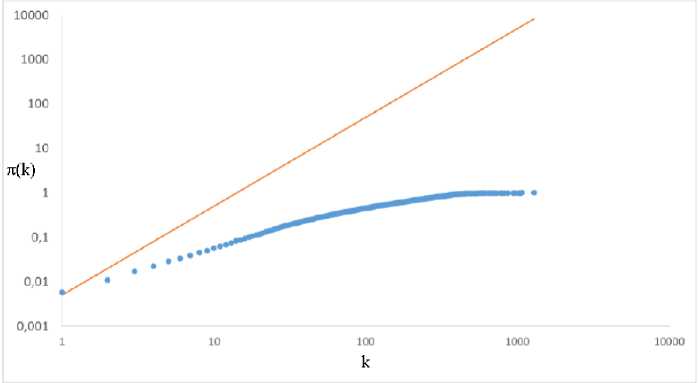
Рис. 2. Зависимость ( ) , вычисленная для фрагмента сети каналов YouTube. Синие точки соответствуют эмпирической зависимости, прямая линия – оценочная – соответствует значению показателя предпочтительного присоединения = 1

Далее проводилась к - ядерная декомпозиция эмпирической сети для определения структуры ядро-периферия. к -оболочку ( к-shell) графа можно определить, как максимальный связный подграф графа G , котором каждый узел имеет степень не менее к [3]. Узлы, которые попали в к -оболочку, формируют так называемое к- ядро ( к-core ) сети. Таким образом, в терминах к -оболочек сеть описывается слоистой структурой (похожей на структуру луковицы), раскрывающей полную иерархию её узлов (см. рис. 3). k- ядро, соответствующее максимальному значению k , называют ядром сети, в то время как остальные узлы формируют периферию сети.

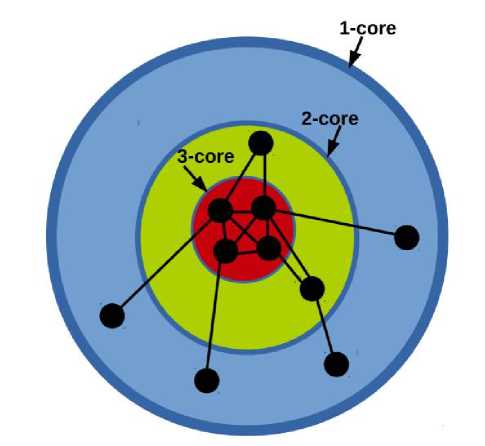
Рис. 3. Структура «ядро-периферия»: Узлы 3- ядра являются узлами ядра сети, а все остальные – узлами периферии

На рис. 4 показано распределение полученных значений показателя k-shell в log-log - масштабе для ненаправленной сети. Из распределений видно, что подавляющее большинство узлов имеют небольшие значения k-shell. Максимальное значение k-shell , равное 64, имеют 66 вершин. Такая картина позволяет говорить о том, что эмпирическая сеть обладает структурой ядро-периферия, где ядрами являются вершины с высоким значением k-shell , а остальные вершины являются периферийными.

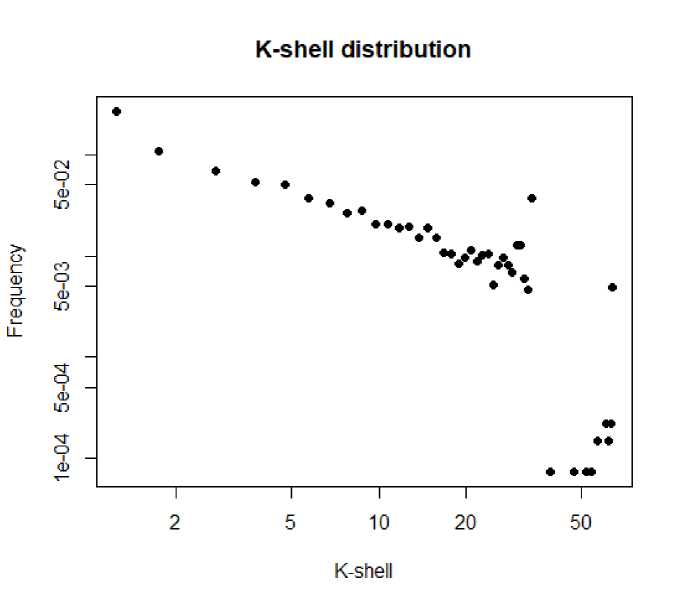
Рис. 4. Распределение значений k-shell эмпирической сети в log-log масштабе

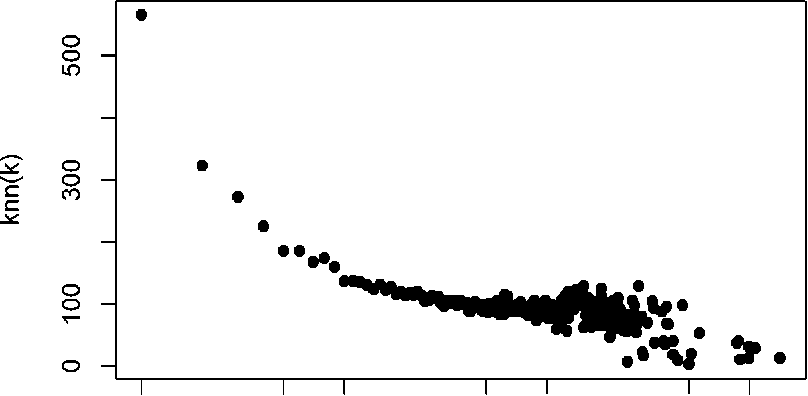
Вычислялся коэффициент ассортативности, отражающий тенденцию узлов сети соединяться с другими узлами, близкими по степени для обнаружения наличия и характера корреляций степеней вершин. Для изучаемой сети коэффициент ассортативности равен - 0․157. На рис. 5 приведена зави- симость средней степени ближайших соседей вершины от её степени (к^^к) для эмпирической сети.

1           5   10         50 100        500

Рис. 5. Зависимость средней степени ближайших соседей вершины от её степени {к _пп} (к) новостной сети

Отрицательное значение коэффициента ассортативности и убывающий характер зависимости указывают на то, что сеть слабо-дисассортативна, то есть вершины с большой степенью имеют тенденцию соединяться с вершинами малой степени и наоборот.

Для понимания того, являются ли корреляции в сети следствием структурной дисассортативно-сти или же генерируются некоторым неизвестным процессом, производилось сравнение (к^^к?) для изучаемой сети и соответствующей рандомизированной c сохранением степеней сети (рис. 6).

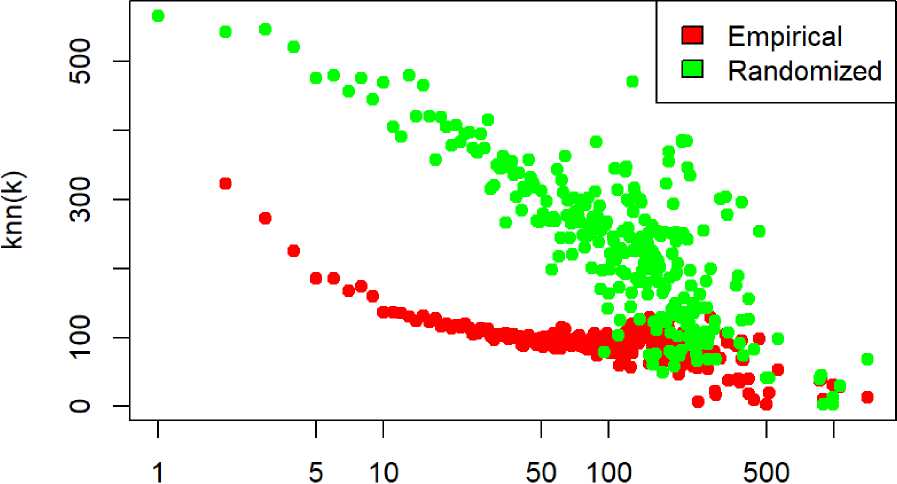
Рис. 6. Зависимость средней степени ближайших соседей вершины от её степени (k^^k). Красные точки соответствует эмпирической сети, а зелёные – рандомизированной сети

Сравнение показывает, что слабая ассортативность в правой части, при больших значениях к при рандомизации исчезает, т. е. она присуща сети, что и является типичным для сетей со структурой сообществ, а дисассортативность при малых k, очевидно, является структурной, индуцированной распределением степеней сети.

В сложно-сетевом анализе и в теории графов для количественной характеристики важности узла в сети водятся показатели центральности , благодаря которым можно выполнять ранжирование узлов по степени значимости. Приложения включают идентификацию наиболее влиятельных сущностей в социальной сети, ключевых узлов инфраструктуры в Интернете или городских сетях и суперраспространителей болезней. Концепции центральности были впервые разработаны в анализе социальных сетей, и многие термины, используемые для измерения центральности, отражают их социологическое происхождение [7].

На следующем шаге анализировались центральности для узлов эмпирической сети, рандомизированной с сохранением степеней эмпирической сети и случайной сети Эрдёша-Реньи аналогичного размера. Вычислялись такие центральности, как:

• -    vertex betweenness - доля кратчайших путей между вершинами графа, которые проходят через эту вершину [1];

• -    eigenvector - значения центральности каждого узла пропорциональна сумме центральностей тех узлов, с которыми он связан [8];

• -    pagerank - модификация eigenvector , учитывающая направление связей в графе [9];

• -    hub score - показатель центральности, означающий, что узел может иметь высокое значение хаба, если он ссылается на большое число узлов с высоким значением авторитета [10];

• -    authority - обратный случай hub score : узел имеет большое значение авторитета, если на него ссылается большое число узлов с высоким значением хаба [10];

• -    closeness - обратная сумма расстояний от узла до всех других узлов графа [11, 12].

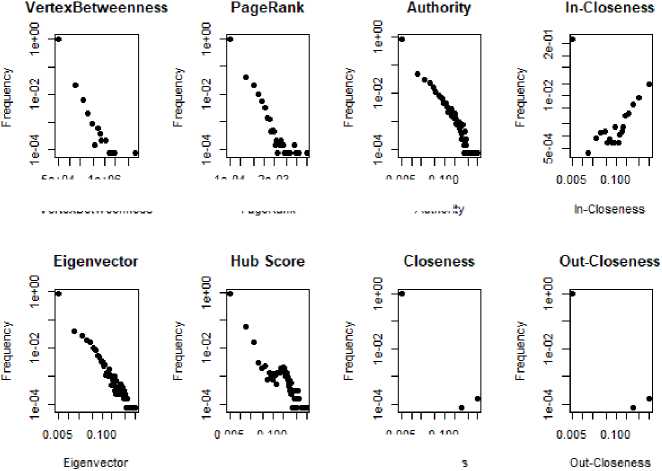
Так как сети являются ориентированными, то центральность closeness вычислялась не только по полным связям, но и по связям захода и исхода. На рис. 7-9 изображены распределения для каждой центральности в случае эмпирической, рандомизированной и случайной сетей, все графики представлены в log-log масштабе. Стоит отметить, что распределения всех центральностей для эмпирической и рандомизированной сетей очень неоднородны (описываются законом, близким к степенному, см. рис. 7-8), в то время как распределения для случайной сети близки к пуассоновскому, как и распределение степеней (см. рис. 9). Характер распределений для эмпирической и рандомизированной сетей позволяет утверждать, что для большей части узлов значения центральностей невелики, узлов с высокими значениями не так много, и можно предполагать, что именно они оказывают наибольшее влияние на сеть. Отдельно стоит отметить, что в рандомизированной сети с сохранением степеней (при стирании структуры сообществ) формы распределений некоторых центральностей меняются. Так, например, в эмпирической сети наблюдается несколько вершин с высоким значением vertex betweenness , в то время как в рандомизированной сети всего одна вершина. Распределения для центральности pagerank различаются по форме и диапазону значений. В случае случайной сети пуассоновский закон распределений говорит об однородности: все вершины имеют значения центрально-стей, близкие к среднему.

Можно заключить, что при «стирании» структуры сообществ при рандомизации с сохранением степеней, появляются значимые различия в значениях таких центральностей, как vertex betweenness, pagerank , eigenvector , hub score .

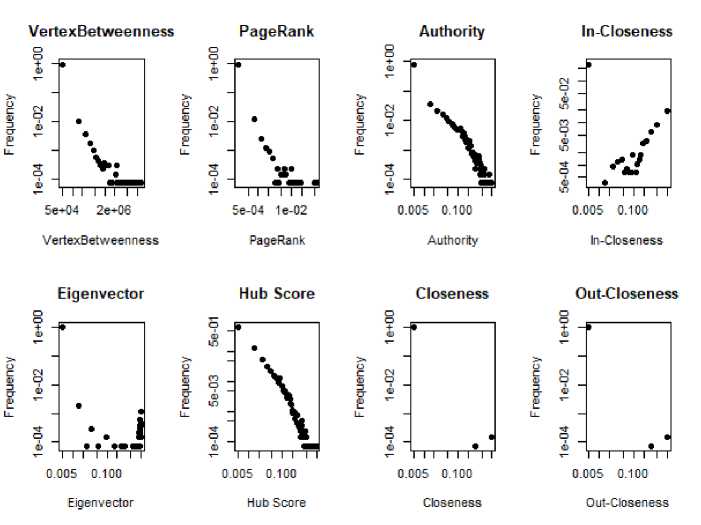
Рис. 7. Распределение центральностей для эмпирической сети

и. 005 0.100

0.005 0.100

Hub Score

Closeness

Рис. 8. Распределение центральностей рандомизированной с сохранением степеней сети

5е+04 1е+оъ

1е-04 2е-оз

0.005 о.юо

VertexBetweenness

PageRank

Authority

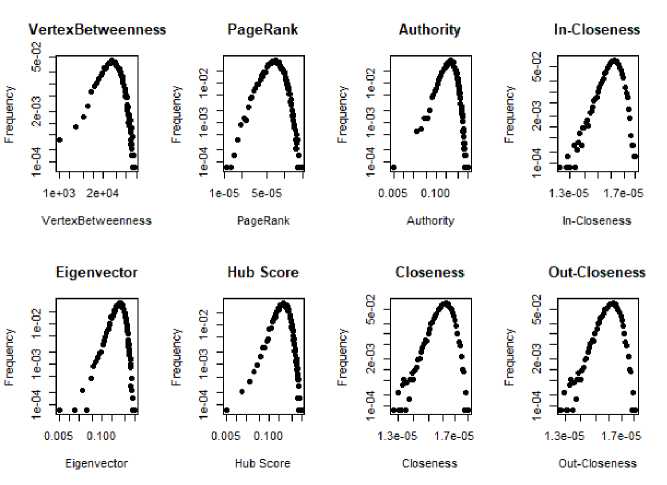
Рис. 9. Распределение центральностей случайной сети Эрдёша-Реньи

Также изучались корреляции значений центральностей. Была построена корреляционная матрица, отражающая коэффициенты корреляции Пирсона между всеми парами характеристик. Результаты для трёх сетей представлены на рис. 10.

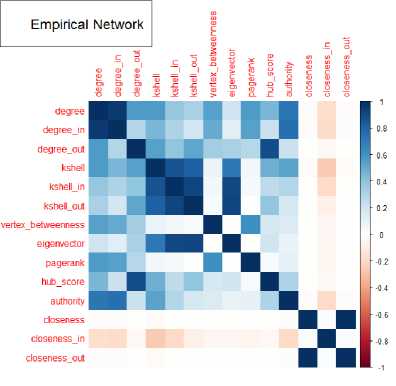
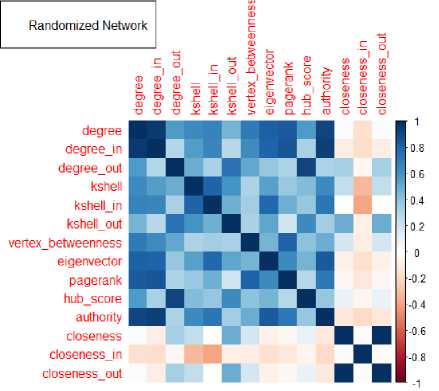
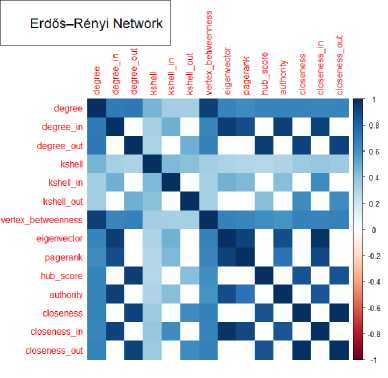
Рис. 10. Матрицы корреляций показателей центральности

Почти все центральности положительно коррелируют между собой (как и со степенями вершин), что объясняет и схожий вид распределения степеней и распределений центральностей. В случае эмпирической сети можно наблюдать слабую отрицательную корреляцию между closeness и другими центральностями. Из корреляционных матриц видно, что при рандомизации сети с сохранением распределения степеней корреляция между некоторыми центральностями усилилась. Например, значения центральности собственного вектора стали сильнее коррелировать со степенями вершин и значениями центральностей pagerank, authority и hub score. Можно предположить, что структура сообществ ослабляет корреляцию (взаимозависимость) значений центральностей узлов. Наконец, матрица корреляций значений центральностей узлов случайной сети Эрдёша-Реньи демонстрирует отсутствие отрицательной корреляции.

Наконец, изучалась структура сообществ в сети YouTube -каналов. Для выделения сообществ использовался алгоритм Louvain, который часто используется на больших графах [13]. Полученные результаты зафиксированы на рис. 11, где отображено значение модульности М, количество найденных сообществ, а также их размеры.

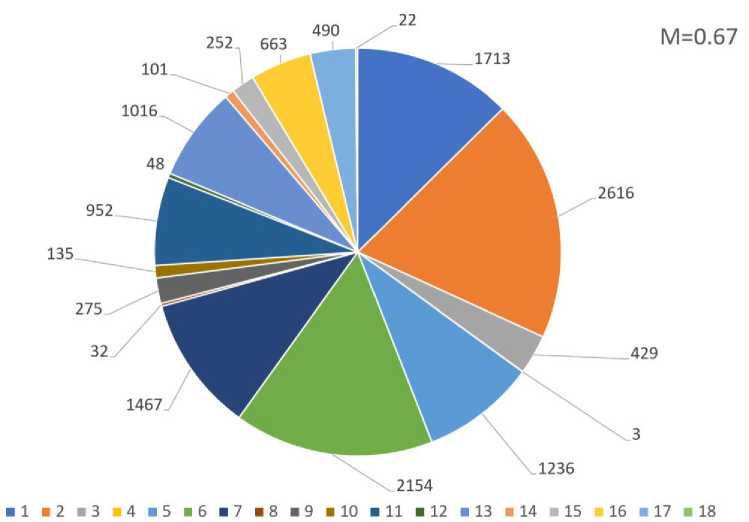
Рис. 11. Результаты поиска сообществ в эмпирической сети

Проведенный анализ сети каналов YouTube позволяет заключить, что эта сеть является масштабно-инвариантной, относится к слабо-дисассортативным (структурно-диссассортативным) и имеет хорошо выраженные структуры сообществ и ядро-периферия. Анализ формы предпочтительного присоединения указывает на то, что оно имеет подлинейный характер. Стоит подчеркнуть, что подобной структурой обладает не только изучаемый сегмент новостной подсети YouTube . Ранее было показано, что другие подсети YouTube обладают аналогичными структурными свойствами [5].

Выявленные свойства изучаемой сети должны быть учтены при изучении процессов распространения информации.

Исследование процессов распространения информации

Прежде чем приступить к изучению процессов распространения информации в социальной сети видеохостинга YouTube , необходимо зафиксировать сценарий распространения информации, который в дальнейшем будет имитироваться.

Пусть некоторый канал (источник) публикует новый видеоролик. Все каналы, которые подписаны на этот канал, смогут увидеть этот новый контент на главной странице YouTube в разделе с рекомендациями. Каналы-подписчики могут посмотреть этот видеоролик и получить некоторую интерес- ную идею из видео. Далее, каналы-подписчики смогут при желании опубликовать уже свои видеоролики, где фигурирует обсуждение полученной ранее идеи, и уже каналы-подписчики этих каналов аналогичным образом могут принять некоторую идею и распространить её далее (или же проигнорировать). Данный процесс сможет продолжаться до тех пор, пока на всём пути распространения будут встречаться каналы-подписчики, готовые передавать идею далее.

Процессы распространения имитировались на эмпирической, рандомизированной с сохранением степеней и случайной сетях. Сложно-сетевая наука показала, что многие свойства (и динамика) сетей обусловлены наличием вершин очень высокой степени (хабов) и масштабно-инвариантным характером распределения степеней [1]. Рандомизированная сеть была получена из эмпирической сети путём случайного пересвязывания вершин сети с сохранением исходного распределения степеней. Хабы оставались хабами. Такая рандомизация ослабляла и стирала структуру сообществ эмпирической сети, уменьшая показатель модульности от 0.67 до 0.2. Случайная сеть Эрдёша–Реньи, которая была создана по размерам эмпирической сети, не имеет структуры сообществ и вообще структурных особенностей; она однородна, в том числе и в смысле распределения степеней. Таким образом, запуск процессов распространения на разных сетях позволит изучить роль структуры сообществ в исследуемых процессах.

Изучение процессов распространения информации начиналось с имитации процессов посредством SIR [14], так как эта модель считается моделью нулевого уровня, с которой начинается изучение процессов распространения. Модель предполагает, что узлы разделены на три множества S , I , R .

• -    S - множество восприимчивых (не осведомленных) узлов. Когда восприимчивый узел вступает в контакт с информированным, он с вероятностью /? переходит во множество информированных (становится осведомленным).

• -    I - множество зараженных узлов. Это узлы, которые были информированы и способны передать информацию другим узлам. С вероятностью у информированный распространитель переходит в состояния глушителя.

• -    R - множество узлов-глушителей (информирован, но не распространяет).

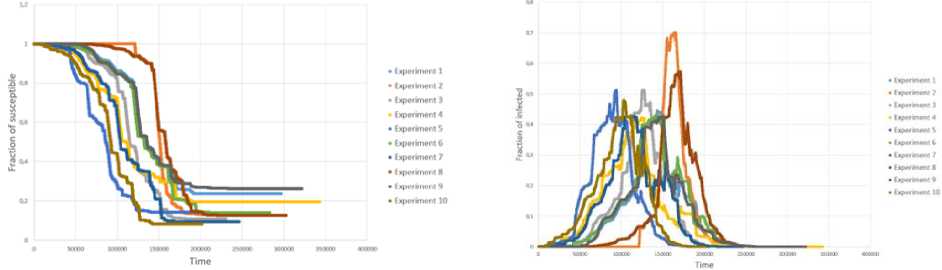
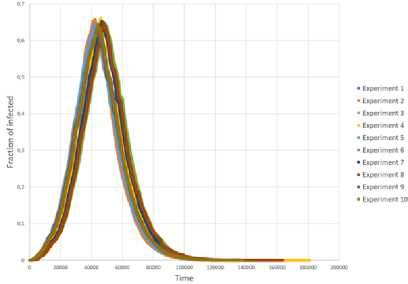
Проводились компьютерные имитации процессов при разных значениях параметров (3 и у, каждый запуск инициировался от случайно выбранной вершины сети. Для случая (3 = 0.8 и у = 0.8 графики, отражающие динамику в 10 запусках процессов показаны на рис. 12-14. Графики показывают, что каждый из 10 процессов, которые проводились на эмпирической сети, имеет приблизительно одинаковую динамику с небольшими различиями, которые могли возникнуть из-за того, что старт производился от разных вершин, а также из-за неоднородности эмпирической сети. В случае рандомизированной и случайной сетей зависимости очень близкие и более гладкие, что может быть связано с большей структурной однородностью этих сетей.

Графики динамики доли неинформированных, информированных и узлов-глушителей на эмпирической сети представлены на рис. 12, для рандомизированной сети - на рисунке 13, а для случайной сети Эрдёша-Реньи - на рис. 14.

S I

R

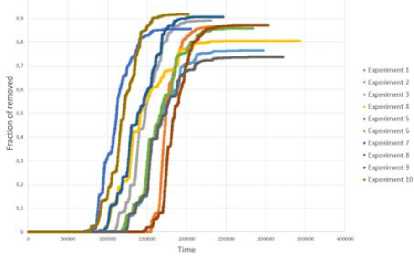
Рис. 12. Динамика доли неинформированных, информированных и узлов-глушителей эмпирической сети

S

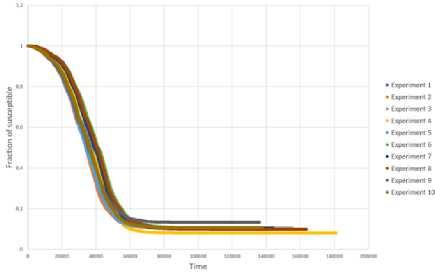
I

R

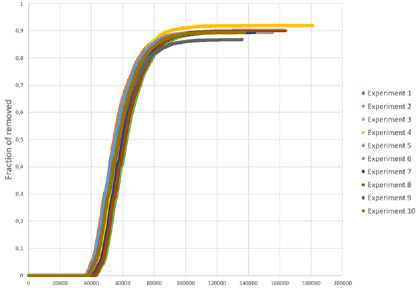
Рис. 13. Динамика доли неинформированных, информированных и узлов-глушителей рандомизированной сети

S

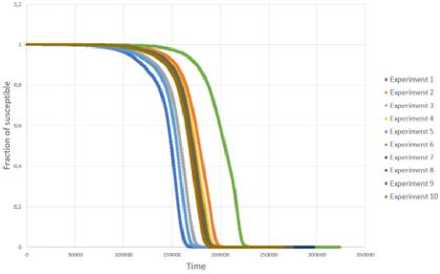
I

R

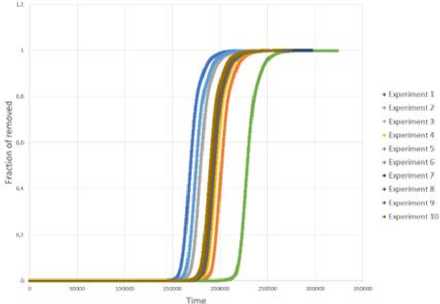
Рис. 14. Динамика доли неинформированных, информированных и узлов-глушителей случайной сети Эрдёша-Реньи

По результатам экспериментов на трёх сетях были получены значения долей неинформированных и узлов-глушителей в стационарном режиме, также фиксировалась максимальная доля информированных узлов и время (количество итераций) выхода процесса распространения в стационарный режим. В табл. 2 приведены усреднённые результаты для всех сетей.

Табл. 2. Усреднённые результаты экспериментов в рамках модели SIR

	Эмпирическая сеть	Рандомизированная сеть	Случайная сеть Эрдёша-Реньи
Доля неинформированных в стационарном режиме	0.15	0.1	0.01
Доля узлов-глушителей в стационарном режиме	0.85	0.9	0.99
Максимальная доля информированных	0.49	0.64	0.83
Время выхода в стационарный режим	269744	147845	276012

Результаты показывают, что в случайной сети процессы в среднем затронули большую часть узлов сети, в эмпирической же сети процессы охватили меньшее количество узлов. Это можно объяснить тем, что в случайной сети отсутствует какая-либо структура, которая могла бы как-то влиять на процессы распространения, поэтому и результаты для этой сети получились более масштабные, чем у эмпирической сети, которая обладает структурой сообществ. Результаты для рандомизированной сети показывают, что процессы распространения охватили большее число узлов за достаточно корот- кое время, по сравнению с эмпирической сетью. Сравнение результатов позволяет предположить, что сообщества выступают в роли «ловушек» при распространении заражения (информации).

Однако стоит учитывать, что модель SIR не подходит для изучения влияния на распространение информации структурных особенностей эмпирической сети, поскольку в ней отсутствует возможность учесть эту структуру. Сообщества в YouTube в основном являются тематически обусловленными [9], естественно предполагать, что вероятность передачи (восприятия) информации между узлами одного сообщества будет больше, чем между узлами, принадлежащими разным сообществам.

Более адекватной моделью распространения информации в социальной сети видеохостинга YouTube является иерархическая каскадная модель распространения на основе связей в сети Edge Based Hierarchical ( EBH) Model , которая учитывает структуры сообществ и ядро-периферия [3]. Согласно этой модели, в момент t = 0 начальные узлы являются активными, а остальные узлы не являются активными. На шаге t + 1 каждый узел, активированный в предыдущий момент t , может активировать своих узлов - соседей в соответствии с иерархией вероятностей, определяемой классом ребра:

РсС >  Рср >  Ррр о >  Ррр ! >  Ррс- ⁽²⁾

Вероятность распространения привязана к каждому ребру Е,, класс ребра зависит от типов обоих смежных узлов, i и j . В модели EBH рёбра разделены на пять классов:

«

={    ∈  : ∈            ∈     } ={    ∈  : ∈            ∈    } ⎪                     ={    ∈  :   ∈            ∈     } ={    ∈  :   ∈            ∈    }: (Ерр о = {еч е Е: ^и = 0}                     .           (3) ={   ∈ :   =1} „ ={ | - узеᴫ с максимальным значением  } ⎪                                     =  / - логическая переменная,

⎩отвечающая за принадлежность узлов и к одному сообществу

Так, индекс « c » означает принадлежность узла ядру сети, а индекс « p » - периферии сети. Рёбра, где оба узла являются периферийными, делятся на два подмножества: если оба инцидентных ребру узла содержатся в одном сообществе, то класс имеет метку 0, иначе 1.

Распространение заканчивается в то время, когда не было активировано ни одного нового узла, и множество, содержащее все узлы, которые были активированы ранее, является конечным результатом процесса распространения [3].

Процессы распространения изучались в рамках EBH -модели опять-таки на эмпирической, рандомизированной с сохранением степеней и случайной сетях, чтобы была возможность различить влияние особенностей структуры и влияние особенностей топологии (масштабно-инвариантный характер распределения степеней). В эмпирической и рандомизированной сетях каждому ребру были установлены вероятности передачи информации по рёбрам, исходя из класса ребра (3) в иерархии вероятностей (2). Была проделана серия экспериментов, ниже приведены достаточно типичные результаты. Для эмпирической и рандомизированной сетей здесь зафиксирована следующая иерархия вероятностей для рёбер: 0.9 > 0.7 > 0.5 > 0.3 > 0.1. Применить аналогичную иерархию для случайной сети не предоставляется возможным ввиду отсутствия у случайной сети структуры сообществ. Поэтому для случайной сети была взята вероятность, которая является средней по всем рёбрам эмпирической сети. Таким образом, для всех рёбер было установлено значение 0.454, определяющее вероятность передачи информации через любое ребро случайной сети.

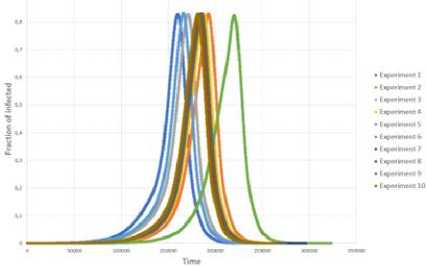
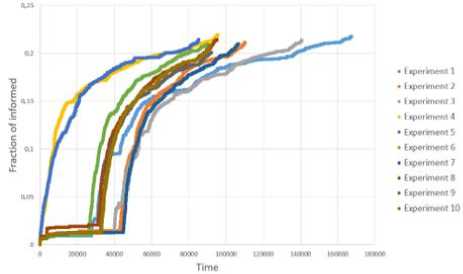
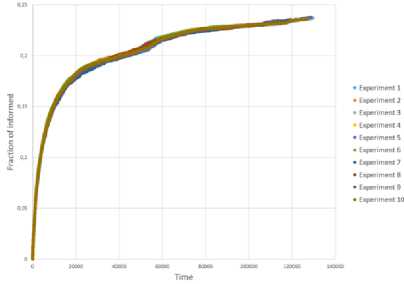
Для имитации процессов распространения информации было произведено по 10 запусков от случайной вершины на всех сетях. На рис. 15 показана динамика доли информированных узлов на каждом запуске. Из графиков также видны некоторые различия в динамике, которые могли быть индуцированы разными стартовыми вершинами.

a

b

c

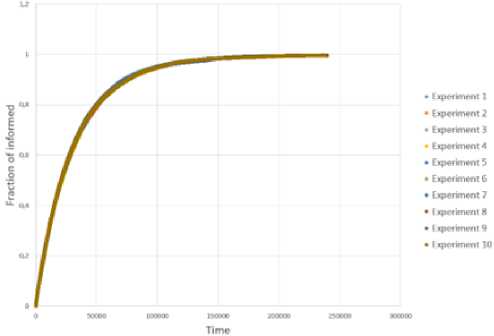
Рис. 15. Динамика доли информированных узлов эмпирической сети (a), рандомизированной сети (b) и случайной сети Эрдёша-Реньи (c)

После 10 экспериментов на всех сетях были получены результаты с финальной долей информированных узлов, зафиксировано финальное время процессов распространения (время выхода в стационарный режим). В табл. 3 приведены усреднённые результаты для всех сетей.

Табл. 3. Усреднённые результаты экспериментов применения модели EBH

	Эмпирическая сеть	Рандомизированная сеть	Случайная сеть Эрдёша-Реньи
Доля информированных в стационарном режиме	0.21	0.24	0.99
Время выхода в стационарный режим	107451	124840	237370

Из таблицы видно, что в случайной сети процессы в среднем охватили почти все узлы сети, в эмпирической же сети процессы охватили меньшее половины узлов. Результаты в случае рандомизированной сети показывают, что информационный охват здесь больше, чем в эмпирической. Как и в случае модели SIR , такие результаты позволяют сделать вывод, что структура сообществ влияет на охват узлов, уменьшая его.

На следующем этапе были произведены попытки максимизации охвата и минимизации времени в процессах распространения. Для этого была проведена серия экспериментов с запуском процессов от вершин с максимальными значениями ранее полученных центральностей, а также от случайных вершин первых трёх оболочек с максимальными значениями k-shell . Симуляции проводились на всех сетях в рамках моделей SIR и EBH (см. табл. 4–5).

Табл. 4. Результаты экспериментов в случае старта от центральных вершин (эмпирическая и рандомизированная сети)

	Эмпирическая сеть						Рандомизированная сеть
	EBH Model		SIR Model				EBH Model		SIR Model
	Охват	Время	S	^max	R	Время	Охват	Время	S	^max	R	Время
Hub	0.21	99344	0.13	0.63	0.87	299641	0.24	124840	0.08	0.67	0.92	133240
Hub in	0.21	923453	0.12	0.61	0.88	239526	0.24	124452	0.08	0.65	0.92	139309
Hub out	0.22	90466	0.11	0.67	0.89	242845	0.24	124798	0.1	0.68	0.9	130021
K-shell	0.22	99245	0.12	0.65	0.88	243098	0.24	124091	0.1	0.7	0.9	134905
K-shell in	0.21	95723	0.14	0.63	0.86	230345	0.24	123999	0.09	0.7	0.91	132093
K-shell out	0.21	91094	0.14	0.61	0.86	235603	0.24	124012	0.09	0.68	0.91	133490
PageRank	0.21	99300	0.12	0.62	0.88	289341	0.24	123983	0.08	0.7	0.92	132987
Eigenvector	0.21	84933	0.15	0.54	0.85	229027	0.24	124987	0.1	0.7	0.9	139942
Closeness	0.21	984562	0.1	0.5	0.9	259541	0.24	125945	0.1	0.69	0.9	138903
Closeness in	0.22	942782	0.1	0.57	0.9	259045	0.24	124094	0.11	0.7	0.89	136343
Closeness out	0.21	856736	0.09	0.05	0.91	213101	0.24	125934	0.08	0.7	0.92	135908
Authority	0.21	87143	0.13	0.53	0.87	230885	0.24	134392	0.09	0.72	0.91	132545
Hub score	0.22	90756	0.12	0.7	0.88	257855	0.24	132562	0.1	0.69	0.9	130450
Vertex Betweenness	0.21	97254	0.12	0.61	0.88	283358	0.24	129542	0.08	0.69	0.92	129932

Табл. 5. Результаты экспериментов в случае старта от центральных вершин (случайная сеть Эрдёша-Реньи)

	Случайная сеть Эрдёша-Реньи
	EBH Model		SIR Model
	Охват	Время	S	^max	R	Время
Hub	0.99	239344	0.01	0.83	0.99	278457
Hub in	0.99	295347	0.01	0.83	0.99	234906
Hub out	0.99	227332	0.01	0.83	0.99	289885
K-shell	0.99	298324	0.01	0.84	0.99	290434
K-shell in	0.99	289409	0.01	0.83	0.99	230945
K-shell out	0.99	254053	0.01	0.85	0.99	250346
PageRank	0.99	239266	0.01	0.83	0.99	250701
Eigenvector	0.99	238506	0.01	0.85	0.99	285609
Closeness	0.99	240436	0.01	0.8	0.99	234956
Closeness in	0.99	234597	0.01	0.81	0.99	276534
Closeness out	0.99	233419	0.01	0.81	0.99	290584
Authority	0.99	248706	0.01	0.87	0.99	239540
Hub score	0.99	238970	0.01	0.83	0.99	264503
Vertex Betweenness	0.99	238504	0.01	0.83	0.99	281114

Как показывают результаты проведённых экспериментов, даже при запуске процессов распространения от центральных вершин и от вершин из разных оболочек получается почти такой же охват узлов, как и в случае старта от случайной вершины. Отсюда можно сделать вывод, что запуск процессов распространения от вершин с максимальными значениями полученных центральностей и вершин из разных оболочек не индуцирует более масштабный охват, чем в случае запуска от случайных вершин (см. табл. 2–3). Также из таблиц видно, что запуск процессов распространения на эмпирической сети от некоторых центральных вершин (с высокими значениями степени, eigenvector , pagerank , authority , hub score , vertex betweenness ) с использованием EBH – модели будет инициировать процессы, которые охватят вершины за время, которое на порядок ниже, чем в остальных случаях. Можно утверждать, что запуск процессов распространения от этих вершин позволит добиться охвата за более короткое время, что может быть полезно, например, при распространении срочной информации.

Последним этапом проведённого исследования было изучение роли структуры сообществ эмпирической сети и взаимосвязей между ними в процессах распространения информации.

Была построена матрица связей между сообществами, где каждая строка и столбец соответствует сообществу. Значение в I -й строке и j -ом столбце матрицы показывает сколько связей исходит из I -го сообщества в j-ое сообщество. Главная диагональ матрицы, таким образом, содержит количество рёбер внутри сообщества (см. табл. 6).

Табл. 6. Количество связей между сообществами

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	4473	120	14	0	109	187	61	0	6	2	54	0	23	6	6	10	15	0
2	218	12712	111	0	677	3122	1661	3	263	16	1332	46	478	95	306	458	40	4
3	4	61	2541	0	10	28	223	0	1	0	5	0	3	1	2	0	1	0
4	0	0	0	3	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	94	251	34	0	4854	151	113	0	24	5	82	3	43	10	16	85	19	0
6	228	3293	87	0	336	19601	1799	5	342	20	2334	0	866	207	418	976	19	6
7	77	1373	186	0	276	1773	15818	2	35	1	1009	0	154	27	92	272	18	4
8	1	8	0	0	0	4	2	39	1	0	2	0	0	0	1	1	0	0
9	7	71	1	0	38	73	28	0	1616	3	52	0	30	0	6	30	0	0
10	1	13	0	0	5	13	2	0	1	182	3	0	8	0	1	1	1	0
11	104	1150	30	0	296	1914	1442	2	252	2	8238	1	330	79	321	597	22	3
12	1	28	0	0	3	0	0	0	3	0	0	378	0	0	0	0	0	0
13	23	421	2	0	51	488	105	0	22	4	165	0	3719	24	97	55	1	0
14	1	10	2	0	2	31	6	0	4	0	6	0	9	4985	2	0	0	0
15	13	126	2	0	20	146	39	0	15	0	126	0	36	5	1225	32	1	0
16	4	115	0	0	143	141	29	0	12	0	125	0	21	0	15	5640	1	0
17	2	6	2	0	11	3	2	0	0	0	4	0	1	0	0	1	563	0
18	0	6	0	0	1	27	4	0	0	0	10	0	2	0	0	0	0	42

По таблице видно, что сообщество 4, в отличии от других кластеров, никак не связано с другими сообществами, ни входящими рёбрами, ни выходящими. Также можно заметить, что из сообщества 11 существуют выходы во все остальные сообщества и этих выходов достаточно большое количество, кроме, конечно же, 4-го сообщества. Похожим сообществом является кластер 6, но он не связан с сообществом 12.

От разных вершин из сообщества 11 были проведены запуски процессов распространения, полученные результаты были усреднены и отображены на диаграмме, представленной на рис. 16. Диаграмма показывает, что, если инициировать процессы распространения информации от вершин из кластера 11, то моделируемые процессы охватывают все сообщества, кроме 4-го. Это как раз можно объяснить тем, что сообщество 11 плотно связно со всеми остальными кластерами. Стоит также обратить внимание, что в проводимых симуляциях распространения не происходит полный или почти полный охват какого-либо из сообществ.

Аналогично были получены результаты и для сообщества 6. Можно отметить, что кроме сообществ, связанных по исходам с 6-м, информация достигла и сообщества 12, которое напрямую с 6-м не связано.

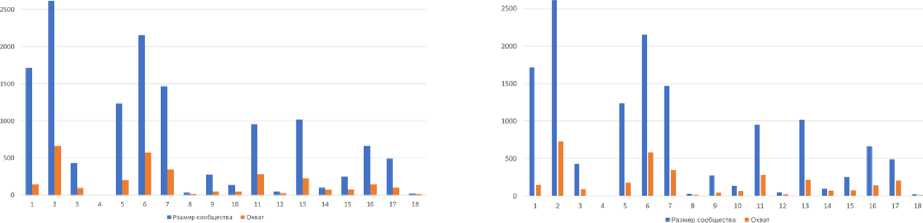
Рис. 16. Соотношение охвата узлов сообщества информацией с его размера (сообщества 11 и 6)

Заключение

Целью работы было изучение влияния структурных и топологических особенностей социальной сети видеохостинга YouTube на процессы распространения информации в YouTube . Для проведения исследования по собранным данным была построена новостная подсеть.

Результаты анализа показали, что исследуемая сеть YouTube – каналов является масштабноинвариантной, относится к слабо-дисассортативным (дисассортативность носит структурный характер) и имеет хорошо выраженные структуры сообществ и ядро-периферия, также анализ формы предпочтительного присоединения позволяет говорить о подлинейном характере предпочтительного присоединения.

Для моделирования процессов распространения информации использовалась иерархическая каскадная модель распространения на основе связей в сети, учитывающая структуры сообществ и ядро-периферия.

Результаты моделирования показали, что инициация распространения от центральных вершин не максимизирует информационный охват сети, но в некоторых случаях существенно сокращает время распространения. Возможно, требуется более детальный анализ или принципиально другой подход для выделения влиятельной вершины-суперраспространителя или набора таких вершин.

Наконец, исследование показало, что при уничтожении структуры сообществ масштаб распространения увеличивается, что позволяет говорить о сообществах как о «ловушке» для распространения информации.

Полученные результаты могут быть основой для решения задач поиска суперраспространителей, блокировки негативного влияния, формирования наборов наиболее влиятельных вершин для решения задач распространения и блокировки.