Изучение совместной фильтрации с помощью метода K-ближайших соседей и факторизации неотрицательной матрицы

DOI:

Modern society's changing environment and the explosion of digital content call for creative approaches to help consumers sort through the sea of choices at their disposal. In this quest, recommender systems have become crucial tools, utilizing user interactions to provide individualized content recommendation [1-3] . Collaborative Filtering (CF), a key technique that relies on the idea that users who have shown similar preferences in the past are likely to share preferences in the future [4-5] is at the core of these systems. With K-Nearest Neighbors (KNN) Regression and Non-Negative Matrix Factorization (NMF), two well-known techniques, this study explores the world of CF. Our research strives to reveal the complexities of Our investigation intends to reveal the subtleties of these methods, assess their effectiveness, and get knowledge on how practically useful they are effective recommender systems are crucial in a time when user engagement depends on the provision of customized experiences. These systems must continuously change to accommodate shifting user expectations and preferences if they are to remain relevant [6]. Our study is in line with the present environment, in which user-centric experiences and data-driven insights are crucial. Our objective is to enable practitioners and researchers to make knowledgeable decisions in the field of recommender systems by examining the mechanics of KNN Regression and NMF. Our work is motivated by 0202

the aim to evaluate the predictive capacity of KNN, and is grounded in recent developments and trends in collaborative filtering. In order to fulfill the changing needs of consumers as technology develops, these strategies must keep up. Our work aims to offer a timely investigation that represents the cutting-edge landscape by grounding our analysis in contemporary discourse and benchmarking against the most recent approaches [7].

We aim to contribute to the ongoing discussion surrounding the choice of recommender systems in a dynamic digital environment through a thorough investigation of KNN Regression and NMF. Our study highlights the adaptability of these strategies within the changing landscape of content consumption by condensing the essence of these techniques and assessing their performance. We conduct an extensive investigation of KNN Regression and NMF on the MovieLens 1M dataset to provide a thorough evaluation. We describe the model training processes, performance measures, and data preprocessing steps used. We measure and analyze the predicted accuracy of these strategies using empirical studies, revealing light on their effectiveness when applied to various user preferences and content categories.

K-Nearest Neighbors Regression

KNN Regression uses similarity as a tool to forecast consumer preferences. The model creates predictions by locating the closest neighbors in a user-item space based on the preferences of similar users. This strategy is based on the common sense idea that people with similar tastes will probably score things similarly [8]. By determining the distances between users, a fixed number of closest neighbors are chosen. The anticipated rating is then calculated as a weighted average of these neighbors' ratings, with closer neighbors having a larger weight. With the help of the MovieLens 1M dataset, we build and assess a KNN Regression model in this work. The user-item matrix of the dataset serves as the basic framework for the model, with rows denoting users, columns denoting items (movies), and cells denoting corresponding ratings [5]. To make performance evaluation easier, the dataset is divided into separate training and testing subsets before the model is trained. We use the mean absolute error (MAE) and the root mean squared error (RMSE) as two commonly used metrics to assess the KNN Regression model's predictive performance. The difference between the expected and actual scores is quantified by the RMSE, with smaller values indicating better performance. MAE, on the other hand, measures the typical size of prediction [9]. These metrics show how well the model can capture user preferences and produce accurate predictions. In order to further our investigation, we convert the predictions based on regression into discrete ratings.

We can now explore crucial classification measures like accuracy, recall, and F1-score thanks to this modification. These metrics provide a more in-depth assessment of the model's effectiveness, notably in terms of its prowess in appropriately categorizing ratings into different groups. This viewpoint offers priceless information into how well the model distinguishes between user preferences. We gain a profound understanding of the mechanics and restrictions of KNN Regression by carefully deconstructing its complexities and recognizing its predicting powers. This thorough investigation offers the groundwork for understanding how KNN Regression functions in the context of recommender systems.

For example, see Figure 1.

Figure 1. K-Nearest Neighbors Regression

KNN Regression uses similar training data points to predict an output for a fresh input. The method measures the separations between the new input and the existing data points, chooses the closest neighbors, and then gives those neighbors weights. A weighted average of the outputs of these neighbors makes up the expected output. When proximity suggests similarity, KNN Regression is helpful for continuous output prediction.

Non-Negative Matrix Factorization (NMF)

Dimensionality reduction, a crucial component of managing big datasets, is a function of NMF's utility. These non-negative matrices are created by breaking down the high-dimensional 0204

user-item interaction matrix into these latent associations between users and objects. These underlying insights are crucial for anticipating missing ratings, which helps to improve the accuracy of recommendations. This dimensionality reduction improves computational effectiveness and makes it easier to spot significant patterns, which eventually raises the caliber of recommendations.

NMF has found use in a variety of corporate environments, including e-commerce and video streaming platforms. Its capacity to find hidden relationships in data offers avenues for content suggestion, targeted advertising, and personalized marketing. Businesses can better serve their customers by customizing their offerings to their tastes by converting user-item interactions into interpretable latent features.

The successful application of NMF in real-world situations serves as an example of its adaptability. For instance, the foundation for comprehending the principles of NMF in the context of learning object components was established by Lee and Seung's fundamental work from 1999 [10]. Further insights into the applicability of the technique were provided by Gillis' thorough investigation of NMF for polybasic data [11]. The relevance of NMF's contributions to collaborative filtering and data analysis is shown by these references. As we continue our investigation, we'll apply NMF to the MovieLens 1M dataset to gauge how well it performs in real-world scenarios. We want to give thorough insights that support practitioners and researchers in unlocking the potential of NMF for enhanced recommendation systems by closely examining its predictive accuracy, scalability, and flexibility. Here is figure.2

Algorithm 2 Non-Negative Matrix Factorization (NMF)

Require: Data matrix: X € R^mX", rank: r, number of iterations: T Ensure: Factorized matrices: IV e R^mXr, H € R^rxn

• 1:    Initialize:

• 2:    Randomly initialize non-negative matrices IV and H with values between 0 and a predefined maximum value.

• 3:    for t = 1 to T do

• 4:    Update H:

• 5:    Compute the numerator: Nh = IV^TX

• 6:    Compute the denominator: Dh — W^rlVH 4- e

• 7:    Update matrix H: H t- H Q ^-, where © represents element-wise multiplication.

• &  Update IV:

• 9:   Compute the numerator: Л^гил = XH^T

• 10:    Compute the denominator: Du- = WHH^T + e

• 11:    Update matrix IV: IV 4— IV ©

• 12:    end for

Figure 2. Non-Negative Matrix Factorization (NMF)

In order to enable feature extraction, NMF splits a given data matrix into two non-negative matrices. The $W$ and $H$ factor matrices are updated iteratively by optimizing their products to closely resemble the original matrix.

METHODOLOGY

Data Collection

The "MovieLens 1M" dataset from the Internet Movie Database (IMDb), a well-known online destination for movies, TV series, and related content, served as the basis for this study. The MovieLens dataset is crucial for research on collaborative filtering and is an important tool for assessing algorithmic recommendations [8, 12]. Due of its essential ability to record usermovie interactions, the MovieLens 1M dataset is particularly important in research on collaborative filtering. Using previous interactions and user similarities, collaborative filtering, a crucial technique in recommendation systems, predicts users' preferences.

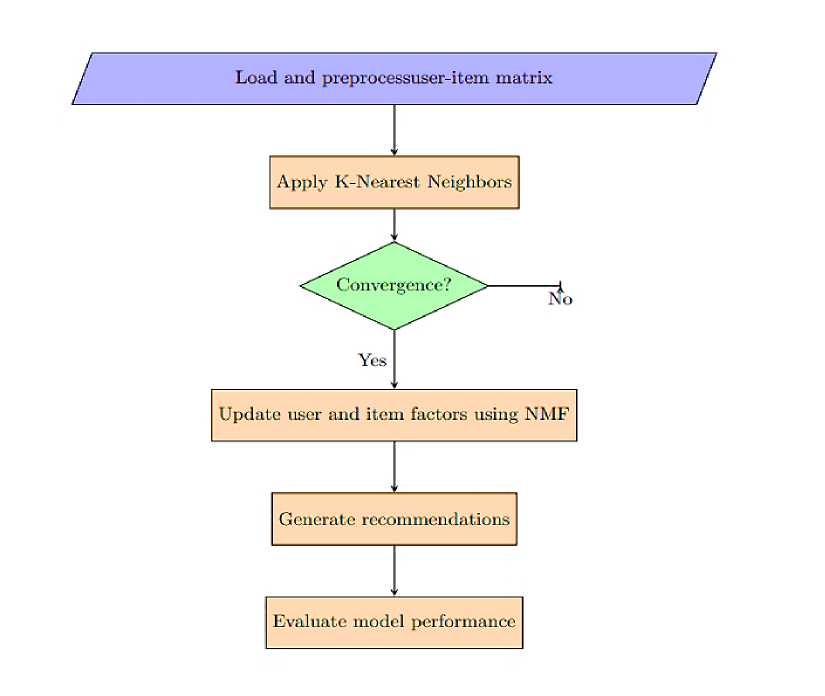
Figure 3. K-Nearest Neighbors and Non-Negative Matrix Factorization framework.

The user IDs, movie IDs, and rating information in the dataset are essential for building collaborative filtering algorithms that take advantage of user behaviors for precise predictions. The timestamps also provide the chance for temporal analysis, making it possible to examine how preferences change over time and improving our understanding of user behaviors in general. After that here is the figure showing the process and way.

In this study, we load and preprocess the user-item matrix, which contains user-item interactions or ratings, to get started. The K-Nearest Neighbors (KNN) algorithm is then used to find equivalent patterns in the data, allowing us to find users or products that are similar to them. In the meantime, latent features from the user-item matrix are extracted using the NonNegative Matrix Factorization (NMF) technique, providing a thorough grasp of the underlying data patterns. By combining user and item factors using these approaches, we produce customized suggestions. We assess the model's performance using well-recognized metrics like precision, recall, and F1-score to determine the effectiveness of our strategy. Additionally, we use cross-validation techniques to guarantee the model's robustness and generalizability. This comprehensive architecture serves as a foundation for developing efficient recommendation systems while also advancing our understanding of collaborative filtering.

RESULT AND DISCUSSION

KNearest Neighbors (KNN) Performance Metrics

Metrics

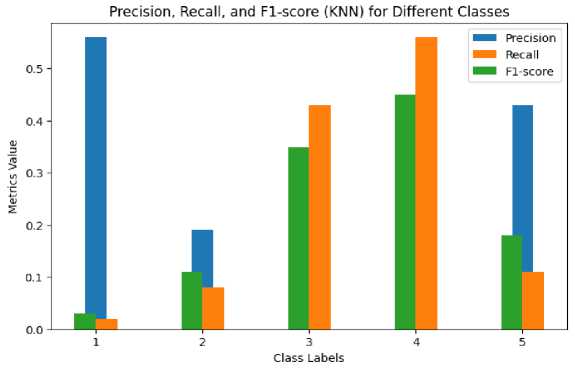
Figure 5. Precision, Recall, and F1 score (KNN).

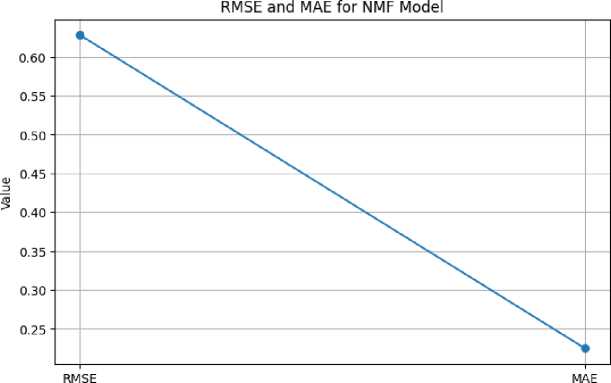
The Non-Negative Matrix Factorization (NMF) model showed promise in our research. Figure 4 and figure 5 shown that the model's low Root Mean Squared Error (RMSE) of roughly 0.63 and its low Mean Absolute Error (MAE) of roughly 0.22 demonstrate its capacity to precisely forecast ratings and give users specific recommendations.

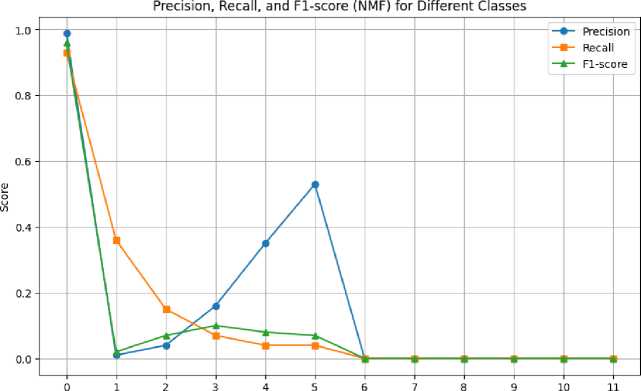
The NMF model showed distinct performance across rating categories in terms of the classification metrics. With a noteworthy recall of 0.93 and a high F1-score of 0.96, it successfully predicted ratings in category 0.0 with a high precision of 0.99. The model's performance, however, differed when used to predict additional rating categories, with poorer precision, recall, and F1-scores. For instance, category 1.0 had a moderate F1-score of 0.02 due to precision of 0.01 and recall of 0.36.

Metrics

Class

Figure 7. Precision, Recall, and F1-score (NMF).

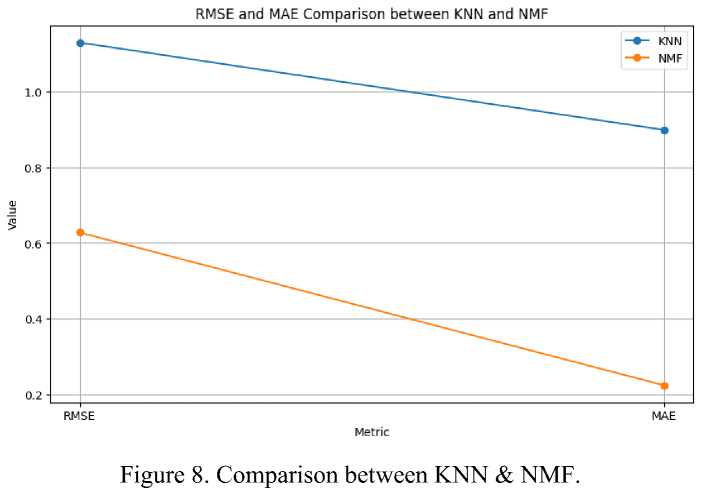
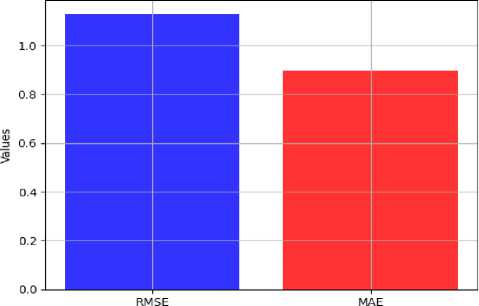
Based on the results of our experiments, we found that NMF performed better than KNN in terms of RMSE and MAE. The RMSE for KNN was determined to be 1.13, while the RMSE for NMF was considerably lower at 0.63. Similarly, KNN's MAE was 0.90, but NMF's MAE was 0.22, indicating a markedly superior performance.

CONCLUSION

Finally, our research explores collaborative filtering with an emphasis on Non-Negative Matrix Factorization (NMF) and K-Nearest Neighbors (KNN) Regression techniques. In a time of common digital content, these methods are crucial for providing users with individualized content recommendations that take into account their changing interests and demonstrates NMF's improved prediction accuracy, as demonstrated by lower RMSE and MAE values compared to KNN Regression, by comparing KNN Regression with NMF on the MovieLens 1M dataset. Additionally, NMF exhibits promise in predicting a variety of rating categories, demonstrating its flexibility and accuracy and provides researchers as well as professionals with useful advice on how to design effective recommendation systems that change with user needs and technical trends. These insights inform the creation of recommendation strategies that improve user experiences as the digital landscape changes.