Изучение влияния шумов детектора на погрешности количественных анализов нуклеиновых кислот на приборах ПЦР-РВ

При разработке анализаторов нуклеиновых кислот основной задачей является уменьшение объема реактивов в пробирках для количественных анализов методом полимеразной цепной реакции в реальном времени (ПЦР-РВ). При меньшем объеме реактивов уменьшается стоимость каждого анализа и повышается быстродействие амплифи-катора за счет уменьшения тепловой инерции. Нижний допустимый предел объема реактивов в пробирках при количественных анализах методом ПЦР-РВ ограничен чувствительностью флуори-метрического детектора. В работе [1] был выполнен практический анализ погрешностей количественных измерений методом ПЦР-РВ при различных способах расчета порогового цикла. Выяснены вклады различных составляющих погрешностей при количественных измерениях. Показано, что из-за разброса свойств реактивов возникают трудности при выделении вкладов в погрешности измерений, вносимых шумами флуориметрическо-го детектора. В настоящей статье выполнено моделирование сигналов ПЦР-РВ при различных уровнях шума. Модельные сигналы использованы для сравнения эффективности способов фильтрации и аппроксимации сигналов при количественных анализах нуклеиновых кислот.

ЭФФЕКТИВНОСТЬ ФИЛЬТРАЦИИ СИГНАЛОВ ПЦР-РВ

В основе метода ПЦР-РВ лежит наблюдение в реальном времени сигналов флуоресценции в ходе реакции. Концентрация исходных специфических фрагментов ДНК увеличивается приблизи- тельно как 2n, где n — текущее количество циклов. Процесс завершения ПЦР обусловлен расходом реагентов при накоплении специфических продуктов амплификации. Поэтому в процессе увеличения количества циклов можно условно выделить 3 участка. На первом участке сигнал флуоресценции специфических фрагментов ДНК находится на уровне, ниже шума. Второй участок можно назвать информационным: на нем наблюдается рост сигнала флуоресценции. На третьем участке увеличения сигнала флуоресценции не происходит.

Исходный модельный сигнал, приведенный на рис. 1, был получен из реальных сигналов ПЦР-РВ анализатора нуклеиновых кислот АНК-32, который серийно выпускается ИАП РАН [2]. Для этого был вычислен усредненный нормированный сигнал ПЦР от 31 пробирки с одинаковыми реактивами; первому участку в течение 14 температурных циклов усредненного сигнала присвоены нулевые значения, а третьему участку от 30 до 50 циклов были присвоены значения 1000 относительных единиц (о.е.).

Если обозначить значение модельного сигнала флуоресценции Y n ( n — номер цикла), то в качестве полезного аналитического сигнала ПЦР можно выбрать приращение интенсивности флуоресценции L 1 или L 5 за 1 или 5 циклов в середине графика, где наблюдается максимальная крутизна.

Максимальное приращение исходного модельного сигнала ПЦР за один цикл (цикл № 24) равно

L 1 = Y 24 – Y 23 = 598 – 416 = 182 о.е.

Приращение за пять циклов (циклы № 22–26) равно

L 5 = Y 26 – Y 21 = 864 – 150 = 714 о.е.

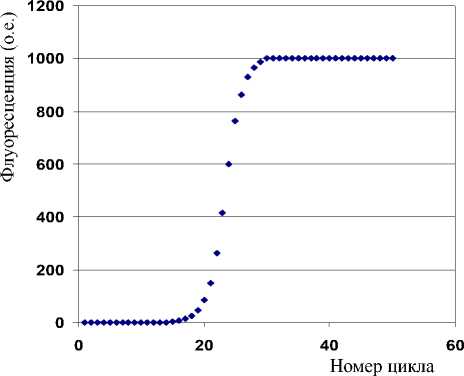
Рис. 1. Исходный модельный сигнал ПЦР-РВ

В большинстве случаев в результате фильтрации приращение сигнала флуоресценции L1f или L5f уменьшается. В качестве исходных модельных шумовых сигналов использовались 10 последовательностей 50 случайных чисел (рис. 2). Интенсивности исходных шумовых сигналов определялись путем вычисления стандартного отклонения S. При максимальной амплитуде однополярного шума, равной одной относительной единице, стандартное отклонение S = 0.31 о.е., а после фильтрации величина Sf ≤ S.

С целью определения улучшения отношения сигнала к шуму K (эффективность фильтрации) предложены следующие предварительные критерии:

• –    относительное уменьшение полезного сигнала ПЦР L o = L f / L ;

• –    относительное изменение интенсивности шума S o = S f / S .

Применение относительных величин позволяет исключить влияние масштабов исходных величин. В результате эффективность фильтрации K (о.е.) можно выразить следующим образом:

K = L / S .

Желательно, чтобы после фильтрации величина L o незначительно отличалась от 1, а величина S o была минимальной.

С целью сравнения эффективности были использованы следующие фильтры [3–6]:

• –    скользящее среднее значение (прямоугольное окно) по 3 циклам (далее — С3);

• –    последовательное применение этого фильтра 2 и 3 раза (2С3 и 3С3);

• –    скользящее среднее значение по 5 циклам (С5);

• –    фильтр Savitzky-Golay (Савицкого—Голея, СГ);

• –    спектральный фильтр (СП);

• –    медиана по 3 и 5 точкам (М3 и М5).

  

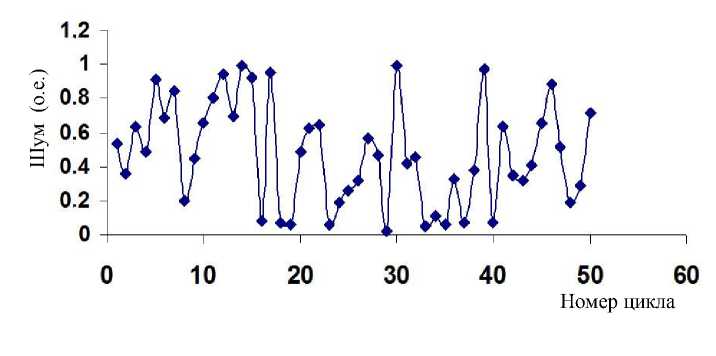
  Рис. 2. Один из исходных модельных шумовых сигналов.

  По горизонтальной оси — номер цикла n , по вертикальной оси — величина шума в относительных единицах. Для наглядности дискретные значения шумового сигнала условно соединены линиями

  
  

Результаты фильтрации сигнала Y n для цикла с номером n могут быть выражены в следующем виде:

• Y С3, n = ( Y n –1 + Y n + Y n +1 )/3;

• Y 2С3, n = ( Y n– 2 + 2 Y n– 1 + 3 Y n + 2 Y n +1 + Y n +2 )/9;

• Y 3С3, n = ( Y n– 3 + 3 Y n– 2 + 6 Y n– 1 + 7 Y n + 6 Y n +1 + +3 Y n +2 + Y n +3 )/27;

• Y С5, n = ( Y n– 2 + Y n– 1 + Y n + Y n +1 + Y n +2 )/5;

• Y СГ, n = (–2 Y n– 3 + 3 Y n– 2 + 6 Y n– 1 + 7 Y n + 6 Y n +1 + + 3 Y n +2 –2 Y n +3 )/21.

Фильтр СГ называют также фильтром полиномиального цифрового сглаживания на основе метода наименьших квадратов (реализован в программе Matlab).

Спектральный фильтр был реализован следующим способом. После фурье-преобразования действительная и мнимая части спектра умножались на спадающую экспоненциальную функцию EXP(–0.1·(f – 1)), где f — порядковый номер спек- тральной точки; например, при f = 2 значение EXP(–0.1) = 0.9048 соответствует ослаблению величины сигнала второй точки по сравнению с величиной сигнала первой точки спектра. В качестве фильтрованного сигнала ПЦР использовалась реальная часть обратного фурье-преобразования.

Медиана выделяет число, которое является серединой упорядоченного множества значений нечетного числа членов.

Результаты применения фильтрации к модельным сигналам ПЦР и шума приведены в табл. 1.

Видно, что медиана совершенно не изменяет приращение интенсивности флуоресценции ( L o = = 1). Это свойство медианы означает, что шумы фильтруются только на части сигнала вне этого участка. Лучшие результаты (значения K больше 2) получены при использовании 3-кратной фильтрации прямоугольным окном по 3 точкам. Можно предположить, что величина K 1 будет иметь существенное значение при последующей аппроксимации графика по 2 точкам, а K 5 — при аппроксимации графика по многим точкам.

Табл. 1. Сравнение эффективности фильтров K (о.е.)

Фильтр	L o1	L o5	S o	K 1	K 5
С3	0.92	0.96	0.52	1.77	1.85
2С3	0.85	0.92	0.43	1.98	2.14
3С3	0.80	0.89	0.38	2.11	2.34
С5	0.79	0.88	0.40	1.98	2.20
СГ	0.93	0.99	0.57	1.63	1.74
СП	0.8	0.86	0.44	1.82	1.95
М3	1	1	0.71	1.41	1.41
М5	1	1	0.62	1.61	1.61

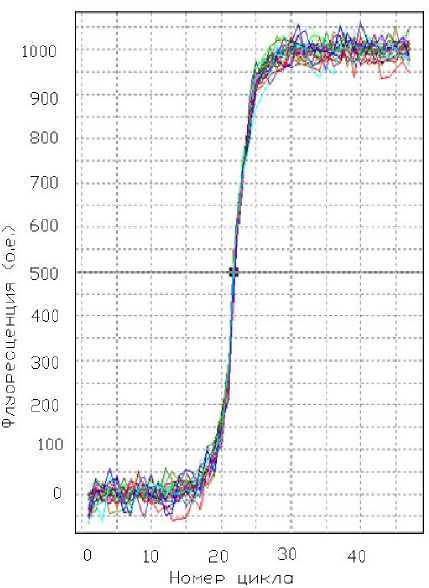
Рис. 3. Графики модельных сигналов ПЦР с разными уровнями шума

ПОГРЕШНОСТИ РАСЧЕТА ПОРОГОВОГО ЦИКЛА БЕЗ ФИЛЬТРАЦИИ

Для оценки влияния шума на погрешности измерения пороговых циклов исходный модельный сигнал, содержащий одно числовое значение при каждом температурном цикле, суммировался со случайными числами. При амплитуде исходного модельного сигнала 1000 относительных единиц (о.е.) выбирались следующие максимальные величины однополярных случайных чисел: 25, 50 и 100 о.е. В результате получались 3 блока суммарных модельных сигналов с разными величинами случайных чисел. Каждый из 10 сигналов в одном блоке отличается от другого последовательностями случайных чисел. Три блока суммарных модельных сигналов и исходный модельный сигнал вводились в программу анализатора АНК-32 в качестве имитации сигналов от пробирок.

В программе анализатора была выполнена нормировка: привязка к нулю среднего значения сигналов от 1 до 14 циклов и привязка к 1000 среднего значения сигналов от 30 до 50 циклов. При нормировке на начальном участке шумовые сигналы становятся симметричными относительно нуля. При этом максимальные амплитуды шума для трех наборов сигналов соответствуют 12.5, 25 и 50 о.е. На рис. 3 приведены одновременно графики всех суммарных модельных сигналов и линия на уровне 500 о.е.

Анализаторы АНК позволяют рассчитать пороговые циклы методом порога, используя разные способы аппроксимации: способ кусочнолинейной аппроксимации по двум точкам (в дальнейшем — АДТ), способ аппроксимации по всем точкам графика (АВТ), а также способ аппроксимации на базе S-образной функции (АСФ) [7]. Для сравнения этих методов выполнена оценка погрешности измерения путем расчета значений стандартного отклонения S пороговых циклов 3 блоков, содержащих по 10 суммарных модельных сигналов.

Результаты расчета погрешностей пороговых циклов приведены в табл. 2. Погрешности пороговых циклов в табл. 2 и следующей таблице вычислены как отношение к одному циклу; например, S = 0.029 соответствует погрешности 2.9 % от одного цикла.

Видно, что величины стандартного отклонения при различных способах расчета пороговых циклов имеют близкие значения и приблизительно линейно зависят от уровня шума.

Табл. 2 . Значения стандартного отклонения S при различных способах расчета пороговых циклов в зависимости от уровня шума при пороге 500 о.е.

Амплитуда шума (о.е.)	Способы расчета пороговых циклов
	S при АДТ	S при АВТ	S при АСФ
12.5	0.029	0.022	0.021
25	0.056	0.047	0.047
50	0.117	0.095	0.099

Табл. 3. Величины стандартного отклонения S и отклонения среднего значения D при различных способах фильтрации и способах расчета пороговых циклов

Фильтры	Критерии	АДТ	АВТ	АСФ
Нет	S	0.123	0.094	0.080
	D	0.036	0.017	0.019
3С3	S	0.092	0.083	0.079
	D	0.002	–0.014	0.012
СГ	S	0.102	0.093	0.084
	D	0.001	0.015	0.008

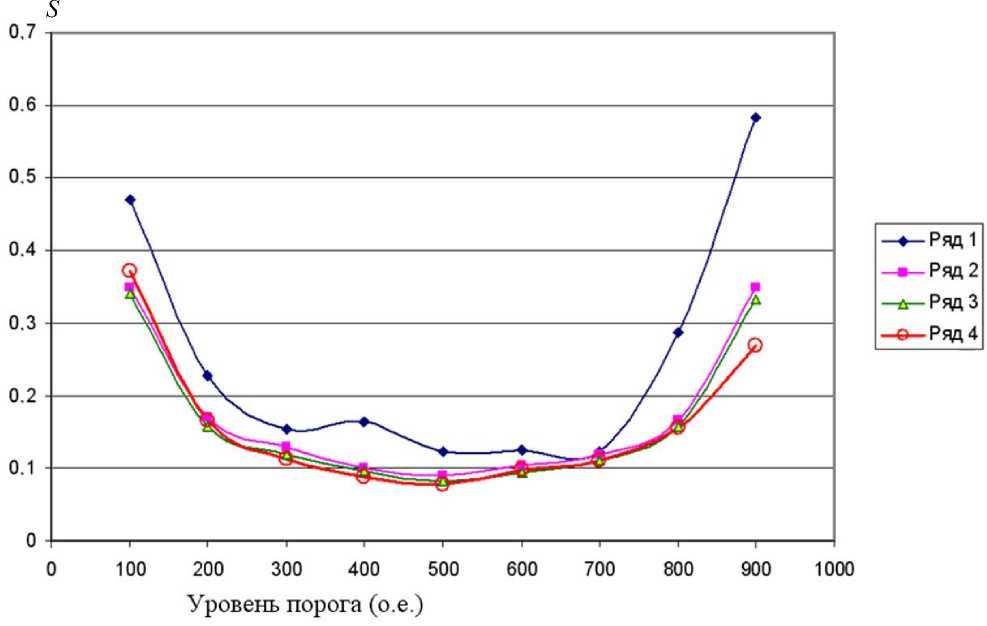
Рис. 4. Зависимости значений стандартного отклонения S от уровня порога.

Ряд 1 — АДТ без фильтра; ряд 2 — АДТ с фильтром 3С3; ряд 3 — АВТ с фильтром 3С3; ряд 4 — АСФ с фильтром 3С3

ВЛИЯНИЕ ФИЛЬТРАЦИИ НА ПОГРЕШНОСТИ РАСЧЕТА ПОРОГОВЫХ ЦИКЛОВ

Для достижения минимальной погрешности пороговых циклов необходимо оптимизировать выбор трех уровней на графиках сигналов ПЦР: уровни привязки к нулю и к максимальному значению, а также уровень порога.

Для определения уровней привязки к нулю и к максимальному значению можно рекомендовать участки, на которых даже после фильтрации не заметно изменение сигнала флуоресценции. Необходимо также исключать несколько точек в начале и конце графика, которые не могут быть правильно отфильтрованы (некоторые фильтры усредняют значения по 7 температурным циклам). Уровни привязки вычисляются как средняя величина сигналов на выбранном участке, т. е. добавляется еще одно звено фильтрации шумов. Рекомендации для выбора оптимального уровня порога (500 о.е.) приведены ниже.

С целью сравнения эффективности фильтров при разных методах расчета были использованы 10 модельных сигналов при уровне шума 50 о.е.

При расчете значений S пороговых циклов для привязки к нулю выбран участок от 5 до 10 циклов, для привязки к 1000 — участок от 35 до 40 циклов. Уровень порога выбран 500 о.е. Результаты расчета приведены в табл. 3. Видно, что наибольшая величина S наблюдается при способе АДТ без фильтрации, а наименьшая величина — при АСФ с фильтром 3С3 . Фильтр 3С3 уменьшает величину S при АДТ на 25 %, а при АСФ — только на 1 %.

В этой таблице приведен еще один критерий для сравнения влияния фильтров — отклонение среднего значения D вычисленных пороговых циклов с использованием фильтров от порогового цикла исходного сигнала. Можно отметить, что величина D значительно меньше S и поэтому не вносит заметного вклада в погрешности измерения.

В табл. 3 приведены значения S при пороге 500 о.е., однако при изменении уровня порога величины стандартного отклонения изменяются (рис. 4).

На графике ряд 1 (АДТ без фильтра) величины S сильно зависят от уровня порога. При использовании фильтрации сигналов ПЦР зависимости ве- личин S от уровня порога для разных способов аппроксимации практически совпадают, при этом минимальные величины S наблюдаются при пороге 500 о.е. Этот уровень порога можно считать оптимальным.

ВЫВОДЫ

С помощью предложенных модельных сигналов установлено, что при увеличении уровня шума происходит приблизительно линейное увеличение стандартного отклонения пороговых циклов.

На основе предложенных критериев выполнено сравнение эффективности нескольких типов фильтров сигналов ПЦР-РВ. Лучшие результаты получены при использовании 3-кратной фильтрации с помощью скользящего среднего значения по 3 пороговым циклам.

Исследовано влияние фильтрации на погрешности расчета пороговых циклов. Даны рекомендации по выбору участков для нормировки сигналов. Показано, что разные способы аппроксимации могут быть дополнены предварительной фильтрацией сигналов ПЦР, при этом способ аппроксимации по двум точкам по величине стандартного отклонения приближается к двум другим более сложным способам аппроксимации.

Исследована зависимость погрешности расчета пороговых циклов от уровня порога. В результате при расчетах может быть рекомендован уровень порога 500 о.е., при котором получаются минимальные погрешности измерения.

Полученные результаты позволяют пользователю выбрать объем реактивов в пробирках при количественных анализах ПЦР на основе критериев: допустимого уровня шума и допустимой погрешности измерения. Например, в соответствии с табл. 1 при максимальной амплитуде шума 12.5 о.е. и сигнале 1000 о.е. стандартное отклонение S имеет приблизительно величину 0.02 или 2 % порогового цикла. Примерно такие результаты получаются при реальных анализах ПЦР с объемом реактивов 23 мкл и объемом пробы 2 мкл.