Извлечение алифатических аминокислот из водных сред аминофосфоновым ионообменником

Ионообменный метод позволяет выделять биологически активные соединения, в частности аминокислоты, из водных растворов. Большинство ионообменников, сорбирующих органические соединения, и собственно аминокислоты относятся к классу слабых электролитов, поэтому межфазное распределение в таких системах в значительной степени зависит от значения рН среды [1–4]. Выделения целевых компонентов осуществляется в динамическом режиме, который позволяет обеспечивать селективное распределение компонентов между ионообменником, полное использование сорбционной емкости и значительное сокращение временных затрат [5–8].

Известно, что ионный обмен представляет собой многостадийный гетерогенный процесс, который включает транспорт ионов сорб-тива в жидкой фазе к поверхности зерна и удаление от нее десорбируемых ионов, межфазный перенос, диффузию сорбируемых и десорбируемых ионов внутри зерна, поскольку не все функциональные группы сорбента локализованы на поверхности, и обратимую реакцию ионного обмена. Широко распространены процессы, интенсивность которых определяется переносом компонентов в пограничном слое раствора и в зерне ионообменника, либо одним из них, при этом скорость ионного обмена определяется коэффициентами внешней и внутренней диффузии.

Надежное математическое описание сорбционного процесса позволяет прогнозировать поведение системы ионообменник-раствор при разных сочетаниях основных параметров, влияющих на эффективность поглощения, – скорости потока, концентрации сорбтива, высоты слоя ионообменника, среднего размера зерна ионообменника и т. д. – без проведения дополнительного эксперимента. Для оценки влияния на процесс сорбции аминокислот гидродинамических условий его проведения использовано асимптотическое уравнение динамики сорбции [9]. В работе [10] предложено математическое описание динамики ионообменной сорбции, основанное на использовании внешнедиффузионной модели без учета продольной диффузии. Проведенный авторами данной работы анализ моделей динамики сорбции и сравнение результатов расчета с экспериментальным материалом позволили выбрать модель Томаса [11], несколько модернизировав её.

Цель работы – изучение сорбции алифатических аминокислот – глицина и α-аланина аминофосфоновым ионообменником марки Purolite S950 и описание динамики сорбции с помощью кинетического уравнения зависимости степени извлечения компонента от продолжительности контакта раствора со слоем сорбента, учитывающего влияние на процесс диффузионных сопротивлений в каналах слоя и зернах ионообменника в колонне с неподвижной загрузкой.

Материалы и методы

В настоящей работе сконструирована экспериментальная установка, позволяющая проводить исследования по очистке воды от различных примесей и выделению из раствора целевых компонентов. Многоплановость установки достигнута тем, что очищаемый раствор и регенерирующий или элюирующий реагент пропускаются через слой ионообменной смолы в различном направлении.

Установка, представленная на рисунке 1, состоит из емкости 1 с очищаемым раствором, которая с помощью гибких шлангов присоединена к перистальтическому насосу 2 марки РР2–15 позволяющему прокачивать и регулировать скорость подачи жидкости в интервале от 1 до 200 см3/мин, контроль подачи жидкости осуществляется ротаметром 3.

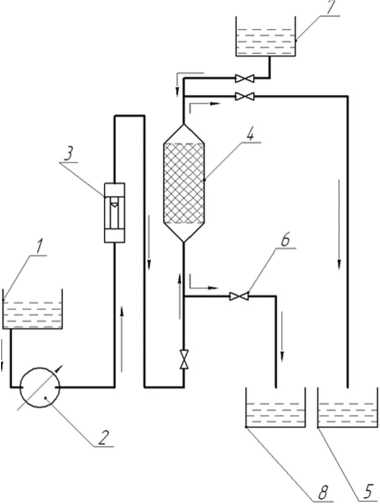
Рисунок 1. Схема экспериментальной ионообменной установки

• Figure 1. Experimental ion exchange plant scheme

По жестким трубкам диаметром 12 мм раствор подается снизу в вертикальный закрытый цилиндрический резервуар 4 с внутренним диаметром 56 мм и высотой 158 мм, заполненный ионообменной смолой. В верхней части колонны проводится отбор очищенной жидкости в специальную емкость 5. Вход и выход колоны снабжены вентилями 6, позволяющими перекрывать поток жидкости и направлять ее поток снизу вверх или сверху вниз. Регенерирующий раствор находится в ёмкости 7 и подаётся сверху вниз. Сбор регенерирующей жидкости осуществляется в ёмкость 8.

Цикл работы установки включает четыре стадии:

• 1.    сорбция удаляемого или целевого компонента из раствора, при которой очищаемая жидкость проходит сквозь слой ионообменного сорбента снизу вверх;

• 2.    расширение и перемешивание слоя ионообменной смолы, причем данная стадия протекает одновременно с первой за счет перемещения ионообменного слоя при подаче жидкости снизу, что является несомненным достоинством данной установки;

• 3.    регенерация ионообменной смолы, при которой соответствующим образом приготовленный регенерирующий раствор проходит через загрузку сверху вниз и восстанавливает исходные свойства сорбента или десорбирует целевой компонент;

• 4.    промывка сорбента, то есть удаление регенерирующего раствора в результате промывки водой сверху вниз.

В установке применена неподвижная загрузка сорбента. Рабочий цикл ионообменника зависит от обменной емкости, определяющейся типом сорбента и, следовательно, устанавливающий объем жидкости, обрабатываемой между двумя операциями регенерации. Трудности, связанные с системой сбора очищенного раствора выше верхнего слоя ионообменного материала решены использованием перистальтического насоса.

Регенерирующий или элюирующий раствор используется достаточно эффективно, поскольку он последовательно проходит через слои ионообменного материала с возрастающей степенью насыщенности, что достигается направлением потока противоположным движению обрабатываемой жидкости.

Динамику сорбции аминокислот изучали на модельных растворах с концентрациями от 0,01 до 0,05 моль/дм3 при температуре 298 ± 3 К. Водородный показатель исходного раствора составлял рН 5,0, поскольку, согласно диаграммам распределения ионных форм, аминокислоты находятся при этой кислотности в виде биполярных ионов. Противоточную ионообменную установку с неподвижной загрузкой сорбента заполняли полиамфолитом в Н± форме, очищаемый раствор пропускали со скоростями от 3 до 9 см3/мин. В ходе эксперимента осуществлялся отбор проб раствора на выходе через каждые 10 мин. Концентрацию аминокислот определяли методом Попа и Стивенса [12]. Процесс продолжали до выравнивания концентрации аминокислоты на входе в колонну и выходе из неё. Количество поглощенного ионообменником вещества определяли по разности концентраций исходного раствора и раствора на выходе в данный момент времени и рассчитывали отношение концентрации в данный момент времени (с) к начальной концентрации (с0). По полученным данным строили выходные кривые в координатах с/с0 от времени τ.

Результаты

В работе получены экспериментальные выходные кривые сорбции биполярных ионов глицина и α-аланина на аминофосфоновом ионообменнике Purolite S950 в протонированной форме (рисунки 2 и 3). Сорбционный фронт имеет форму «волны». В начальный момент наблюдается обострение фронта сорбции, соответствующее внешнедиффузионной кинетике, обусловленное низкими значениями коэффициента внутренней диффузии. Размытие фронта сорбции при увеличении заполнения ионообменника связано с увеличением вклада внутренней диффузии.

В работе предложено описание динамики ионного обмена, учитывающее полное диффузионное сопротивление и нелинейный характер зависимости равновесных концентраций компонентов в растворе и фазе сорбента. Полученное кинетическое уравнение применено к описанию динамики сорбции глицинии и α-аланина на аминофосфоновом ионообменнике Purolite S950.

Сорбция рассматривается как массообменный процесс, осложненный гетерогенной химической реакцией, скорость которого описывается дифференциальным уравнением:

∂q = χaF (c, q), ∂Θ где q(x, Θ) – среднеобъемная концентрация вещества в твердой фазе; Θ – продолжительность контакта слоя ионообменника с раствором, Θ = t-x /υ; t – время от начала поступления раствора в колонну; x – расстояние от входа в колонну; υ – средняя скорость течения раствора в каналах слоя; х - кинетический коэффициент, учитывающий диффузионный перенос во взаимодействующих фазах; a – удельная поверхность ионита; F(c, q) – функция движущей силы процесса; с (x, 0) - концентрация вещества в жидкости.

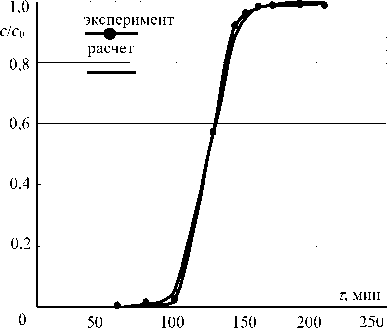
Рисунок 2. Экспериментальная и расчетная выходные кривые сорбции глицина на Purolite S950 (H+) при 298 К, исходной концентрации 0,033 моль/дм ³ и скорости пропускания 5 см ³ /мин

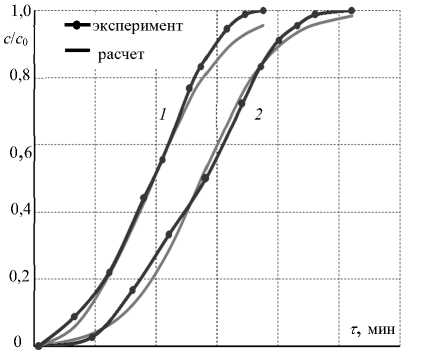
30 60 90      120 150 180 200

Рисунок 3. Экспериментальные и расчетные выходные кривые α-аланина на Purolite S950 (H+) при 298 К и исходной концентрации 0,018 моль/дм ³ ; скорость пропускания 1 – 9 см ³ /мин; 2 – 7 см ³ /мин

Figure 2. Experimental and derived elution sorption curves of glycine using Purolite S950 (H+) at 298 К, initial concentration 0,033 mole/dm ³ and flow rate of 5 сm ³ /min

Figure 3. Experimental and derived elution sorption curves of α-alanine using Purolite S950 (H+) at 298 К and initial concentration 0,018 mole/dm ³ ; Flow rate 1 – 9 сm3/min; 2 – 7 сm3/min

Для описания движущей силы процесса используется выражение

(     q 1 1            q

F(с, q) = cl--|--( со - с У^— , (1) qk  q qmax               qmax где qmах – обменная емкость ионообменника; с0 – начальная концентрация вещества в р-ре; k – коэффициент ионообменного равновесия.

Решение уравнения (1), полученное Томасом [11] в допущении формирования стационарного концентрационного фронта, имеет вид:

c c0

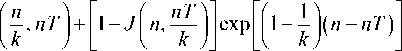
где n - безразмерная высота слоя, n = % ax)U E ;

е - порозность слоя; T - безразмерное время контакта ионообменника с раствором, T = ^{UE C} о ®! xq max ; значения функции

J(а, в = 1 - e - ^в J e - ^z 1 ₀ ( 2 Ув 1 dZ для разных a 0           ^            ^

и в и ее математические свойства табулированы; I 0 – модифицированная функция Бесселя нулевого порядка.

Необходимым условием применения этой математической модели является достаточно надежная оценка кинетического коэффициента х , связанного с коэффициентом переноса сорбируемого компонента в каналах слоя (массоотдача в растворе) и в зернах сорбента (массоотдача в твердой фазе).

Сложность гидродинамической обстановки в каналах слоя ионообменника ограничивает возможность теоретического анализа конвективного переноса. Перенос компонента к поверхности зерен ионита рассматривается аналогичным переносу в трубчатых каналах (капиллярная модель). Авторы полагают допустимость такого подхода к системам, в которых коэффициент молекулярной диффузии компонента в растворе D ж значительно меньше коэффициента кинематической вязкости жидкости v (соответственно число Шмидта Sc = v /D ж >> 1). При больших числах Sc толщина диффузионного пограничного слоя, перенос в котором лимитирует процесс, значительно меньше толщины гидродинамического пограничного слоя, вследствие чего сложная геометрическая конфигурация не должна существенно влиять на массоотдачу.

Капиллярная модель подверглась многосторонней экспериментальной проверке. Опытные результаты, полученные измерением предельных диффузионных токов с окислительновосстановительной реакции на никелевых гранулах и измерением массоотдачи от поверхности прессованных частиц из плохорастворимого вещества в широком интервале чисел Шмидта и Рейнольдса, показали удовлетворительную сходимость с вычисленными.

Для определения коэффициента массоот-дачи жидкости в трубе диаметром d и длиной l при ламинарном режиме течения использовали решение тепловой задачи, полученное Гретцем и Нуссельтом в виде зависимости числа Шервуда (или дифференциального числа Нуссельта) от безразмерной продольной координаты

2 l / d X, =--------.

⁺ ReSc

Результаты расчета на основе капиллярной модели показали удовлетворительной согласие с экспериментальным материалом. При этом в случае зернистого слоя число Рейнольдса Re′ и безразмерная продольная координата x + вычисляются по формулам:

2 x / d x₊ =------ , ⁺ Re * Sc

0,423 £^1,25

d г = —;------ d з ,

• 1    - £

Re' = 0,45 u 0 d з/((1 - £) £ °’5v), где u0 – скорость, отнесенная к полному сечению колонны; x – высота слоя; dг – гидравлический диаметр самого узкого живого сечения каналов; dз – диаметр зерен ионообменника.

При ламинарном режиме течения коэффициент массоотдачи в жидкой фазе вычисляют по формуле

Sh = ^d

D ж

”

= - in 8 _Z( G n / A n ) exp ( - x + A n ) , 2 x     L n =o^{v          7 v 7}J

-+

где G_n и A n - постоянные и собственные значения ряда.

Показано, что в слое из хорошо обтекаемых зерен при Re′ < 26 течение в каналах носит ламинарный характер, при Re′ > 100 – турбулентный, в интервале 26 < Re′ < 100 – переходный режим.

В [13] для вычисления чисел Шервуда при турбулентном течении рекомендуется использовать формулу:

Sh = 0,115 Re(Z /8) 0,5 Sc⁰ , ²⁵ [cth(1,17^ 0 ' ⁵ )]^2/3, где Z — коэффициент гидравлического сопротивления зернистого слоя, определяемый соотношением Z = 30/Re + 3,0/Rе^0,7 + 0,3;

z l = 2,1 - 10 ^{- 3} Sc^0,25 Re'(Z/8)^0,5 x / d _г.

Сравнены расчетные и экспериментальные выходные кривые сорбции биполярного иона глицина и α-аланина на аминофосфоновом ионообменнике Purolite S950, представленные на рисунках 2 и 3. На начальных участках выходных кривых сорбции отклонение достигает 3%; на конечных участках – не превышает 8%, что позволяет использовать предложенную модели для описания динамики сорбции аминокислот в неподвижном слое ионообменника.

Заключение

В работе изучена сорбция алифатических аминокислот – глицина и α-аланина аминофосфоновым ионообменником Purolite S950. На сорбционной установке получены эксери-ментальные выходные кривые сорбции биполярных ионо аминокислот и описаны с помощью кинетического уравнения модернизированной модели Томаса. Модель одномерного капиллярного течения для оценки диффузионного сопротивления при движении жидкости в каналах слоя ионообменника может быть успешно использована для решения сорбционной кинетической задачи по уравнению Томаса. Модернизированная модель динамики сорбции, учитывающая влияние на процесс диффузионных сопротивлений в каналах слоя и зернах ионообменника в колонне с неподвижной загрузкой, адекватно описывает зависимость степени извлечения компонента от продолжительности контакта раствора со слоем ионообменника и может быть использована для расчета выходных кривых сорбции на различных видах ионообменников.

Работа выполнена в соответствие с Координационным планом секции «Адсорбционные явления» научного совета РАН по физической химии, номер темы 22–03–460–21.

Авторы выражают глубокую благодарность д.т.н, профессору ВГУИТ Корниенко Тамаре Сергеевне за ценные замечания и консультации в ходе работы.