Java библиотека для работы с эллиптическими кривыми

DOI:

В настоящее время эллиптические кривые (далее – ЭК) широко используются в криптографии: существует алгоритм Ленстры для факторизации, а также алгоритм проверки числа на простоту на основе ЭК; были разработаны стандарты электронной цифровой подписи (далее – ЭЦП) и шифрования, протокол Диффи-Хеллмана. Данная область криптографии активно развивается и является перспективной [1-4], поэтому для проведения исследований и для разработки новых продуктов и алгоритмов в этой сфере очень удобным становится использование библиотеки, которая бы содержала базовые арифметические операции с точками на эллиптических кривых. Обзор существующих криптографических пакетов для различных языков программирования показал, что зачастую в них отсутствует возможность использования базовых функций (например сложение, скалярное умножение точек и др.), а также поддерживается ограниченное число определенных кривых. Для языка Java существует библиотека ECCelerate, однако в ней нет возможности выбора определенного алгоритма скалярного умножения и выбора, в каких координатах будут представлены точки кривой, нет операции утроения точки и операции пятикратного увеличения по упрощенным формулам, а также нет возможности добавления данного пакета к проекту через фреймворк Apache Maven. Исходя из вышеперечисленных факторов была реализована новая криптографическая Java библиотека для работы с эллиптическими кривыми.

МАТЕРИАЛЫ И МЕТОДЫ

Из общего уравнения Вейерштрасса (1) выводятся уравнения для форм кривых, каждая из которых обладает специфическим набором свойств и формулами для основных операций.

y ² + ay + b = x ³ + cx ² + dx + e

В данной библиотеке были реализованы: каноническая кривая Вейерштрасса, кривая Эдвардса (а также ее скрученный вариант) [5], квартика Якоби [6]. Две последние кривые вызывают большой интерес, поскольку нахождение суммы двух точек, а также удвоение точки на них можно реализовать с меньшими затратами по времени по сравнению с другими формами кривых.

Основными операциями считаются: сложение/вычитание двух различных точек, удвоение и утроение точки (в некоторых случаях можно вывести формулы для пятикратного увеличения), а также скалярное умножение точки, которое реализуется через описанные выше операции. Существует база данных для ЭК [7], созданная математиками Д. Бернштейном и Т. Ланге, которая содержит выведенные формулы для вычисления операций над точками для разных форм кривых. Данная база активно использовалась при реализации данной библиотеки.

Для применения ЭК в криптографии необходимо брать кривые над некоторыми конечными полями. Соответственно приходится иметь дело с модулярной арифметикой и большими числами. В Java есть дополнительный тип данных – BigInteger, разработанный специально для таких вычислений. Многие модулярные функции с этим типом данных имеют оптимизации.

Помимо базовых операций в данной библиотеке были реализованы стандарты ЭЦП: ECDSA [8] и ГОСТ 34.10-2018. Для их создания были использованы криптографические примитивы такие как: символ Лежандра, вероятностный тест простоты Миллера-Рабина, а также алгоритм Тонелли-Шенкса.

Для проведения тестирования использовался фреймворк JUnit. Сборка и развертывание проводилось при помощи фреймворка Apache Maven.

РЕЗУЛЬТАТЫ

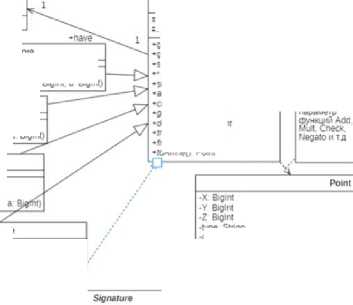
Было выделено два абстрактных класса: Elliptic_curve (ЭК) и Signature (ЭЦП). Каждый абстрактный класс имеет классы, которые его реализуют: для ЭК это определенные формы кривых, а для ЭЦП это классы стандартов ECDSA и ГОСТ 34.102018. На рисунке 1 представлена UML-диаграмма классов проекта.

Finite_held

геттеры сеттеры

-Cnaractenstrc Bigint

■Degree int

-Order Bigint

■PrimiDve_eiem

■toJacoDii) Point

-tornvenedO Point

*EaIi.’a,as_curveileKi Fnitejeld c Bigint d Bigint)

■toXXYZZi) Po-nt

►IOXXYZZR0 Point

►toExtendedO

►Twistoo_Edwafd»jCurve(heid; Rrwejw. a Bigint о Вдигк)

EHiptic_cuiw

Coefficients ArrayLst «Bigint» xFi&d Finite Dm

Pomt входной параметр

•PointCcurve Elliptic .curve}

■P»nt(curve Eiiiptic'curve к Bigint у Bigint)

‘Pc*nt(curve Eibptic^curve coords ArrayList«B«gint» type String)

•coords ArraytBt

•randomPomtCurveO Pont substracto Point todPomrsO Point rhecKPpintO boolean jerNegatoO Point OouBiePomtO Point tnpiePointO Point ’ivePotntO Point :оАгт.пео Point

-ae^areKeyso Arrayu$t

*generareS>gnaiureO Array! ist«OCyecp

•cnecKSionarureO oocwan

-G Pomt “

-n Bigint

• • md MessageDigest

  -secureRandom SecureRandom

• ■ n Bigint

  -muit.alg

  -add.mode

■oase ust

GOST.34.10.2018

■curve Snort_We:er5trass_curve

• - q Bigint

• - P Point

• -md MessageDigest

  -secureRanOom secureRandom

-addjnode Sin ng

-base List «Bigint»

Рисунок 1. UML-диаграмма классов проекта.

• Figure 1 . UML class diagram of the project.

Функция скалярного умножения - scalarMultPoint() представлена в двух формах. Первая реализует метод умножения mbNAF [9], а вторая методы: удвоения-сложения (double-and-add), NAF метод (binary_NAF), NAF метод с некоторым окном предвычислений (NAF_w), а также метод лестницы Монтгомери (montgomery_ladder). Обе реализации принимают на вход параметр add_mode, который устанавливает в каком координатном представлении будет происходить умножение. Перевод в аффинные координаты в конце не производится – это действие остается на усмотрении пользователя. Вторая реализация принимает на вход параметр alg_name, указывающий алгоритм скалярного умножения.

В классах ECDSA и GOST_34_10_2018 при формировании основных параметров было необходимо находить произвольную точку на кривой. Специально для этого была написана функция randomPointCurve(), реализация которой использовала алгоритм Тонелли-Шенкса. Также были добавлены конструкторы, в которых параметр curve (эллиптическая кривая) может быть выбран из списка рекомендованных кривых, включая рекомендации NIST [10] и рекомендации Росстандарта [11].

В ходе работы было проведено сравнение методов ECDSA для создания электронной подписи, реализованных в данном проекте, с существующими решениями в этой области, включая класс Signature из пакета java.security. Были рассмотрены кривые P-256, P-384 и P-512. На рисунке 2 представлен график, полученный в результате проведенного исследования.

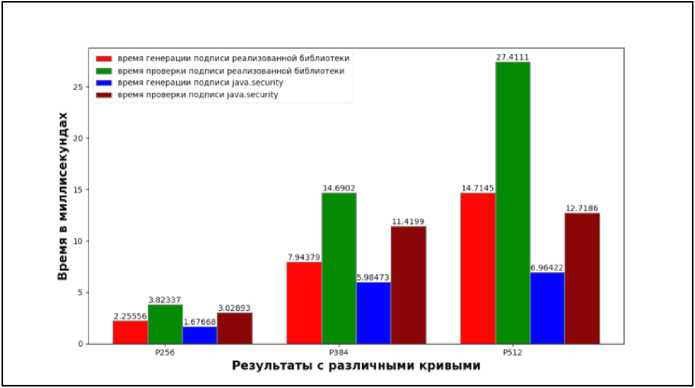
Рисунок 2. Сравнение быстродействия реализаций ECDSA.

Figure 2. Performance comparison of ECDSA implementations.

С целью обеспечения доступности данной библиотеки для любого Java-разработчика, было принято решение опубликовать артефакт в центральном репозитории Maven Central. На рисунке 3 представлена информация о проекте, доступная на сайте MVN Repository после его размещения.

License

» 1.0.0

Java library designed to work with elliptic curves

1Ш2ЕШ

Homepage

Jun 03, 2023

Files

pom (7 KB) jar (89 KB) View All

Repositories

Ranking

#353594 in MvnRepository (See Top Artifacts)

Vulnerabilities from dependencies:

CVE-2019 12415

Vulnerabilities

CVE-2017-5644

CVE-2017 12626

View 1 more ...

Maven |[ Cradle | [ Cradle (Sh ort) Ifcrad le (Kotlin) ][ SBT || l vy[[ Grape ][ Leiningen J Buildr ,

• https://mvnrepository.com/artifact/io.bitbucket.kefir666/ECLib - - > 

io.bitbucket.kefir666

ECLib

l.9.0

Рисунок 3. Информация об опубликованном артифакте.

Figure 3. Information about the published artifact.

ОБСУЖДЕНИЕ

Посмотрим на результаты исследования, касающиеся производительности ECDSA (см. рисунок 2). На кривых P-256 и P-384 оба подхода демонстрируют примерно одинаковую производительность (с разницей, которая достигает до 3 миллисекунд), однако на кривой P-512 мы наблюдаем явное преимущество использования java.security, с выигрышем до 15 миллисекунд. Можно предположить, что это связано с применением особенностей обобщенных чисел Мерсенна [12], которые позволяют эффективно выполнять модулярные операции. Этот факт дает мотивацию к дальнейшим доработкам библиотеки.

В пакете java.security имеется класс Signature, предназначенный для работы с электронной цифровой подписью. Для использования ECDSA возможно задать алгоритм через параметр algorithm (например, SHA256withECDSA). Кривая может быть выбрана с помощью класса ECGenParameterSpec, где параметры кривых определены в соответствующей документации. Это означает, что определение собственных параметров для кривой может представлять проблему. С одной стороны, это обеспечивает защиту пользователя, не обладающего достаточными знаниями в криптографии, от выбора небезопасной кривой. Однако, с другой стороны, это ограничивает гибкость в выборе кривой. В данной библиотеке есть возможность использования кривых с пользовательскими параметрами, однако они сначала должны пройти валидацию (может произойти вызов исключения).

ЗАКЛЮЧЕНИЕ

Разработанная криптографическая библиотека для работы с эллиптическими кривыми может быть использована в качестве средства для изучения свойств различных эллиптических кривых, а также в качестве средства обеспечения информационной безопасности. В дальнейшем в библиотеку возможно добавление алгоритма EdDSA (ЭЦП на основе кривых Эдвардса), а также методов генерации параметров случайных кривых: например, при помощи алгоритма Шуфа или метода комплексного умножения. Стоит отметить, что созданный продукт удобен в плане подключения его к другим проектам (подключение зависимости при помощи Apache Maven), а также предоставляет пользователям возможность выбора различных алгоритмов скалярного умножения, координатного представления точки, а также пользовательской кривой в алгоритмах электронной цифровой подписи.