Эффект пластичности стекол в модели делокализованных атомов

Природа деформации стеклообразных твердых тел на протяжении многих лет является предметом всесторонних исследований. Интерес к этой проблеме обусловлен прежде всего широким применением на практике различных классов стекол и в связи с обнаружением у них значительной остаточной деформации (пластичности) [1–5].

Эффект пластичности неорганических стекол был обнаружен, по-видимому, Гелафом Г. и Томасом И. [1] в 1926 г. при микровдавливании силикатного стекла алмазной пирамидкой, а систематически был исследован впервые Бриджменом П. и Сименом И. [2]. Опыты показали, что у неорганических стекол при 200C наблюдаются большие неупругие остаточные деформации, если механическое внешнее напряжение превышает некоторый порог σy, который для силикатных стекол по порядку величины совпадает с микротвердостью по Виккерсу HV. Та- ким образом, при σ > σy обнаруживается остаточная деформация стекол, которая сохраняется неопределенно долго (эффект пластичности стекол).

Однако примечательно то обстоятельство, что при нагревании ниже температуры стеклования T g и вблизи нее данная деформация релаксирует практически до исчезновения [2]. Следовательно, она оказывается на самом деле замороженной обратимой деформацией. Тем не менее, как принято в научной литературе, будем пользоваться термином «пластическая» и величину σ y будем называть пределом текучести.

Аналогичная обратимая замороженная (пластическая) деформация наблюдается у аморфных органических полимеров в стеклообразном состоянии (старые названия: «холодное течение», «вынужденно-эластическая деформация») [3, 4]. У массивных металлических стекол также обнаружены замороженная деформация и ее термостимулированная релаксация, основные закономерности которых фактически такие же, как и у стеклообразных органических полимеров и неорганических стекол [5]. Как видим, данное явление носит универсальный характер. Замороженная деформация стекол и ее термостимулированная релаксация по внешним проявлениям напоминают пластическую деформацию кристаллов и ее последействие. Однако из опытных данных следует, что пластичность стекол по природе принципиально отличается от пластичности кристаллов.

Настоящий обзор посвящен рассмотрению основных закономерностей и природы пластической деформации стеклообразных твердых тел и ее термостимулированной релаксации. При этом проводится сравнение этой деформации с размягчением стекла — с процессом, обратным стеклованию, что позволяет получить определенную информацию как о пластической деформации стекол, так и о переходе жидкость — стекло. Установлено, что существует определенная взаимосвязь между размягчением стекла и пластической деформацией стекол. Так, например, у ряда аморфных полимеров и неорганических стекол обнаружена линейная корреляция между пределом текучести σ y и температурой стеклования T g (температурой размягчения). Основные закономерности как стеклования, так и пластической деформации у аморфных веществ удовлетворительно описываются в рамках одной модели — модели делокализованных атомов, развиваемой в Бурятском государственном университете [6–10].

Как и в случае универсальности эффекта пластичности стекол, основные закономерности процесса стеклования в качественном отношении оказываются также универсальными для различных аморфных веществ независимо от их природы. Об этом свидетельствует наличие универсальных уравнений и правил в области стеклования [11–15].

Особенность обзора заключается в том, что, во-первых, эффект пластичности стекол рассматривается в тесной связи со стеклованием расплава. Во-вторых, уделено особое внимание совместному рассмотрению с единых позиций различных классов стеклообразных систем: неорганических стекол, аморфных органических полимеров, металлических аморфных сплавов. Кроме того, в-третьих, предлагается развитие универсальной модели аморфных веществ.

В обзоре кратко анализируются различные подходы к интерпретации пластической деформации стекол [10, 11, 16–27]. Более подробно рассматривается применение указанной выше модели.

Насколько нам известно, в научной литературе нет подобного обзора эффекта пластичности стекол.

2.    Эффект пластичности неорганических стекол

Бриджмен и Симон [2] установили, что при всестороннем, а также при одноосном сжатии стеклообразного борного ангидрида в твердом состоянии ниже температуры стеклования Tg ≈ 2500С наблюдается остаточная неупругая дефор- мация, которая после разгрузки сохраняется в течение неопределенно долгого времени. Однако, при нагревании неупруго деформированного стекла в интервале 20-1000C восстанавливается его первоначальное исходное состояние. Следовательно, данная деформация оказывается не остаточной, а замороженной обратимой деформацией.

Они оценили энергию активации процесса термостимулированного возврата первоначального состояния стеклообразного борного ангидрида в указанном ин- тервале температур по соотношению

U = R

к

T 1

—

к-1

т

± 2 У

ln ^{v 2} v₁

(2.1)

где R — газовая постоянная, v 1 и v 2 — начальные скорости уменьшения остаточной деформации при температурах T 1 и T 2 . Для энергии активации было получено удивительно низкое значение: U = 5.5 кДж/моль. Хотя, как заметили авторы, эта оценка является приближенной, малая величина U указала на необычную природу пластичности стекол.

После опытов Бриджмена и Симона эффект пластичности неорганических стекол изучался многими исследователями [28-32]. Более подробные систематические измерения в этом направлении провел Маккензи [31, 32], который показал, что пластичность стекол проявляется как при одноосном, так и при всестороннем сжатии, при микровдавливании алмазной пирамидки, при растяжении тонкой стеклянной нити (волокна).

Таким образом, если механическое внешнее напряжение превышает некоторый порог — предел текучести σ y , происходит пластическая деформация стекол, которая при 20⁰С сохраняется сколь угодно долго. Однако, при нагревании ниже температуры стеклования T g и вблизи нее она релаксирует до исчезновения.

У силикатных стекол предел текучести составляет около бу ~ 500 кгс/мм2(5^104 атм), (2.2)

что по порядку величины совпадает с микротвердостью по Виккерсу H V . У этих стекол температурная зависимость скорости обсуждаемой деформации и скорости ее термостимулированной релаксации является экспоненциальной и их энергия активации примерно равна

AU « 20 кДж/моль, (2.3)

что резко отличается от энергии активации процесса вязкого течения ( ~ 400 кДж/моль) и диффузии иона кислорода ( ~ 250 кДж/моль) в силикатных стеклах. Следовательно, пластическая деформация и ее термостимулированная релаксация относятся к низкоактивационным релаксационным процессам.

3.    Исследование пластичности стекол методом наноиндентирования

При вдавливании четырехгранной алмазной пирамидки Виккерса в силикатное стекло при 20 ° С образуется пластическая лунка — микроотпечаток (рис. 3.1, вид сверху). При этом микротвердость по Виккерсу H V у силикатных, германат-ных и других неорганических стекол совпадает с пределом текучести H v ® с у , выше которого наблюдается пластическая деформация [33, 34].

Как и следовало ожидать, при нагревании (ниже T g ) микроотпечаток уменьшается — наблюдается релаксация пластической деформации (рис. 3.1). Энергия активации этого процесса у силикатных стекол составляет ~ 20 кДж/моль [11], что совпадает с энергией активации уплотнения и разуплотнения силикатных стекол при сжатии (2.3).

При внедрении в стекло заостренного индентора напряженное состояние локализуется в достаточно малом микрообъеме, линейные размеры которого меньше среднего расстояния между дефектами. Поэтому на результат измерения микротвердости не влияют дефекты (поверхностные микротрещины) [11].

Было показано [35-38], что под индентором возникает локальная деформация сдвига и что микротвердость H V , рассматриваемая как среднее нормальное напряжение, на самом деле определяется максимальным касательным (тангенциальным) напряжением и служит характеристикой сопротивления материала сдвигу.

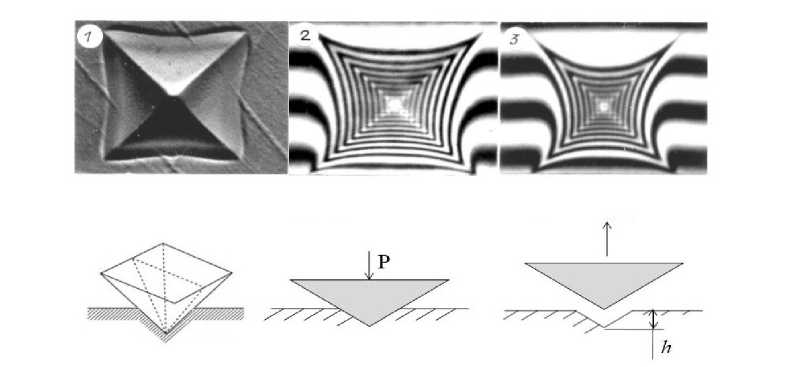
Рис. 3.1. Микроотпечатки Виккерса на листовом силикатном стекле: 1 — при T = 20 ° C; 2, 3 — виды в интерференционном микроскопе после нагрева, соответственно при T = 100 ° C, T = 450 ° C в течение 10 мин; P = 150 г., T g = 620 ° C.

В серии работ [11, 39–56] исследована кинетика термостимулированного восстановления микроотпечатков Виккерса и микроканавок на листовом силикатном стекле.

4.    Пластичность стеклообразных полимеров

В первой половине XX века у аморфных органических полимеров в стеклообразном состоянии выше некоторого предельного механического напряжения σ у была обнаружена большая остаточная деформация, которая получила название

«холодное течение». Александровым, Лазуркиным и Фогельсоном были проведены первые систематические исследования [3, 4, 57]. Оказалось, что пластически деформированные стеклообразные аморфные полимеры при термостимулировании (нагревании) возвращаются к исходному недеформированному состоянию. Таким образом, было установлено, что «холодное течение» представляет собой не остаточную деформацию, а замороженную обратимую деформацию полимерных стекол.

Чтобы подчеркнуть принципиальное различие в механизмах возникновения больших остаточных деформаций в стеклообразных полимерах и металлах, будущий академик (Председатель Президиума АН СССР в 1980-1990-ые годы) Александров А.П. в 1945 г. предложил термин «вынужденно-эластическая деформация» [3]. Величина σ у получила название «предела вынужденной эластичности». Было развито представление, что переход цепных полимерных макромолекул из одного локального равновесного состояния в другое становится возможным лишь при значительном вынуждающем действии внешних напряжений. В свою очередь вынужденная высокоэластическая деформация после снятия напряжения остается фиксированной, так как тепловое движение при низких температурах оказывается ослабленным и не способно вернуть громоздкие макромолекулы к первоначальной конфигурации. Лишь при нагревании возникает необходимая подвижность макромолекул и деформация полностью самопроизвольно восстанавливается (исчезает) [3, 57].

В настоящее время несостоятельность такой «полимерной» концепции стала очевидной [58-64], ибо такие же большие остаточные деформации наблюдаются у низкомолекулярных органических и неорганических стекол, даже у металлических стекол, где нет никаких громоздких макромолекул.

Стеклообразные органические полимеры являются типичными представителями неупорядоченных некристаллических твердых тел и имеют такие же физико-механические характеристики, как и у всех стеклообразных систем. Поэтому следует ожидать, что природа замороженной обратимой деформации должна быть одинаковой как у высокомолекулярных, так и у низкомолекулярных стекол.

5.    Пластическая деформация массивных металлических стекол

Металлические стекла (МС) получают сверхбыстрой закалкой (резким охлаждением) расплава металла, поэтому они являются сильно неравновесными структурами. Удивительно то, что они оказались достаточно устойчивыми системами. Начиная с 1970-х годов и в течение последующих примерно 30 лет МС получали в виде ленты толщиной 20 40 мкм методом, обеспечивающим требуемую для стеклования скорость охлаждения ~10⁶ К/с. В конце 1990-х годов удалось создать металлические композиции, допускающие стеклование даже при скоростях закалки 1 ^ 10 -1 К/с [65, 66]. При этом стало возможным получение МС толщиной 1 см и более. Такие стекла стали называть массивными.

Важнейшей особенностью массивных металлических стекол, в отличие от стандартных ленточных МС, является большая разница между температурой стеклования и температурой кристаллизации, что позволяет проводить термообработку выше Т g . Это не только существенно расширило диапазон экспериментов, но и открыло возможности, нереализуемые в случае ленточных МС.

Ранее на примерах ленточных МС было принято считать, что неупругая деформация МС при 20⁰C ниже T g является необратимым процессом. Однако Хо-ник с соавторами [5, 67] показали, что при термостимулировании вблизи и выше Т g полностью восстанавливается (исчезает) неупругая деформация массивных металлических стекол. Следовательно, она оказывается замороженной обратимой деформацией, как и у других стекол.

Далее перейдем к обсуждению природы пластической (замороженной обратимой) деформации стеклообразных систем.

6.    Различные подходы к природе пластической деформации стеклообразных твердых тел

Для объяснения эффекта пластичности стекол предложены различные подходы [3, 4, 11, 18, 19-27, 34]. По мнению многих исследователей он связан с зарождением под напряжением специфических мелкомасштабных дефектов — элементарных сдвигов, получивших названия: «дислокации Сомилианы», «незавершенные сдвиги», «пластические сдвиговые трансформации». В последнее время они получили общее название «сдвиговых трансформаций» [20, 23]. Они образуются в малых объемах стекла и создают локальную пластическую деформацию. Их накопление ведет к появлению остаточных макроскопических пластических деформаций.

Олейник с соавторами [16, 68, 69] провели систематические исследования термодинамики неупругой деформации стеклообразных органических полимеров. Измерения проводили при комнатной температуре в режиме одноосного сжатия. Оказалось, что запасание энергии стеклами начинается сразу же за гуковской упругостью. На ранних стадиях неупругой деформации 100% работы внешних сил переходит во внутреннюю энергию образца.

Для сравнения в сходных условиях проведены такие же измерения для монокристалла меди. Для него наблюдается совершенно другая ситуация: сразу за гуковской упругостью практически вся внешняя работа рассеивается в виде деформационной теплоты. Такая разница в термодинамическом поведении стекол и меди свидетельствует о принципиальном различии в механизмах деформации кристаллов и стекол.

Сравнение начальных (ранних) и последующих после зуба текучести стадий деформации стеклообразных полимеров показывает, что с самого начала появления неупругого отклика материала главным контролирующим общую кинетику деформации механизмом процесса является зарождение сдвиговых трансформаций структуры. Именно зарождение и накопление таких трансформаций ответственно за рост внутренней энергии в ходе деформирования. Негуковскую, но обратимую при термостимулировании составляющую деформации называют запаздывающе- упругой, нелинейно-упругой или последействием. Мы пользуемся термином «замороженная обратимая деформация».

В кристаллах основными элементарными носителями пластической деформации являются специфические дефекты — так называемые краевые дислокации, которые являются линейными дефектами кристаллической решетки. Деформационное тепло в кристаллах появляется при скольжении этих дислокаций вдоль линии скольжения из-за трения о решетку. В стеклах нет таких дефектов — дислокаций и нет линий скольжения из-за отсутствия дальнего порядка.

Опыты показывают [68], что вся энергия, запасенная в деформированном стекле, выделяется при нагревании ниже Т g в стеклообразном состоянии.

Стеклообразное твердое тело, накапливая такие структурные перестройки как локальные сдвиговые трансформации, при деформации переходит в состояние с повышенной энергией. Естественно, что при разгрузке это состояние стремится исчезнуть, а структура возникших сдвиговых трансформаций — отрелак-сировать к исходному, недеформированному состоянию, скорость такой релаксации определяется барьером возврата. Ясно, что сдвиговые трансформации, возникшие при малых напряжениях σ, рождаются сравнительно легко и локальные перестройки структуры тела при образовании таких сдвиговых трансформаций незначительны. Согласно Олейнику с соавторами [68, 69], именно это свойство сдвиговой трансформации делает барьер возврата локальной деформированной структуры низким, сравнимым с энергией теплового движения kT деф . Эти «слабые» сдвиговые трансформации ответственны за процесс запаздывающей упругости — за процесс термостимулированной релаксации пластической деформации стекол. Этот факт согласуется с низкой энергией активации пластической деформации силикатных стекол.

Таким образом, Олейник с соавторами [16, 23, 24] последовательно развивают представление о том, что пластическая деформация и ее термостимулированная релаксация протекают не в исходной, а в иной структуре, возникающей в процессе деформации. Локальные сдвиговые трансформации возникают под действием внешнего напряжения и исчезают при нагревании ниже и вблизи T g .

Луковкин и Аржаков [25] считают, что пластичность стекол является следствием исходной структурной неоднородности аморфных систем. Предполагается, что пластическая деформация связана с последовательным размягчением структурных микрообластей, характеризующихся локальными температурами размягчения. Тем самым они допускают тесную взаимосвязь между замороженной обратимой деформацией стекол и их размягчением при нагревании — процессом, обратным стеклованию.

Интересно отметить, что пластическая деформация стекол вполне удовлетворительно описывается формально с помощью математического аппарата дислокационной теории пластичности кристаллов [19, 21]. Однако до сих пор не найдены в стеклообразных телах дефекты, подобные краевой дислокации, которая, как отмечалось выше, является дефектом кристаллической решетки. А в стеклах нет такой решетки. Тем не менее, дислокационная аналогия несомненно заслуживает внимания.

В Бурятском государственном университете развито представление о том, что элементарным актом пластической деформации стекол служит делокализация атома — предельное его смещение из локального равновесного положения [10, 34]. Делокализация атома обусловлена флуктуацией ближнего порядка аморфного вещества (перегруппировкой соседних частиц) и отражает локальное конфигурирационное изменение структуры. Концентрация делокализованных атомов довольно сильно (экспоненциально) зависит от температуры и механического напряжения [6, 7, 15]. В направлении действия механического напряжения концентрация делокализованных атомов возрастает. Важным параметром модели делокализованных атомов является флуктуационный объем аморфного вещества, обусловленный делокализацией атомов. Приложение этой модели к пластичности стекол подробно рассмотрено в разделе 7. По-видимому, делокализацию атома можно рассматривать как некоторый аналог локальной сдвиговой трансформации. В частности, из этой модели следует, что пластическая деформация стеклообразных материалов обратно пропорциональна параметру Грюнайзена — мере ангармонизма колебаний решетки и нелинейности силы межатомного взаимодействия. К такому же заключению приводит фононная концепция пластичности стекол (разделы 7.6 и 8).

За рубежом появилась серия публикаций, посвященных проблеме пластичности стекол (см., например, работы [18, 20, 70, 71]). Представляет интерес работа Benzine с соавторами [18], где локальную пластичность стеклообразных систем сравнивают с другим универсальным для стекол явлением, а именно наличием в спектрах комбинационного рассеяния света (КР) низкочастотного, так называемого бозонного пика, который связывают с радиусом корреляции неупорядоченной структуры жидкостей и стекол R c = υ s /ω max , где υ s — скорость звука, ω max — частота, соответствующая данному пику⁷². Прослеживается определенная связь между параметрами модели делокализованных атомов и характеристиками низкочастотного бозонного пика в спектре КР, в частности, между энергией делокализации атома Δε e и частотой максимума ω max : Δε e = Ch ω max , где C — коэффициент пропорциональности, h — постоянная Планка. Так, линейная корреляция между ω max и T g [72] находится в согласии с корреляцией между Δε e и T g (раздел 7). Бозонный пик у силикатных стекол характеризуется низкой энергией активации ∼ 20 кДж/моль, близкой к Δε e . Относительное число делокализованных атомов определяется по формуле, которая по внешнему виду совпадает с известным соотношением Бозе–Эйнштейна при Δε e = hν (например, формула (13.8) в работе [15]).

На основе теории свободного объема, развитой для процесса стеклования, удалось установить связь между пределом текучести и релаксацией объема аморфных полимеров в процессе отжига ниже температуры стеклования. Показано, что один и тот же термически активированный процесс контролирует как пластическую деформацию, так и структурную релаксацию. Оказывается, что молекулярные параметры, в частности, энергия образования дырки, входящие в теорию стеклования, успешно используются при описании поведения предела текучести в зависимости от скорости охлаждения, времени отжига, температуры и скорости деформации [70].

В целом необходимо отметить, что природа эффекта пластичности стекол остается до конца нерешенной проблемой.

7.    Применение модели делокализованных атомов к пластической деформации стеклообразных твердых тел

В молекулярно-кинетических процессах, протекающих в жидкостях и аморфных веществах, важную роль играет элементарный механизм, обусловленный делокализацией атома — его предельным смещением из локального равновесного положения [6–10]. Как отмечено выше, делокализация атома обусловле- на флуктуацией ближнего порядка и, по существу, отражает локальное конфигурационное структурное изменение.

• 7.1.    Стеклование жидкости и делокализация атома

В силикатных стеклах делокализация атома представляет собой предельное смещение мостикового атома кислорода в мостике Si-O-Si, связанное с локальной низкоактивационной деформацией кремнекислородной сетки [7]. Полагаем, что делокализация атома служит необходимым условием реализации элементар- ного акта процесса вязкого течения неорганических стекол, например, переключения валентной связи по Мюллеру Р. Л. [11], а также образования флуктуационной дырки по Френкелю Я. И. [73] в случае вязкого течения простых жидкостей.

Без делокализации атома («пускового механизма» текучести) невозможно вязкое течение. Поэтому замораживание процесса делокализации активного атома в области стеклования приводит к прекращению вязкого течения и к переходу расплава в стеклообразное состояние. Этот момент наступает тогда, когда энергия тепловых колебаний решетки, отнесенная к атому, становится равной или меньше энергии делокализации атома: (i/2)kT < Аве, что приводит к следующему условию перехода жидкость — стекло

-kT„ = Ае,(7.1)

2ge где i — число степеней свободы кинетической единицы, ответственной за стеклование, Tg — температура перехода.

Энергия делокализации атома

Ае e = Pi Ave(7.2)

тесно связана с предельной упругой деформацией связи между атомами, и она равна работе предельного смещения атома, совершаемой против внутреннего давления pi, обусловленного силами межатомного (межмолекулярного) притяжения. Здесь Ave — элементарный флуктуационный объем, необходимый для смещения атома (объем делокализации атома) [6, 7]: Ave = п dA rm, п d — площадь эффективного сечения атома, Δrm — предельное смещение атома из локального равновесного положения.

Как и следовало ожидать, в соответствии с критерием (7.1) энергия A v e , определенная независимым способом ( R – газовая постоянная),

A v e = RD, (7.3)

для силикатных, германатных и боратных стекол [9] линейно зависит от температуры стеклования T g (рис. 7.1, 7.2). Здесь D — эмпирический параметр уравнения Енкеля [74, 75]

П = A exp

B

+

T

C y- exP|

D

T

(7.4)

успешно описывающего температурную зависимость вязкости η(T) стеклообразующих жидкостей в широком интервале температур. У сульфатно-фосфатных стекол NaPO s -MeSO 4 (Me = Li, Na, K) между энергией делокализации атома Ае e и температурой стеклования T g наблюдается также линейная корреляция (рис. 7.3). Величина Ае e рассчитана по формуле (табл. 7.1)

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА

Ae e = Rc,

(7.5)

где с — эмпирическая постоянная в уравнении Брэдбури — Шишкина [76, 77]

П = П о exP

a expl

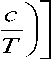
(7.6)

которое описывает зависимость n ( T) в области стеклования.

При выводах уравнений вязкости (7.4) и (7.6) в рамках модели делокализованных атомов и активационной теории вязкости величины RD и Rc приобретают смысл энергии делокализации атома Ae e [7, 15, 78, 79].

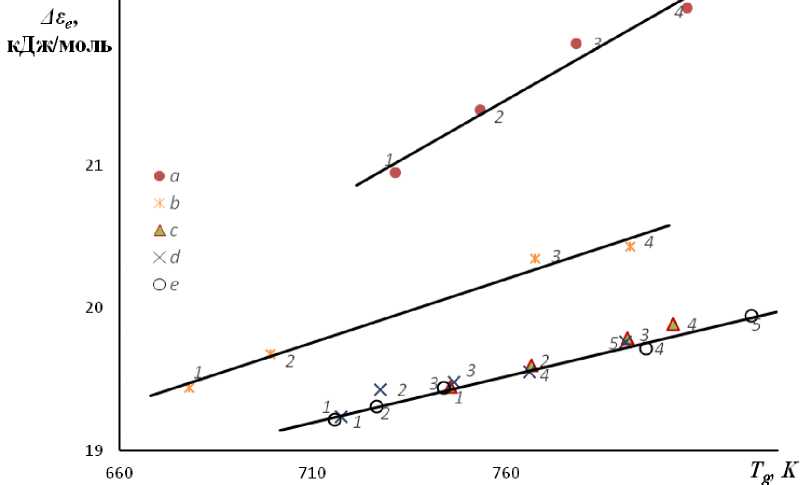
Рис. 7.1. Линейная корреляция между энергией делокализации атома Δε e = RD и температурой стеклования T g для силикатных и германатных стекол.

D — параметр уравнения Енкеля (7.4). a — GeO 2 –Na 2 O (содержание Na 2 O, мол. %: 1 — 30, 2 — 25, 3 — 20, 4 — 15); b — SiO 2 –PbO (PbO, мол. %: 1 — 50, 2 — 45, 3 — 30, 4 — 24,6); c — SiO 2 –K 2 O (K 2 O, мол. %: 1 — 25, 2 — 20, 3 — 15, 4 — 13); d — SiO 2 –Na 2 O (Na 2 O, мол. %: 1 — 33, 2 — 30, 3 — 25, 4 — 20, 5 — 15); e — SiO 2 –Li 2 O (Li 2 O, мол. %: 1 — 33,3, 2 — 30, 3 — 25, 4 — 14, 5 — 10).

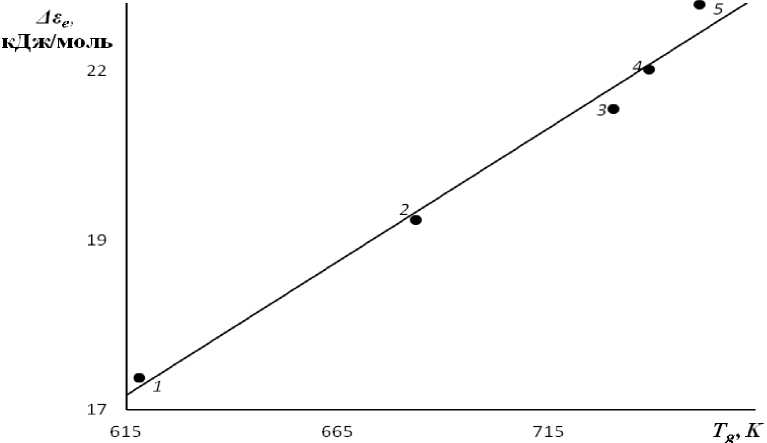
Рис. 7.2. Зависимость энергии делокализации атома Δε e = RD от температуры стеклования T g для натриевоборатных стекол Na 2 O–B 2 O 3 . D — параметр уравнения Енкеля (7.4).

Содержание Na 2 O, мол.%: 1 — 10, 2 — 15, 3 — 20, 4 — 25, 5 — 30.

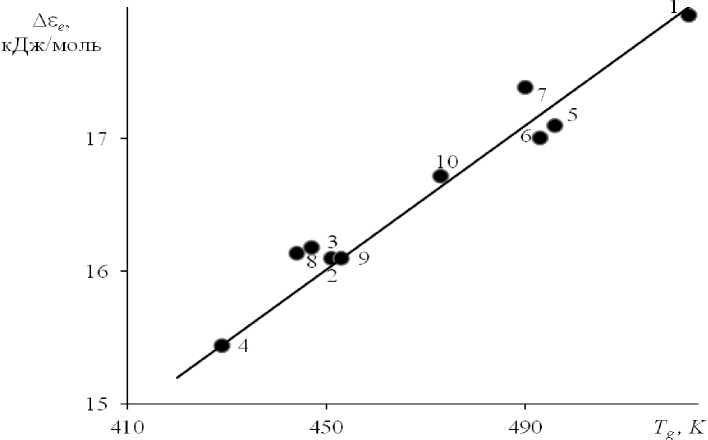
Рис. 7.3. Корреляция между энергией делокализации атома ∆εe и температурой стеклования Tg сульфатно-фосфатных стекол. 1 — NaPO3, NaPO3–Li2SO4, содержание Li2SO4, мол.%: 2 — 10, 3 — 20, 4 — 30; NaPO3–Li2SO4, содержание Na2SO4, мол.%: 5 — 10, 6 — 20, 7 — 30; NaPO3–K2SO4, содержание K2SO4, мол.%: 8 — 10, 9 — 20, 10 — 30.

Таблица 7.1

Свойства сульфатно-фосфатных стекол NaPO 3 -MeSO 4 (Me=Li, Na, K) и параметры модели делокализованных атомов (использованы данные [101]). a и c — параметры уравнения (7.6).

№	Стекло	T g , K	E, кгс мм2	µ	a	c, K	f g	∆ɛ e , кДж/моль		A v e , = 3 A
								(7.5)	(7.9)
1	NaPO 3	523	3610	0.294	0.99	2160	0.016	17.9	17.9	16
2	0.9 NaPO 3 — 0.1 Li 2 SO 4	451	4140	0.300	0.97	1940	0.014	16.0	16.1	13
3	0.8 NaPO 3 — 0.2 Li 2 SO 4	447	4210	0.303	0.95	1950	0.013	16.1	16.2	14
4	0.7 NaPO 3 — 0.3 Li 2 SO 4	429	4230	0.034	0.95	1860	0.014	15.2	15.4	11
5	0.9 NaPO 3 — 0.1 Na 2 SO 4	496	3730	0.299	0.97	2060	0.016	17.0	17.1	14
6	0.8 NaPO 3 — 0.2 Na 2 SO 4	493	3550	0.292	0.96	2050	0.016	16.9	17.0	15
7	0.7 NaPO 3 — 0.3 Na 2 SO 4	490	3540	0.288	0.95	2095	0.015	17.1	17.4	16
8	0.9 NaPO 3 — 0.1 K 2 SO 4	444	3380	0.316	0.95	1945	0.013	16.0	16.1	16
9	0.8 NaPO 3 — 0.2 K 2 SO 4	453	3350	0.316	0.96	1940	0.014	16.0	16.1	15
10	0.7 NaPO 3 — 0.3 K 2 SO 4	473	3340	0.313	0.99	2015	0.014	16.8	16.7	16

В результате делокализации (тепловых смещений) атомов в жидкостях и аморфных твердых телах возникает флуктуационный объем

∆V s = N s ∆v s , где N e — число делокализованных атомов.

У неорганических стекол, металлических аморфных сплавов, аморфных органических полимеров и низкомолекулярных органических стекол доля флуктуационного объема f g , замороженная при температуре стеклования T g , слабо зависит от природы стекол (табл. 7.2)

f = (^A V e )    » 0.025 ^ 0.030.                   ^(7.8)

g I V ) t = T g

У стекол одного типа она практически постоянна. Например, у натриевоси-ликатных стекол: f g ® const = 0.028 (табл. 7.2). Величина f g определяется по данным о вязкости в области стеклования [7, 8]. У сульфатно-фосфатных стекол значения f g меняются также в небольших пределах ( f g ® const ), однако заметно ниже, чем у силикатных стекол (табл. 7.1). Доля флуктуационного объема f g входит в формулы модели делокализованных атомов (например, (7.9)).

Таблица 7.2

Параметры уравнения Вильямса-Ландела-Ферри (ВЛФ) C 1 , C 2 и доля флуктуационного объема f g , замороженная при температуре стеклования T g [6, 7]

Аморфное вещество	T g , К	C 1	C 2 , К	f g	ln(1 / f g )	Δε e , кДж/моль
Натриевосиликатные стекла Na 2 O–SiO 2
Na 2 O, мол. %
15	782	36	430	0.028	3.6	23
20	759	36	390	0.028	3.6	23
25	739	35	355	0.028	3.6	22
30	721	35	322	0.028	3.6	22
33	712	35	304	0.028	3.6	21
35	705	35	291	0.028	3.6	21
Металлические стекла (аморфные сплавы)
Pd 40 Ni 40 P 20	602	39	93	0.026	3.6	18
Pt 60 Ni 15 P 25	500	37	95	0.027	3.6	15
Pd 77.5 Cu 6 Si 16.5	653	38	100	0.026	3.6	19
Fe 80 P 13 C 7	736	38	120	0.026	3.6	22
Аморфные органические полимеры и селен
Поливинилацетат	305	36	47	0.028	3.6	9
Натуральный каучук	300	38	54	0.026	3.6	9
Метакрилат этиловый	335	40	65	0.025	3.6	10
Селен	303	32	58	0.031	3.5	9
Низкомолекулярные органические стекла
Пропанол	98	41	25	0.024	3.7	3
Протиленгликоль	160	44	40	0.023	3.8	5
Глицерин	185	42	53	0.024	3.7	6

Примечание: уравнение ВЛФ: ln a t = — C i ( T — T g )/( T — T g + C 2 ), a ? = n ( T )/ n ( T g ), f g =1/ C 1 , Ae e = RT g ln(1 f g ).

Предполагаем, что вязкое течение расплавов неорганических стекол выше T g наряду с другими причинами реализуется главным образом за счет возбужденных делокализованных мостиковых атомов с энергией возбуждения Av e . У ще-лочносиликатных стекол эта энергия составляет около (табл. 7.2) [6, 7]

Ав е ~ RT g ln(1/f g ) ® 20 кДж/моль

(7.9)

Расчет энергии делокализации атома по формуле (7.3) из данных об эмпирической постоянной D = 2500 K (табл. 7.3) [75] для щелочносиликатного стекла

Ав е = RD = 21 20 кДж/моль находится в согласии с результатами расчета по уравнению модели делокализованных атомов (7.9).

Таблица 7.3.

Эмпирические постоянные уравнения Енкеля (7.4) и вычисленные из них характеристики вязкого течения и стеклования аморфных веществ (Δ F ∞ = RB и Δε e = RD )

Вещество	B \	D	Δ F ∞ 1 Δ ε e		Литература
	К		кДж/моль
Силикатное стекло
№15	13226	2500	110	21	[75]
№18	13348	2500	111	21	[75]
Na 2 O 3SiO 2	-	1840	-	15	[74]
Минеральное масло:
XII	1195	800	10	7	[75]
XIII	928	700	8	6	[75]
XIV	741	600	6	5	[75]
XV	686	600	6	5	[75]
XVI	615	600	5	5	[75]
Глицерин	-	920	-	8	[74]
Полиизобутилен	-	460	-	4	[74]

Примечание: Δ F ∞ — высокотемпературный предел свободной энергии активации вязкого течения стеклообразующих жидкостей.

Обращает внимание то обстоятельство, что энергия делокализации атома Δε e по порядку величины сравнима со средней энергией теплового колебательного движения решетки в области стеклования. Последняя, например, по закону равнораспределения энергии по степеням свободы (согласно классическому выражению Δε D = 3 N A kT = 3 RT ) для силикатных стекол, у которых T g ≈ 700–900 K , составляет около:

∆ɛ D = 3RT g ≈ 17-22 кДж/моль

Таким образом, в рамках развиваемых представлений стеклование жидкости связано с замораживанием процесса делокализации атома. Из рис. 7.1–7.3 следует, что у исследованных стекол энергия делокализации атома Δε e линейно зависит от температуры стеклования.

7.2.    Линейная корреляция между пределом текучести и температурой стеклования в модели делокализованных атомов

Представление о том, что элементарный акт пластической деформации стекол сводится к делокализации атома (кинетической единицы), находится в удовлетворительном согласии с экспериментальными данными: расчеты предела текучести и энергии активации этой деформации согласуются с экспериментом [34]. Энергия активации пластической деформации силикатных стекол Δ u ≈ 20 кДж/моль совпадает с энергией делокализации атома в них Δ u ≈ ∆ɛ e .

Как и следовало ожидать, внутреннее давление неорганических стекол, против которого совершается работа делокализации атома, совпадает с микротвердостью этих систем HV — с пределом текучести σу ≅ HV, выше которого наблюдается пластическая деформация. Было показано, что для 79 силикатных, герма- натных и фосфатных стекол величина pi практически совпадает с их микротвердостью по Виккерсу pi ≅ HV [33]. С этих позиций внутреннее давление этих стекол может служить мерой предела текучести pi ≈ σу.

Предел текучести σy имеет смысл напряжения, необходимого для критического смещения (делокализации) кинетической единицы. Как следует из приведенных выше соображений, по величине σy совпадает с внутренним давлением pi =Δεe / Δve, против которого совершается работа делокализации атома. Принимая во внимание равенство σy = pi и подставив в это отношение энергию делокализации атома Δεe (7.9), приходим к следующей связи между пределом текучести σy и температурой размягчения (температурой стеклования) Tg k ln(1/fg )

(7.19)

σ =            T ^.

y      A v e     ^g

Как мы уже знаем, в качестве кинетических единиц, способных к делокализации, в неорганических стеклах выступают мостиковые «шарнирные» атомы типа мостикового атома кислорода в мостике Si-O-Si. Поэтому объем делокализации атома Δv e у стекол одного класса фактически одинаков: Δv e ≈ const [6, 7].

В соответствии с формулой (7.19) при f g ≈ const и Δv e ≈ const для стекол одного типа должна наблюдаться линейная корреляция между величинами σ y и T g , а также между H V и T g . В самом деле, у аморфных полимеров между σ y и T g обнаруживается линейная корреляция (рис. 7.4) [34]. Как видно из рис. 7.5 и 7.6, микротвердость (предел текучести) ряда стекол также линейно зависит от температуры стеклования T g [11, 80, 81].

Таким образом, данный подход дает один из вариантов объяснения наличия линейной корреляции между пределом текучести и температурой размягчения стекол.

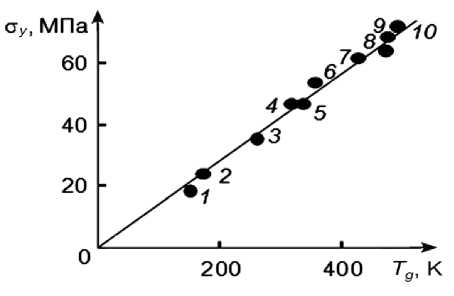
Рис. 7.4. Линейная корреляция между пределом текучести σ y и температурой стеклования T g аморфных полимеров. 1 — политетрафторэтилен, 2 — полиэтилен, 3 — полипропилен, 4 — полиамид, 5 — полиэтилентерефталат, 6 — поливинилхлорид, 7 — поликарбонат, 8 — полиарилатсульфон, 9 — полисульфон, 10 — полиарилат.

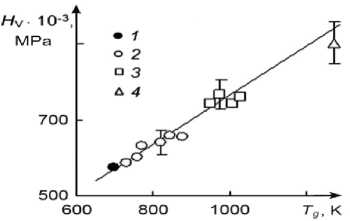
Рис. 7.5. Корреляция между микротвердостью H V и температурой стеклования силикатных стекол. 1 — свинцовосиликатное, 2 — щелочносиликатные, 3 — алюмосиликатные, 4 — кварцевое

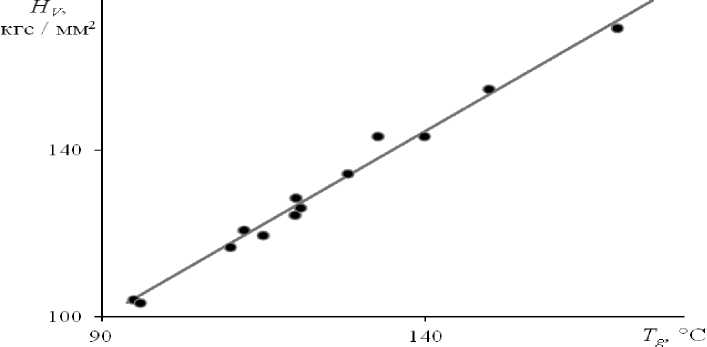
Рис. 7.6. Линейная корреляция между H V и T g для бескислородных халькогенидных стекол системы мышьяк-теллур-алюминий при различных содержаниях компонентов [80]

7.3. Зависимость скорости термостимулированной релаксации пласти-

ческой деформации стекол от температуры и давления

Скорость восстановления пластически деформированных стеклообразных

полимеров при нагревании v rel как функция температуры и давления подчиняется

следующей экспоненциальной зависимости [82]

vr=l = A exP l

A u + p A v y kT

.

(7.20)

Для эпоксидного сеточного аморфного полимера получено значение активационного объема данного релаксационного процесса, равное [82]

∆v у = (55 ± 8)ų                                 (7.21)

В модели делокализованных атомов скорость термостимулированного восстановления исходного недеформированного состояния стекла (7.20) определя- ется скоростью изменения числа делокализованных атомов в данном процессе νrel~ (dNe/dt), откуда зависимость (7.20) выводится из уравнения модели для относительного числа делокализованных атомов [6]

N e- = ex/ - ^{А в} ' ⁺ p ^{A v} ' ) .                  (7.22)

N   \   kT  )

Активационный объем A v у получает следующую трактовку: A v у = A v e . У сетчатых эпоксидных полимеров типа модифицированной эпоксидной смолы ЭД-16 значения объема делокализации атома A v e , рассчитанные по формуле модели (7.15) [6]:

3(1 - 2ц) kT          ° ³             _п

A v„ = —---- g * 45 ^ 74 A ,             ⁽⁷-²³⁾

е        fgE                    , имеют такой же порядок величины, что и приведенное выше значение активационного объема Avу. Для указанных эпоксидных полимеров для расчета Ave приняты данные Филянова [83]: Tg = 358 K, ц = 0.33-0.37, E = (28-35)-108 Па, fg = 0.025.

Процессу «делокализации атома» в стеклообразных органических полимерах соответствует предельное смещение небольшого участка основной цепи макромолекулы (предположительно группы атомов в соединительном звене) [6].

8.    Заключение

В настоящее время нет общепризнанного объяснения пластической деформации стеклообразных систем. Наибольшее распространение получило представление о том, что пластичность неупорядоченных твердых тел (неорганических стекол, аморфных органических полимеров, металлических стекол и т. д.) возникает и развивается через зарождение и накопление специфических структурных мелкомасштабных дефектов (локальных микросдвигов), получивших общее название «сдвиговых трансформаций». Сдвиговые трансформации являются носителями пластической деформации стекол. Концентрация носителей возрастает до стадии стационарного пластического течения, после чего выходит на постоянный стационарный уровень.

Модель делокализованных атомов можно рассматривать как один из вариантов такого общего подхода к природе пластичности стекол. Из этой модели вытекает линейная корреляция между температурой стеклования жидкости T g и пределом текучести — механическим напряжением a y , выше которого при 20 ° С наблюдается пластическая деформация стекол, что подтверждается экспериментальными данными. Это означает определенную взаимосвязь пластической деформации стекол и процесса стеклования. Можно предположить, что в окрестности температуры T g происходят такие же обратимые конфигурационные изменения структуры, которые наблюдаются при пластической (замороженной обратимой) деформации стекол. Размягчение стекла при нагревании в области T = T g и пластическая деформация стекла под действием механического напряжения при 20 ° С определяются одним и тем же молекулярным механизмом, а именно делокализацией атома — его предельным смещением из локального равновесного положения, которое связано с локальным конфигурационным изменением структуры.

Развито представление о том, что делокализация атома — предельное смещение активного атома — служит необходимым условием реализации элементарного акта вязкого течения стекол и их расплавов. Поэтому замораживание процесса делокализации атома («пускового механизма текучести») в области стеклования приводит к прекращению вязкого течения и к переходу расплава в стеклообразное состояние. Этот момент наступает тогда, когда энергия тепловых колебаний решетки, отнесенная к атому, становится равной или меньше энтальпии делокализации атома. Отсюда следует определенный критерий стеклования, который находится в согласии с экспериментальными данными.

Наиболее удобным и доступным способом исследования пластичности хрупких неорганических стекол служит наноиндентирование — вдавливание заостренных инденторов (например, алмазной пирамидки Виккерса от микротвердомера). Напряженное состояние под индентором локализуется в малом микрообъеме, линейные размеры которого меньше среднего расстояния между дефектами. Поэтому на результаты измерений не влияют дефекты, особенно поверхностные микротрещины. После микровдавливания индентора на стекле остается пластичный микроотпечаток. Из анализа напряженного состояния при микровдавливании алмазной пирамидки Виккерса следует, что под индентором возникает локальная деформация сдвига и что микротвердость по Виккерсу H V = F / S ( F — нагрузка на индентор, S — площадь микроотпечатка), определяемая как среднее нормальное напряжение, по величине совпадает с максимальным касательным напряжением τ m и служит характеристикой сопротивления материала сдвигу. Величина H V совпадает с пределом текучести σ y , выше которого происходит пластическая деформация стекла.