Эффект резкого увеличения коэффициента центробежного разделения газовых смесей в неравновесных условиях

системе отсчёта, движущейся вместе со струёй газа, у внешней стенки преимущественно накапливаются более тяжёлые молекулы HfCU, поэтому доля X этих молекул во внутреннем потоке будет меньше их доли 1 — X во внешнем потоке, что обеспечивает эффект разделения, который будем характеризовать коэффициентом разделения а = (1 — X )/X> 1. (1)

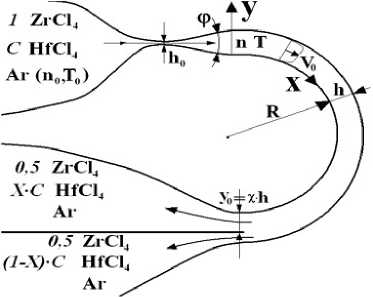
Рис. 1. Схема центробежного разделения ZrCl 4 и HfCl 4 в потоке газа-носителя (аргон), выходящем из щелевидного сопла в пространство, ограниченное концентрическими цилиндрическими поверхностями

• 2.    Количественный анализ процессов

В аргоновой струе, движущейся со скоростью V y , происходит диффузия молекул-примесей с коэффициентом диффузии D. Струя движется по дуге окружности радиусом R, поэтому в системе покоя струи на молекулу массы М действует центробежная сила F = MV 02 /R. Под действием силы F молекулы дрейфуют к внешней стенке со скоростями V = цҒ и V = цҒ, где ц = D/Т и ц = D/T — подвижности молекул. Здесь и далее величины, относящиеся к более лёгким молекулам ZrCl 4 , будут снабжаться верхней чертой. Постоянная Больцмана полагается равной единице, то есть температура Т измеряется в единицах энергии. В системе покоя введём координатную систему F, у ' , где оси F и у ' направлены соответственно вдоль и поперёк движения струи. Координаты лабораторной системы связаны с ними соотношениями х = х' + V y t, у = у ’ . Изменение концентраций примесей п и п описывается уравнениями диффузии

Эп (Жуу^^)  дау^^у^і) = дt +     Әу'         °

З у ^Ж'уу'^) = ^—D

дп^х^у^і) ду'

+ цҒп (х', у', t)

(уравнение для концентрации п (х, у, t) лёгких молекул записывается аналогично). Преобразуя уравнение к координатам лабораторной системы, получаем дп (х,у,і')       дп (x,y,t)    Эзу (х,у,€)

дt   ^{+ V} 0   дх   ⁺ —ду— = °’

З у ^{( х,} y ^{,t )} = ^—D

дп (х,у,1) ду'

+ цҒп (х,у,Ж .

с граничными условиями

^{n (0 ,} y⁾ = ^{1 ,}      n (0,y) = C,

—

—

З у ^(ж, ⁰⁾ = З у ^{( ж} , ^{К )} = ⁰,

Некоторые обозначения приведены на рис. 1,

З у (ж, 0) = З у (ж, К) = 0.

D =

4п а _г ст

/ гТ

V 2м

• —    коэффициент диффузии тяжёлых молекул ZrCl 4 и HfCl 4 в газе-носителе (см. [1], §12), вычисленный в приближении М , М ^ М а_; , с = 5 • 10 ¹⁵ см² — сечение рассеяния атомов аргона на тяжёлых молекулах. Таким образом, в принятом здесь приближении D = D, д = Д. Далее,

паг ~ n A; ^К

• —    плотность атомов аргона в струе, n A _; — плотность атомов аргона в резервуаре (здесь и далее величины с верхним индексом нуль относятся к резервуару, без индекса — к расширившейся струе),

Т = Т о ( К Г

• —    температура в струе, Тд — температура в резервуаре. Установка по разделению должна иметь высокую производительность. По этой причине давление насыщенных паров в резервуаре не должно быть слишком низким, то есть величина Т д не должна быть слишком малой. С другой стороны, по техническим причинам она не должна быть слишком высокой. Из этих соображений выберем для последующих количественных оценок Т д = 500 К. Во избежание образования кластеров температура Т в струе не должна быть слишком низкой. Далее полагаем Т = 100 K, что соответствует һ д /һ = 0,089. Тогда для скорости струи и коэффициента диффузии молекул ZrCl 4 и HfCl 4 в аргоне в струе, движущейся по кругу, получаем оценки:

  V) =

  
  

  5Т д Ма;

  
  

  1 - ( к Г

  
  

  = 6 • 10 4 см/с,

  
  

  3 • 10 ¹⁹ см ² n A _; [см ^{- 3} ] с

  
  

  .

  
  

Рассмотренное течение устойчиво по о тношению к развитию турбулентности при угле раствора диффузора (см. рис. 1) у < т^ЩЗ^ТЙ^К д ~ 0,3 радиана (см. [2], § 23). Здесь ж ~ 15 см ² /с — кинематическая вязкость расширившейся струи.

Наряду с координатой ж, отсчитываемой от сопла вдоль движения струи, будем пользоваться временем t = ж/Й д движения газа от сопла до точки ж.

Диффузия и дрейф молекул характеризуются временами t oiF = K 2 /D и t dr = h/V . Их отношения для тяжёлых и лёгких молекул равны, соответственно,

3 = ^t 5iF = ғҒҺ = Ғһ ^ 1880 ', t DR    D Т      R

• -  t _DIF    дҒ һ   Ғ Һ       Һ д

  • ³ = 1D7 = ТГ =    - ¹⁴⁰⁰R.

Начнём с рассмотрения поддающегося простому расчёту случая

3 » 1,     3 >  1.

В этом случае размеры диффузионного расплывания малы, поэтому профили концентраций выглядят примерно, как на рис. 2. Для определённости принято, что n (ж = 0, у) = 1/Һ, n (ж = 0,у) = C/h, поэтому r һ                            /*

/ Дуп(ж = 0,у) = 1,      / dyn (ж = 0,у)=С.

J о                               Jo

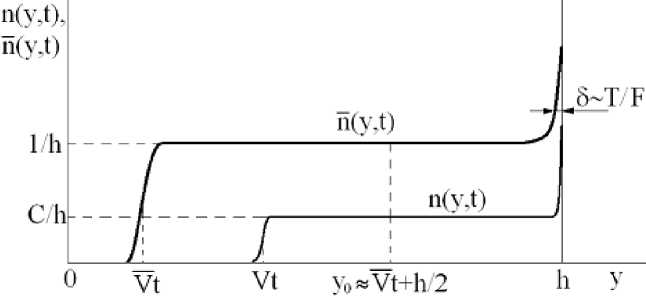
Рис. 2. Поперечные профили концентраций лёгких (п) и тяжёлых (п) молекул при t < t 1 = һ/ (2 V)

Молекулы не поглощаются стенками, поэтому, как следует из (2), эти соотношения выполняются для произвольного значения координаты ж:

N (ж, һ) = 1, N (ж, һ) = С,

где

Г У                                     ГУ

N (ж,у) =    dy' п ^-y^ ,     N (ж,у) = dy' п(ж,у') .

J о                                  Jo

В случае (3) диффузией нельзя пренебречь по сравнению с дрейфом только вблизи внешней стенки в слое толщиной 5Т/D ^ һ, где между этими двумя процессами приближённо устанавливается равновесие: j y та 0, j y та 0 (далее будем его называть 5-слоем). Отсюда и из (2) заключаем, что вблизи внешней стенки

—

F п (ж,у) та dL • Т • еХР

[                ],

/ х         ^{ғ       ғ (}у ^{- һ)}

^{П (ж,}у) ^та у н • Т • ^ехР ---- Т---- ,

где У L (ж) и у н (ж) — доли лёгких и тяжёлых молекул, находящихся в 5-слое.

2.1. Случай t <  t 1 = h) (2 V )

Согласно (4) площади под кривыми на рис. 2 с течением времени остаются постоянными. Как пояснялось выше, граничная поверхность у о = у о (ж) определена так, что в областях 0 < у < у о и у о < у < һ находятся по 50% молекул ZrCU. Положение границы у о и величина X , необходимая для нахождения коэффициента разделения (1), вычисляются из совместного решения уравнений:

^{N (ж,}уо) = 2 , X = N (у о ) /С.

При t < t 1 = һ/ (2V), как ясно из рис. 2, больше половины молекул ZrCU находятся в объёме, а в 5-слое их ещё меньше половины. Простой расчёт с использованием рис. 2 и уравнений (8), (9) даёт

у о та vt + һ/2,Х

1(1 -1)

һ                , . т + 1

^,Т =2 (V - V) >^{t 1 ,a ( t )} = Т — t.

Таким образом, с ростом t при t возрастает от значения a(0) = 1 до

<

t i = һ/ (2V) коэффициент разделения монотонно

a (t i )

т + ti _   1

т - ti = 22йЛ ¹ м

-

- =2,2. 1

2.2. Случай t 1 ₂ = h/V

Тяжёлые молекулы движутся к внешней стенке быстрее лёгких (V > V), поэтому они раньше лёгких оказываются в 5-слое: £2 < £3 = h/V. При £1 < £ < £2 = h/V граница у = уо расположена внутри 5-слоя, но в нём находятся ещё не все тяжёлые молекулы, а лишь часть их, равная ун ~ £/£2. (10)

Соответственно, доля лёгких молекул в 5-слое составляет

у - ~ £/£ 3 .

Из (5) и (6) получаем соотношение

Г           Г n / TXT'!

1 - TV ⁽ж, у) « у - • | 1 ^- exp [-------Л .

Отсюда и из (8) следует уравнение, определяющее положение граничной поверхности:

L       [^{ғ (}У о ^{- h)} ]1     ¹

^{y L} • р ^{- exp}[ -^- ) = ,,

то есть

[F (уо - h) 1           1, , exP ------- = 1 - —.

L - J

Соответствующие соотношения для тяжёлых молекул получаются аналогично:

Г                                             v I tv

^{1 -X} = ^{у н} • ( 1 ^{- exp} [ ^{ғ (у о} - ^{- К)} ]} = ^{у н} • ¹ - ( 1 - ^У - )

Отсюда и из (10), (11) следует, что во временном интервале £ 1 < £ < £ 2 коэффициент разделения (1) продолжает увеличиваться с ростом £. При £ = £ 2 все тяжёлые молекулы оказываются у внешней стенки (у н = 1), а часть лёгких молекул, равная 1 — у - = 1 — £ 2 /£ з = 1 — М/М = 0,27, ещё остаётся в объёме. В этот момент величина параметра X составляет

X = ⁽ 1 - Мf^M =0,203

V    2М)        ’

и коэффициент разделения достигает наибольшей величины a _max = а (£ 2 ) ~ 4.

2.3. Случай t ₂ < t < t ₃

В этом интервале у н = 1, поэтому из (13) и (1) имеем

м

X . ex^p [ ^Ғ-И ] = ( , - 2L) ^м ,

_ 1 - X

= X

где у - ~ £/£ 3 . С ростом £ лёгкие молекулы поступают из объёма в 5-слой. Из-за возникающего разбавления коэффициент разделения монотонно уменьшается от величины a _max до а (£ 3 ) = [1 - X (£ 3 )] /X (£ 3 ) « 1,59, где X (£ 3 ) = 2 ^{- М/м} ^ 0,386.

• 2.4. Случай t >  t ₃

В этом интервале оба типа молекул находятся в 5-слое, устанавливается равновесное состояние. Коэффициент разделения не меняется и равен стационарному значению а (£ 3 ) ~ 1,59.

Диффузионное расплывание границ понижает коэффициент разделения. Для учёта этого эффекта требуется выйти за рамки приближения (3) и решить уравнения (2) точно. Расчёт усложняется и поэтому вынесен в приложение. Результаты расчёта приведены на рис. 3 и 4. На рис. 4 используется безразмерная координата вдоль струи

^ _ 8 5 • 10 12     ^{ж [ см ]}

V q ^ ²     ,         П о [см ^{- 3} ] ^ 2 [см]

ж ’

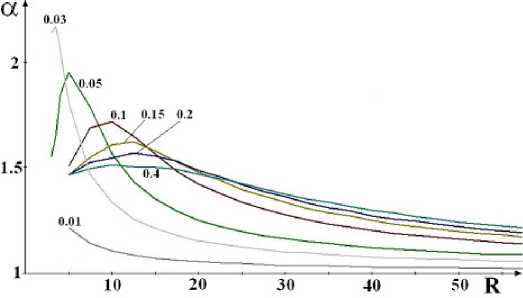
Рис. 3. Зависимость коэффициента разделения а от радиуса R концентрических цилиндрических поверхностей (см. рис. 1) при разных значениях безразмерной координаты ж ’ (указаны цифрами у кривых) для ширины щелевидного сопла һ о =0,05 см

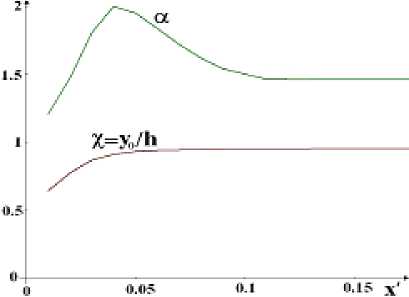
Рис. 4. Зависимость коэффициента разделения а и безразмерной координаты граничной поверхности х = У о /һ от безразмерной координаты вдоль струи ж ’ = жD /(V o h ² ) при R = 5 см для ширины щелевидного сопла һ о = 0,05 см

• 3. Выбор оптимального режима разделения. Заключение

Как показано выше, с ростом координаты вдоль струи ж коэффициент разделения а проходит через максимум. Физическая причина состоит в том, что более тяжёлые молекулы HfCl 4 раньше подходят к внешней стенке, чем ZrCU. При дальнейшем увеличении ж к стенке приближаются уже газ более лёгких молекул. Происходит «разбавление» в нём более тяжёлых, что ведёт к уменьшению коэффициента разделения.

Пользуясь рис. 3 и 4, несложно установить приемлемые для практики параметры установки. При выборе учитываем кажущееся естественным конструктивное ограничение на длину дуги: ж < 2^R.

Струя малой плотности п ^ _г ~ 2 • 10 ¹⁸ см ^{- 3} . При этом давление в камере-источнике струи составляет р ~ 0,3 атм, Һ д = 0,05 см, Һ = 0,5 см, п д_г ~ 10 ¹⁷ см ^{- 3} , ж ’ = 0,03, ж = 17 см, R = 6 см, Т ~ 100 K, Т д = 500 K, х ~ 0,8. Коэффициент разделения порядка а ~ 2. Чтобы не усложнять изложение, мы не будем здесь употреблять строгое выражение Дирака для производительности Q установки по разделению. Вместо этого определим её не строго, но наглядно, а именно, как число молей ZrCU, освобождённых от примесей HfCU за одну секунду на одном сантиметре длины вдоль щелевидного сопла: Q та Һ д Ү д п ^ /А ~ 10 ^{- 3} моль/см • с, где п ^ _г ~ 2 • 10 ¹⁷ см ^-3 — плотность молекул ZrCU в насыщенном паре в резервуаре, А = 6 • 10 ²³ моль ^{- 1} — число Авогадро. Это не строгое, но наглядное определение годится при представляющих практический интерес достаточно больших значениях коэффициента разделения а >  1,5.

Струя высокой плотности п ^ _г ~ 1 • 10 ¹⁹ см ^{- 3} . При этом давление в камере-источнике струи составляет р ~ 1,5 атм, Һ д = 0,05 см, Һ = 0,5 см, п д_г ~ 5 • 10 ¹⁷ см ^{- 3} , ж ’ = 0,03, ж = 80 см, R = 20 см, Т ~ 100 K, Т д = 500 K, х ~ 0,65. Коэффициент разделения порядка а ~ 1,2, то есть при высокой плотности струи он мал.

Из приведённого анализа следует, что центробежное разделение смеси газов намного выгоднее производить в неустановившемся режиме течения струи. Полученные оценки указывают на перспективность и возможность практического применения изложенного метода.

Приложение

Решение уравнений (2) для молекул каждого вида находится по методу Фурье и имеет вид

D

^{П (ж,}У) = ^2^Ь 8 ^Ф 8 ⁽7) exp ( ^{— Л} ^Һ 2 ^Ж ) ,

S = 1                  '             /

Ь д =

Р

exp Р — 1,

^p = ^ ^ф д ^{( y )} = exp (i⁷) ,^{ф ил} = ^exP (It) sin (^{k s} Һ ⁺ ^ ^s ) ,

,                         , ( 2ks X .       , 2 , р2 , ks = ^s,ps = arctg I — I , Л5 = ks + —, Ь= =

^2k s ^p [1 ^{— ( — 1) S} exp ^{( —р/ 2)]}

Отсюда, а также из (8), (9), получаем уравнения для нахождения

л 3 ^{/ 2}

величин х и X:

•

e ^3x e ³

-

-

∞

1+^x/ ² ^

S =1

k _s ^ 1 — e ^{3/ 2} ( — 1) ^s ] e ^л = ^ж ’

sin (k s X) ,

X =

e ^x el³

-

-

∞

- + 2pe ^{3x/ 2} ^

S =1

k _s [1

-

e ^{3/ 2} ( — 1) ^s l e ^л = ^ж ’

----------5--------------sin (ksx) •

(Л ₅ ) ^{2                   V}