Эффект стабилизации мартенсита в никелиде титана после предварительной деформации путём охлаждения под нагрузкой в неполном интервале превращения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

Сплавы с памятью формы (СПФ) широко применяются в промышленности и медицине благодаря их функционально-механическим свойствам. Способность восстанавливать исходную форму при обратном мартенситном превращении (переходе в высокотемпературную фазу – аустенит) после деформации в низкотемпературной фазе (мартенсит) делает СПФ эффективными для использования в термомеханических приводах и термодатчиках.

Характеристические температуры A_s и A_f , при которых начинается и заканчивается обратное мартенситное превращение, считаются константами материала. Однако исследования показали, что мартенситная фаза может сохраняться при нагреве до температур, превышающих A_s в недеформированном состоянии. Это явление известно как эффект стабилизации мартенсита (ЭСМ). В зависимости от области применения СПФ, ЭСМ может быть как полезным, так и нежелательным. Величина смещения температуры A_s зависит от степени предварительной деформации.

Эффект стабилизации мартенсита встречается в различных сплавах с памятью формы. Он наблюдался в сплавах на основе меди: Cu–Zn–Al [1; 2], Cu–Ni–Al [3], сплавах Гейслера [4; 5] и титана [6]. В никелиде титана эффект исследуется с 1991 г. В работе Лина (H.C. Lin) с соавторами [7] после холодной прокатки с уменьшением толщины в 40 % наблюдалось суще- ственное увеличение температур обратного превращения при первом нагреве. При повторном нагревании смещения температур не наблюдалось. В дальнейшем ЭСМ исследовался при различных методах предварительной деформации. В 1993 г. в исследовании Пиао (M. Piao) с соавторами [8] смещение температур при первом нагреве было вызвано с помощью деформирования образца растяжением в мартенситном состоянии. Позднее ЭСМ исследовался в работах Лию (Y. Liu) с соавторами [9–14] и других авторов [15; 16] при различных способах предварительной деформации: растяжение, сдвиг, вызванное напряжением превращение, охлаждение под нагрузкой. Эффект был обнаружен в моно- и поликристаллах сплава. В упомянутых исследованиях выдвигались различные гипотезы о причинах возникновения ЭСМ, но были впоследствии опровергнуты их же авторами или С.П. Беляевым с соавторами в работах [17–20].

В данной работе моделирование ЭСМ опирается на гипотезу, выдвинутую С.П. Беляевым с соавторами [20]. Согласно ей, основной причиной проявления ЭСМ является повреждение границ ориентационных доменов мартенсита, затрудняющее обратный переход и, следовательно, смещающее его температуры обратного превращения в большую сторону. Работа модели на основе данного предположения хорошо согласуется с экспериментальными данными [21; 22].

В исследовании [20] также было показано, что наблюдение ЭСМ можно предотвратить или минимизировать, если свести повреждение границ к минимуму.

С образцом из сплава Ti ₄₉ Ni ₅₁ был проведён эксперимент с охлаждением под нагрузкой в неполном интервале прямого превращения, при этом ЭСМ не наблюдался. Можно сделать предположение, что существует некое критическое значение доли прямого превращения, после которого начинается повреждение межмартенситных границ.

Основной текст1.    Микроструктурная модель СПФ

Моделирование     функционально-механических свойств – важный и удобный инструмент для изучения фазовых превращений и термомеханического поведения СПФ. Микроструктурная модель, описанная в работах [23–25], учитывает фазовую деформацию, пластическую аккомодацию мартенсита и эволюцию деформационных дефектов. Внутренними переменными модели являются объемные доли ориентационных вариантов мартенсита, полученных различно ориентированными бейновскими деформациями; микропластические деформации, связанные с этими вариантами; плотности ориентированных и рассеянных деформационных дефектов. Представительный объем состоит из зерен, которые содержат аустенит и варианты мартенсита. Макроскопическая деформация, описываемая тензором малых деформаций ε, рассчитывается по гипотезе Рейсса, как среднее значение деформаций зерен εgr. Для кристаллов деформация с хорошей точностью может быть разбита на сумму упругой εe , термической εT , фазовой εPh , микропластической εmp и пластической ε p составляющих:

^e= E f ^e gr ( o ) , ^e gr ^=e e ^+e T ^+e Ph ^+e mp ^+e p ,   (1)

где И i - ориентации кристаллографических осей, ft -объемные доли зерен с ориентацией о.) i , а сумма берется по всем ориентациям зерен (в дальнейшем аргумент o i опущен). Аналогично правило смеси применяется и к деформациям фаз внутри каждого зерна:

NN е g =(1 - Ф м )е A + - ЕФ n г Mn, Ф м = - ЕФ n,  (2)

N n = 1                  N n = 1

где ε ^A и ε ^Mn – деформации фаз аустенита и n -го варианта мартенсита, N – количество ориентационных вариантов деформации Бейна, реализующей изменение решетки, Ф _M – суммарная объемная доля мартенсита в зерне, Ф _n - нормированная (увеличенная в N раз) объемная доля n -го варианта мартенсита. Фазовая и микропласти-ческая деформации рассчитываются по формулам

NN еPh = _Уф Dn, гmp = _ VkepdevDn,      (3)

nn n=1                          ' n=1

где Dⁿ деформация Бейна. Вторая из формул (3) представляет собой упрощенный расчет микропластических деформаций, основанный на идее, что рост каждого варианта мартенсита инициирует пластические сдвиги, создающие деформацию, пропорциональную девиатору фазовой деформации. Переменные е Р задают величину микропластических деформаций, devDⁿ – девиатор тензора Dⁿ, к - материальная константа. Обобщенные силы, вызывающие изменение внутренних переменных Ф _n и е Р , рассчитываются как производные по этим переменным от потенциала Гиббса G. Для каждого зерна

G = ( 1 - Ф м ) G^a + N Е> n G Mn + G , (4)

где G^A и G^Mn – потенциалы аустенита и n -го варианта мартенсита без учета их взаимодействия, G^mix – потенциал смешивания – упругая энергия межфазных напряжений. В формуле (4) собственные потенциалы фаз равны

G a = G^a a - S^a a ( T - T _o) - c ° ⁽ T - T ⁰)— 00   0

^{2 T} 0               (5)

• ^{- е} Г ( ^T ) ° i ^- 2 D ia ° j ° ki ( ^a = ^A , ^Mn ) ,

где верхний индекс a = A обозначает аустенит, a = Mn -n-й вариант мартенсита; G0a и S0a – потенциал Гиббса и энтропия при напряжении °=0 и температуре T=T0, T0 -температура фазового равновесия (при которой G0A = GM ); еOTa (T) - деформации фаз при ° 0 ; c° и Dakl -удельные теплоемкости при °=0 и упругие податливо- m Ms + Af сти. Согласно работе [26]: T0~ 2—— (где Ms, Mf , As , Af – характеристические температуры превращения). Для оценки упругой энергии Gmix так же, как в работах [27; 28], вводится квадратичная форма, которая учитывает, что Gmix растет с ростом объёмных долей мартенсита Фn и уменьшается из-за ориентированных деформационных дефектов bn , рост которых обеспечивает пластическую аккомодацию мартенсита:

G =У Е N , n = 1 A mn ( Ф m - b m )( Ф n - b n ) ’       (6)

Матрица (Amn) описывает самодействие и взаимодействие вариантов мартенсита. В сплаве TiNi первичная самоаккомодация мартенсита достигается путем группировки вариантов в согласованные пары [29–31]. Для учета этого обстоятельства в работе [15] в матрицу (Amn) введены недиагональные отрицательные компо- ненты. Из формул (5), (6) находим, что сила, вызывающая рост n-го варианта мартенсита равна:

F(T , о , Ф)=- N — = q- TT - T ) + n (        )        ЭФ n T _o ^{(       0} )

1 о j : Dn "H^LAmn (Ф m — bm m=1

где q0 = To (SM - SA) - скрытая теплота превращения при температуре To : D” - компоненты тензора Dn.

Эксперименты по измерению температурных зависимостей объемной доли мартенсита и деформации показывают, что существует диссипативная сила F^fr , численно равная энергии диссипации, противодействующая движению границы раздела фаз и ответственная за гистерезис превращения, так что условие превращения имеет вид:

F n =± F f ,

где сила F n определена формулой (7), знак плюс соответствует прямому превращению, а знак минус - обратному. Для силы F f справедливо выражение: F f = q o ( M_s - T o ) / T o .

Законы изменения переменных b_n и г n , выводятся из условия течения:

|F p - F „ ^p| = F y , ( F np - F^ dF n >  O,         (9)

где F n ^p - обобщенная сила, сопряженная с b_n : d GN.

Fnp =- N^T = ^E Amn (Ф m - bm ) ’ F и F - силы, О bn    m= описывающие изотропное и кинематическое упрочнение. Условие течения (9) аналогично классическому условию течения для одноосного напряженного состояния: обобщенные силы Fnp , Fy и Fn играют соответ ственно роль напряжения, напряжения течения и внутреннего (собственного) напряжения. Микропластиче-ское течение генерирует деформационные дефекты, которые в данной модели разделяются на две группы: рассеянные f и ориентированные bn . Для них исполь зуются уравнения:

b n = k b ^f г m ^p -    г TH ( b n г m ^p ) 1 , f = f ^ m ^p |, (1O)

\ e                 )         m=1

где k_b , p * - материальные константы, H - функция Хевисайда. Предполагаем, что изотропное упрочнение создают рассеянные дефекты, а кинематическое - обратимые, то есть имеется связь дефектов f с силой F^y , а b n - с силой F n (так называемые замыкающие уравнения [32; 33]). В данной модели они выбраны в простейшей форме:

F y = a y f , F = a _p b n ,             (11)

где a_y и a _p - материальные константы. Из условий (8), (9) и формул (7), (1o), (11) следуют уравнения, позволяющие при заданных приращениях напряжения и температуры рассчитать приращения внутренних переменных Ф _n , г mp , b_n , f_n , а затем по формулам (1)-(3) рассчитать обратимую и необратимую макроскопическую деформацию.

• 2.    Расчёт повреждённости межмартенситных границ

Описание ЭСМ, так же, как в работах [21; 22], построено на идее расчета поврежденности межмартенситных границ и ее влияния на диссипативную силу Ffr. Наблюдения [2O] показывают, что границы повреждаются при росте мартенситных пластин на поздних стадиях МП, а также в процессе переориентации мартенсита при деформировании образцов в мартенситном состоянии. В данной модели характер поврежденности не конкретизируется, а переменная Z, задающая повре-жденность, изменяется от O до ^. Для описания ориентированности мартенсита введена переменная r = г / фм, где r = ^^^f NJФn - Фм| .

Отметим, что r = O для полностью хаотического мартенсита и r = 1 для полностью монодоменизиро-ванного мартенсита. При увеличении ориентированности мартенсита поврежденность границ растет, поэтому для расчета ее эволюции предложено уравнение:

d Z = k

( ^Ф M - ^Ф crit ) ^H ( ^Ф M - ^Ф crit ) ( 1 - Ф crit ) ( 1 + k ₃ Z ² )

drH ( dr ) ,

где k 1 , k 3 , Ф _crit - константы. Данное уравнение предполагает, что рост поврежденности границ происходит только, когда доля мартенсита Ф _M превышает критическое значение Ф _crit , а также то, что рост поврежденно-сти происходит с замедлением.

Для расчета изменения поврежденности границ в процессе прямого превращения предложено уравнение:

d ^ =            d Ф m H ( d Ф м ) ,

Фм (1 ' k3Z )

где переменная

Г - С ( ^Ф M - ^Ф crit ) ^H ( ^Ф M - ^Ф crit )~

^{Z 1 = k 2}          ( 1 - Ф -)

( k ₂ - константа) задает равновесное значение повре-жденности границ при заданной доле мартенсита Ф _M и его ориентированности r . Заметим, что Z 1

пропорционально r и линейно возрастает с ростом Ф _M , после того, как она превысит критическое значение Ф _crit . При обратном превращении поврежденность межмартенситных границ не меняется, то есть выполняется уравнение

d Z = 0,

Заметим, что эволюция поврежденности границ непосредственно не зависти от температуры и напряжения, н зависит только от изменения объемной доли и ориентированности мартенсита, которые, в свою очередь происходят под действием температуры и напряжения. Основная гипотеза о влиянии поврежденности мартенситных границ на мартенситное превращение состоит в том, что диссипативая сила сопротивления их движению F_M^fr_SE возрастает с ростом их поврежденности. В связи с этим для расчета силы F_M^fr_SE предложено уравнение:

fMMse = Ff(i + z k), где Ffr – сила сопротивления движению неповрежденных границ, k – константа материала, учитывающая нелинейность влияния повреждённости на диссипативную силу и, соответственно, на сдвиг характеристических температур обратного МП.

• 3.    Моделирование экспериментов по термоциклированию СПФ в неполном интервале прямого превращения

Экспериментальные данные из работы [20] указывают на то, что величина сдвига температур обратного МП зависит от доли прямого превращения при задании предварительной деформации путём охлаждения под постоянной нагрузкой. В связи с этим в данной работе выполнены расчеты, проверяющие способность модели описывать эту особенность ЭСМ. СПФ Ti ₅₀ Ni ₅₀ . и Ti ₄₉ Ni ₅₁ охлаждали под постоянной нагрузкой 100, 200 или 300 МПа. Для каждого напряжения было проведено 10 численных экспериментов с долей прямого превращения K от 10 до 100 %. Эту долю рассчитывали, как *

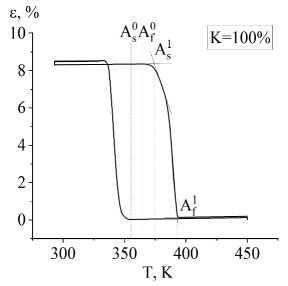
—охл • 100 %, где еохл - деформация после охлаждения ^охл под нагрузкой в неполном интервале превращения, еохл -в полном. Температуры превращений определялись методом касательных. На рис. 1 показаны расчеты для K = 100 % и K = 75 %.

При моделировании использовались следующие значения констант.

Для сплава Ti ₅₀ Ni ₅₀ : характеристические температуры:     M s = 330 К ,     M_f = 337 К ,     A s = 355 К ,

A f = 362 К , скрытая теплота превращения:

q 0 = - 220 МДж/м³; константы для описания ЭСМ: к 1 = 5,6, к ₂ = 4,0, к 3 = 0,75, Ф _crit = 0,3, к = 1,8.

Для сплава Ti49 Ni51 : характеристические температу ры: М^ = 253 К, Mf = 240 К, A = 266 К , Af = 276 К, s    fs   f скрытая теплота превращения: q 0 =-150 МДж/м3; константы для описания ЭСМ: k1 = 2, 2, k2 = 4, 0, k3 = 0, 3, Ф c„t = 0,3, к = 1,8.

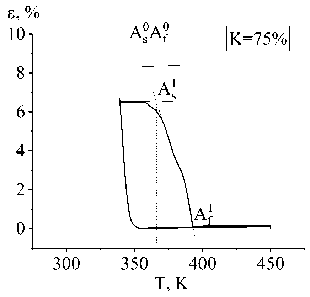
b

Рис . 1. Расчетные зависимости деформации от температуры в сплаве Ti 50 Ni 50 при охлаждении под постоянной нагрузкой 100 МПа до доли прямого превращения K=100 % ( а ) и K=75 % ( b )

Fig. 1. Calculated temperature dependences of deformation for Ti 50 Ni 50 alloy when cooled under a constant load of 100 MPa to a direct conversion fraction of K=100 % ( a ) and K=75 % ( b )

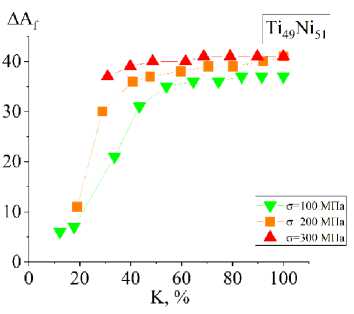
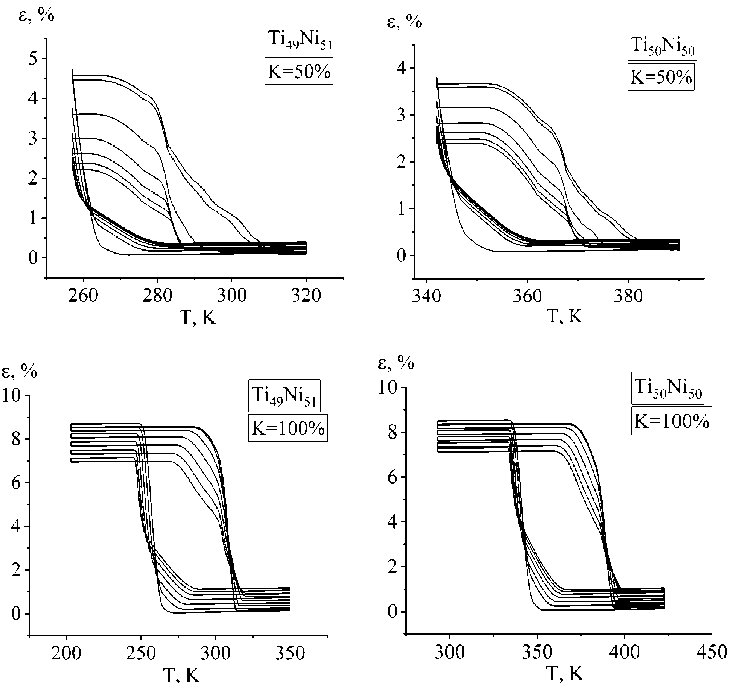
Температуры фазовых превращений были взяты из работы [17], а остальные константы были определены на основе экспериментальных данных, приведённых в этом же исследовании. На рис. 2 и 3 представлены результаты численных экспериментов для сплавов Ti ₅₀ Ni ₅₀ и Ti ₄₉ Ni ₅₁ соответственно.

Кроме расчетов однократного нагрева после задания предварительной деформации, было проведено моделирование 50 циклов по режиму: [нагрузка до 100 МПа → охлаждение до K=50 %; 75 % или 100 % → разгрузка → нагрев до аустенитного состояния] в сплавах Ti ₅₀ Ni ₅₀ и Ti ₄₉ Ni ₅₁ . Зависимости сдвига температур начала и конца обратного МП от номера цикла для рассматриваемых сплавов показаны на рис. 4 и 5, а зависимости деформации от температуры для некоторых термоциклов – на рис. 6.

a

b

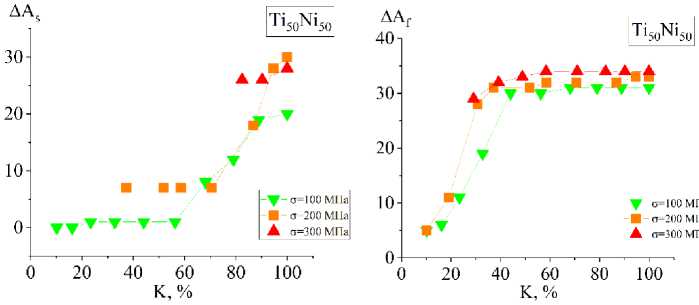
Рис. 2. Зависимости сдвига температур начала ( а ) и конца ( b ) обратного мартенситного превращения от доли прямого превращения K при охлаждении под постоянной нагрузкой 100, 200 и 300 МПа в сплаве Ti 50 Ni 50

a

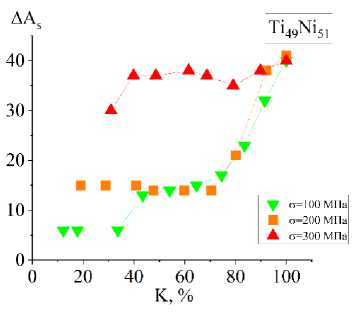
Рис. 3. Зависимости сдвига температур начала ( а ) и конца ( b ) обратного мартенситного превращения от доли прямого превращения K при охлаждении под постоянной нагрузкой 100, 200 и 300 МПа в сплаве Ti 49 Ni 51

Fig. 2. Dependences of the temperature shift of the beginning ( a ) and end ( b ) of the reverse martensitic transformation on the fraction of the direct transformation K when cooled under a constant load of 100, 200 and 300 MPa in Ti 50 Ni 50 alloy

b

Fig. 3. Dependences of the temperature shift of the beginning ( a ) and end ( b ) of the reverse martensitic transformation on the fraction of the direct transformation K when cooled under a constant load of 100, 200 and 300 MPa in alloy Ti 49 Ni 51

■ K-50%

a

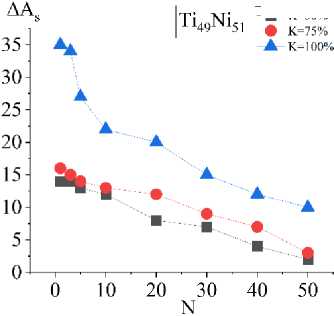
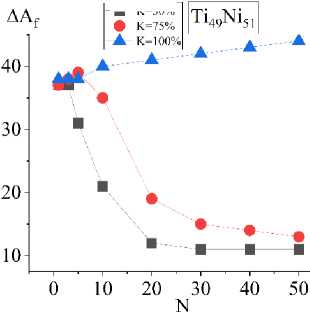
Рис. 4. Зависимости сдвига температур начала ( а ) и конца ( b ) обратного мартенситного превращения от номера цикла N при охлаждении под постоянной нагрузкой 100 МПа до достижения доли прямого превращения 50, 75 и 100 % в сплаве Ti 49 Ni 51

■ K-50%

b

Fig. 4. Dependences of the temperature shift of the beginning ( a ) and end ( b ) of the reverse martensitic transformation on the cycle number N when cooled under a constant load of 100 MPa until the proportion of direct transformation of 50, 75 and 100 % in alloy Ti 49 Ni 51 is reached

■ К=50%

• К=75%

K=50%

К=75%

К= 11Ю%

b

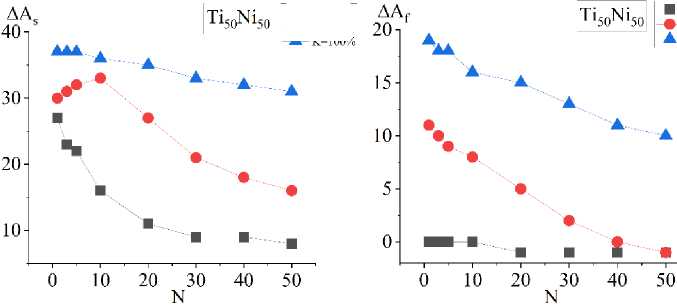
a

Рис. 5. Зависимости сдвига температур начала ( а ) и конца ( b ) обратного мартенситного превращения от номера цикла N при охлаждении под постоянной нагрузкой 100 МПа до достижения доли прямого превращения 50, 75 и 100 % в сплаве Ti 50 Ni 50

Fig. 5. Dependences of the temperature shift of the beginning ( a ) and end ( b ) for reverse martensitic transformation on the cycle number N when cooled under a constant load of 100 MPa until the proportion of direct transformation of 50, 75 and 100 % in the Ti 50 Ni 50 alloy is reached

b

a

Рис. 6. Зависимости деформации от температуры в сплавах Ti 49 Ni 51 ( а ) и Ti 50 Ni 50 ( b ) в 1, 2, 10, 20, 30, 40 и 50-м термоциклах, включающих охлаждение под постоянной нагрузкой 100 МПа до достижения доли прямого превращения K=50 % и 100 % и нагрев в свободном состоянии

Fig. 6. Temperature dependence of deformation in alloys Ti 49 Ni 51 ( а ) and Ti 50 Ni 50 ( b ) in 1, 2, 10, 20, 30, 40 and 50 thermal cycles, including cooling under a constant load of 100 MPa until the direct conversion fraction K = 50 % and 100 % is reached and heating in a free state

• 4.    Обсуждение

Можно заметить, что во всех режимах нагружения с ростом доли прямого превращения K смещение температур обратного превращения увеличивается. Качественно это согласуется с экспериментальными данными, представленными в работе [20]. Модель предсказывает ослабление ЭСМ с циклами. За 50 циклов в неполном интервале превращения температуры обратного превращения смещаются до первоначальных и ниже. В циклах с полным интервалом превращения в это время также наблюдается уменьшение температур обратного превращения, однако оно менее значительное и не достигает исходных значений.

Заключение

Предложенные в предыдущих работах эволюционные уравнения для подсчёта степени повреждённости