Эффективная модификация уравнения Клейна – Гордона для частицы в потенциальном поле

Волновое релятивистски инвариантное уравнение гиперболического типа для частицы с не равной нулю массой покоя m ≠ 0 , позже названное уравнением Клейна – Гордона (кратко – уравнение КГ), впервые было сформулировано в 1926 г. Э. Шредингером, который, однако, не стал его публиковать, поскольку считал, что «его решение неправильно описывает наблюдаемый энергетический спектр атома водорода». Вскоре это же уравнение сформулировали независимо от Шредингера и друг от друга О. Клейн, В.А. Фок, В. Гордон и другие [1]. Позже было установлено, что уравнение КГ описывает так называемое скалярное физическое поле, создаваемое частицами с не равной нулю массой покоя и нулевым спином.

В частности, если такая частица находится во внешнем постоянном потенциальном поле V (x, y, z) (например, электростатическом), то соответствующее уравнение КГ имеет вид [2–5]:

v 2,1 L д V(x, У, z) 1 v +I iI c2 l д t h )

Г Л 2

( mc 1

Т ( x , y , z , t ) = I —I T ( x , y , z , t ),      (1)

l h )

где i - мнимая единица, h - постоянная Планка, с - скорость света, Т(x, y, z, t) - волновая функция частицы. Это уравнение получается из принятого в релятивистской физике выражения для функции Гамильтона частицы в таком поле [3]

H ⁽ P x , P y , P z , x , y , ^z ) = V⁽ mc ^{2 ) 2 + (} P x ⁺ р У ⁺ P 2 ) ^{c 2 +} V ⁽ x ’ y ’ ^z )     ⁽²⁾

путем ставших стандартными замен «квантования» [2–4]

н^ifo—, Px ^— ih—, Py ^— ifo—, pz ^-ih—, ∂t             ∂x             ∂y             ∂z посредством которых «корпускулярное» описание движения частиц заменяется «волновым» описанием эволюции поля, связанного с этими частицами.

Впоследствии было установлено, что погрешность в количественном описании основных особенностей спектра атома водорода посредством уравнения КГ относительно невелика и обусловлена, в основном, тем, что спин электрона не равен нулю и, следовательно, отсутствием учета спин-орбитального взаимодействия. Однако после того, как Шредингером были сформулированы два его знаменитых нерелятивистских уравнения, а физическим сообществом была принята «копенгагенская» интерпретация волновой функции, согласно которой квадрату ее модуля в ее координатном представлении придается смысл плотности вероятности обнаружения частицы с определенной энергией в некоторой точке пространства, оказалось, что решения уравнения КГ обладают более существенными недостатками. Дело в том, что это уравнение представляет собой дифференциальное уравнение второго порядка по времени, обобщающее хорошо известное аналогичное «обычное» волновое уравнение (описывающее, например, распространение электромагнитных волн) на поля частиц с ненулевой массой покоя. Поэтому решения Т(Г, t) этого уравнения зависят от значения в начальный момент времени не только самой волновой функции Ψ , но и ее производной по времени дТ / дt. Оказывается, что из-за этого квадрат модуля волновой функции ТТ * при t > 0 может, в принципе, принимать не только положительные, но и отрицательные значения, и поэтому данная величина не может иметь смысл плотности вероятности, являющейся, по определению, строго неотрицательной величиной. По этой причине квадрат модуля функции, являющейся решением уравнения КГ, нередко стали интерпретировать как плотность электрического заряда частицы [2,3]. Однако такая интерпретация допустима только после введения вторичного квантования скалярного поля, описываемого уравнением КГ, поскольку знак электрического заряда отдельной частицы не может быть разным в разных точках поля.

Еще одна неприятность, связанная с уравнение КГ (которую автор данной работы считает главной), заключается в том, что точные решения этого уравнения для водородоподобных атомов, соответствующие так называемым s - состояниям электрона, не обращаются в ноль в центре атома, более того, они в этой точке сингулярны [2,5]. С физической точки зрения это означает, что, согласно данной теории, атомы должны быть в принципе нестабильны , поскольку электрон имеет ненулевую (и довольно большую) вероятность находиться в ядре, а значит, сначала упасть на него; и чем больше заряд ядра, тем эта вероятность больше.

Такие разочаровывающие результаты значительно уменьшили интерес физиков к уравнению КГ. Тем не менее, некоторые авторы, стремясь избавиться от этих недостатков, предприняли попытки модификации уравнения КГ (1), о чем будет кратко сказано ниже. К сожалению, часть этих модификаций базируется на весьма произвольных допущениях, которые нельзя признать достаточно обоснованными. Другие исходят из некоторых модификаций гамильтониана, принципиально не меняющих его структуру. Есть и более сложные варианты.

В данной работе модификация уравнения КГ основывается на модификации функций Лагранжа и Гамильтона, предложенной и качественно обоснованной автором в работе [6]. Достоинством данной модификации, позволившем автору назвать ее «эффективной», является то, что посредством нее удалось устранить указанные выше недостатки решений уравнения КГ.

При этом, говоря о функции Т ( x , y , z , t ), автор будет называть ее не «волновой», а «полевой» функцией, считая этот термин более соответствующим физическому смыслу данной величины.

Несколько слов о стандартном уравнении КГ (1) для частицы в потенциальном поле и некоторых его модификациях

Вернемся к стандартному уравнению КГ вида (1). Раскрыв в нем квадрат разности операторов, стоящих слева, и перегруппировав члены, это уравнение нетрудно привести к виду:

„2    1 д ²       , V дТ (mc^

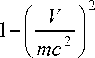
Ψ

V ²           Т = 2 i + I|

(       С ² д t ² J         hc ² д t l h J

(здесь для краткости записи аргументы функций V ( x , y , z ) и Т ( x , y , z , t ) опущены).

Отсюда следует, что если внешнее поле не равно нулю, то уравнение КГ (4) оказывается комплексным (в первом члене справа стоит мнимая единица) и содержащим не только вторую, но и первую производную по времени от искомой функции. Кроме того, потенциальная энергия V частицы входит в уравнение (4) не только линейно (и при этом в любопытный член с i дТ / д t ), но и квадратичным образом.

Напомним, как осуществляется переход от уравнения КГ (4) к нерелятивистскому нестационарному уравнению Шредингера и отметим, при каких ограничениях на потенциальную энергию частицы V ( x , y , z ) и полевую функцию Т ( x , y , z , t ) такой переход возможен [2,3]. Итак, следуя [2,3], ищем решение уравнения (4) в виде

Т ( x , y , z , t ) = y ( x , y , z , t ) exp

. | mc ² |

— i I           1 1

l h J

Тогда

V ² T= exp

. | mc ² |

— i ¹           1 1

l h J

∂Ψ

---= exp

∂ t

. | mc ² |

— i ¹           1 1

l h J

∂ψ ∂ t

. | mc2 | i |-------I w l h J

, (6)

V2y д2Т ltr"exp

- i

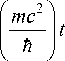
д ² ш „. | mc ² | дш | mc ²

----z--2 i -------------- д t2 I hl д t I h

Подставив равенства (5)–(7) в уравнение (4), после простых преобразований приходим к уравнению

- m

h ) 2

mc

3 2 v    L

—5-+ i hl 1 - d t ²       I

V mc ²

dy     h ² „2     (   V )

V V 1V11 -   2 Iy, dt    2m        ^ mc )

являющемуся точным следствием исходного уравнении КГ (4).

Нестационарное нерелятивистское уравнение Шредингера (уже параболического типа) для частицы в потенциальном поле [2–4]

dV i h — -d t

^^^^^^e

h ²

— ^V + V ( x , y , z ) у 2 m

получается из уравнения (8) при условиях

1 c ²

d ² у d t ²

<<|v 2 v|

I V I <<  mc ² .

Нетрудно показать, что первое из этих условий эквивалентно неравенству p ² / 2 m <<  mc ² и означает малость кинетической энергии частицы по сравнению с ее энергией покоя. Второе же условие означает малость модуля потенциальной энергии частицы по сравнению с той же энергией покоя.

Заметим, что, поскольку в уравнении Шредингера (9) отсутствует вторая производная по одной из независимых переменных, то это уравнение относится уже не к гиперболическому (как уравнение КГ (1)), а к параболическому типу. Это, на первый взгляд, физически несущественное изменение типа уравнения приводит к принципиальной разнице в характере некоторых решений исходного (1) и «укороченного» (9) уравнений. В частности, в то время как уравнение (9) не имеет решений в виде стабильных, локализованных в пространстве и не расплывающихся с течением времени волновых пакетов, соответствующих свободным частицам, гиперболические уравнения вида (1) такие решения имеют . Поэтому, с точки зрения автора, в методологии и интерпретации квантовой теории приоритетным следует считать не уравнение Шредингера, а уравнение КГ, но, конечно, при условии его модификации, устраняющей упомянутые выше недостатки решений этого уравнения.

Снова вернемся к исходному уравнению КГ (1) и попытаемся свести его к уравнению Шредингера (9) другим способом, считая выполненным лишь первое из условий (10). Для этого предположим, что наличие внешнего потенциального поля приводит к изменению лишь правой части уравнения (1), описывающей распределенные источники собственного поля частицы, оставляя неизменной чисто «волновую» левую часть этого уравнения. Предполагая также, что линейная зависимость этих источников от величины собственного поля частицы Т(x, y, z, t)

сохраняется, мы приходим к выводу, что единственная возможность модификации уравнения (1) состоит в замене постоянного множителя ( mc I й) ² в его правой части на некоторую, пока неизвестную функцию координат, вид которой определяется характером зависимости V = V ( x , y , z ).

В соответствии с этими соображениями перепишем уравнение (1) в виде

(_.   1 д ² )

I V ²   - I Т ( x , y , z , t ) = ^ ( x , y , z ) T ( x , y , z , t ),              (11)

I        c2 д t2 J где £(x, y, z) - функция-параметр, связь которой с потенциальной энергии V(x, y, z) частицы необходимо найти.

Будем искать решение уравнения (1) в виде:

Y ( x , y , z , t ) = у ( x , У , z , t )exp l - i-t- I .                      (12)

( T о J

Подставив это выражение в уравнение (11), после простых преобразований мы приходим к уравнению для функции у ( x , y , z , t ):

V ² у —

1 д ² у

+ c 2 д t2

2 i ду c ² T ₀ д t

5 ( ^x , y , ^z ) ^—

1____

( cT о ) ²

ψ .

Пренебрегая, в соответствии с первым из неравенств (10), членом с второй производной по времени д ² у I д t ² и умножая полученное

равенство на й ² I2 m , получаем уравнение

. й ² ду      й ² „2 й ²           .       1

i~ = ^{—V у +}     ^ ^{( x} , у , ^z )

c ² T 0 m д t     2 m       2 m [            ( cT ₀) ²

ψ ,

имеющее структуру уравнения Шредингера.

Потребуем, чтобы коэффициент при производной ду I д t

совпадал с соответствующим коэффициентом i й в уравнении

Шредингера. Отсюда находим, что Т _о = й I mc ². В результате

уравнение (14) принимает вид

., ду     й ²          й ²

i й   =—   V 2 у + д t    2 m      2 m

^ ^{( x} , У , ^z )

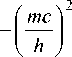
ψ .

Это уравнение совпадает с уравнением Шредингера (9), если

й ²

2 m

^ ^{( x} , У , ^z )

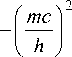
= V ⁽ x , y , z ),

т.е. если

( Л 2

² Г + ² V ^{( x} , y , z )

L mc

> 0.    (17)

( mc 1 2 m            ( mc

S ( x , y , z ) = | —I ⁺ —TV ⁽ x , y , z ) = 1 — l Й J Й ²             l Й

Подставив (8) в (1), мы приходим к модификации уравнения КГ

2r

„2 1 d ]„,,             ( mc I , 2 V ( x , y , z )

v —Г7Т к (x,y, z,t) = ItI 1 +------2  *(x,y,z,t), c2 dt2 )               l Й J L      mc2 J которую мы назовем модификацией В.М. Галицкого, в книге [5] которого (и его соавторов) приведен стационарный вариант данного уравнения. Его принципиальными отличиями от исходного уравнения КГ (4) являются вещественность, отсутствие производной Э* / dt и появление эффективной потенциальной энергии 2 V вместо ожидаемой величины V .

Заметим, что чаще всего рассматриваются стационарные решения уравнения КГ. Соответствующее стационарное уравнение КГ для не зависящей от времени функции у(x, y, z), которое получается из (4) подстановкой * = ^exp (iEt / Й), где E — энергия частицы, имеет вид [2–4]:

[ ( й c ) ² V ² + ( E - V ) ² - ( mc ² ) 2 ] ^( x , y , z ) = 0.                  (19)

Существенно, что решения именно этого уравнения для атома водорода, находящегося в любом из s -состояний (включая основное состояние), сингулярны в центре атома, свидетельствуя о невозмож- ности длительного существования атомов, что явно противоречит опыту.

Модифицированное уравнение КГ вида (18) приводит к следующему стационарному уравнению для функции у(x, y, z):

[ ( й c ) ² V ² + E ² - 2 Vmc ² - ( mc ² ) 2 ] ^( x , y , z ) = 0.                (20)

В ряде работ (см., например, [7–10]) приводится и решается модифицированное стационарное уравнение КГ такого вида:

[ ( й c ) ² V ² + E ² - ( v + mc ² ) 2 ] ^( x , y , z ) = 0.                  (21)

А.Э. Дангян в основу нового решения задачи об энергетическом спектре водородоподобных атомов [11] положил уравнение

^V

2 ( mc 1 ²

^^^^^^в

Й

2 Л2

mc 1

E - V J

^^^^^^в

1 Г V( x , y , z ) = 0.

К сожалению, ни эти, ни другие известные автору варианты модификации уравнения КГ не привели к устранению проблем, связанных с данным уравнением. Поэтому представляются заслуживающими внимания поиски такой модификации этого уравнения, которая все же избежала бы упомянутых выше проблем.

Предлагаемая модификация уравнения КГ длячастицы в потенциальном поле

Вернемся к уравнению (18). Легко убедиться в том, что ему соответствует функция Гамильтона

H I ⁽ P x , P y , P z , x , У , ^z ) = mcc

1 + ² V ⁽ x , У , Z ) mc ²

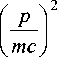
Обратим внимание на двучлен, стоящий в квадратных скобках в правых частях уравнения (18) и функции (23). Очевидно, этот двучлен можно рассматривать как два первых слагаемых в разложении квадрата бинома:

1+™ mc _

1 + ² V ⁽ x , y , ^z ) mc ²

+

V ( x , У , z )

mc ²

последний член которого (разложения) (V/mc2)2 отброшен из-за его малости, что допустимо при V(x, y, z)| << mc2. Данное обстоятельство наводит на мысль, что в качестве функции Гамильтона в рассматриваемом случае, возможно, физически более правильно использовать не функцию (23), а функцию, отличающуюся от нее заменой выражения, заключенного в квадратные скобки, на квадрат суммы:

1 + 2 V ⁽ x , у , ^z ) mc ²

Г                4-12

^ 1 + 1ХЫу!

mc

.

Эта мысль подкрепляется еще и тем, что предлагаемая замена восстанавливает симметрию подкоренного выражения в формуле для функции Гамильтона, которое теперь будет представлять собой сумму квадратов двух величин (заметим, что именно такая симметрия имеет место в случае свободной частицы (т.е. при V = 0), в то время как в формуле (23) эта симметрия отсутствует). Конечно, стремление к восстановлению симметрии в данном случае можно считать не очень убедительным доводом, но не стоит забывать, что соображения симметрии уже сыграли и продолжают играть одну из главных ролей в современной физике, поспособствовав ее многим важным достижениям и открытиям.

Таким образом, учитывая эти соображения, мы постулируем следующий вид функции Гамильтона массивной частицы во внешнем скалярном поле V ( x, у, z ):

H II⁽ P x , P y , P z , ^x , У , ^z ) = V [ mc ^{2 + V (} x ’ У ’ ^{z )]2 + (} Pc ⁾² . ⁽²⁶⁾

Тогда соответствующая модификация уравнения Клейна – Гордона, которая формально получается из (26) путем подстановок (3), принимает вид:

2                     Л.„.,л\2Г-\~1

• 1    д                   । mc I       V ( x , y , z )

• V-.      IT(x’y’z’t) = ItI 1 + me2     T(x’y’z’t).

X c t                 X

Подчеркнем, что функция Гамильтона (26) в точности совпадает с выражением для этой функции, предложенным автором в работе [6] (см. формулу (15) этой работы) и качественно обоснованным исходя из совершенно иных соображений. Такое совпадение, на взгляд автора,    свидетельствует о непротиворечивости и физической корректности данной функции.

Отметим, что модифицированное уравнение (27), как и стандартное уравнение КГ (1), является релятивистски инвариантным. Но при этом оно, в отличие от (1) или (4), является вещественным и не содержит первую производную по времени дТ / д t , что автор считает несомненными достоинствами данного уравнения.

Функция Лагранжа бесспиновой частицыи лагранжиан скалярного поля

Найдем функцию Лагранжа L II ( и , Г) , соответствующую функции Гамильтона H II (26). Согласно [12,13], эти две функции связаны между собой соотношением:

Hи + Lи = (p -и), где взаимосвязь импульса p и скорости и частицы определяется каноническим уравнением Гамильтона дHii

--- = и, дp’ а (p - и) обозначает скалярное произведение векторов p и и.

Дифференцируя функцию (26) по p, находим:

д Hn              c1- -

-I- =                            p = и , дp    Vtmc2 + V (r, t )]2 + (pc )2

откуда

I 1 + ^ ( r ? I

^— —. ^— X mc J —. p ( u , r, t) = .        =• m и .

V1 - ( u / c )²

Тогда

( Р - и) =

(1 + V ( rt ) )

^l mc    m и ² ,

71 - (и/ c ) ²

p ) ² = ( 1 + V ⁽ г,t ) ) mc ) l mc ² )

( u / c ) ²

1 - ( u / c ) ²

Подставив выражение (26) в формулу (28) и учтя равенства (32), мы приходим к искомому выражению для функции Лагранжа L II ( u , г) :

L _n( u , r) = - mc⁷

1 u ² L V (r,t ) )

1 —Г I 1 +---Т I, c l mc )

которое в точности совпадает с выражением (87) работы автора [6] и выражением (32) его работы [14], полученным еще одним независимым способом.

В отсутствие внешнего поля эта функция сводится к известному выражению [15,16] для свободной релятивистской частицы, а при наличии такого поля она отличается от стандартных выражений [15,16] тем, что «лоренцевский» (релятивистский) фактор 71 -(u/c)2 относится не только к энергии покоя частицы mc2, а к всему энергетическому комплексу mc2 + V(r, t).

В рассматриваемом нами случае бесспиновой частицы, находящейся в скалярном внешнем поле, соответствующий . ( AH' AH' A f AH' . A лагранжиан l T        r t = L T xi , из которого вытекает

L =

1 дТ( x ) дТ( x ) ( mc

2 *

-

д x k     д x k    I й

7 г-                     .

² л V ( r , t )

1 ■ mc

² , I ■ T² ( x )!•,

к где xk и x – ковариантные и контравариантные компоненты четырехмерного вектора x = (r, ict). Тогда уравнение (27) является конкретной (соответствующей нашему случаю) уравнения Лагранжа – Эйлера [17,18]:

dL__д dL = 0 dT(x) дXk д ( dT(x) | l дxk )

Отметим, что, согласно выражению (34), модели взаимодействие бесспиновой частицы со описывается не только линейным по V ( r, t )

формой общего

в предложенной скалярным полем членом, как в

стандартной классической теории поля [17], а суммой линейного и квадратичного по V(F, t) членов, причем вклад последнего члена пренебрежимо мал лишь в случае слабого поля, когда V(r, t) | << mc2.

Решение проблемы смены знака в распределенииплотности заряда частицы в сильном поле

Далее мы будем предполагать, что модифицированное уравнение КГ (27) справедливо не только в случае скалярного поля, но и при наличии любого внешнего потенциального поля V(x, y, z), в том числе электростатического (в частности, кулоновского) поля. Следуя стандартной методике (см., например, [2,3]), найдем выражения для величин, которые в квантовой механике трактуются как плотность заряда частицы р(F, t) и плотность электрического тока j (r, t), обусловленного движением данной частицы. Для этого уравнение (27) умножим слева на функцию V *(r, t) (звездочка обозначает комплексное сопряжение функции), уравнение, комплексно сопряженное уравнению (27), слева умножим на функцию V(г, t), и из первого полученного равенства вычтем второе. Учитывая, что

„а2        а2 * а ( * а       а Д v — v-v—v =—I v — v-v—v I, д t2         д t2 д t ( д t        д tJ

V *V2 V-VV2 V * = div (v *VV-VVV *), и вводя обозначения

p( F, t) =     f V* — V-V — V*),

2mc2 ( дtд j (F, t) = -—(V*VV-VVV*)

• 2    m

(где p ( r, t ) и j ( ^F , t ) — вещественные функции), мы получаем обычное уравнение непрерывности [2,3]:

^P^rlt) + div F (F, t) = 0, д t причем равенства (37)–(39) остаются справедливыми и при наличии внешнего потенциального поля V(F).

Этот результат принципиально отличается от того, который имеет место в случае стандартного уравнения КГ (1) при наличии такого поля. В частности, в случае пионного атома, т.е. отрицательно заряженного п- -мезона, находящегося в кулоновском поле протона, это уравнение приводит к следующему выражению для плотности заряда [2]:

p‘ ( r, t ) = i^- ( У * |у-т|у * I + -^a^L у * у ,         (40)

2mc2 ( дt       dt J mcr где a =-------= 7,297 -10 -3

4 ne ₀й c

<< 1 — постоянная тонкой структуры.

В стационарных состояниях, когда У (Г t ) = exp I - — Ett I у ( r), l й n Jn^

плотность заряда, как следует из формулы (40), определяется выражением

? /rx         e й I               e 1 | * _zr.      _zr

P n ⁽ r ) =-- yl ^E n -        ^-- I V n ⁽ r ) V n ^{( r} ) .               ⁽⁴¹⁾

mc ² l      4 ne о й r J

Отсюда следует, что при

. * r < r

= — |й Е_п ¹ функция p n ( r) меняет свой

4 ne.

• о

знак на противоположный. Это, безусловно, существенный недостаток стандартной теории, который не позволяет сохранить в ней одночастичную интерпретацию функции p‘ ( r) при r <  r * , т.е., фактически, в области сильного поля [2]. По этому поводу обычно замечают, что «физический смысл изменения знака ρ′ в сильном поле может быть понят только на основе теории, описывающей поведение систем с переменным числом частиц, учитывающей процессы рождения и уничтожения частиц обоих знаков зарядов» (см., например, [2]).

В то же время формула (37), полученная на основе модифицированного уравнения КГ, дает такое распределение плотности электрического заряда частицы в стационарных состояниях атома,

P n ^{( r )} = ^- -e^ E n I V П ^{( r )} V n ^{( r )} , mc

которое сохраняет знак заряда во всем пространстве.

Полученный вывод о том, что модифицированное уравнение КГ в стационарных состояниях приводит к выражению (42) для плотности электрического заряда, исключающему возникновение трудностей со сменой знака заряда в сильном поле, можно рассматривать как существенный довод в пользу именно этого уравнения .

Стационарные решения модифицированного уравнения КГ

Будем искать стационарные решения модифицированного уравнения КГ (27) в виде:

* n ⁽ r , t ) = V n ⁽ r ) exp

i ,       2

-- ⁽ mc + E n ) t П

Подставив выражение (43) в уравнение (27) и вычислив вторую производную по времени от (43), после несложных преобразований приходим к дифференциальному уравнению для функции у n ( r) :

<- — V² + V ( Г) 2 m

i + Vr 2

2 mc ²

v n ( r) = E * y n ( r) ,

где

E_n = E n | 1 +       I .                             (45)

V 2 mc )

Уравнение (44) является точным следствием исходного релятивистского уравнения (27) и представляет собой стационарное уравнение Шредингера для функции у _n ( r) для частицы массы m во внешнем потенциальном поле вида

U ( r ) = V ( r )

i + V * r !

2 mc ²

E n — собственные значения оператора Гамильтона

-        й2   9

н_к Г=-- V ² + V (F)

КГ

2 m

1 + V51

2 mcc

- — V² + U (F), 2 m

через которые величины En , входящие в формулу (43), выражаются по вытекающей из (45) формуле

E n = mc ²

*

1 + 2E2T - - 1 mc ²

Назовем величину U ( r), определяемую формулой (46), эффективной потенциальной энергией частицы во внешнем поле и рассмотрим ее некоторые характерные особенности.

Заметим, что если | е П | <<  mc ² , то, как следует из (48),

*2

E n "  E n - T n T .                        (49)

2 mc²

Таким образом, рассматриваемая нами квантовая релятивистская модель, прямым следствием которой является уравнение (44), свидетельствует,   что условием применимости стационарного уравнения Шредингера й2

- — V ² + V (Г)

2 m обычного

V n ⁽ r ) = E n V n ⁽ r ) ,

являются требования слабости поля и малости энергии возбуждения частицы в этом поле по сравнению с ее (частицы) энергией покоя: | V ( r) | <<  mc ², | E n | <<  mc ²; при этом второе требование, очевидно, эквивалентно нерелятивистскому приближению.

Однако интересно, что и в общем случае, т.е. при V ( Г )|~ mc² и | E n | ~ mc ², стационарные состояния частицы описываются уравнением, обладающим в точности такой же математической структурой, что и нерелятивистское стационарное уравнение Шредингера, отличаясь от него лишь заменой функции V ( r) на эффективную потенциальную энергию частицы U (г), которая, впрочем, весьма просто (линейно-квадратичным образом) связана с функцией V ( r ).

Это позволяет выдвинуть гипотезу , что используемые в современной физике выражения для потенциальной энергии частицы в электрическом (и, возможно, даже в гравитационном) поле, а также, не исключено, некоторые выражения, моделирующие ядерные силы, корректно описывают действие электрических, гравитационных и ядерных сил лишь в областях, где | V ( г) | <<  mc ² ; а реальный характер поля в любой его области и при практически любой энергии частицы со значительно более высокой точностью описывается «эффективной» функцией вида (46).

Теперь предположим для простоты, что поле, описываемое функцией V ( r ), является центрально-симметричным, так что V ( r ) = V ( r ) Тогда тем же свойством будет обладать и функция U ( r) : U ( r) = U ( r ). Ведем обозначения:

F^V =-V V (r) = -dVM er, F^U = -V U (e) = -dU(r) Г r, (51) dr dr где er — единичный вектор, направленный от источника (центра) поля вдоль радиуса к рассматриваемой точке пространства. Как следует из соотношений (51), величины FV и FU равны (с точностью до некоторого постоянного коэффициента, размерность и значение которого зависят от характера поля) силам, действующим на рассматриваемую частицу в поле, задаваемом функциями, соответственно, V(r) и U(r). При этом, как видно из тех же формул (51), положительный знак производной dV(r)/dr или dU(r)/ dr соответствует притяжению частицы к центру поля, а отрицательный знак этой производной – отталкиванию частицы от этого центра.

Дифференцируя функцию U ( r ) (46), получаем для F U :

—*

F u =

^^^^^^в

dU (r) — dr r

—

V ( r ) ) dV ( r ) — J V ( r ) ) ^{— 1 +} — 2 I—;— e r ^-l ^{1 +} — у I F V .

mc ) ^dr v mc )

Из (51) следует, что в центрально-симметричном поле, в котором V(r) > 0, направление «силы» FU всегда совпадает с направлением «силы» FV . Иными словами, эффективный потенциал в таком поле не изменяет характера действия (притяжения или отталкивания) поля на частицу. Если же V(r) < 0, то в точках, где |V(r)| > mc2, характер действия поля изменяется на противоположный (напомним, что здесь, как обычно, за нуль потенциальной энергии принимается ее значение при r ^ ^ , т.е. полагается, что V(r-^)- 0).

Следовательно, если во всей области слабого поля V(r) > 0 и dV(r)/ dr < 0, т.е. частица находится в поле сил отталкивания (как, например, электрон в поле антипротона или позитрон в поле протона), то и при приближении частицы к центру данного поля и попадании нее в область сильного поля отталкивательный характер этого поля не изменится, но отталкивание будет более «жестким», чем предсказывает зависимость V(r). Если же во всей области слабого поля справедливы неравенства V(r) < 0 и dV(r)/dr > 0 , т.е. если частица находится в поле сил притяжения (как, к примеру, электрон в атоме водорода или массивная (с m ^ 0) частица, помещенная в гравитационное поле), то при достаточном сближении данной частицы с центром поля силы притяжения неизбежно сменятся силами отталкивания. Таким образом, если эта особенность действительно имеет место и в случае гравитационного поля, то тогда гравитационный коллапс не может привести к стягиванию всего вещества, падающего на «черную дыру», в одну точку. И поскольку, по-видимому, природа не допускает сингулярностей, уже этот простейший пример можно рассматривать как важное свидетельство в пользу нашего предположения о том, что именно U(r), а не V(r), играет определяющую роль в микромире и физике высоких энергий.

Одна из возможных физических причин этого, по-видимому, состоит в самодействии реальных полей, роль которого возрастает по мере увеличения плотности энергии поля и постепенно становится определяющей, и которое формально проявляется в нелинейной зависимости от V функций Лагранжа, описывающих эти поля.

Вернемся к уравнению (44). Из равенств (43) и (48) следует, что стационарные решения модифицированного уравнения КГ (27) имеют следующий вид:

* n ⁽ r , t ) = V n ⁽ r ) exp

^^^^^^e

i 2

mc

h

V

1+-EL t mc

В случае слабого поля, когда | V ( r ) | << mc ² , второй член в квадратных скобках в формуле (44) представляет собой малую поправку. Поэтому в данном случае квантовый оператор Гамильтона H КГ можно представить в виде суммы гамильтониана Hl к) нулевого приближения и оператора возмущения W ( Г) :

ч = Н ⁽⁰⁾ + W г)                             ('54')

H КГ H КГ ⁺ W ^{( r} ) ,()

где й2                     - г2 г)

и(0)     h V2     -

H КГ --—V + V (r),     W (r)      2 ,

• 2 m2

и решать уравнение (47) с помощью известных [2,3,19,20] методов стационарной теории возмущений. Однако при этом необходимо не забывать, что полученные таким образом решения данного уравнения будут справедливы только в тех областях пространства, в которых имеет место неравенство |V(r )| << mc2. В частности, в случае электрона, находящегося в кулоновском поле ядра, это означает, что теория возмущений применима лишь при r >> re, где re – классический радиус электрона.

Решение модифицированного уравнения КГ для водородоподобного атома

В качестве примера применения стационарного варианта модифицированного уравнения КГ рассмотрим электрон (спин которого здесь мы учитывать не будем) или п- -мезон, находящиеся в связанном состоянии в электростатическом поле ядра протона. Это поле является сферически симметричным кулоновским, а потенциальная энергия рассматриваемой частицы (для определенности далее будем говорить об электроне) в данном поле описывается формулой

• V(r) = -^e— = -    .(56)

4ne0rr

Тогда

( 1 a^

U (r) = -ай c I------I.(57)

( r 2 mc _r ² J

При уменьшении r от значений r >> re, где re = — » 2,818-10-15 м — mc классический радиус электрона, функция U(r) (57) является отрицательной и монотонно убывающей при всех r > re , в точке r = re    она принимает свое минимальное значение

U (r = re) = Umin = — mc 2, а при дальнейшем уменьшении r она монотонно и неограниченно возрастает, принимая равное нулю значение в точке r = r0 = re /2 . Таким образом, на расстоянии r = re от ядра эффективное поле притяжения переходит в поле отталкивания, возрастающее по мере приближения электрона к ядру и представляющее для электрона бесконечно высокий потенциальный барьер. В результате оказывается, что электрон в стационарных связанных состояниях не может находиться слишком близко к ядру, и поэтому его волновая функция в точке r = 0 в этих состояниях должна обращаться в нуль. Заметим, что именно такое требование обычно накладывается «вручную» на волновую функцию при решении уравнения Шредингера, несмотря на то, что условия ограниченности и нормировки волновой функции допускают, вообще говоря, и отличное от нуля, но конечное значение этой функции в точке r = 0 .

Найдем точное стационарное решение модифицированного уравнения КГ (27) для атома водорода, предполагая, что масса ядра этого атома бесконечно велика. В этом случае функция U ( r ) выражается формулой (57), и уравнение (44) принимает вид:

С 2 2mc а а2 )   ._.

I V2 +—----- IVn (r) =---yn Vn (r).(58)

( Й r r2 J

Здесь r , А , ф - сферические координаты,

2 d22

V =^" + —  +^А(», ф), d r2 r d r r1

Д‘ ( А , ф ) = —¹f— sin А | + ¹--—-.            (60)

sin А (дА    дА J sin² Адф ²

Уравнение Шредингера (58) решается стандартным методом разделения переменных:

V n ⁽ r ) = V nlm ⁽ r) = ¹ X nl ⁽ Г ) ^Y lm № ф) ,                 ⁽⁶¹⁾

r где r-1xnl (r) - радиальная часть волновой функции уnlm (r), а Ylm (А, ф) - функции, называемые сферическими гармониками и удовлетворяющие дифференциальному уравнению [2,19–23]:

Д‘ ( А , ф ) Y lm ( А , ф ) + l ( l + 1) Y lm ( А , ф ) = 0 ,                 (62)

где l = 0,1,2,..., m = - 1 , - 1 + 1,..., - 1,0,1,..., l - 1, l .

Подставив выражение (61) в уравнение (58) и учитывая равенство (62), после несложных преобразований мы приходим к дифференциальному уравнению для функции x _nl ( r ):

d ²    2 mc a l ( l + 1) + a ²

+  ⋅- dr2    % r rг

X nl ⁽ r ) =-- ^n " X nl ^{( r} ).

Подчеркнем, что это уравнение – точное следствие исходного релятивистского модифицированного уравнения КГ (27) для случая кулоновского поля. Интересно, что оно очень близко к уравнению, которое получается в нерелятивистской квантовой теории атома водорода [2,3,19,20] и отличается от него лишь малой (по сравнению с величиной l (l +1)/ r2) поправкой (a / r)2, т.е., формально, заменой l (l +1) ^ l (l +1) + a2. Оно также отличается от уравнения [2]

" d ² + 2 E_nl a- l ( l + 1) -a ² ' dr ²     % c r       r ²

X nl ^{( r} )

( mc 2 ) 2 - E nl (% c ) 2

X nl ^{( r} ),

возникающего при решении рассматриваемой нами задачи на основе стандартного уравнения КГ. Это отличие, казалось бы, на первый взгляд, несущественно, но в действительности есть принципиально важный момент: противоположный, по сравнению с уравнением (64), знак перед a ² в числителе последнего члена в квадратных скобках уравнения (63), как мы увидим ниже, приводит к устранению еще одной трудности стандартной теории.

Отметим также, что уравнение (63) также возникает при решении нерелятивистской квантово-механической задачи о нахождении колебательно-вращательного спектра двухатомных молекул, взаимодействие атомов в которых моделируется потенциалом Кратцера [24,25].

Введем обозначения:

2 mE _п1 γ = - ^nl

У % ²

е I mc | о = ay I — I , l й )

P = ² Y r,

где [Y] = 1/ м, § - безразмерная константа, p - безразмерная радиальная координата. Тогда уравнение (63) запишется в виде:

d2   8_l (l +1) + a2 - £ d p2   p p2       4

X nl ⁽ r ) = ⁰ .

Следуя стандартной методике [26,27], найдем решение уравнения (66). Это уравнение имеет две особые точки: p = ^ и p = 0. В окрестности первой особой точки вторым и третьим членами в данном уравнении можно пренебречь, и тогда 4( d ² x _nl I d p ² ) = X nl , откуда

X nl ⁽ p ^)-ex P ⁽ -p ^/2) , если p >” . ⁽⁶⁷⁾ В окрестности особой точки p = 0 не расходящиеся решения должны иметь степенную зависимость от ρ :

X nl ( p )~ p^{X l} , где ^X i > ¹ , p> 0. (68) Подставляя (68) в уравнение (66), после простых преобразований и перехода к пределу p >  0 мы получаем характеристическое уравнение для определения показателя степени λ _l :

X _l ( X _l - 1) = l ( l + 1) + a ² , (69)

откуда находим:

1,            ,1 2

X/ = —+ 1 I l +— I + a >  1.

• ^l    2 К 2 J

С учетом зависимостей (67), (68), решение уравнения (66), пригодное во всей области значений p >  0 , можно записать в виде:

X_ri ( p ) = p^{X l}e ^{-p 12} f ( p ). (71) Подстановка (71) в уравнение (66) приводит, после несложных преобразований, к дифференциальному уравнению для функции f ( p ), называемому уравнением Куммера [28]:

p ут+(2X l -p) dr - fX l-^ d p2            d p l     Y2 J f (p) = 0 .

Его решение выражается через вырожденную гипергеометрическую функцию, или функцию Куммера [28,29]. Для того, чтобы решение Xnl (r) уравнения (66) убывало при r >^, необходимо, чтобы функция Куммера f (p) представляла собой многочлен конечной степени. Это условие выполняется, если выражение в круглых скобках в уравнении (72) будет равно нулю или целому отрицательному числу [28], т.е. если

λ l - ^δ =- n r ,                            (73)

Y 2

где n r = 0,1, 2, 3,... - радиальное квантовое число.

Из этого условия находим, с учетом равенств (65), допустимые значения параметра γ :

а [ mc 1

^{Y = Y} n = 77 7 71 I , ( л l + n r ) 7 я )

откуда, учитывая определение (65) у , получаем для E*_nl :

E

*

nl ⁼

_ 2    2

α mc

2( Л _; + n_r ) ² .

Перепишем формулу (75), подставив в нее выражение (70) для λ _l :

2    2

* а mc

E_nl = -

nr

1 ++

'     112      2

l + — I +а ²

- 2

В результате

стационарных получаем:

для возможных значений энергии E_nl частицы в состояниях, определяемых равенством (48), мы

E nl

= mc <

1 -а ²

1 n_r + +

i 11 ²       2

l +— I +а ²

2 )

- 2

- 1

.

Заметим, что это – точное выражение, полученное в рамках рассматриваемой нами модели без использования предположений о слабости поля, малости α и т.п.

Используя известные соотношения между вырожденной гипергеометрической функцией и обобщенными полиномами Лагерра L n ( p ) [28,29], решение f ( p ) уравнения (72) при условии (73) можно привести к виду:

f (p) ЙТГГЧ ^p) ■            (78)

Г(2Л l + nr) r где Г(z) - гамма-функция,

n

L n ( p ) = p^- a e ^p       ( p a ⁺ n e ^^p ).                        (79)

d ρ ⁿ

В результате, подставляя выражения (61), (71), (78) в формулу (53) и переходя, согласно соотношению (65), от ρ к размерной радиальной координате r, для набора функций Тnlm (r, Ф, ф, t), описывающих стационарные состояния заряженной массивной скалярной частицы в притягивающем кулоновском поле, получаем следующее выражение:

^Т nlm ⁽ ' , ^Ф , ф , t )

= const - r ^{X l 1} e ^{Y nir}f_nl ( r ) Y _lm ( Ф , ф )ехр

' - i 2 w^mc

v

1 +          t.

mc

, (80)

где параметры Xl, ynl и Enl определяются выражениями, соответственно, (70), (74) и (76), а функция fnl (r) - одной из эквивалентных формул f (r) = 1 - nr (2Ynlr) + nr (1 - nr) (Yr)! -

J nlV        b 1!      b (b +1)2!

- nr(1 - nr)(2 - nr) (2/^)3 + + n (bl -1)!    (2/^)nr( bl(bl +1)(bl + 2)      3!       "' 1 ; (bl + nr -1)! nr! ’

1-2X                     r(2X l)      d"'     2X,+ n,-1 -2X„,rx fnl (r) = r l exP (2Y nl') -          -------— (' l ' e nl ) ,

Г (2 Х l + " г ) dr" '

fnl (') = ГттЧ - L^l -1(2Y nl')

r (2 X l + " г ) ⁿ r

(здесь для краткости обозначено b_l = 2 X _l ).

Из формул (80), (81) с очевидностью следует, что при r ^ 0

функции Тnlm (r, Ф, ф,,) зависят от r по закону Тnlm ~ r^-1. И так как, согласно

(70), показатель степени λ _l

- 1 =

¹ Г ^²i + ^1)r + ^{4 a i}

-

2 _

положителен при всех допустимых значениях l = 0,1,2,... , все функции Т _nlm убывают при r ^ 0 и в точке r = 0 обращаются в нуль независимо от набора значений квантовых чисел n_r , l , m . Это значит, в частности, что основное состояние системы, состоящей из двух противоположно заряженных частиц является стабильным : ни одна из частиц «не упадет» на другую.

Заметим, что, в противоположность этому, аналогичные функции Тn(m (r, Ф, ф,,), являющиеся стационарными решениями стандартного уравнения КГ (1), полученного на основании функции Гамильтона (2), в s-состояниях, в которых «орбитальное» квантовое число l = 0, в точке r = 0 оказываются сингулярными при любых значениях nr [2]. И хотя в случае водородоподобных пионных атомов с зарядом ядра Ze эта сингулярность при малых значениях Z считается слабой, с ростом Z она быстро растет, и для таких атомов «с большими значениями Z она становится уже значительной, а отличие релятивистских функций от нерелятивистских становится существенным» [2]. При этом оказывается, что уже для атомов с малыми значениями Z сравнительно велика вероятность пребывания п- -мезона внутри ядра, так что в этом случае при вычислении волновых функций и энергии пионных атомов оказывается весьма важным учет конечных размеров ядра, т.е., фактически, отличия электрического поля ядра от кулоновского [2]. В то же время при l > 0, т.е. в p-, d- (и т.д.) состояниях, функции ТnС^ (r, А, ф, t) сингулярностей не имеют.

С точки зрения автора, наличие сингулярности у функций Т Пс00( r, А, ф, t) свидетельствует об их некорректности, не соответствии реальности. А поскольку они являются прямым следствием функции Гамильтона (2), то напрашивается вывод о физической некорректности также и этой функции Гамильтона. С другой стороны, поведение функций Тnlm (r, А, ф, t), полученных в рамках рассматриваемой нами модели, вполне физично при всех значениях квантовых чисел и во всей области значений переменных. Это обстоятельство, по мнению автора, является еще одним свидетельством в пользу функции Гамильтона (26) и модифицированного уравнения КГ (27).

Исходя из точной формулы (77) и учитывая, что а2 << 1, найдем приближенное выражение для энергии частицы Enl с точностью до членов порядка а4 . Поскольку

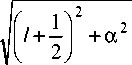
1 а ²       а ⁴

l + - +----

2 2 1 + 1 (2 1 + 1) 3

+ ... ,

то, как легко найти,

E nl

₂ mc ²    4 mc ² ( 1 1

-а —— + а    I -

2 n ²        2 n ³ I k 4 n

где введены следующие обозначения: k = l + -2 и n = nr +1 +1

- главное квантовое число, n = 1,2,3,....

При этом орбитальное

квантовое число l может принимать лишь следующие значения: l = 0,1, 2,3,..., n - 1.

Заметим, что если в формуле (85) сделать замену α ² → ( Z α )² , то она будет справедлива не только для водородоподобного пионного атома, но и для водородоподобных ионов с зарядом ядра иона Ze , где 1 ≤ Z ≤ 25 .

Обсуждение полученного решения

Проанализируем полученное выше решение модифицированного уравнения КГ. Сразу же обратим внимание на то, что первый член в формуле (85) в точности совпадает с результатом нерелятивистской квантовой механики [2,19,20], основанном на решении уравнения Шредингера, так что второй ее член представляет собой релятивистскую поправку, принципиальным отличием которой является ее зависимость не только от главного квантового числа n , но и от орбитального квантового числа l .

Сравним формулу (85) с соответствующим выражением, вытекающим из релятивистской квантовой теории, основанной на стандартном уравнении КГ [2]:

(ст) E_nl

-α

mc ²     4 mc ² Г 1   3

a I

2 n ²       2 n ³ I k 4 n

Эти формулы отличаются друг от друга, во-первых, знаком перед поправочным релятивистским членом и, во-вторых, численным коэффициентом в последнем слагаемом (заметим, что выражения в круглых скобках и в формуле (86), и в формуле (77) всегда положительны). Следовательно, учет релятивистских эффектов и в теории, основанной на обычном уравнении КГ (4) (назовем ее «S-теорией»), и в развиваемой в данной работе теории («М-теории»), снимает имеющее место в нерелятивистском приближении вырождение уровней энергии по l , приводя к появлению «тонкой структуры» этих уровней и их смещению относительно исходного уровня. При этом количество подуровней тонкой структуры оказывается одинаковым и в М-, и в S-теории. Однако, согласно предложенной здесь М-теории, подуровни тонкой структуры оказываются смещены вверх относительно исходного уровня энергии, в то время как решения обычного уравнения КГ предсказывают их смещение вниз. Такое различие в направлении смещения подуровней вполне объяснимо, поскольку эффективный потенциал U (r) (57), входящий в модифицированное уравнение КГ, уменьшает ширину потенциальной ямы, в которой находится заряженная частица, что, как известно, приводит к смещению энергетических уровней частицы вверх. При этом, как следует из формулы (85), наибольшее смещение имеют подуровни с l = 0, а меньше всего смещаются уровни с l = n -1. Действительно, согласно нашей теории,

• ₂    mc ₄ mc

E n ,0 “^-a ~~2" ^{+ а} тгС ⁸ n - 1) ,

2 n 8 n

E n , n - 1 "-a 2	mc 2	+ a 4	mc 2	f 6 n + 1
	2 n 2		8 n 4	E 2 n - 1,
так что E n , 0 >  E n , n - 1 . В то время как по			S-теории
(ст)         2 E n ,0      a	mc 2	-a 4	mc 2	(8 n - 3)
	2 n 2		8 n 4
(ст)           2 n , n - 1	mc 2	-a 4	mc 2	f 2 n + 3'
	2 n 2		8 n 4	E 2 n - 1,

• и, следовательно, E^ <  Е^с т - 1 .

Однако, поскольку зависимость от l = к - 1/2 в формулах (85) и (87) одинакова, «ширина тонкой структуры», т.е. разность энергий |A E n | состояний с минимальным и максимальным значениями орбитального квантового числа l = 0 и l = n - 1 при заданном значении n в обеих теориях также оказывается одинаковой:

| A E n | = | E n , i - 1 - E n ,o | = |a E П ^ст)| = a 4 2mC² • ^f      1 .            (90)

n ³ E 2 n - 1 7