Эффективное моделирование квантовых алгоритмов на симуляторах классической архитектуры

Эффективное моделирование квантовых алгоритмов на симуляторах классической архитектуры / П. В. Зрелов [ и др.] // Системный анализ в науке и образовании: сетевое научное издание. 2022. № 1. C. 42–54. URL :

Zrelov Petr V. Effective simulation of quantum algorithms on simulators of classical architecture. System Analysis in Science and Education, 2021;(1): 42–54(In Russ). Available from:

В настоящее время квантовое моделирование на классическом компьютере представляет особый интерес, поскольку вычисления на современных квантовых компьютерах имеют ограничения в виде небольшого числа кубитов, наличия ошибок и отсутствия эффективного способа коррекции этих ошибок. Вследствие этих ограничений использование универсальных квантовых компьютеров для решения практически значимых задач вероятно станет эффективным не ранее, чем через 10 или даже 20 лет. Однако квантовые симуляторы на основе различных архитектур (атомных, молекулярных, оптических) могут быть полезны уже лет через 5 [1]. И на данный момент, судя по всему, это направление является наиболее важным. Существуют реализации от Google , IBM , Rigetti , Intel , D-Wave [2-6]. Одновременно развивается направление, связанное с программными квантовыми симуляторами для вычислений на компьютерах классической архитектуры с использованием CPU и GPU [7].

В настоящей работе исследуется эффективность использования квантовых программных симуляторов для квантовых алгоритмов (КА). Для решения этой задачи были выбраны симуляторы QuEST [8] и Qiskit [9], позволяющие использовать как CPU (например, с использованием библиотеки для параллельного программирования OpenMP ), так и графические вычислители GPU . Эксперименты проводились на суперкомпьютере «Говорун» [10] в Лаборатории информационных технологий им. М. Г. Мещерякова Объединенного института ядерных исследований (ЛИТ ОИЯИ). Реализация квантовых алгоритмов на симуляторах с использованием классической архитектуры требует экспоненциального масштабирования памяти и времени вычислений [11].

Проведенные вычисления показали, что при моделировании на GPU можно достичь большего ускорения по сравнению c расчетами на CP U.

Следует отметить, что наибольшего ускорения расчетов, по утверждению компании NVIDIA , можно достичь с использованием нескольких графических процессоров [12-14], что было продемонстрировано компанией с помощью нового симулятора cuQuantum – было сымитировано 3375 кубитов на платформе NVIDIA DGXSuperPod ™ [15, 16].

Настоящее исследование не включает результаты, полученные с использованием симулятора cuQuantum .

Квантовые алгоритмы и их проектирование

Квантовые вычисления являются одним из наиболее бурно развивающихся направлений квантовых сквозных технологий. Квантовое моделирование обещает найти применение при решении целого ряда проблем физики конденсированных сред, физики высоких энергий, атомной физики, квантовой химии, космологии, машинного обучения, искусственного интеллекта [17, 18].

Квантовые компьютеры, доступные в настоящее время, называют «зашумленными» квантовыми компьютерами промежуточного масштаба1. Они реализуют, как правило, от 50 до 100 кубитов, вследствие присутствия шумов при вычислениях возникают ошибки, а возможность их коррекции отсутствует.

Наряду с созданием квантовых компьютеров, одним из важных направлений является направление, связанное с разработкой алгоритмов для этих компьютеров, основанных на принципах, отличных от принципов классических алгоритмов.

Существуют различные научные подходы к формализации преобразований входных данных для вычисления выходных данных с использованием квантовых ресурсов. Модель квантовых вычислений определяется базовыми элементами, на которые декомпозируются вычисления [19].

Основной моделью, имеющей практическое значение, является гейтовая модель [20, 21]. В этой модели вычисления разбиваются на последовательность из нескольких кубитных квантовых гейтов (вентилей). Это модель вычислений, в которой биты заменяются кубитами, а логические преобразования – конечным набором унитарных гейтов, которые могут аппроксимировать любую произвольную унитарную операцию.

Алгоритм, выполненный в одной из моделей квантовых вычислений называется квантовым алгоритмом (КА). Разработка КА основана на принципах, отличных от принципов классических алгоритмов. Даже классические алгоритмы должны быть приведены в специальную (обратимую) форму, прежде чем их можно будет запустить на квантовом компьютере.

Визуализация типичного рабочего процесса квантового алгоритма на квантовом компьютере с гейтовой моделью показана на рисунке 1. Особенностью этого процесса является конструирование алгоритма с помощью так называемых квантовых схем.

Рис. 1. Визуализация типичного рабочего процесса квантового алгоритма на квантовом компьютере с гейтовой моделью

Выбор КА2 определяется характером задачи. На следующем шаге КА представляется в виде квантовой схемы, представляемой в виде набора квантовых гейтов3. Скомпилированная квантовая схема может быть выполнена либо на квантовом процессоре, либо реализована с помощью симулятора квантового компьютера.

Среди всего множества КА есть алгоритмы, имеющие явные преимущества перед известными классическими алгоритмами. Основной группой таких алгоритмов являются алгоритмы квантового поиска (АКП) [24, 25, 26]. Особенностью данных алгоритмов является достаточность 75% вероятности для выбранного решения (в отличии от классического метода достоверного поиска решения с вероятностью 1).

Общая структура КА

На рисунке 2 показана общая структура квантовой схемы.

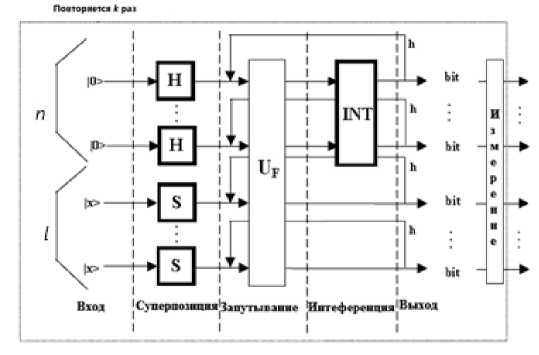
Рис. 2. Общая структура КА

Процесс проектирования КА включает матричную форму трех квантовых операторов: суперпозиции, квантовой запутанности (или квантового оракула) и интерференции. Оператором суперпозиции является тензорное произведение n операторов Адамара и l операторов тождественного преобразования. Полученный таким образом оператор действует на первые n кубитов (первый регистр), создавая их суперпозицию, и действует тождественно на последние l кубитов (второй регистр), оставляя его без изменений. Вид оператора запутывания UF зависит от свойств исходной функции f. Оператор интерференции зависит от рассматриваемого алгоритма. Оператором интерференции могут выступать, например, квантовое преобразование Фурье, оператор Адамара и другие.

КА воздействует на исходный базисный вектор для генерации суперпозиции базисных векторов в качестве выходных данных. После создания суперпозиции выполняется измерение для извлечения информации об ответе. В квантовой механике измерение — это недетерминированная операция, которая выдает на выходе один из базисных векторов во входной суперпозиции. Вероятность того, что каждый базисный вектор будет результатом измерения, зависит от его амплитуды вероятности во входящей линейной комбинации.

Квантовые гейты и операция измерения составляют квантовый блок, который повторяется k раз, чтобы создать набор из n базисных векторов. Поскольку измерение является недетерминированной операцией, эти базисные векторы не обязательно будут идентичными, и каждый базисный вектор кодирует часть информации, необходимой для решения задачи. Последняя часть алгоритма включает в себя интерпретацию собранных базисных векторов, чтобы получить окончательный ответ для исходной задачи с некоторой вероятностью.

На рис. 3 показана типовая структура КА.

_Ответ                                                                       Проблема

^NT                                              V

|Ф/in) = [(Интерференция)(Квантовый оракул)](Суперпозиция)|^пМаг )

Рис. 3. Структура КА

Сформировать разные модели квантовых вычислений можно, выбирая различные виды оператора U F .

В общем виде модель квантовых вычислений состоит из следующих этапов:

• -    приготовление начального (классического или квантового) состояния |^ j_nitiai );

• -    выполнение преобразования Адамара ( H ) для начального состояния с целью формирования состояния суперпозиции;

• -    применение оператора запутанных состояний или оператора квантовой корреляции (квантового оракула) к состоянию суперпозиции;

• -    применение оператора интерференции;

• -    использование оператора измерения для результата квантовых вычислений |ф /;_п ).

Процесс проектирования квантового алгоритма, как следует из рис. 2 и 3, состоит из матричной формы представления трех операторов [27]: Sup – суперпозиции, U F – квантовой корреляции (запутывания) или квантовый оракул и Int – интерференции.

В общем виде структуру квантового алгоритма, представленного на рис. 3, можно описать следующим образом:

С = [(/nt ® п/) • ШИГ' + 1 • [пН ® mS],                        (1)

где I – тождественный оператор, символ ⊗ обозначает тензорное произведение, H – оператор Адамара, S обозначает I или H в зависимости от задачи. Основой квантового блока является квантовый гейт U F , который зависит от свойств матрицы и применяется в алгоритме h+ 1 раз. Первая часть процесса проектирования – это выбор типа оператора в формуле (1), зависящего от проблемы запутывания. Оператор суперпозиции большинства АКП может быть выражен следующим образом:

Sup

n

® H к i=1   7

m

® ® S

к i =1  7

где n и m – количество входов и выходов соответственно. Оператором может быть или оператор Адамара, или тождественный оператор в зависимости от алгоритма (см. таблицу 1).

Табл. 1. Параметры операторов суперпозиции и интерференции основных АКП

Алгоритм	Суперпозиция	m	Интерференция
Гровера	nH ® H	1	D n ® I
Шора	nH ® nI	n	QFTn ® nI

QFT n – квантовое преобразование Фурье, D n – диффузия (инверсия относительно среднего).

Вычислительные модели алгоритмов квантового поиска

Основная сложность моделирования КА на классическом компьютере состоит в том, что ядром КА является унитарная матрица, размерность которой возрастает экспоненциально при линейном увеличении размерности квантовой системы.

На текущий момент существуют различные подходы к разработке АКП [28, 29, 30, 31]. Авторы работы [32] выделяют среди них следующие:

• 1)    Матричный подход, основанный на матричном представлении квантовых операторов. Этот подход является более стабильным и точным, но требует много памяти компьютера, что осложняет моделирование алгоритмов с большим числом кубитов.

• 2)    Подход, основанный на алгоритмах, в которых элементы матрицы вычисляются по «требованию». Этот подход не требует выделения памяти компьютера для квантовых операторов, поскольку вычисляет каждый компонент только тогда, когда он требуется. Подход позволяет использовать немного больший размер входных данных по сравнению с матричным подходом. К недостаткам можно отнести необходимость хранения в памяти компьютера вектора состояний и необходимость дополнительного изучения структуры операторов.

• 3)    Проблемно-ориентированный подход. Количество переменных, используемых для представления переменной состояния в этом подходе, является постоянным. Фиксированное число переменных для представления вектора состояния позволяет пересмотреть традиционную схему моделирования квантового поиска. Операции матричного произведения заменяются арифметическими операциями с фиксированным числом параметров независимо от числа кубитов.

В данной статье рассматриваются квантовые симуляторы Qiskit и QuEST , которые реализуют первый подход в этом списке, т.е. тот, что основан на представлении квантовых матричных операторов.

Квантовый поиск Гровера

Задачу квантового поиска Гровера можно сформулировать следующим образом: из списка N предметов требуется определить один, удовлетворяющий какому-либо специфическому свойству.

На рисунке 4 приведена принципиальная схема алгоритма Гровера. Подробное описание алгоритма Гровера и его модификации приведены в [33-37].

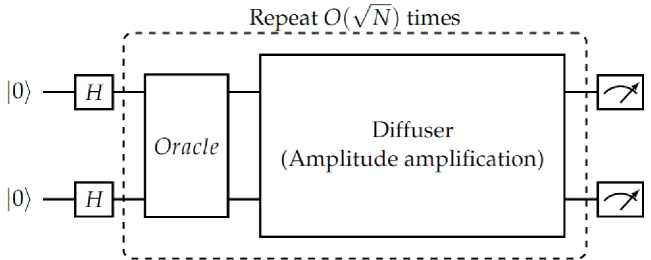
Рис. 4. Принципиальная схема алгоритма Гровера

Выбор симуляторов

Среди большого количества квантовых программных симуляторов [38-40] одними из наиболее популярных на текущий момент являются:

• -    платформа Qiskit для квантовых вычислений с открытым исходным кодом. Разработана с учетом возможности расширения и поддержки исследований на квантовых системах IBM , основанных на сверхпроводящих кубитах, квантовых системах с ионной ловушкой IonQ и квантовых вычислительных устройствах AQT .

• -    Конструктор квантовых схем Cirq , который можно использовать с квантовыми устройствами Google и с другими квантовыми симуляторами.

• -   PyQuil , который можно использовать с квантовыми системами Rigetti .

• -    ProjectQ для поддержки исследований на квантовых системах IBM , AQT , AWS Braket , IonQ .

Использование перечисленных выше квантовых устройств либо достаточно дорого, либо ограничено небольшим количеством доступных кубитов.

В силу описанных ограничений запуск симуляции на классических компьютерах представляет особый интерес.

Симуляторы на классической архитектуре с использованием CPU и GPU

Из внушительного списка квантовых симуляторов на классической архитектуре были выбраны те, которые позволяют использовать OpenMP и GPU .

В настоящее время на CPU для квантовых симуляторов доступны возможности запуска на многопроцессорных системах, причем некоторые из симуляторов способны работать и в распределённой вычислительной среде. Это открывает возможности симулировать системы с достаточно большим количеством кубитов.

Масштабируемость процесса симуляции на GPU развита меньше. Недавно NVIDIA представила собственный квантовый симулятор cuQuantum , который может работать на нескольких графических процессорах, связанных высокоскоростным интерфейсом NVLink . Один GPU с 32 Гб оперативной памяти может выполнить симуляцию 31 кубита. Вектор состояния для системы с бόльшим количеством кубитов уже не может поместиться в память одного GPU , и для дальнейшего масштабирования на каждый новый кубит требуется удваивать количество используемых GPU . В таком случае, каждый GPU содержит часть вектора состояния и может применять гейты независимо. Если часть вектора состояния хранится на другом GPU , то применение гейта к полному вектору может потребовать передачи значительного объема данных, измеряемого гигабайтами, а это возможно только при наличии быстрого соединения между GPU . NVLink позволяет производить очень быстрый обмен данными, что невозможно при использовании нескольких GPU , подключенных к разным сокетам, или при использовании распределённых систем.

QuEST – один из первых симуляторов, использующих многопоточность, распределенные вычисления и GPU-ускорители [41]. QuEST – это симулятор, представляющий чистые квантовые состояния с помощью векторов состояний и смешанные состояния с помощью матриц плотности. Количество памяти необходимое для выполнения вычисления для вектора состояния можно посчитать по формуле b*2{qubits-29} (GiB), где b = 8 с двойной точностью. Следует отметить, что одновременное использование нескольких серверов или даже нескольких графических процессоров на одном сервере невозможно.

Qiskit – самый популярный квантовый симулятор на данный момент. Он позволяет проводить моделирование на CPU и GPU , а недавно появилась возможность использовать OpenMP и CUDA [42]. Он также предоставляет возможность использовать различные методы моделирования. Одним из них является MPS ⁴. Квантовое состояние в этом подходе описывается следующим образом:

, где состояния |0〉 , |1〉 принадлежат двумерному Гильбертовому пространству. Этот подход [43] дает преимущество, когда в квантовой цепи низкая степень запутанности. MPS может увеличить скорость и уменьшить количество требуемой памяти, однако, это возможно при условии, что не требуется выводить вектор состояния, потому что эта операция экспоненциально зависит от времени. Использование этого метода на простых квантовых схемах позволяет выполнять моделирование более чем на пятистах кубитах.

QSim [44] содержит полный симулятор вектора состояния Шрёдингера и гибридный симулятор Шредингера-Фейнмана. Позволяет запускать симуляцию на процессоре с использованием OpenMP и GPU. На момент публикации cuQuantum от NVIDIA , имеющий большой потенциал для моделирования, интегрировался в QSim . Квантовый симулятор QSim поддерживается Google , в работе [45] приведены результаты его сравнения с квантовым устройством .

Аппаратное обеспечение

Как было упомянуто выше, эксперименты проводились на суперкомпьютере Говорун в ЛИТ ОИЯИ.

Эксперименты с графическим процессором проводились на DGX -1 [46] с 8 X NVIDIA Tesla ® V 100 16 GB / GPU , 512 GB DDR 4 RDIMM , 4 X 20- Core Intel ® Xe on ® E 5-2698 v4 2.2 GHz .

Моделирование с использованием центрального процессора проводилось на следующих конфигурациях:

• -  8 серверов с 4 X 72- Core Intel® Xeon Phi™ 7290 1.50 GHz , 96 GB DDR 4;

• -  4 сервера с 4 X 24- Core Intel® Xeon® Platinum 8268 2.90 GHz , 192 GB DDR 4.

Моделирование квантовых алгоритмов на компьютерах классической архитектуры

На этапе тестирования симуляторов QuEST и Qiskit были произведены эксперименты с использованием от 2 до 31 кубита, чтобы получить надлежащий масштаб для наблюдения за результатами. Для анализа результатов рассмотрим диапазон от 22 до 30 кубитов. Для меньшего количества кубитов симуляция занимает незначительное время. Симуляции для большего количества кубитов ограничены памятью.

При разработке схемы тестового алгоритма мы воспользовались работой Google [47], произведя некоторые упрощения (см. рис. 5), и используя 100 повторений, а это значит, что к каждому кубиту в алгоритме применяется около 800 гейтов.

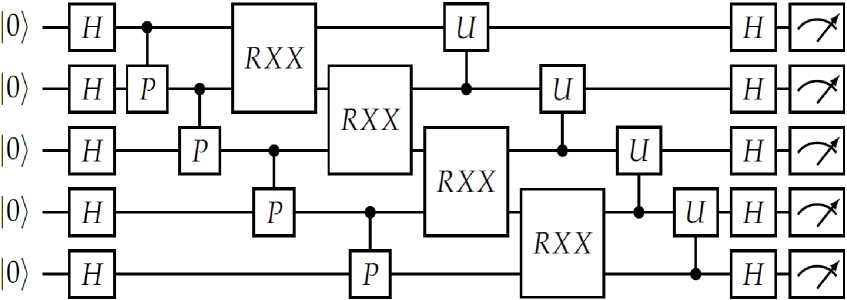
Рис. 5. Квантовая схема тестового алгоритма

Схема сконструирована таким образом, чтобы можно было корректно сравнить два симулятора, потому что не все квантовые гейты для более сложных задач в рассматриваемых симуляторах реализованы одинаково. Например, алгоритм Гровера может быть реализован на различных симуляторах по-разному, что не позволяет произвести объективное сравнение работы данного алгоритма на разных симуляторах.

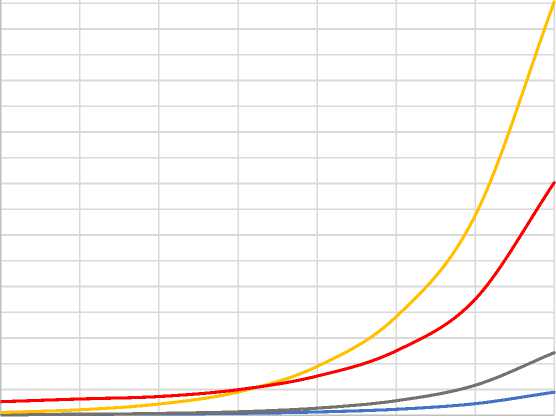
На рисунке 6 представлены усредненные значения времени выполнения тестового алгоритма на обоих рассматриваемых симуляторах как на CPU , так и на GPU .

Усредненные значения времени выполнения алгоритма для каждого

1700,00

1600,00

1500,00

1400,00

1300,00

1200,00

1100,00

о 1000,00

»г 900,00

S „

700,00

600,00

500,00

400,00

300,00

200,00

100,00

0,00

кубита

22       23       24       25       26       27       28       29

количество кубитов

• <      ■ Qiskit

GVR DGX (GPU) 100 cycle

• -    ■ QuEST

GVR DGX (GPU) 100 cycle

^^^^^^^^ш QuEST

GVR KNL (SINGLE CPU + 284 thread)

^^^^^^^^ш 1Q0is0kcitycle

GVR KNL (SINGLE CPU + 284 thread) 100 cycle

Рис. 6. Время выполнения тестового алгоритма на QuEST и Qiskit (CPU и GPU)

На обоих симуляторах на GPU по сравнению с CPU скорость выполнения алгоритма выше. Однако на QuEST нельзя произвести симуляцию более 29 кубит на GPU в силу ограничения памяти суперкомпьютера. Также стоит отметить, что Qiskit заметно быстрее QuEST на CPU со всей возможной параллелизацией.

Алгоритм Гровера (см. рис.4) также был реализован на обоих симуляторах (см. рис. 7).

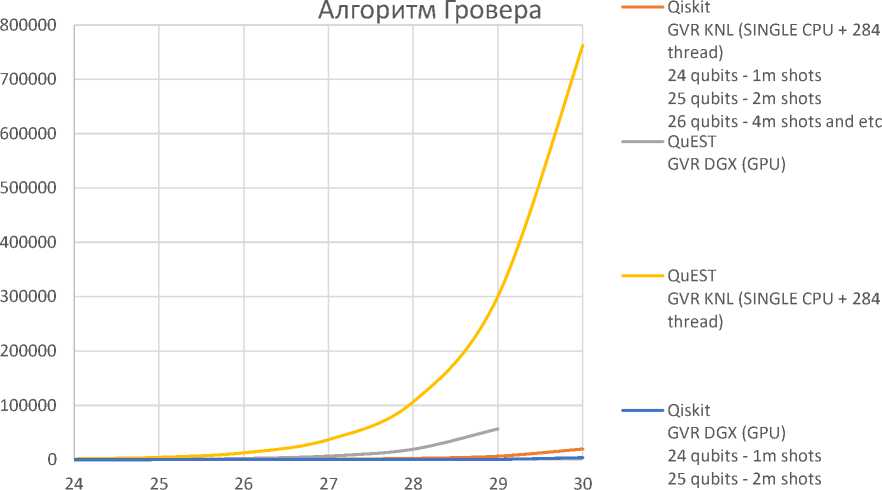
количество кубитов                             26 qubits - 4m shots and etc

Рис. 7. Время выполнения алгоритма Гровера на QuEST и Qiskit (CPU и GPU)

На рисунке 7 представлены усредненные значения времени выполнения алгоритма Гровера на обоих рассматриваемых симуляторах как на CPU , так и на GPU . Для 24 кубит – 1 shots , для 25 – 2 shots , для 26 – 4 shots и т.д., shots – количество запусков алгоритма.

Основной результат: Наименьшие временные затраты при выполнении данного алгоритма показывает Qiskit , а скорость выполнения на GPU меньше, чем на CPU .

Заключение

Моделирование квантовых алгоритмов на симуляторах с использованием классической архитектуры в эпоху NISQ представляется перспективным еще на достаточно долгий период, вероятно, до момента появления квантовых процессоров с количеством кубитов более 10⁵ и корректируемыми ошибками. До этого момента разработка и тестирование КА на симуляторах с использованием классической архитектуры хотя и ограничено памятью компьютера или суперкомпьютера, но позволяет применять КА для решения ряда задач в самых различных областях: квантовой химии, развития нанотехнологий, сбора и обработки экспериментальных результатов для интеллектуального управления различными системами ускорителя в мега-сайнс проекте НИКА [48], квантового глубокого машинного обучения в робототехнике и др.

Выбор квантовых симуляторов для реализации вычислений на суперкомпьютере Говорун, позволяет приступить к формированию библиотеки КА для решения инженерных задач. Особое место в данной библиотеке отводится поисковому алгоритму Гровера, матричная форма которого была реализована на обоих симуляторах. В дальнейших планах – реализация быстрых модификаций алгоритма Гровера и других КА, формирующих ядро библиотеки для решения инженерных задач.

Данная работа была проведена в рамках гранта Минобрнауки РФ №075-10-2020-117 «Сверхтяжелые ядра и атомы: пределы масс ядер и границы Периодической Таблицы Д. И. Менделеева».