Эффективное возбуждение пакетов мод идеального градиентного волновода с заданными фазовыми скоростями
Автор: Бахарев Максим Александрович, Котляр Виктор Викторович, Павельев Владимир Сергеевич, Сойфер Виктор Александрович, Хонина Светлана Николаевна
Журнал: Компьютерная оптика @computer-optics
Рубрика: Методы и элементы компьютерной оптики
Статья в выпуске: 17, 1997 года.
Бесплатный доступ
В данной работе разработан подход к повышению эффективности возбуждения мод градиентного волновода с помощью дифракционных оптических элементов (ДОЭ) в задачах уплотнения каналов волоконно-оптической связи, рассмотренных в [1]. Предложена модификация итерационного алгоритма [2], позволяющая существенно повысить эффективность формирования заданного модового состава и вместе с тем избежать уширения импульса, возникающего из-за межмодовой дисперсии [3], в каждом канале связи. Вводится понятие инвариантного модового пакета - амплитудно-фазового распределения специального вида, обладающего рядом свойств мод лазерного излучения. Приведены результаты вычислительных экспериментов по расчету и моделированию дифракционных оптических элементов, формирующих инвариантные модовые пакеты в заданных порядках дифракции, а также по прохождению сформированных пучков через Фурье-каскад.
Короткий адрес: https://sciup.org/14058348
IDR: 14058348
Текст научной статьи Эффективное возбуждение пакетов мод идеального градиентного волновода с заданными фазовыми скоростями
В [1] рассмотрена принципиальная возможность повышения информационной емкости каналов связи волоконно-оптических систем с помощью селективного возбуждения мод градиентного оптоволокна. Однако, существенным недостатком элементов, предложенных в [1] для возбуждения заданных гауссовых мод или групп мод (моданов), является их низкая энергетическая эффективность, связанная с появлением паразитных дифракционных порядков. Энергетическая эффективность однопучковых моданов, рассмотренных в [1], не превышала 10-33%.
В [2] был предложен итерационный метод расчета фазовых дифракционных оптических элементов, согласованных с несколькими модами, позволяющий достигать значения энергетической эффективности 85-90%. Метод [2] использует в качестве свободных параметров фазовые сдвиги между формируемыми модами в плоскости формирования модовых пучков и значения отсчетов фазовой функции рассчитываемого элемента в плоскости ДОЭ.
ления n ( X, y ) , волновые фронты мод являются
-
1. Фазовая скорость мод лазерного излучения
Для градиентного волоконного световода с поперечно-неоднородным показателем прелом-
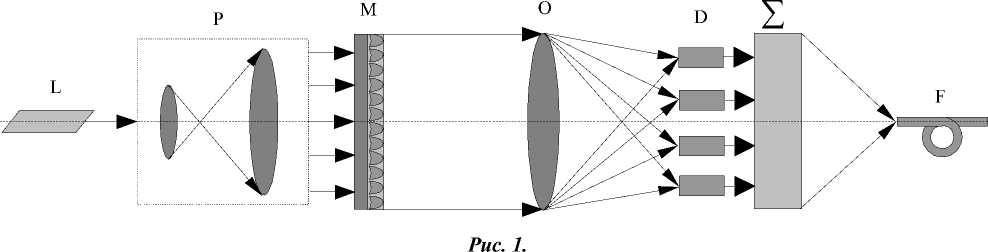
Однако, в случае небольшого числа каналов (25) свободных параметров в плоскости формирования модовых пучков может оказаться недостаточно для работы итерационной процедуры [2], что приведет к ощутимой ошибке формирования заданного модового распределения. На Рис. 1 представлена схема возбуждения оптоволокна с селективной модуляцией мод с помощью модана, предложенного в [2] : L - лазер, P - блок коллиматора, M - многопучковый модан, О - линза, S - оптический сумматор мод, D - оптические модуляторы, F - оптическое волокно. В данной работе с целью увеличения числа свободных параметров предлагается использовать для реализации отдельного информационного канала пакеты гауссовых мод с одинаковой фазовой скоростью распространения. Число свободных параметров (фазовых межмодовых сдвигов) по сравнению с подходом [2] возрастает в m раз, где m - число мод в каждом пакете. В то же время, использование пакета мод с одинаковой фазовой скоростью для реализации отдельного информационного канала позволит избежать уширения импульса, вызываемого межмодовой дисперсией [3].
плоскостями, а оператор распространения связы вает решение <у(X, y, z) уравнения Гельмгольца
V 2ro ( x , y , z ) + 8 ю( x , y , z ) + n 2 ( x , y ) ■ k2 ■ ro ( x , y , z ) = 0 (1) d z 2
с граничным значением
^ z = o = ®(x , y ,0 ) ,
где V±
( d 5) ’fl (5 x 5 y )
поперечный оператор Га
мильтона, а монохроматическое поле описывается в скалярном представлении комплексной амплитудой ® ( х , У , z ) .
Моды поперечно-неоднородного волоконного световода определяются из уравнения [1]:
V i ¥ pl ( х , У )+[ k 2 n 2 ( х , У )- ^ pi \v pl ( х , У ) = 0, (2) где ¥ pl ( х , y ) - комплексная амплитуда моды с номером p , I . Для любого расстояния z имеем:
^(х,У,z) = Ypi ’Vpi(x, У) (3)
Y pi = exp[(z p pi +a pi )■ z ], где Ppi - постоянная распространения, api - ко эффициент затухания моды ¥pi•
Собственными функциями оператора рас- пространения света в градиентном оптическом све- товоде с квадратичным распределением показателя преломления
П 2 ( Г ) = n 2
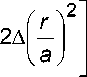
I 2 . 2 „r = д/х + У - a
A - константа, являются функции Гаусса-Эрмита и обобщенные функции Гаусса-Лагерра [1].
Обобщенные моды Гаусса-Лагерра опреде ляются следующим выражением:
l
I г I Г 2 r 2)
¥ pi(х, У) = Epi ----I ■ Lp I — I- exp r2
CT 2
■ exp [ ± ii a ] ,(5)
где a - полярный угол вектора (X, y), r = V X2 + y2 , L lp (.) - обобщённый полином Ла герра, ст - фундаментальный радиус моды,
F 2
E ы =--, = - нормировочная константа.
СТ/ 2п-1 !Cp+1
Моды Гаусса-Эрмита определяются соотношением:
V pi ( х . У ) = E pi ■ Hp 1 ^2 х- ст
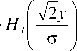
■ exp
X 2 + У 2 ст 2
где Hp (.) - полином Эрмита степени p, ст - фун- даментальный радиус моды ГЭ,
E pi =
2 к- 2 p + 1 ■ p ! ■ i ! ’
Фазовая скорость ep\ распространения гауссовых мод определяется уравнением [1]
P pi Ik2 n 2 - ( rp. + 1 ) , (7)
V CT '
где T pi =p+i для мод Гаусса-Эрмита и r pi =2p+i для мод Гаусса-Лагерра.
Напомним замечательные свойства гауссовых мод [1,4]:
-
1) являясь собственными функциями распространения света в градиентном волокне, гауссовы моды сохраняют амплитудно-фазовую структуру при распространении в свободном пространстве;
-
2) гауссовы моды сохраняют взаимную ортогональность при распространении в градиентных средах и свободном пространстве;
-
3) гауссовы моды сохраняют амплитуднофазовую структуру при прохождении Фурье-каскада.
-
2. Построение итерационной процедуры расчета дифракционного оптического элемента, согласованного с инвариантными модовыми пакетами
Из (3) и (7) следует, что в отсутствие затухания (api=0) линейная комбинация нескольких гауссовых мод, для которых выполняется rpi=const (8)
при распространении ведет себя фактически как отдельная мода лазерного излучения: амплитуднофазовая структура пучка будет сохраняться, а комбинации, соответствующие различным значениям r pl ,будут взаимно ортогональны, так как не могут содержать мод с одинаковой парой индексов (p,i) . Амплитудно-фазовые распределения, описываемые линейными комбинациями гауссовых мод, удовлетворяющих (8), будем называть инвариантными модовыми пакетами .
При передаче информации по отдельным каналам с помощью инвариантных модовых пакетов в идеальном градиентном волноводе с профилем (4) не будет возникать межмодовой дисперсии и, следовательно, уширения импульса, вызываемого межмодовой дисперсией [3].
С другой стороны, выбор инвариантных модовых пакетов в качестве носителей информационных каналов позволяет использовать в качестве свободных параметров для итерационной процедуры [2] не только фазовые сдвиги между отдельными инвариантными модовыми пакетами, но и межмодовые фазовые сдвиги внутри каждого пакета.
Нам необходимо вычислить фазу ф (x,y) оптического элемента, освещаемого Гауссовым пуч- ком с распределением амплитуды A(x,y). Элемент формирует моды (пакеты мод) в дифракционных
заменяются коэффициентами
порядках, определяемых векторами пространствен-
(1) (2)1
ных частот несущих ( v p , V p/ ) , где p, l - порядковые номера моды. Функция комплексного пропускания такого элемента должна подчиняться следующему соотношению [2]:
A ( x , y ) • ехр [ / ф ( x , y )] = (9)
= Д J0 C pl V pl ( x , У ) • exp [ - i 2 n(v (pi x + x ^ ) y )]
С ( k ) pl
используя сле-
дующее правило:
с ( k)=в с( k )lc( k )Г1 гм)
C pl B pl C pl I C pl I (14)
где V pl ( x . У ) - гауссова мода с порядковыми но-
где B pl положительные числа, характеризующие распределение энергии между модами.
Коэффициент C ( k ) подставляется в (9). Как итоговый результат, мы получаем функцию F k + 1 ( X , У ) , аргумент которой сохраняется как оценка фазы:
мерами ( p, l ). Модуль коэффициента C pl выбирается из условия желаемого распределения энергии между модами.
Разница между соседними пространственными частотами |v p + 1 / — V p / | выбирается достаточно большой, чтобы коэффициенты в уравнении (9) могли быть представлены как:
Ф k + 1 ( x , У ) = arg F k + 1 ( x , y ) . (15)
Релаксационная способность итерационной процедуры может быть проконтролирована по уменьшению ошибки СКО:
PL PL
ZZ(Bp, — Cpk ISB2 pl p=0 l=0 JLp=0 l=0
C pl = J+J A ( x . У ) exp / Ф( x . У )] x (10)
x v pi ( x , У ) ехр [ / 2 n ( v ( p l x + v^ y ^xcly
В нашем случае процедура будет отличаться лишь специфическим выбором значений несущих:
Можно получить коэффициенты C pl с по-
'v pl = v p ' I ' p + I = p ' + 1 ' v pl * v pT p + l ^ p ' + 1 '
мощью двухмерного Фурье преобразования используя следующее уравнение [2]:
для мод Гаусса-Эрмита и
где
+^
F fc n) = J J A ( x , y ) • exP [ z ' ф( x , y )] x
—^
x Q ( x , y ) • exp [ z 2n ( ^ x + n y )] dxdy
'v pl =v p ' l ' 2 p + l = 2 p ' + 1' v pl * v p ' i ' 2 p + l * 2 p ' + 1 '
PL
Q ( x , y ) = EE v pi ( x , y ) (12)
p = 0 l = 0
для мод Гаусса-Лагерра.
3. Экспериментальные результаты
В данной работе производился итерационный расчет ДОЭ, формирующего из Гауссова пучка с распределением интенсивности
В fe n)
этом случае, функция
плоскости с координатами
p
в точках v^ ) бу-
I ( x , y ) = exp
V
2( x 2 + У 2)
2 ^ 0
дет равна передаточным коэффициентам:
F (^ = v p / « n = v ( p 2? ) = C pl (13)
В [2] для поиска фазы оптического элемента ф ( x,y ) был предложен следующий итерационный алгоритм. Выбирается начальная фаза ф 0 ( x, y ) .
Предположим, что на k итерационном шаге мы получаем фазу ф к ( X , y ) . Используя функцию
ф к ( X , y ) , мы получаем коэффициенты C ^k ) из
уравнения (13) или (10). Затем эти коэффициенты
несколько инвариантных модовых пакетов, распространяющихся вдоль оптической оси.
На Рис. 2 представлено трехмерное распределение интенсивности в выходной плоскости ДОЭ, формирующего четыре пакета мод Гаусса-Эрмита: rp j =1 - моды с порядковыми номерами (1,0),(0,1); rp r =2 - моды с номерами (2,0),(0,2),(1,1);
rp=3 - моды с номерами (3,0),(0,3),(2,1);
rp=4 - моды с номерами (4,0),(0,4),(3,1).
Ошибка формирования заданного распределения составляла 13% на десятой итерации, в то время как ошибка формирования четырех мод Гаусса-Эрмита элементом, рассчитанным процедурой [2], составила 23%. Таким образом, увеличение числа свободных параметров в зоне ди-
фракции Френеля с 4 до 13 привело к снижению ошибки в 1,8 раза.

Рис. 2.
На практике дальнейшее увеличение числа свободных параметров будет определятся, очевидно, числом каналируемых мод волновода (или числом отсечки [3]).
В [4] было показано, что Гауссовы моды не меняют своей структуры и при прохождении Фурье-каскада. В этом случае меняется лишь значение фундаментального радиуса моды σ на σ F , определяемое параметрами Фурье-каскада:
λf
σ F = . (20) σπ
На Рис. 3 и 4 приведены результаты моделирования прохождения модового пакета через Фурье-каскад. Рис.3 – амплитудное распределение суммы мод Гаусса-Эрмита с номерами (2,2) и (4,0) с единичными весами во входной плоскости Фурье-каскада, Рис.4 – в выходной.

Рис. 3.
Моделирование проводилось с помощью программного обеспечения "QUICK- DOE", разработанного в Институте систем обработки изображений РАН [5]. Необходимо отметить, что на практике приходится иметь дело с градиентными волокнами, реальный профиль которых значительно отличается от идеального параболического. Как правило, имеет место резкий провал значения показателя преломления в центре сердцевины волокна, что объясняется спецификой используемой технологии изготовления градиентных волокон.

Уменьшить влияние технологических погрешностей изготовления волокон можно, выбирая для передачи одного канала связи группу мод Гаус-са-Лагерра, связанных соотношением
2p+l = const, l ≠ 0 .
В данной работе проводился расчет и моделирование ДОЭ, формирующего 4 пакета мод Гаус-са-Лагерра со следующими значениями порядковых номеров:
rpl=15 - моды с номерами (5,5),(6,3),(7,1);
rpl=17 - моды с номерами (8,1),(6,5),(7,3);
rpl=19 - моды с номерами (9,1),(8,3),(7,5);
rpl=21 - моды с номерами (10,1),(9,3),(8,5).
Сумма квадратов коэффициентов при заданных модах в разложении комплексного распределения непосредственно за рассчитанным ДОЭ, составило 0,8. Таким образом, на формирование заданных мод приходится 80% энергии освещающего пучка.
На Рис. 5 и Рис. 6 представлены, соответственно, фаза ДОЭ, согласованного с пакетами мод Гаусса-Лагерра, и распределение амплитуды, сформированное ДОЭ в зоне дифракции Френеля.

Рис. 5.

Рис. 6.
Заключение
Разработан подход к повышению эффективности возбуждения мод градиентного волновода с помощью дифракционных оптических элементов в задачах уплотнения каналов волоконно-оптической связи, рассмотренных в [1]. Предложена модификация итерационного алгоритма [2], позволяющая существенно повысить эффективность формирования заданного модового состава и вместе с тем избежать уширения импульса, возникающего из-за межмодовой дисперсии [3], в каждом канале связи. Результаты вычислительных экспериментов демонстрируют весьма ощутимый выигрыш по сравнению с результатами, полученными при расчете ДОЭ алгоритмом [2]. В качестве возможной технологии изготовления ДОЭ, рассчитанного с помощью предлагаемой модификации процедуры [2], может быть выбрана технология многоуровневого травления резиста, описанная в [6].
На Рис. 7 представлена пятая бинарная маска из технологического комплекта масок, предназначенного для формирования 16-уровневого фазового рельефа ДОЭ, согласованного с пакетами мод Гаусса-Эрмита. Результат моделирования данного элемента приведен на Рис. 2. Комплект бинарных фотошаблонов для изготовления элемента был получен с помощью ПО
“DOE-tools”, разработанного в Институте систем обработки изображений РАН.

Рис.7.


