Эффективность алгоритма упреждающего обнаружения состояния передающего лазерного средства на основе приема и анализа нестационарного предгенерационного спонтанного излучения

Во многих случаях, часто встречающихся на практике, возникает острая необходимость обнаружения сигналов, исходящих от радиоэлектронных средств (РЭС), находящихся в процессе перехода из одного состояния (режима) в другое. Это обусловлено необходимостью качественного контроля исследуемых радиоэлектронных средств, дистанционного их мониторинга в группировках, радиоэлектронных средств, которые находятся в составе сложноиерархических систем. Как правило, излучения РЭС в переходных режимах до перехода в номинальный режим генерации сигнала представляет собой внеполосное и побочное излучение, характеризуемое явно выраженной нестационарностью. Все это в полной мере относится к передающим лазерным средствам, работающим в различных режимах и осуществляющим переход из некоторого исходного (выключенного) состояния в состояние генерации электромагнитного излучения с использованием различных способов модуляции добротности резонатора. Особенностью формирования излучений в лазерных средствах в ходе переходных процедур является наличие действий по накоплению энергии в активном элементе, а также его нагрев (при выходе на необходимый температурный уровень, а впоследствии и температурная стабилизация) при выходе на режим генерации, что порождает ИК-излучение активной среды, излучение системы оптической накачки, спонтан-– 511 – ное и спонтанно-индуцированное излучения, соответствующие различным энергетическим переходам активной среды, количество которых может быть значительным [1–5]. Наибольшей интенсивностью обладают чисто спонтанные и спонтанно-индуцированные излучения особенно в твердотельных лазерах с модуляцией добротности резонатора [6,7], а также подобные процессы аналогично проявляются и в волоконных лазерах с торцевой, с торцевой и одновременно боковой накачкой, с использованием полупроводниковых лазеров.

Повышение вероятности обнаружения спонтанного, спонтанно-индуцированного лазерного излучения возможно за счет использования в качестве полезного сигнала части спонтанно-индуцированного излучения, расположенного по времени ближе к моменту начала генерации основного излучения. Однако в ряде случаев возникает необходимость в более раннем обнаружении спонтанно-индуцированного излучения с тем, чтобы увеличить интервал времени от момента обнаружения до момента прихода (или генерации) основного излучения. Этот интервал можно рассматривать как располагаемое время, которое необходимо для подготовки и проведения определенных измерительных или других действий с использованием устройств, сопряженных с обнаружением указанных излучений [8–11]. Очевидно, что чем больше располагаемое время, тем более универсальным становится лазерный обнаружитель и тем более высокой устойчивости и эффективности можно достичь от сопрягаемых устройств, для которых лазерный обнаружитель выступает в качестве источника информации. Смещение процедуры обнаружения в более ранний период времени приводит к тому, что рассматриваемый полезный сигнал (спонтанное излучение) становится заметно слабее, что приводит к необходимости увеличения длительности интервала накопления сигнала в приемнике лазерного обнаружителя. В свою очередь, увеличение длительности интервала накопления в некоторой степени сокращает располагаемое время, что может негативно сказаться на эффективности функционирования сопрягаемого с лазерным обнаружителем устройства.

Исходя из вышесказанного, целью данной работы является разработка алгоритма устойчивого обнаружения спонтанного излучения с заданными условными вероятностями правильного обнаружения и ложной тревоги, обеспечивающего при этом максимальное значение длительности располагаемого времени.

Для достижения указанной цели вначале рассмотрим задачу обнаружения спонтанного излучения как нестационарного сигнала с формой, отражающей его амплитудное увеличение, и с процедурой его накопления в приемном устройстве при произвольном выборе момента начала процесса накопления.

Обоснование формы и основных характеристик предгенерационных спонтанных излучений лазерных средств

В ходе экспериментальных и теоретических исследований [5, 6, 12] по определению характеристик предгенерационных лазерных каналов основное внимание было сосредоточено на спонтанных излучениях, излучении накачки и ИК-излучениях оптических элементов передающего лазерного средства. При этом полученные количественные результаты представлялись в виде характерных энергетических, пространственно-временных и амплитудновременных параметров.

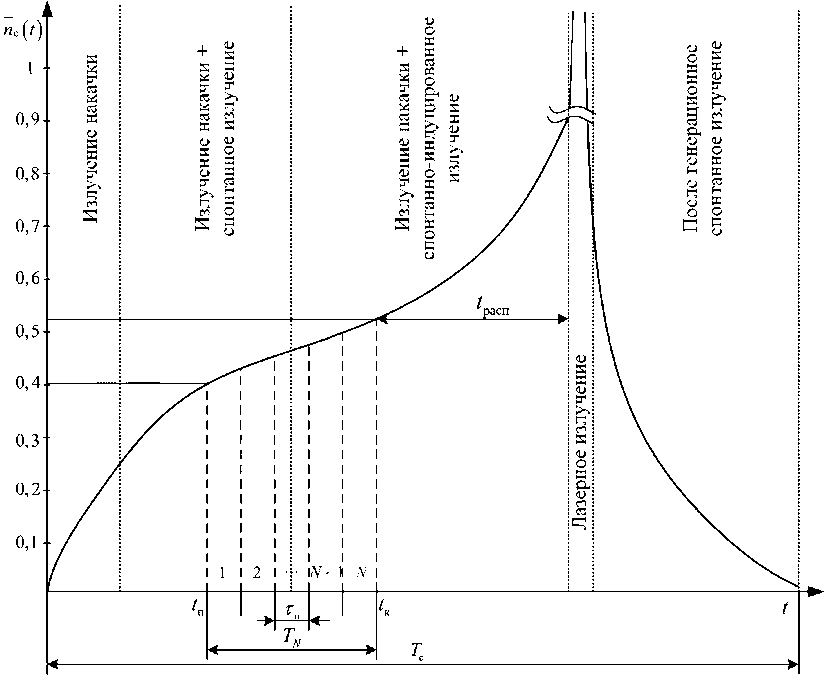
Рис. 1. Динамика формирования предгенерационного и послегенерационных излучений лазерного средства с модуляцией добротности, в том числе на фоне интервала наблюдения длительностью T N .

Fig. 1. Dynamics of formation of pre-generation and post-generation radiation of a Q-modulated laser device, including against the background of an observation interval of duration T _N

Так на рис. 1 представлен типовой, показательный график зависимостей интенсивности излучения на выходе передающего лазерного канала, работающего в режиме модуляции добротности резонатора, когда в качестве модуляторов используются электрооптические системы.

Форма такого сложного сигнала (излучения) может считаться частично известной. Однако если период наблюдения T N <<  T c (где T c – полная длительность излучения), то в связи с неопределенностью выбора моментов времени начала и завершения наблюдения (части такого составного сигнала) форма принимаемого сигнала будет в общем случае неизвестной. Можно предположить, что с использованием информации об основном генерируемом сигнале (гигантском импульсе) рассматриваемое излучение до появления основного сигнала будет нарастающим, а по завершении генерации будет спадающим. Кроме того, предгенерационное и послеге-нерационное спонтанные излучения имеют достаточно выраженный дискретный оптический спектр, составляющие которого по-разному изменяют свои амплитудные характеристики во времени. При избирательном приеме и анализе составляющие такого спектра в общем случае будут неизвестными, так как для случая предгенерационных излучений некоторые оптические составляющие спектра в течение этого периода могут как увеличивать свои амплитудные характеристики до определенной величины, так и уменьшать их в момент, когда начинают доминировать спонтанно-индуцированные переходы [12, 13].

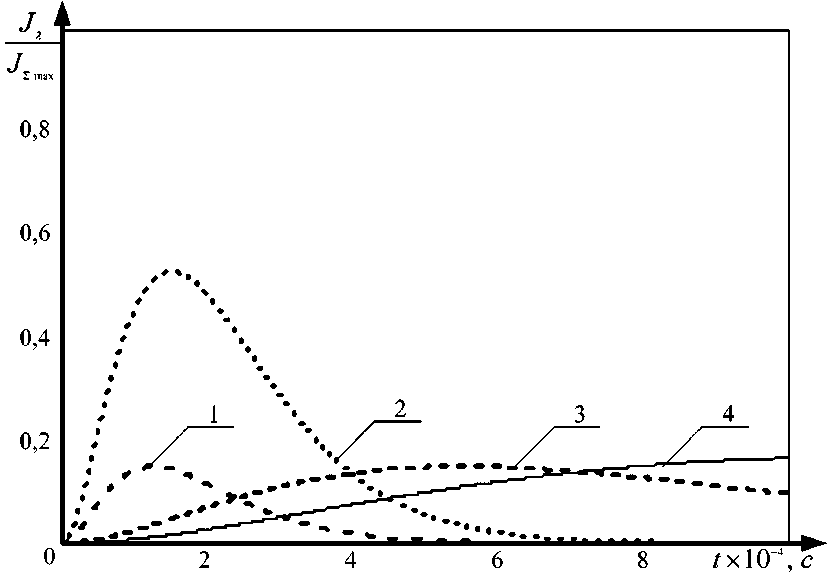
Рис. 2. Временное распределение спонтанного излучения в зависимости от длины волны: 1 – для перехода с λ=0,91 мкм; 2 – для основного лазерного перехода с λ=1,06 мкм; 3 – для перехода с λ=1,34 мкм; 4 – для перехода с λ=1,9 мкм

Fig. 2. Temporal distribution of spontaneous emission depending on the wavelength: 1 – for the transition with λ=0,91 μm; 2 – for the main laser transition with λ=1,06 μm; 3 – for the transition with λ=1,34 μm; 4 – for the transition with λ=1,9 μm

На рис. 2 представлены амплитудно-временные (с учетом усредненных значений вероятности выбора нижнего энергетического уровня при спонтанном излучении) зависимости спонтанных излучений на длинах волн 0,91 мкм, 1,06 мкм, 1,34 мкм и 1,9 мкм от относительного значения времени ( t / t _п, где t _п – время достижений пикового значения мощности, рассеиваемой в лампе накачки) [5].

Для представленных на рис. 2 результатов предгенерационные спонтанные излучения соответствуют интервалу от начала координат до момента времени, когда зависимость 2, описывающая интенсивность излучения на основной длине волны (λ=1,06 мкм), примет максимальное значение (момент времени включения модулятора добротности).

Следует отметить, что полученные амплитудно-временные зависимости излучения на выходе передающего канала получены при неполном резонаторе, когда модулятор добротности находится в состоянии постоянного обеспечения минимального значения коэффициента отражения. В этом случае предгенерационные спонтанные излучения будут формироваться до момента времени достижения интенсивностей максимального значения, что соответствует моменту включения модулятора добротности резонатора.

По итогам обобщения и анализа результатов исследования характеристик и параметров спонтанных, спонтанно-индуцированных излучений можно сделать вывод.

• 1.    Амплитудно-временная зависимость рассматриваемых излучений, от момента накачки до момента генерации основного излучения, имеет возрастающий характер с явно выраженной нелинейностью на этапе формирования спонтанно-индуцированного излучения.

• 2.    Предгенерационное спонтанное излучение может быть условно разделено на два излучения – чисто спонтанное излучение и спонтанно-индуцированное излучение.

• 3.    С увеличением плотности инверсной населенности происходит изменение роста абсолютных значений спонтанных излучений из-за различных ускорений изменений, связанных с одновременным влиянием коэффициентов Эйнштейна для вынужденных переходов и значений вероятностей спонтанных переходов между уровнями в единицу времени.

• 4.    Абсолютные значения интенсивностей спонтанных излучений обеспечивают устойчивое их обнаружение в типовых условиях фонового излучения на дальностях, в некоторых случаях, превышающих дальность действия исследуемых лазерных средств [5].

Алгоритм обнаружения спонтанного предгенерационного излучения

Применительно к ситуации, представленной на рис. 1, отражающей общую форму сигнала и расположение выделенной наблюдаемой «посылки» T N , которая разбита на N подынтервалов одинаковой длительностью τ _н. Поступая аналогично [14, 15], будем считать, что в течение длительности подынтервала τ _н наблюдается возрастающее по интенсивности (фотоэлектронов/ секунду) обнаруживаемое излучение, так что интенсивность излучения в i -ом подынтервале запишется в виде γ_ci, где i = 1,2,…, N. При этом шумовая помеха предполагается стационарной с постоянной интенсивностью γ_шi = γ_ш для всех i = 1,2,…, N

Приемник анализирует реализацию на интервале [ t _н; t _к] длительностью T _{N 0}, где t _н, t _к – начальный и конечный момент времени анализа (накопления) соответственно. При этом после каждого интервала длительностью τ н «берется» отсчет. В связи с этим число отсчетов в выборке равно N . Величина отсчетов в выборке равна числу фотоэлектронов, подсчитываемых приемником в течение длительности τ _н. Решение принимается после последовательного накопления всех N отсчетов [16].

Предположим, что отсчеты в подынтервалах статистически независимы, а решая задачу обнаружения, будем считать, что сигнал слабый и, следовательно, подчинен пуассоновской статистике. Также будем считать, что приемник работает по правилу Неймана–Пирсона с квантовым счетчиком в качестве чувствительного элемента.

С учетом изложенного имеющаяся на входе приемника выборка из реализации n ₁, n ₂,…, n _i,…, n _N отожествляется с наличием сигнала в том случае, если выполняется неравенство [14, 15],

A^n_l,n₂,..,n_j,..,n_N^ = —у---------------у > 2₀                          (1)

или отождествляется с наличием лишь шума, если λ <  λ ₀, где P ₁ – совместная плотность вероятности для совокупности выборочных значений n ₁, n ₂,…, n _i,…, n _N при условии, что сигнал присутствует; P 0 – совместная плотность вероятности для той же совокупности выборочных значений при условии, что сигнала нет; λ ₀ – пороговая величина, которая выбирается из условия выполнения неравенства λ ≥ λ ₀ при отсутствии сигнала и фиксированном значении условной вероятности ложных тревог P _лт.

Процесс отождествления выборки удобно увязать с гипотезами, гипотеза H ₀ соответствует случаю, когда на вход приемника поступает лишь помеховое излучение, а гипотеза H ₁ соответствует случаю, когда на вход приемника поступает аддитивная смесь полезного (обнаруживаемого) сигнала и помехи.

Для сделанного предположения, что выборочные значения статистически независимы, выражение можно представит в виде:

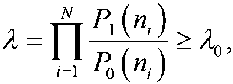
где P 1 ( n i ) и P 0 ( n i ) – плотности вероятности i -ых выборочных значений соответственно при наличии и отсутствии сигнала. Следовательно, при λ ≥ λ 0 принимается гипотеза H ₁, в противном случае гипотеза H ₀.

Введем в рассмотрение среднее число сигнальных фотоэлектронов за время i -го отсчета ( S _a ) и среднее число шумовых фотоэлектронов за время i -го отсчёта ( S ш), определив их как:

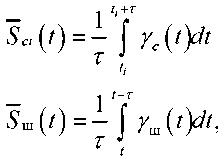
где γ ci – интенсивности потока сигнальных фотоэлектронов в выборке; γ ш – интенсивности i потока шумовых фотоэлектронов в выборках (γ шi = γ ш ).

Тогда с учетом и сделанных предположений можем записать, что

(Sci+S^ _ _

РДи.)^      7 ,е-(мш)                                   (4)

ЛА) = ^Ц-е'ш-                                    (5)

Подставляя и в получим:

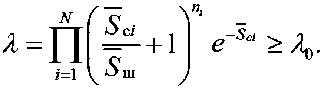
Логарифмируя и вводя обозначения Λ = ln λ находим:

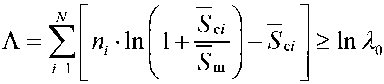
Выражение позволяет представить структуру оптимального приемника-обнаружителя спонтанного излучения лазерного средства в виде, представленном на рис. 3.

Оптимальный приемник последовательного накапливает все взвешенные отсчеты, при этом коэффициент взвешивания для каждого отсчета свой и определяется разностью 111 ^ S in + S ci j 111 S in , после чего на основании сравнения с пороговым значением принимается решение о наличии или отсутствии спонтанного излучения в принятом сигнале. Величина порога может быть предварительно оценена из выражения ln2 + ^5„.

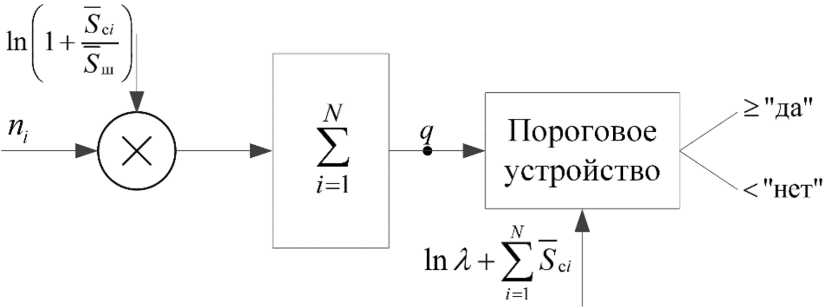
Рис. 3. Оптимальная схема приемника обнаружителя нестационарного спонтанного излучения передающего канала лазерного средства с последовательным накоплением импульсов

Fig. 3. Optimal circuit of the receiver of the detector of non-stationary spontaneous radiation of the transmitting channel of a laser device with sequential accumulation of pulses

Оценка эффективности алгоритма

Для исследования на эффективность алгоритма обнаружения, структура которого представлена на рис. 3, определим статистику сигнала в точке q (рис. 3). Введем в рассмотрение ве-

N       _ _ личину ^ = ^ И, ■ In (1 + Sc,/Sin ). Будем полагать, что значение q в силу центральной предельной

Z=1

теоремы «нормализуется» в одноименной обозначенной точке как взвешенный накопленный сигнал для последующего выбора гипотез H 1 (есть обнаруживаемый сигнал) или гипотезы H 0 (нет обнаруживаемого сигнала). Тогда для гипотезы H ₁ среднее значение рассматриваемого сигнала в точке q .

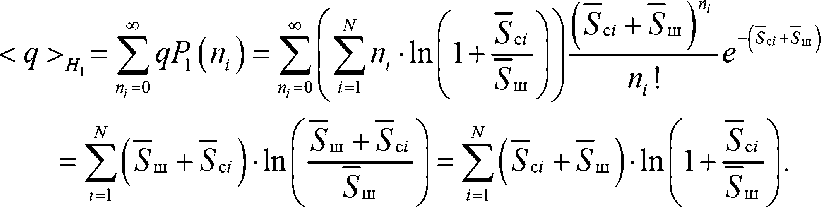
Дисперсию определим как сумму дисперсий каждого отсчета, которая для одного отсчета определяется как

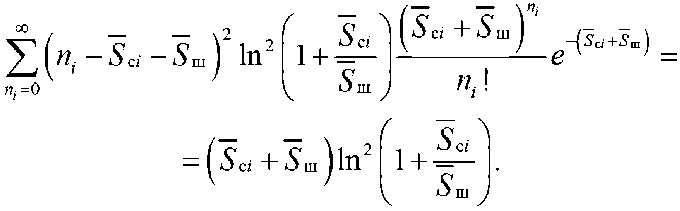
Тогда дисперсия последовательно накопленного сигнала (применительно к точке q )

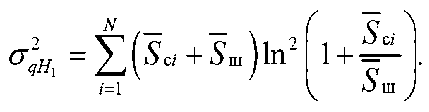
Среднее значение и дисперсия последовательного накопленного сигнала применительно к гипотезе H ₀ будет определяться с помощью следующих выражений.

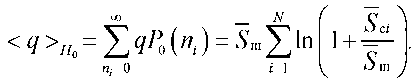
qh0

N —      VI

= рш1п2 1 + ^ .

Введем в рассмотрение плотности вероятности величин амплитуд сигналов, в точке q при гипотезе H 0 и H 1 в виде:

/ЙМ) =

1 e ^2a^° ,

2/F ^"

/W)^- e ²^ .

С использованием выражений и можем записать аналитическое выражение для оценки условных вероятностей правильного обнаружения и наступления ложной тревоги при наблюдении приемником входного воздействия в течение интервала времени T N .

Подставим в и зна

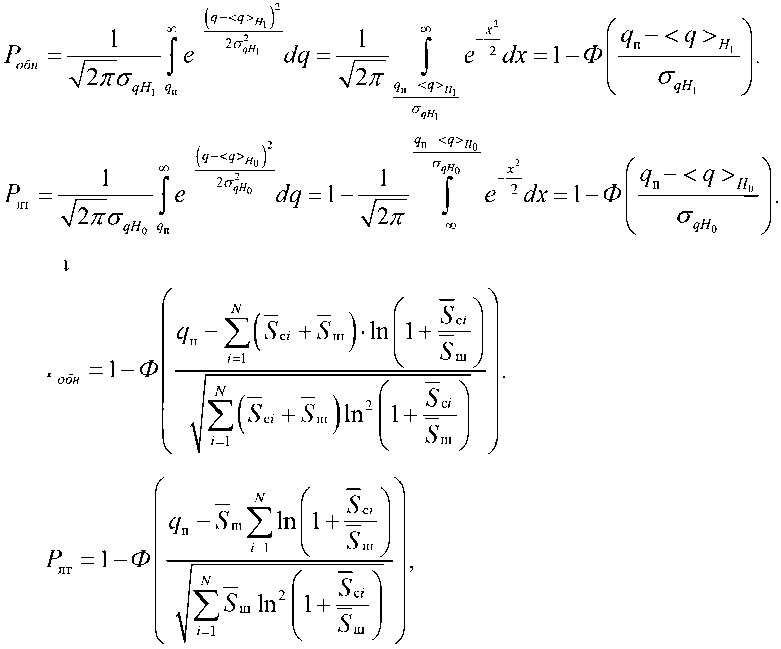
В свою очередь, используя, предполагая реализацию критерия Неймана-Пирсона, можем записать равенство для величины порога.

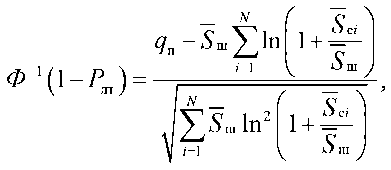
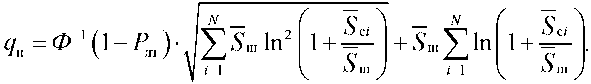
где Ф ^-1[ Ф ( x )] = x – обратная функция.

Подставим в, находим

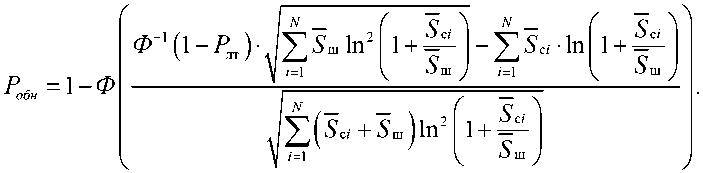
Выражение позволяет оценить эффективность оптического приемника, реализующего алгоритм обнаружения, изображенный схематично на рис. 3. В качестве показателя эффективности используется условная вероятность правильного обнаружения, представленная как зависимость от числа фотоотсчетов, обусловленных воздействием на вход приемника полезного и помехового (шумового) сигналов, а также от длительности интервала наблюдения (числа отсчетов) и от момента времени начала осуществления наблюдения в интервале времени формирования разведывательного передающим средствам предгенерационного спонтанного и спонтанно-индуцированного излучений [17].

Линеаризация зависимости интенсивности от времени спонтанной генерации

Перейдем к рассмотрению интенсивности спонтанного-индуцированного излучения, которое воздействует на вход оптического приемника, анализирующего его с момента времени t _н, накапливая сигнал до момента времени t _к (рис. 1), после чего с учетом шума формируется решение о наличии или отсутствии полезного сигнала. На практике длительность подынтервала τ _н весьма малая величина (~10^–8c) по сравнению с длительностью спонтанного излучения на выходе лазерного средства, работающего в режиме модуляции добротности резонатора (~10^–4c). Это позволяет приемлемо использовать метод линеаризации (рис. 4) на интервалах 10^–6c – 10^–5c с приемлемым качеством [18, 19].

Число подынтервалов с длительностью τ н может составлять в этом случае N = 10²–10³. Что подтверждает возможность одновременного взвешенного накопления входного воздействия с использованием основных результатов и выводов центральной предельной теоремы для последовательностей независимых случайных величин [20, 21], а также линеаризации. Для реализации процедуры линеаризации воспользуемся выражением:

_7c(t) = kt + b,                                                              (22)

где k и b – угловой коэффициент и начальная ордината, соответственно, определяемые из выражений k=tga=r^kzM^ Ь^УК,               (23)

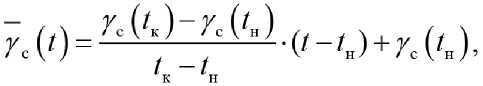
где t н ≤ t ≤ t к .

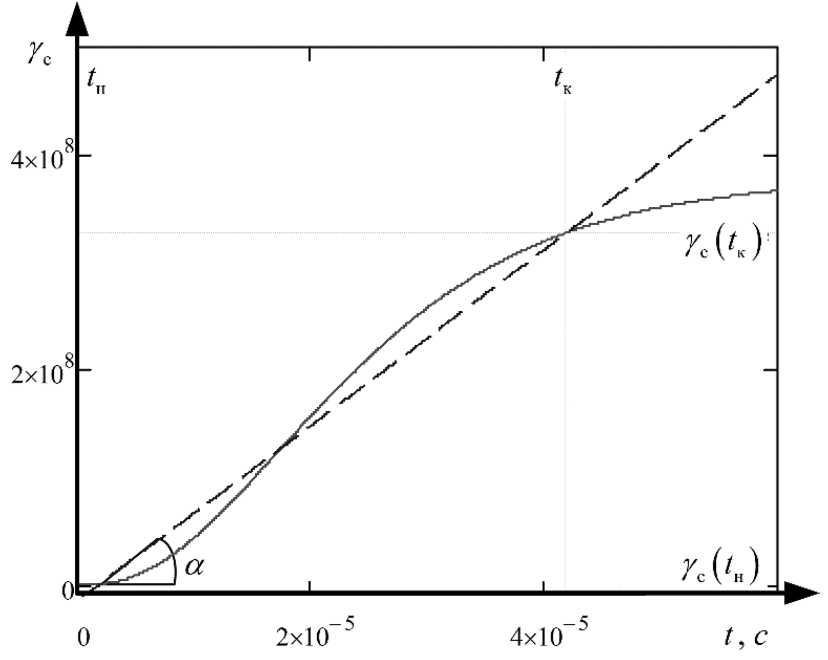
Рис. 4. Использование метода линеаризации

Fig. 4. Using the linearization method

Тогда среднее число сигнальных фотоэлектронов (образования переходов) может быть определено из выражения:

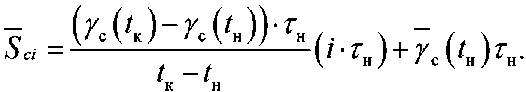
где ( t н = i · τ н ) ≤ t к – t н .

В свою очередь, использование (25) позволяет осуществить замену операции суммирования на интегрирования [22–24], которая преобразует выражение к виду:

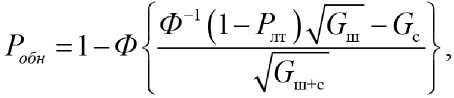
на интервале t н ≤ t ≤ t к , при принятых обозначениях:

г=1              Ош у х(4(фп2^к)-2д(?к)Ь^к) + 24(/к)-д(?н)Ь2^н) + 24(/н)М^^     ; (28)

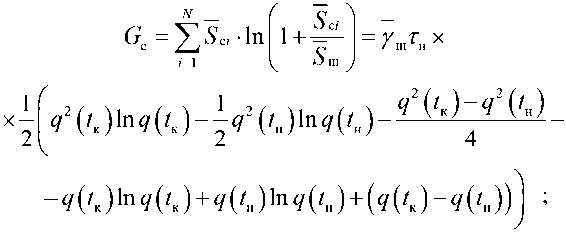
В свою очередь,

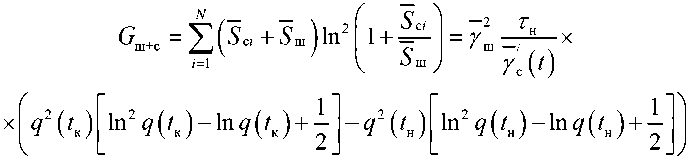
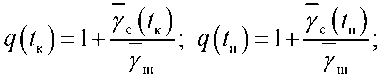
где t н ≤ t ≤ t к .

Оценка влияния линеаризации на вероятность обнаружения предгенерационного излучения

В целях оценки влияния линеаризации на обнаружения предгенерационного излучения с использованием выражений –, основанных на экспериментальных значениях интенсивности потока сигнальных фотоэлектронов, приведенных в табл. 1, произведено моделирование изменения зависимости вероятности правильного обнаружения от длительности интервала наблюдения (линеаризации) T , числа подынтервалов наблюдения i = 1,2,…, N и начального момента наблюдения t н .

Таблица 1. Интенсивность потока сигнальных фотоэлектронов

Table 1 Intensity of the signal photoelectron flux

Интенсивность потока сигнальных фотоэлектронов γ c ( t )×10–8, 1/c	Момент времени, относительно начала накачки, мкс
	1	10	15	20	25	30	35	40	45	50	55	60	65
	5 · 10–3	0,05	0,26	0,58	0,94	1,27	1,54	1,76	1,91	2,03	2,11	2,16	2,19

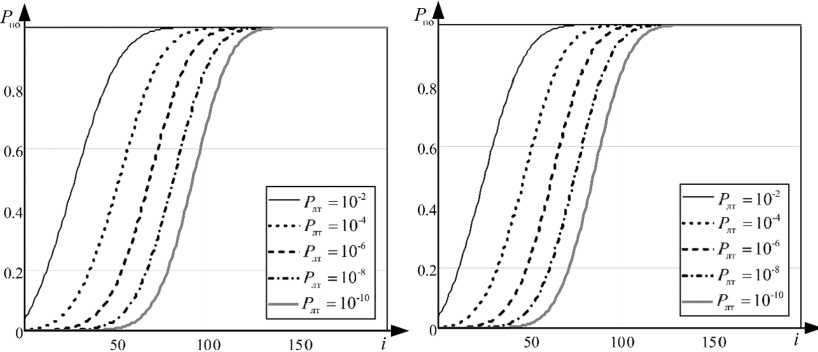
На рис. 5 представлены зависимости вероятности правильного обнаружения от числа подынтервалов наблюдения i для различных типовых значений условной вероятности ложных тревог. Графики получены при следующих исходных данных: интенсивность потока шумовых фотоэлектронов γ_ш( t ) = 10⁸ 1/c, длительность подынтервала наблюдения τ_н = 5 × 10⁸ c, момент начала наблюдения (с момента начала накачки) t н = 8 × 10^–6 c, интервал наблюдения изменялся в диапазоне T _N = (5 ÷ 20) × 10^–6 с.

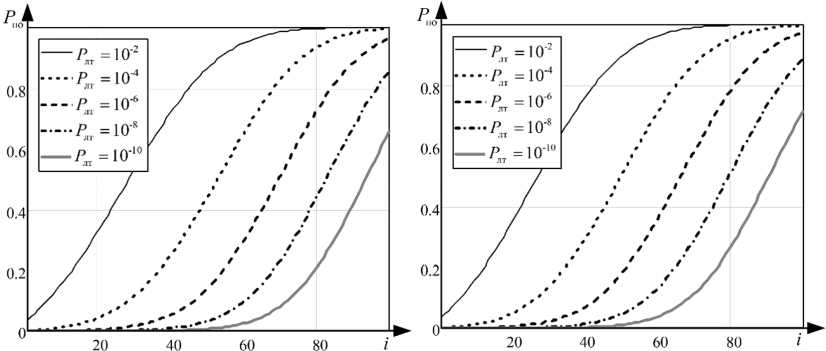
( T N = 5 × 10^–6 c, N = 100)

d)

c)

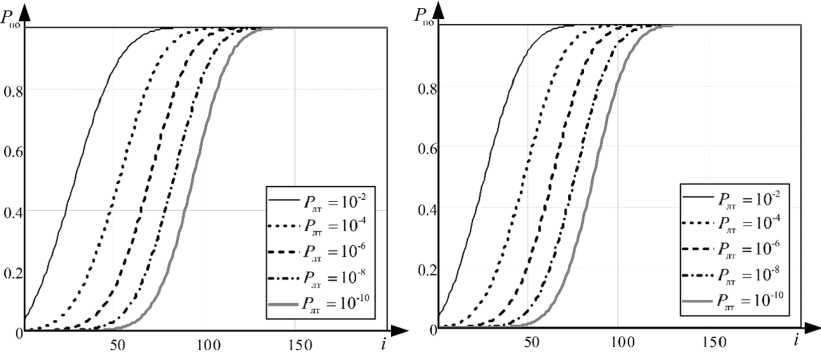
( T N = 10 × 10^–6 c, N = 200)

• e)                                                                  f)

( T N = 20 × 10^–6 c, N = 400)

Рис. 5. Зависимость вероятности правильного обнаружения от подынтервала наблюдения i для линеаризованного (a, b, c) и исходного значений (d, e, f) интенсивности излучения

Fig. 5. Dependence of the probability of correct detection on the observation subinterval i for the linearized (a, b, c) and initial values (d, e, f) of the radiation intensity

Анализ графиков показывает наличие расхождения в вероятностях обнаружения для исходного и линеаризованного потока фотоэлектронов, изменяющегося с ростом периода наблюдения.

На рис. 6 приведены графические зависимости вероятностей правильного обнаружения для исходных и линеаризованных значений, а также абсолютное значение ошибки в оценке вероятности Δ P для случая, когда: P _лт = 10^–8, τ _н = 5 · 10^–8 с, а интервал наблюдения (интервал линеаризации) принимается равными: T N = 5 × 10^–6 c (рис. 6 a) и T N = 20 × 10^–6 c (рис. 6 b).

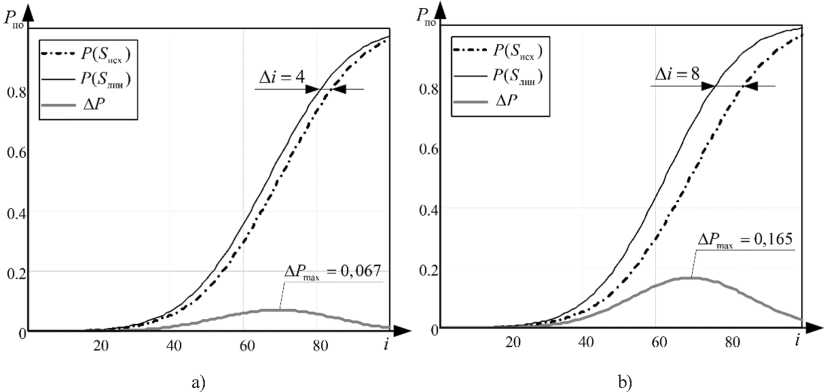
Рис. 6. Зависимость расхождения в вероятностях обнаружения от числа подынтервалов наблюдения i

Fig. 6. Dependence of the discrepancy in detection probabilities on the number of observation subintervals i

Из графиков, приведенных на рис. 6, видно расхождение в вероятностях обнаружения вследствие линеаризации, возрастающее с ростом интервала наблюдения. Причиной данного эффекта является начало наблюдения ( t н = 8 × 10^–6 c) в момент нелинейного роста интенсивности спонтанного излучения, из чего следует необходимость исследования влияния выбора начального момента наблюдения на величину ошибки линеаризации.

Исследования показали возможность снижения расхождения в определении величин вероятности обнаружения до значений менее единиц процентов, при смешении начало наблюдения к более позднему моменту времени, в зону более линейного роста интенсивности излучения ( t _н = 20 × 10^–6 c). Однако данное решение привело к смещению располагаемого времени до момента генерации основного лазерного излучения в область значений порядка (1 ÷ 2) × 10^–5 с. При этом устойчивое обнаружение будет осуществляться уже на i = 17 подынтервале наблюдения, следовательно, последующие такты наблюдения будут избыточными.

В результате исследования влияния момента начала наблюдения на потребное количество подынтервалов i _обн, обеспечивающих устойчивое обнаружение предгенерационного излучения, были получены графические зависимости, приведенные на рис. 7. В качестве потребного количества подынтервалов наблюдения принималось значение, удовлетворяющее условию:

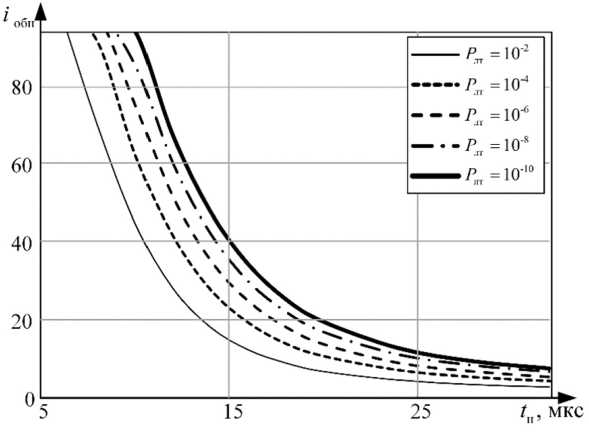
Рис. 7. Зависимость количество подынтервалов наблюдения, обеспечивающих устойчивое обнаружение

Fig. 7. Dependence of the number of observation subintervals that ensure stable detection

?’обн = argminPA(zo6H), (32)

где P Δ ( i обн ) = ǀ P по ( i обн ) – P уст ǀ, P уст = 0,99 – вероятности устойчивого обнаружения – принятое в качестве целевого значение вероятности правильного обнаружения.

Полагая интервал времени между началом накачки и моментом генерации основного излучения равным 6 × 10–5 c, с учетом ранее полученного потребного количества подынтервалов наблюдения, обеспечивающих достаточную вероятность правильного обнаружения, получены графические зависимости располагаемого времени от начального момента наблюдения, приведенные на рис. 8.

Результаты анализа графиков, приведенных на рис. 5–7, свидетельствуют о возможности практического применения допущения о линейности зависимости интенсивности от времени спонтанной генерации при определенных ограничениях, выражающихся в существенных расхождениях с исходными значениями в начальные моменты ( t н < 10 × 10^–6 c) спонтанной гене-

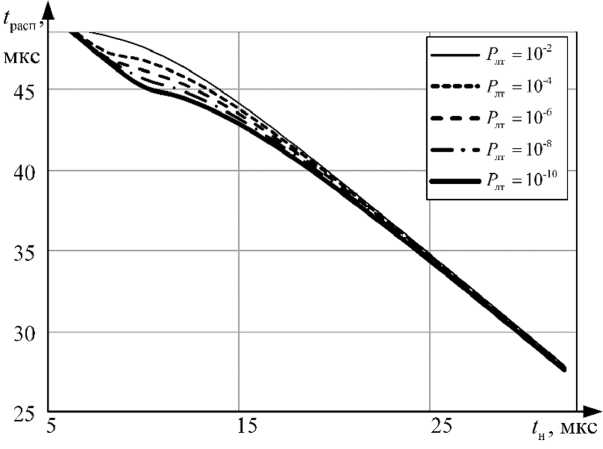
Рис. 8. Зависимость располагаемого времени от момента начала наблюдения

Fig .8. Dependence of available time on the moment of observation start рации, отличающиеся большой нелинейностью, что может быть компенсировано задержкой начала наблюдения. Уменьшение располагаемого времени вследствие смещения начального момента наблюдения может быть частично нивелировано рациональным выбором числа подынтервалов наблюдения, обеспечивающего потребную вероятность правильного обнаружения.

Заключение

Таким образом, можно сделать следующие выводы.

• 1.    При использовании в качестве демаскирующего признака функционирования и определения состояния передающих лазерных каналов предгенерационного спонтанного излучения возможно обнаружение передающего лазерного канала на дальностях, превышающих дальности работы самих обнаруживаемых лазерных средств. При этом устойчивое обнаружение ( P обн = 0,99) осуществляется с упреждением по отношению к зондирующему импульсу, формируемому этим передающим каналом на время t расп (3 ÷ 5) × 10^–5 с, что может считаться достаточным для реализации ряда мероприятий, в том числе и для реализации защитных мер.

• 2.    Рациональный выбор начала и длительности наблюдения должен осуществляться исходя из конкретики предназначения информационного обеспечения с учетом необходимого значения длительности располагаемого времени и возникающих ограничений на длительность наблюдения (особенно в условиях конфликта).

• 3.    Обоснование рационального алгоритма обнаружения оптическим приемником нестационарного спонтанного излучения осуществлялось в пуассоновских шумах, имеющих стационарный характер. Оценка эффективности алгоритма осуществлялась с учетом наличия процесса взвешенного суммирования принимаемого входного сигнала в исследуемом алгоритме, что дало возможность применить основные рекомендации, следующие из центральной предельной теоремы для последовательностей независимых случайных величин, что позволило провести оценки основных характеристик (среднего и дисперсии) суммированного взвешенного сигнала с выхода сумматора и привести функцию распределения к нормальной.