Эффективность использования идеологии мастер-процесса при параллельной реализации итерационных процедур решения линейных систем

Развитие аппаратных мощностей вычислительных систем и численных методик решения сложных задач обусловили широкое применение ЭВМ в различных областях науки и техники. Зачастую для получения результатов решения с высокой точностью программные реализации алгоритмов решения задачи предъявляют повышенные требования к вычислительным ресурсам, соответственно, время получения решения оказывается неприемлемо велико. Применение многопроцессорных систем и параллельных вычислительных технологий существенно расширяет возможности исследователей, занимающихся численными экспериментами.

Достаточно часто при численном анализе краевых задач возникает необходимость решения системы линейных алгебраических уравнений (СЛАУ) большой размерности, которая может быть представлена в виде

[ A ]{х} { b}, (1)

где [ A ] - матрица коэффициентов системы; { 6 } - вектор правой части; { х } - вектор неизвестных.

При получении решения системы линейных алгебраических уравнений наиболее эффективно работают алгоритмы, построенные по принципу параллельной обработки данных в рамках различных процессов, когда длительные математические операции над матрицами и векторами производятся одновременно несколькими независимыми процессами. Данный способ позволяет эффективно использовать в программе как многопроцессорные (кластерные) системы, так и современные многоядерные процессоры.

Эффективность применения параллельных вычислений подтверждена большим числом работ на данную тему. В работе [1] рассматривается параллельная реализация метода квадратного корня при нахождении решения системы алгебраических уравнений, полученной в ходе реализации метода граничных элементов. Работы [2] и [3] посвящены аспектам построения параллельной реализации итерационных методов решения систем линейных алгебраических уравнений. Как отмечается в [4], построение эффективного параллельного алгоритма представляет собой сложную задачу и автор прибегает к готовым библиотекам параллельных алгоритмов. Основным минусом данного подхода является отсутствие учета особенностей исследуемой задачи. Как правило, все реализации предполагают сборку матрицы коэффициентов системы в рамках одного процесса с последующей рассылкой ее блоков по рабочим процессам системы. При этом разделение производится построчно.

На сегодняшний день при решении СЛАУ большой размерности большее распространение получили итерационные методы. К их преимуществам следует отнести существенно меньшее накопление погрешности при получении решения, высокую эффективность выполнения матричных операций при использовании разреженных форматов хранения матрицы коэффициентов, возможность более быстрого получения начальных приближений искомого решения, наличие эффективных способов организации параллельных вычислений. Дополнительно следует упомянуть неизменность структуры матрицы коэффициентов, что существенно при использовании разреженных форматов хранения.

В настоящее время используются два подхода в организации архитектуры параллельных вычислительных программных средств: с использованием и без использования мастер-процесса, функции которого заключаются в координировании работы остальных вычислительных процессов системы. Целью данного исследования является анализ эффективности применения идеологии мастер-процесса при построении параллельных алгоритмов методов сопряженных градиентов и Якоби.

В данной работе рассматриваются две архитектуры параллельных вычислительных систем. Первый подход подразумевает наличие мастер-процесса, совершающего все векторные операции, при этом параллельный алгоритм строится только для нахождения произведения матрицы коэффициентов на вектор. Основное преимущество данного подхода заключается в минимизации количества операций передачи данных между параллельными потоками вычислений. Операции передачи данных производятся значительно медленнее операций вычисления, таким образом, данный подход позволит существенно сократить издержки синхронизации процессов.

Второй подход подразумевает отсутствие мастер-процесса, все математические операции на каждой итерации методов решения СЛАУ производятся децентрализованно. Повышение количества передаваемых данных компенсируется снижением количества последовательных вычислений в рамках каждого процесса.

1.    Применение параллельных вычислений при выполнении основных операций

Для построения параллельного алгоритма умножения матрицы коэффициентов на вектор предлагается разделить матрицу коэффициентов по строкам на p блоков, где p соответствует числу параллельных вычислительных процессов. Вектор, на который производится умножение, передается всем процессам. Для обеспечения равномерности нагрузки на параллельно выполняющиеся ветви алгоритма рекомендуется определить равное число строк для каждого блока. В результате произведения каждый процесс определяет свой блок элементов результирующего вектора (рис. 1).

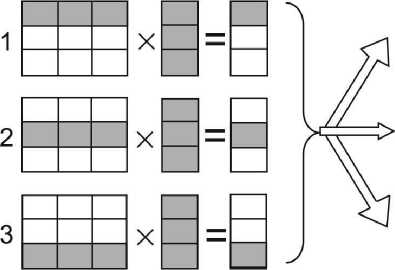
Рис. 1. Схема параллельного умножения матрицы на вектор

Для реализации математических операций над векторами предлагается разделение векторов на блоки с закреплением каждого блока за конкретным процессом. Таким образом, операции сложения и вычитания векторов будут производиться одновременно над несколькими блоками; результат данных операций будет сразу представлен в виде, предназначенном для параллельного алгоритма (рис. 2, а ). Аналогично предлагается строить операцию умножения вектора на скаляр (рис. 2, б) . Для получения результатов операции перемножения векторов потребуется также провести коллективную операцию передачи данных с суммированием (рис. 3). После проведения данной операции каждый процесс получает свою копию вектора результата.

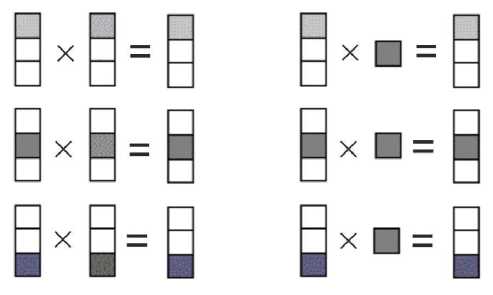
а                            б

Рис. 2. Скалярные операции над векторами: а - сложение векторов; б - умножение вектора на скаляр

В случае применения первого подхода требуется выполнение процедуры сборки данных и получение полного результирующего вектора в рамках мастер-процесса. В случае применения второй методики объединение данных не требуется.

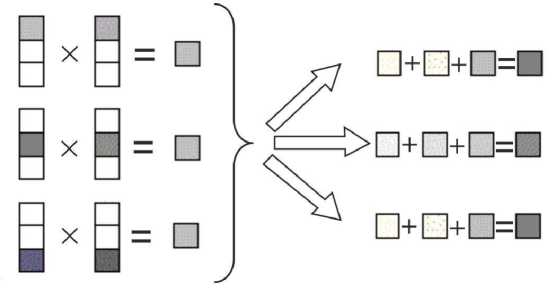
Рис. 3. Схема параллельного алгоритма произведения векторов

Численные эксперименты проводились применительно к системе линейных алгебраических уравнений, полученной при реализации метода конечных элементов для двумерной задачи. В силу разреженности матрицы коэффициентов системы использовалась строчная схема хранения RR(C)U [5], применение которой позволяет существенно повысить эффективность операции произведения матрицы на вектор.

Реализация параллельного алгоритма была построена на основе интерфейса передачи сообщений между процессами MPI (Message Passing Interface) [6]. Данный инструмент позволяет использовать программный продукт на различных аппаратных архитектурах, не требуя дополнительного изменения алгоритма и его реализации.

Численный эксперимент был поставлен на ЭВМ класса «персональный компьютер», работающей под управлением шестиядерного процессора AMD® Phenom II X6 1075T. Программная реализация итерационных алгоритмов решения системы линейных алгебраических уравнений была произведена на языке программирования C#. Для обеспечения взаимодействия параллельных процессов использовался стандарт MPI 2.0.

В качестве критерия количественного анализа в соответствии с [7] использовалось «ускорение», равное отношению времени выполнения последовательного алгоритма ко времени выполнения параллельного алгоритма.

2.    Применение метода сопряженных градиентов

Метод сопряженных градиентов - итерационный метод для безусловной оптимизации в многомерном пространстве [8]. Основное достоинство метода заключается в достижении точного решения при обработке систем с положительно определенной матрицей коэффициентов за конечное число итераций.

Схема данного метода (рис. 4) подразумевает выполнение на каждой итерации одной операции произведения матрицы на вектор и девяти скалярных операций над векторами.

Рис. 4. Схема метода сопряженных градиентов

На рис. 5, 6 представлены зависимости ускорения от числа параллельных процессов при решении систем различной размерности. Рассматриваются варианты построения параллельного алгоритма без главного процесса и с главным процессом соответственно. Увеличение длительности работы параллельных алгоритмов для СЛАУ малой размерности объясняется тем, что трудоемкость обмена данными между процессорами больше, чем вычислительная трудоемкость частей задачи, выполняемых в рамках разных процессов. Построение параллель- ного алгоритма, производящего математические операции над векторами, позволяет получить более высокие коэффициенты ускорения.

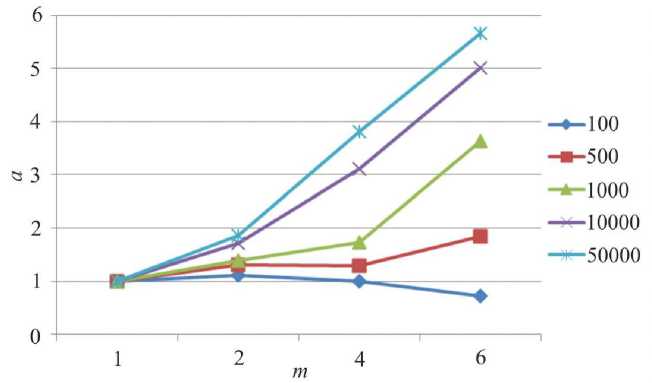
Рис. 5. Зависимость ускорения а параллельного алгоритма от числа процессоров m для сеток разной размерности в параллельной модели без мастер-процесса

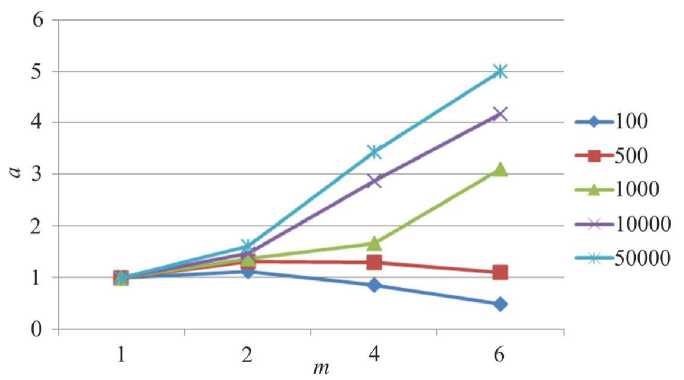
Рис. 6. Зависимость ускорения а параллельного алгоритма от числа процессоров m для сеток разной размерности в параллельной модели, содержащей мастер-процесс

3.    Применение метода Якоби

Схема данного метода [9] (рис. 7) подразумевает выполнение на каждой итерации одной операции произведения матрицы на вектор и двух скалярных операций над векторами. Метод Якоби требует предварительного представления матрицы коэффициентов уравнения (1) в следующем виде:

[ A ]=[ D ]+[ L ]+[и ],

где [ D ] - диагональная матрица; [ ^ ] и [ L ] - верхняя и нижняя треугольные матрицы с нулевыми главными диагоналями. Итерационная схема метода имеет вид

{х} k+1 =[ B ]{ х} k +{g }, где [B] = [DГ1 ([L] + [U]), {g} = [D]"1 {b}.

При анализе результатов время, необходимое на построение [ B ] и { g }, не учитывалось.

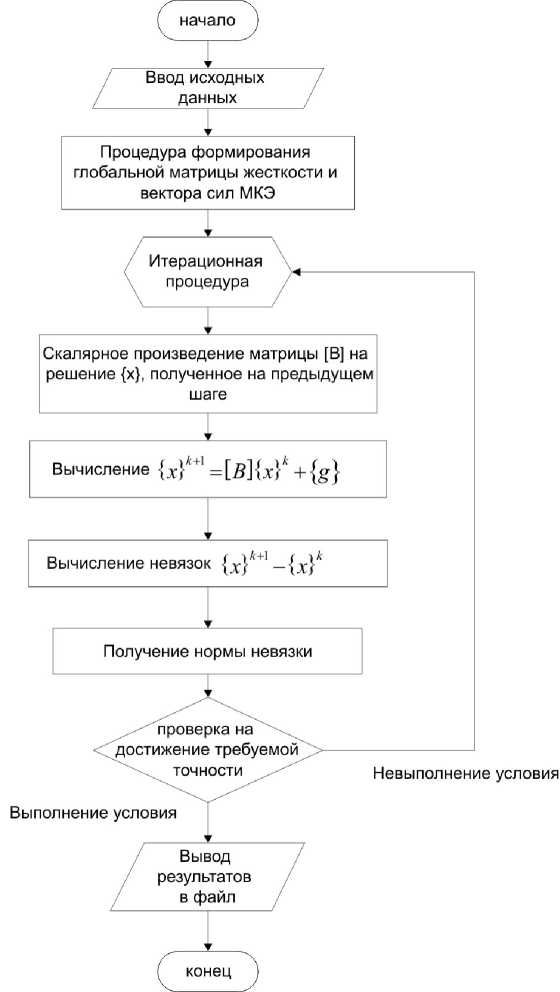
Рис. 7. Схема метода Якоби

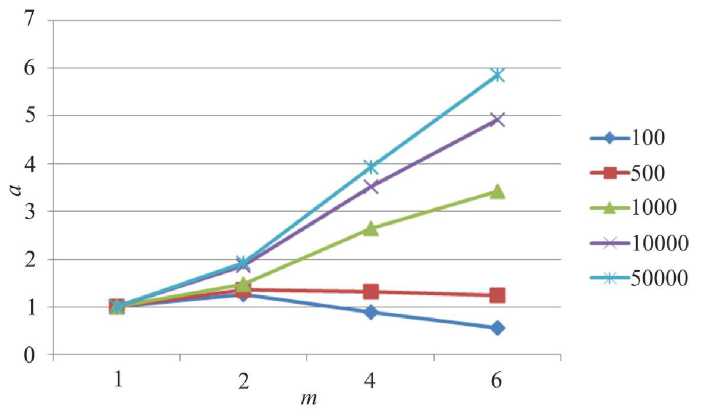
Рис. 8. Зависимость ускорения а параллельного алгоритма от числа процессоров m для сеток разной размерности в параллельной модели без мастер-процесса

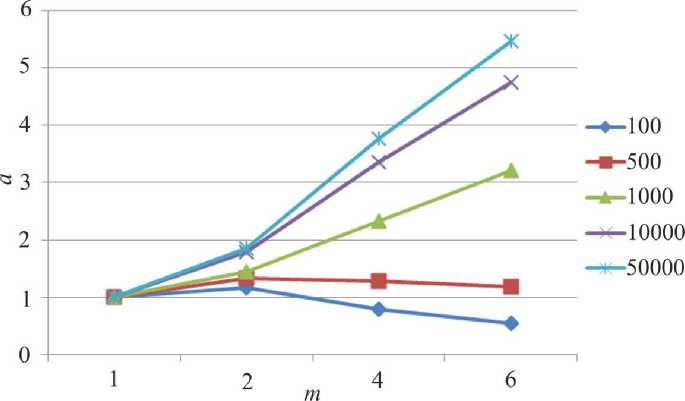
Рис. 9. Зависимость ускорения а параллельного алгоритма от числа процессоров m для сеток разной размерности в параллельной модели, содержащей мастер-процесс

На рис. 8 и 9 представлены зависимости ускорения от числа параллельных процессов для систем различной размерности с использованием и без использования мастер-процесса. Аналогично методу сопряженных градиентов наблюдается снижение коэффициента ускорения для задач малой размерности. Близкие результаты обеих схем распараллеливания объясняются малым числом векторных операций в методе Якоби.

Заключение

Полученные данные позволяют сделать вывод, что использование мастер-процесса при параллельной реализации метода сопряженных градиентов приводит к незначительному, от 10 до 15 процентов, снижению величины коэффициента ускорения по отношению к варианту реализации, не использующему мастер-процесс. В случае использования метода Якоби эффект выражен намного слабее. Принимая во внимание структурное удобство использования идеологии мастер-процесса, применение данного архитектурного решения при реализации рассмотренных методов предпочтительнее.