Эффективность подпространственных сетевых кодов

Прежде всего введём обозначения и определения. Пусть W = GF ( q ) ⁿ — основное п-мерное пространство над конечным полем GF ( q). W(n,m) — множество всех m-мерных подпространств основного пространства W, называемое грассманианом.

|W (n, m)| = [”]

(qⁿ - 1)(qⁿ - q) ... (qⁿ - q^m-1)

(qm

- i)(q^m - q)... (q^m -q^m-1)^.

Грассманово расстояние между двумя подпространствами U,V Е W(n,m) определено следующим образом:

d_S ub (U, V ) = dim(U W V) - dim(U nV) =

= dim(u) + dim(V) - 2 dim(U nV) = = 2m - 2 dim(U nV) = 25.

Обозначим [n, M, d_su b = 25, m] некоторый код в грассмаіювой метрике, у которого п — длина кодовых слов, M — число кодовых слов, d_su b — минимальное кодовое расстояние, m — размерность.

Верхняя граница, мощности грассмановых кодов получена, в 2003 году [1]:

^{5 + 1)1} = [m-5+1]

| W(n, m -

Mmax 6

|W(m,m - 5 + 1)|    [m-m+i] .

Асимптотическая форма, этой границы имеет вид

M_max 6 q^^{N -m})(^m-^⁺¹) + q^(N-m)(m-+1W(1 + 0(1)).

На рис. 1 показана зависимость мощности кода от его длины для размерностей m = 3 л m = 4.

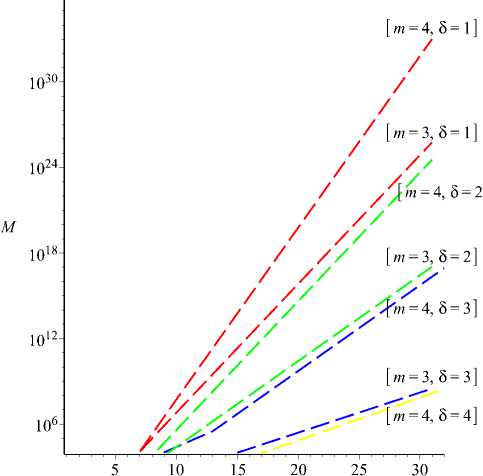
Рис. 1. Зависимость мощности кода, от длины

Приведём расчёты верхней границы при заданных параметрах п, 6, т, где п >  2т.

Таблица!

Верхняя граница мощности кода, т = 3

п	7	9	15	30
Mmax, 6 = 1	11811	788035	2 . 09 • 1011	7 . 4 • 1024
Mmax, 6 = 2	381	6205	2 . 60 • 10 7	2 . 7 • 1016
Mmax, 6 = 3	18	73	4681	1 . 5 • 10 8

Т а б л и ц а 2

Верхняя граница мощности кода, т = 4

п	7	8	9	15	16	30
Mmax, 6 = 1	11811	200787	3 . 3 • 10 7	5 . 7 • 1013	9 · 1014	6 . 6 • 1031
Mmax, 6 = 2	787	6477	52535	1 . 3 • 1010	1 . 1 • 1011	4 . 9 • 1023
Mmax, 6 = 3	76	308	1241	5 . 1 • 10 6	2 . 0 • 10 7	5 . 5 • 1015
Mmax, 6 = 4	---	17	34	2184	4369	7 . 2 • 10 7

Как видно из рисунка и расчётов, Mmax растёт с ростом длин п. Кроме того, чем больше размерность т, тем больше мощность Mmax при том же кодовом расстоянии 6. Чем больше 6, тем меньше Mmax при том же т и фиксированном п.

В настоящее время известны подпространственные коды большой мощности. К ним относится случайный сетевой код (SKK-код), разработанный тремя авторами - Силвой, Кёттером, Кшишангом [2-3], многокомпонентный код с нулевым префиксом (МНП-код), предложенный Габидулиным и Боссертом 2008 году [4-5] и дополненный оптимизацией параметров в 2012 году [6]. Кроме того, разработан Шишкиным многокомпонентный код [7], основанный на лексикографическом принципе и оптимизации с отбраковкой. Имеются также отдельные примеры подпространственных сетевых кодов, использующих в качестве основы ранговый код Габидулина [8] и так называемые диаграммы Феррера [9-10]. Однако отдельные примеры не дают возможности определить мощность кодов при всех возможных значениях параметров, поэтому здесь ограничимся анализом характеристик SKK- и МНП-кодов.

2.    Случайный сетевой код SKK

Кодовая матрица SKK-кода имеет вид

С = {[Im M]} , где Im - единична я матрица, М - матрица рангового кода над базовым полем GF (q) Мощность этого кода такова:

M_skk = q^^, _{гдек = m} — 5 _{+ 1}.

Зависимость от длины кода показана на рис. 2.

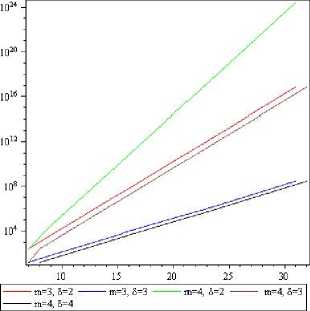
Рис. 2. Мощность кодов SKK в зависимости от длины кода

3.    Многокомпонентный сетевой код МНП3.1.    Структура кода

В 2008 году Габидулиным и Боссертом предложен многокомпонентный сетевой код: это код с нулевым префиксом ^МНП-код^ [4-5].

Пусть Mi, г = 1,... ,т - кодовая матрица г-й компоненты. Компоненты имеют следующую структуру:

Mi =ImMi,

М2 = O⁵m ImM₂, . . .

м = о5 о5   о5

iviт — ^m^m . . . v/m1mlvlr, где первая компонента Mi - это SKK-код. Как видно из этой структуры, перед каждой следующей компонентой появляется матрица из m-строк и 5-столбцов, состоящая из одних нулевых элементов. В результате число столбцов матрицы рангового кода уменьшается на. 5.

3.2.    Мощность кода

Благодаря тому, что все эти компоненты в подпространственном смысле ортогональны, общая мощность многокомпонентного кода равна сумме мощностей всех г кодовых компонент Mi, г = 1,г.

Зафиксируем параметры п, т, 6 и подсчитаем мощность.

Мощность МНП-кода состоит из трёх частей:

МмнП = Mskk + Si + S2 + 1, где

«1

=    ^ к ^ п - т -Й)

i =i

S2 = ^2кіт.

i =i

Здесь М₈ кк ~ мощность нерв ой компоненты, Si - суммарная мощность компонент, начиная со второй до si-й, S2 - суммарная мощность компонент, начиная с ((si) + 1)-й до последней компоненты. Параметры si, S2, к г выбираем в соответствии с алгоритмом построения кода: si-й сдвиг длин кодовых слов происходит при выполнении условия п—т—si6 = т+у, где 0 < у < 6 — 1. Так что si = ^п -2 т - ^ . Далее происходит уменьшение длины на 6 (т + у — 6 < т) и транспонирование кодовой матрицы.

Теперь сторона длины т + у — 6 - размерность, которая уменьшается на 6 на каждом шаге. Множитель в показатели степени к г = (т + у — г6) — 6 + 1.

Параметр S2 определим из условий

6 < т + у — s₂6 и т + у — (s₂ + 1)6 <  6 :

т + у — 26       т + у — 6

6      < S2 <     6.

Пример 1. Пусть п = 70, т = 15, 6 = 3. Здесь у = 1. s1 = ^{п -}2 т - ^ = Z⁰-!⁰-! = 13

15+1-6         15+1-3

3   < s2 <3

С учётом целочисленности получаем S2 = 4. Мощность этого МНП-кода равна

МЛпга = 2 3  + £ 2i3(55-3i) + £ 2i5(i4-3i) + 1.

i=ii=i

Функция разности мощностей АМ = Ммнп — М₈ кк в зависимости от п при фиксированных параметрах т и 6 представлена на рис. 3. Из рисунка видно, что функция АМ растет при увеличении п и зависит от т и 6.

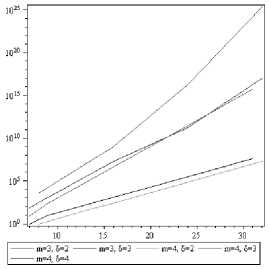
Рис. 3. Функция АМ в зависимости от длины кода

3.3.    Оптимальность кода МНП

Доказано [6], что МНП -код имеет максимальную мощность при следующих параметрах: 6 = тип = 1т.

qⁿ — 1   9^/m — 1

^Mnax =    - 1 =     - 1 ,                            11)

где I - целое число. Если п = 1т + s, 1 6 s < т, то мощность этого кода выражается формулой

M = g(/-1)m+a + 9(/-2)m+s +_____+ ^m+s + 1.

Пример 2. Рассмотрим два случая. Пусть 6 = т = 4 и п = 15, s = 3. Используем формулу (2) и получаем

M = 2^(3-1)4+3 + 2^(3-2)4+3 + 1 = 2177.

Верхняя граница в этом случае даёт значение Mmax=2184, то есть относительная разность равна ^max-^=0.0032. Пусть 6 = т = 4 и п = 17, s = 1. Используем формулу (2) и получаем

M = 2^(4-1)4+1 + 2^(4-2)4+1 + 2^(4-3)4+1 + 1 = 8737.

Верхняя граница в этом случае даёт значение M_max=8738, то есть Мд ^М =0.0000114. В обоих случаях оценка по формуле (2) близка к верхней границе (1).

4.    Эффективность SKK- и МНП-кодов

Определим эффективность кодов в виде отношения мощности данного кода, к максимальной мощности, определяемой верхней границей, при фиксированных параметрах п, т, 6;

Л_акк = ^ ^кк ~ эффективность SKK-кода;

Ло = Мм™ ~ эффективность МНП-кода.

Приведём расчёт эффективности этих кодов при фиксированном п = 16 и различных значениях параметров т, 6.

Т а б л и ц а 3

Длина кода п = 16, расстояние 6 = 2

т	2	3	4	5	6	7	8
Л акк	0.750	0.656	0.615	0.596	0.587	0.583	0.581
Ло	1.000	0.700	0.625	0.598	0.587	0.583	0.581

Т а б л и ц а 4

Длина кода п = 16, расстояние 6 = 3

т	2	3	4	5	6	7	8
Л акк	_	0.875	0.820	0.794	0.782	0.777	0.774
Ло	-	1.000	0.823	0.796	0.782	0.777	0.774

Т а б л и ц а 5

Длина кода п = 16, расстояние 6 = 4

т	2	3	4	5	6	7	8
Л акк	-	-	0.938	0.908	0.894	0.887	0.887
Ло	—	—	1.000	0.912	0.908	0.887	0.887

Длина кода п = 16, расстояние 6 = 8

т	2	3	4	5	6	7	8
Л зкк	—	—	—	—	—	—	0.996
Ло	-	-	-	-	-	-	1.000

Длина кода п = 16, расстояние 6 = 5

т	2	3	4	5	6	7	8
Л зкк	-	-	-	0.969	0.954	0.946	0.942
Ло	-	-	-	0.999	0.954	0.946	0.942

Длина кода п = 16, расстояние 6 = 6

т	2	3	4	5	6	7	8
Л зкк	—	—	—	—	0.984	0.977	0.973
Ло	—	—	—	—	0.985	0.977	0.973

Длина кода п = 16, расстояние 6 = 7

т	2	3	4	5	6	7	8
Л зкк	—	—	—	—	—	0.992	0.988
Ло	—	—	—	—	—	0.994	0.988

Т	а.	б	л	и	ц	а.	6
Т	а.	б	л	и	ц	а.	7
Т	а.	б	л	и	ц	а.	8
т	а.	б	л	и	ц	а.	9

Приведённые расчёты показали,что эффективность МНП-кода всегда больше или в некоторых случаях (при заданной точности 3 знака после запятой) равна эффективности SKK-кода. При условии т = 6 1і ^ ~ целом эффективность МНП-кода равна. 1. то есть совпадает с верхней границей.

5.    Заключение

• •    Проанализирована, верхняя граница, мощности подпространственных кодов в зависимости от основных параметров. Показано, что мощность увеличивается при увеличении длины, а. также размерности кода, и уменьшается при увеличении кодовых расстояний.

• •    В качестве нижней границы предложено использовать мощность многокомпонентного кода, с нулевым префиксом (МНП-кода?) Габидулина - Боссерта. Мощность МНП-кода больше мощности случайного сетевого кода Силвы-Кёттера-Кшишанга ( SKK- кода)при всех значениях основных параметров. В случаях равенства, кодовых расстояний и размерностей мощность МНП-кода практически (в некоторых случаях точно) совпадает с верхней границей мощности.

• •    Оценена эффективность кодов SKK и МНП и приведены расчёты эффективности (с точностью до третьего знака после запятой) для следующих параметров: п = 16, т = 2, 3,4, 5, 6, 7, 8, 6 = 2, 3,4, 5, 6, 7, 8, где п > 2т. Показано, что при такой точности и больших размерностях эффективность SKK-кода и МНП-кода практически одинакова. Так что в этих случаях можно использовать мощность любого из рассматриваемых кодов в качестве нижней границы мощности подпространственных сетевых кодов.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 15-07-08480 А.