Эффективность преобразования поточных процессов в тепловых расходных машинах

Самарский научный центр РАН

Проведен анализ эффективности широкого класса газовых машин, в котором в явном виде технической работы не совершается - это вихревые устройства различного предназначения, химические газовые реакторы, эжекторы, плазматроны, смесители, акустические газовые устройства и т.д. На основе ранее доказанной автором теоремы построен предельный цикл указанного класса машин. Представлено графическое обобщение всего пространства тепловых машин.

В работе [1] доказана предельная энергетическая теорема для широкого класса теплоэнергетических устройств, в которых техническая работа не реализуется в явном виде "  .. ⁰>.

В данной работе под термином "расходная тепловая машина" подразумевается система или устройство, в котором специально организованный газовый поток осуществляет полезную внутреннюю работу1 над самим рабочим телом.

Например, в сверхзвуковом закрученном потоке газа в вихревых трубах происходит сепарация энергии на холодную (на оси трубы) и горячую (на периферии) составляющую потока газа [2]. В данном случае полезной внутренней работой является работа сепарации газового потока за счет сил турбулентного трения.

Другим примером полезной внутренней работы в расходных тепловых машинах могут служить газовые акустические устройства, в которых происходит преобразование части энергии газового потока в энергию акустических колебаний среды.

К данному классу расходных тепловых машин могут быть отнесены следующие устройства:

• 1.    Химические газовые реакторы различных типов.

• 2.    Тепломассообменные газовые устройства (вихревые трубы различных типов, эжекторы, смесители, газовые акустические устройства и т.д.).

• 3.    Энергетические устройства, имеющие в качестве рабочего тела до- и сверхзвуковой

4. Химические сепараторы и др.

потоки газа (лазеры и плазматроны различных типов и т.д.).

Общим свойством указанного класса тепловых машин является тот факт, что их эффективность тем выше, чем выше степень преобразования энергии газового потока в потенциальную энергию давления (в ракетных двигателях, например, полная энергия преобразуется в кинетическую). На рис.1 представлена принципиальная схема тепловых машин указанного типа.

В адаптированном варианте для случая одного входа и выхода (рис.1) доказанная предельная энергетическая теорема может быть сформулирована следующим образом: к.п.д. расходной тепловой машины не может превысить величины Д Н_тах ,

где

Ж max

Q =

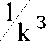
Карно

+

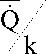
1 + Q

Q

__ ___* • •

CpT G;

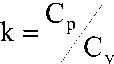
^з Карно

= 1 —

Т 1

Т к .

К.п.д. расходной тепловой машины - это отношение полезной внутренней работы, совершаемой газовым потоком, к полной энергии, подведенной к машине.

Доказат ельст во:

Введем следующие обозначения:

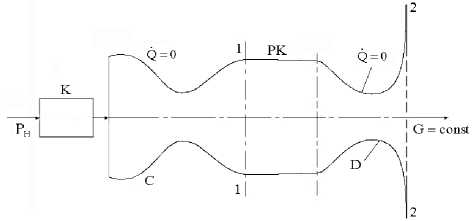
Рис. 1. Принципиальная схема расходной тепловой машины (L =0).

К - компрессор; РК - рабочая камера;

D - диффузор; Рн, РК - давление на входе и на выходе из компрессора соответственно; С - сопло

ности на входе и определим предел этого выражения при стремлении к нулю выходной скорости v₂ ^ 0 .

Получим следующее выражение:

г<

д ы .

= lim kk - 2 ^ 0

Pi   v 2 V •

¹ + -1- G + Q c,    2

<

^^^^^^^.

P 2 + ^-' Ь

C p T , G + Q

с2    2

и .(4)

В результате обезразмеривания, учета уравнения энергии и элементарных преобразований окончательно получаем:

Р 1 , с 1 , - 1 , Р₂, с₂, -₂ - давление, плотность и скорость на входе в рабочую камеру и выходе из диффузора соответственно;

C v , С_р, T 1 , G , Q - теплоемкости при постоянном объеме и давлении, температура торможения на входе в рабочую камеру, расход и подведенная в рабочую камеру тепловая мощность соответственно;

Т_к, Т 1 - статическая температура на входе и выходе из сопла (С) соответственно.

В случае отсутствия технической работы ( Ь_тех = 0 ) и разности геометрических

A N

max

^{1 +}

_

1 k — 1 k ‘ k + 1

7 k — ¹

k + 1 k

e

+ Q

k — 1

1 + Q ^k

^X 2 + ^ k

■

1 + Q

Газодинамический к.п.д. цикла Карно для теплоизолированного сопла определяется по формуле:

высот входа и выхода g ( z 2 — z 1 ) = 0 нение теплового баланса имеет вид

урав-

^з Карно

= 1 —

Т

т

К

C T.G + 1G + -Gg + Q =

v1          2

Т

*

(

1—

= 1 —

k — 1

k + 1

Л 2

c 1

T 1^*

]

k — 1

k + 1

^ё 1 ,

= C vT2G + 2G + —2G

^{v 2} c ₂        2

^2k *

где Л1 =       RT1 - коэффициент скорос- k +1

Отсюда ДО = ДЫ, где ДО = C-(T2 - T1 )G - изменение внут-

ренней энергии потока в единицу времени.

Изменение мощности газового потока и подведенной извне тепловой мощности на входе и выходе равно:

ти потока на входе в рабочую камеру;

статическая температура после компрессора Т_к равна полной температуре на входе в сопло Т = Т * .

К 1

Следовательно формулу (5) можно переписать в следующем виде:

Д N =

f Pl+

I ^с 1

^- 1

G + Q

^^^^м

—■

( ^с 2

^- 2

■

G .(3)

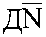
max

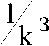
Карно

+

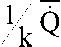
I

1 + Q

Отнесем изменение ДОв расходной тепловой машине к полной тепловой мощ-

Максимальный к.п.д. расходной тепловой машины:

з т > 0 = Д Н_тах - (8)

В формуле (8) индекс (G > 0) означает, что расход через тепловую машину не равен нулю.

Выражение (7) представляет собой максимально возможное значение относительной доли мощности потока и подведенной тепловой мощности, потерянной и (или) утилизированной в расходной тепловой машине.

Вследствие того, что скорость отводящих газов отлична от нуля и всегда имеются потери, к.п.д. расходной тепловой машины будет меньше предельного значения (7):

A N <  A N max .

Что и требовалось доказать. Таким образом, получена мажорантная оценка к.п.д. расходной тепловой машины при Етех = 0.

Следствие. Глобальный максимум утилизированной и (или) потерянной мощности в тепловой расходной машине при Етех = 0 равен:

^lmU^N = ^limД^N max = lim^ max a^n max       q _у^       Л^Л тах

Q ^                  Q ^1

£ k.

ловых машин включает сопло, рабочую камеру и диффузор с бесконечно большим расширением. Как отмечено выше рассматриваемый класс машин имеет тем большую эффективность, чем выше степень утилизации кинетической энергии Екин в энергию давления Едавл. Для идеальной тепловой машины указанного класса максимальная степень утилизации кинетической энергии достигается при бесконечном уширении диффузора

8диф ^ ^, а значит скорость на выходе из диффузора стремиться к нулю ( v2 ^ 0 ) при постоянном расходе (G = const).

На рис. 2 представлен условный холостой цикл для указанного класса машин при

Q i ^ 0 .

Следует отметить, что тепловые маши ны указанного класса являются принципиально открытыми. Однако, использование графического изображения рабочего цикла, также как для ВРД, РД (цикл Брайтона) допу- стимо.

Идеальный цикл, представленный на рис. 2, состоит из одной изотермы (Н-К), двух идеальных адиабат (К-3, 4-Н) и одной ударной адиабаты Гюгонио (4-3). Следует отме тить, что при сверхзвуковом режиме течения

Из рис.1 видно, что указанный тип теп

1 ) всегда имеет место скачок уплотне-

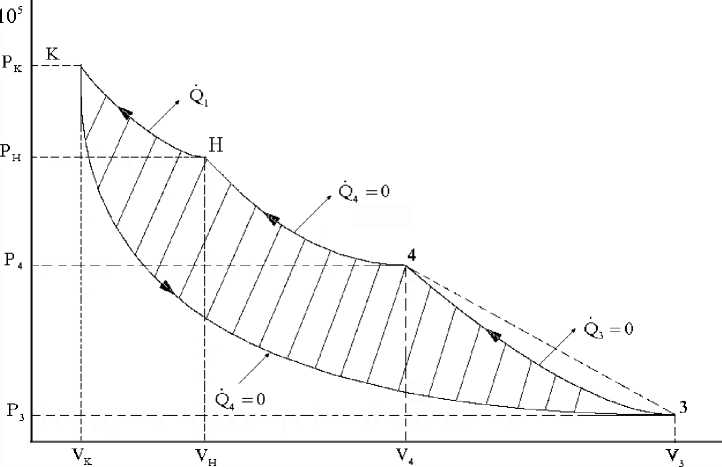
Рис. 2. Условный предельный цикл холостого хода тепловой расходной машины

⁽ ^ тех

- отведение, подведение теплоты к машине

= 0 ) Q i

ния, так как режим течения в сопле является нерасчетным [3].

Потерянная ( дЫ ) или утилизированная мощность ( з _G > 0 ) в тепловой машине указанного класса не может превысить максимальную возможную величину ( ДЫ_тах или з ^т>о )» определяемую теоремой [1].

Заштрихованная площадь Н-К-3-4-Н, отнесенная к общей площади по кривой КН-4-3, и представляет собой относительную долю потерянной ДЫ_тах или утилизированной з о > 0 мощности.

J Pdv з G>0 = ДЫ = 1 - к------K------н    -(10)

J Pdv + j Pdv + J Pdv

H        3        4

Как утверждает теорема, данная величина не может превысить соответствующее максимальное значение, определяемое [1] по формуле (1)

з о>0 <  з т> ^х 0 = ДОтах ’   (1¹)

Следует отметить, что в координатах Р-V в общем случае траектория ударной адиабаты Гюгонио не определена, а имеются только начальные (P3, V3) и конечные (P4, V4) значения траектории. Для случая слабых ударных волн в работе [4] получено решение задачи о кривизне траектории адиабаты Гюго нио

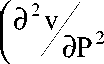
> 0 . Однако экстраполяция данного результата в области сильных удар ных волн не аргументирована.

Второе начало термодинамики и теорема о минимуме производства энтропии И. Пригожина [5] не позволяет определить форму кривой 4-3 без допущения о локальном равновесии в зоне скачка уплотнения. Производная по времени от производства энтропии будет отрицательной:

dP          dS

— < ⁰ , где ^P = — > ⁰ , т.е. dS >  0 . (12)

Таким образом, устойчивость термодинамического процесса выполняется при варьировании формы кривой в широком диапазоне.

Для выяснения формы кривой на участ ке (4-3) используется значение з т>о д™ сду- чая Q = 0 :

max з О >0 = Д^тах

1         1k - 1 ₂

= ^з Карно =         ^ё 1 .⁽¹³⁾

k        k k + 1

Площадь цикла по формуле (10) числен но определялась для з = ДЫ при варьировании давления на выходе из машины (Рн) и фиксированном значении PK = PK .

В первом приближении на участке 3-4 использовалась линейная зависимость между Р и V.

В этом случае площадь под кривой 3-4 определяется как площадь трапеции:

j PdV = ^(Р 3 + ^Р 4 ) ( V₃ - V₄ ) . (14) 4 ²

На рис.3 показано, что утверждение теоремы удовлетворяется в диапазоне до PH = 0,05 -105Па, т.е. до скоростей на вхо де в камеру Л1 = 2,307 .

При дальнейшем понижении давления на выходе из диффузора Р_н< 0,05 з = ДЫ становится больше, чем з ^тах , что запрещается теоремой.

Теорема будет удовлетворена при вы-

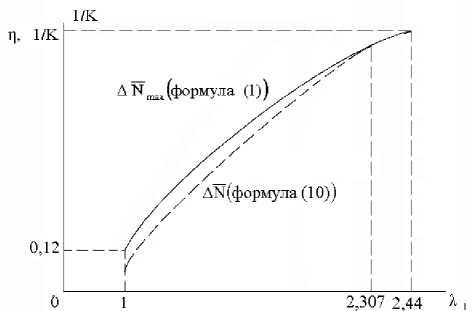
Рис. 3. Зависимость П от % полнении условия jpdv <(Ъ±^-'(V3 - V), (15) 3             2

т.е. траектория 3-4 должна быть вогнута (рис. 2).

Таким образом, теорема [1] позволяет определить форму траектории условного процесса на участке ударной адиабаты в P-V координатах.

Теорема И. Пригожина [5] (формула (4)) в данном случае выполняется автоматически:

циклу двигателя, а обратный - холодильной машине, может работать в одном и том же направлении, как холодильная машина (например, вихревые трубы) и в ином качестве (например, газовые эжекторы).

Эффективность энергетических установок рассматриваемого класса тепловых машин может быть определена индикатором качества поточного процесса I, равного отношению полезной внутренней работы к максимально возможной доле энергии, которая может быть утилизирована в данный момент:

dS2 dt2

< 0,

где S = C_Vln

PVк р vK P3V3

+ S 3 , (16)

I =

А пол

AN_m ax

где S - термодинамическая энтропия; Cv -удельная теплоемкость газа при постоянном объеме; Р3, V3, Р, V - давление и удельный объем перед скачком и после него на участке 3-4; S3 - значение энтропии потока перед скачком при V = V3 и Р = Р3.

На рис. 4 холостой цикл тепловой машины представлен в Т-S координатах. Так как цикл замкнут, то согласно определению энтропии (16), несмотря на участок с необратимыми потерями (скачок уплотнения 3-4), суммарное изменение энтропии равно нулю. Следовательно, учитывая, что на участках адиабатического расширения (2-3) и сжатия (4-1) по определению изменение энтропии равно нулю, повышение энтропии на участке скачка уплотнения (3-4) в точности равно понижению энтропии на участке изотермического сжатия в компрессоре (1-2)

AS 34

**

= AS^ = Rln- 2 = Rln 3г;

12              **

Р1

да1 = AS,, + Д823 + Д334 + да41 = одт)

В отличие от цикла Карно, где движение возможно в прямом и обратном направлении, в данном цикле движение возможно только в одном направлении, т.е. цикл является необратимым при суммарном изменении энтропии равном нулю.

При этом указанный цикл, в отличие от цикла Карно, где прямой цикл соответствует где Апол - полезная внутренняя работа рабочего тела.

Полная эффективность указанного класса машин определяется следующим образом:

N з^ = П зi, где i =1, 2, n. (19) i=1

Например, для проточного газового лазера с электрической накачкой полная эффективность (или к.п.д.) запишется так:

з ?   = з ■ з к • з ■ з ,   (20)

laser г.т обсл. эо кв

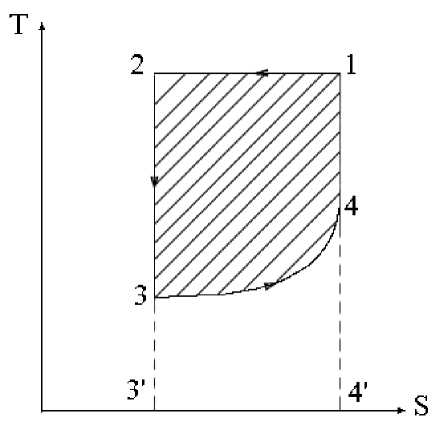
Рис. 4. Предельный цикл тепловой машины в T-S координатах

1-2 - изотермическое сжатие в компрессоре;

2-3 - адиабатическое расширение в сопле;

3-4 - скачок уплотнения; 4-1 - адиабатическое сжатие в диффузоре

Таблица. Классификация тепловых машин по способу преобразования полной энергии рабочего тела

Класс тепловых машин	I	II	III
Расход газообразного рабочего тела	G = 0	G > 0 G — G max	G > 0 (G — G max )
Скорость газа на выходе из тепловой машины	VBbI х = о вых	V„ > 0 (V ^ V ) \ вых      max /	V вых — 0 ( SBy х —— ^ ) вых
Направление преобразования полной энергии газового потока	Полная (внутренняя) энергия преобразуется в механическую работу Е = Е      А пол     внутр    ^мех	Полная энергия преобразуется в кинетическую энергию Е    Е пол      кин	Полная энергия преобразуется в потенциальную энергию давления Е    Е пол       пот
Коэффициент полезного действия	ideal _ Л    Т 2 з Карно 1   гр 1 1 • ; з Стирлинга и т.д.	n—1 з = 1 -(1" 1 n V r 1 J г.ideal шпз — з Карно P1 ——^	а)    ^ тех 0 ideal    1 ideal з G>0    k з Карно б)    Q внеш    0 ; L тех ^ 0 ideal      ideal з    = з       е з       з Карно е
Цикл тепловой машины	Цикл Карно Цикл Стирлинга	Цикл Брайтона	Цикл расходной тепловой машины (рис.2)

где з_г . _т . = I • з ¹^ ; 3_0бсл . - это эффективность газового тракта, эффективность обслуживающего лазера; з _эо , 3 _кв - это электрооптическое и квантовое к.п.д. газового лазера.

Так для СО,-лазера з „„ ~ 0,4 , а для СО-2 ^А кв ^{7 7}

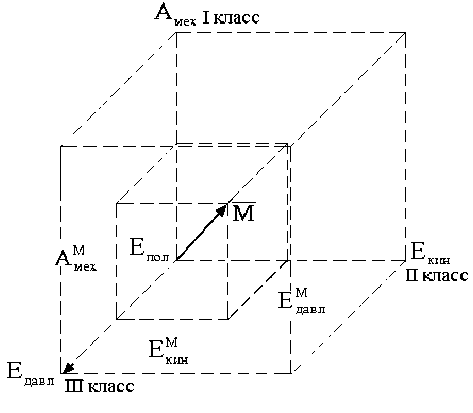
Рис. 5. Принципиальная схема пространства тепловых машин лазера з кв ~ 0,8 соответственно, т.е. полное к.п.д. лазерной установки даже в идеальном случае ( з эо = з обсл = 1) не может превысить для СО2 и СО-лазеров соответственно величин:

з ^ = —чСО2    25

^з ideal = ^з кв ~ ⁰,²⁵ CO ₂   K

и з ^ з СО ~ 0 5

^з ideal = ^з кв ~ ⁰,⁵ • CO K

В таблице представлена классификация тепловых машин, характеризующаяся направлением преобразования полной энергии, подведенной к тепловой машине.

На рис.5 представлена графическая иллюстрация таблицы. Видно, что классы тепловых машин (I, II, III) можно изобразить в виде куба со сторонами Епол - Амех - Епол - Екин,

Весь объем пространства куба представляет собой всё многообразие комбинирован- ных схем указанных классов тепловых машин. Вектор M определяет энергетические характеристики некоторой тепловой машины М.

1 Под внешней полезной работой подразумевается техническая работа, которая для данного класса машин равна нулю (Ьтех = 0).