Эффективные диффузионные уравнения дробного порядка: обобщенный закон Фика и асимптотические решения

Как известно стохастический транспорт в неупорядоченных системах интенсивно изучается в последнее время. Это связано как с аномальным характером транспорта в этих системах, так и с возможными многочисленными приложениями [1-3]. Один из наиболее известных примеров аномального транспорта является случайные блуждания на перколяционных кластерах, которые носят субдиффузионный характер:

< x 2 ( t ) >« t^d w

Здесь d w - критический индекс аномальной диффузии (d w >  2). В целом к настоящему моменту сложилось общее представление о необходимости как использования устойчивых распределений негаус-сового вида, так и математического аппарата дробных производных и интегралов для описания аномального стохастического транспорта [4-6]. В частности, было показано, что при описании субдиффузионных стохастических процессов возникают эффективные диффузионные уравнения дробного порядка по времени [7, 8]. В работе [9] было выведено уравнение диффузии с дробной производной по времени порядка ½, описывающее диффузию вдоль оси гребешковой структуры:

5 ¹/² N ( x , t ) _ D а ² N ( x , t ) a t^1/2    "      ax¹

Следует отметить, что гребешковая модель является одной из немногих точно решаемых моделей с субдиффузионным характером, поэтому она использовалась многими исследователями [10-14]. Например, гребешковая модель была использована и при исследованиях массо-переноса в живых организмах и роста раковых клеток в работах [15-17]. Аналогичные эффективные уравнения дробного порядка возникают также при опиcании транспорта пассивного скаляра в задачах переноса [18-20]. В работе [21] было показано, что решения эффективных уравнений дробного порядка существенно за- висят от начальных условий.

В настоящей работе выполнено исследование анизотропных случайных блужданий на многомерной гребешковой структуре. Проблема заключается в том, что в отличие от анизотропных случайных блужданий при обычной диффузии анизотропные случайные блуждания на многомерной гребешковой структуре имеют различные степенные зависимости [22, 23]. В двумерном случае кри- тические индексы равны:

d wx = 4, d wy = 2                                                  (3)

В трехмерном случае гребешковой структуры эти индексы принимают иные значения:

d wx = 8, d wy = 4, d wz = 2                                           (4)

Различные степенные зависимости среднеквадратичного диффузионного смещения вдоль разных координат означают также и различные автомодельные поведения вдоль этих координат, которые при раздельном рассмотрении вдоль каждого направления описываются соответствующими уравнениями дробного порядка типа (2). Возникает вопрос – возможно ли унифицированное описание анизотропных субдиффузионных случайных блужданий на гребешковой структуре? И если да, то каким должно быть искомое обобщенное диффузионное уравнение, описывающее унифицированным образом анизотропную аномальную диффузию на многомерной гребешковой структуре?

Целью работы является развитие подхода для описания анизотропных субдиффузионных случайных блужданий и вывод обобщенного диффузионного уравнения для исследуемого случая. Получено обобщение известного закона Фика для обычной диффузии [24]:

^-            ^

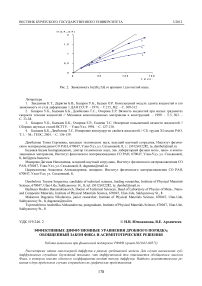
• jd =— D V n

на случай для задач анизотропного многомерного массопереноса в рамках гребешковой модели. Показано, что в этом случае возникает эффективный тензор диффузии, компоненты которого имеют операторный вид и содержат производные по времени дробного вида. Получены асимптотические уравнения диффузии для анизотропного многомерного случая. Установлено, что в анизотропном случае возникают многомерные распределения Коши, описывающие аномальную диффузию в обратном ( s , k ) - пространстве.

Диффузия в модели гребешковой структуры

Гребешковую модель впервые введена для описания субдиффузии на перколяционных кластерах [23, 24]. Она состоит из хорошо проводящей оси (аналог скелета перколяционного кластера) и ребер, прикрепленных к оси – рис. 1.

Рис. 1. Гребешковая модель: ось и ребра, прикрепленные к оси структуры

Особенность диффузии в гребешковой структуре состоит в возможности смещения по Х -направлению только вдоль оси структуры (при y = 0). Это означает, что коэффициент диффузии D xx отличен от нуля только при y = 0:

D xx = D i 5 (y),

X – компонента диффузионного тока равна : J x

- D

xx

5 N

8 x

Диффузия вдоль осей структуры носит обычный характер: D xx = D 2 . Следовательно, случайные блуж-

дания на гребешковой структуре описываются тензором диффузии:

_ ( D 1 5 ( y )    0 )

j I 0 D 2 J

Используя закон Фика с тензором диффузии (7): ^{J d}

( -— D 1 5 ( y ) — - D 2 — ^d t             d x ² d ² y

^-

= -D VN получим диффузионное уравнение:

) G ( x , y , t ) = 5 ( x ) 5 ( y ) 5 ( t )

Здесь G ( x, y, t ) – функция Грина уравнения диффузии. Для дальнейшего удобства сделаем преобразование Лапласа по времени и преобразование Фурье по x – координате:

[ 5 + D 1 k² 5 ( y ) - D ₂ d— ] G ( 5 , k , y ) = 5 ( y ) a y

В качестве начальных данных используется точечный источник (8) будем искать в виде:

G ( 5 , k , y ) = g ( 5 , k ) exp( - 2 | y |)

(9) δ ( x ) δ ( y ) δ ( t ) . Решение уравнения

Подставляя решение (10) в уравнение получим две части: регулярное выражение и выражение с сингулярным коэффициентом δ ( y ) :

[ 5 - D 2 A²]G ( 5 , k , y ) = 0

[ D i k ² + 2XD ₂ ] 5 ( y ) g ( 5 , k , y ) = 5 ( y )

Из первого уравнения (11) мы определим значение параметра λ ражение для функции g( s, k ):

^X DZ^ ^{g ( 5} ’ k ) = 2 D 2 Л + D ₁ k²

,

а из второго уравнения (12) вы-

Рассмотрим диффузию вдоль оси гребешковой структуры при ^y 0 . Для этого сделаем обратное преобразование функции g( s, k ):

exp( ikx + st ) dkds G ( x ,0, t ) = JJ —

2 D ₂ X + D 1 k ²

Используя тождество:

j exp(

— ат ) d т = — α

получим выражение для функции Грина, описывающее диффузию вдоль оси структуры:

^J          I

G ( x ,0, t ) = J т exp I —

0         (

x ² D 2 ( τ ) ²

—

4 D ₁ τ       4 t

D 2³

₁ t 3 τ

Отметим, что число частиц на оси структуры убывает, т.е диффузионная задача для диффузии вдоль оси оказывается задачей с несохраняющимся числом частиц

< G ( t ) >= J G ( x ,0, t ) dx = , 1 ₀                  2 D ₂ t

Исходя из этого, вычислим среднеквадратичное смещение вдоль оси гребешковой структуры:

< ^{x 2 ( t} ) >= Dj^i D;

Таким образом, случайные блуждания вдоль оси оказываются субдиффузионными с критическим индексом d wx = 4. Диффузия вдоль ребер гребешковой структуры носит обычный характер:

< y ²( t ) >= 2 D 2 t

Таким образом, анизотропные случайные блуждания описываются различными степенными зависимостями (18) и (19) [24].

Обобщение закона Фика в двумерном и трехмерном случаях

Чтобы получить обобщенное уравнение диффузии в двухмерном случае рассмотрим подробнее решение (10). Для этого сделаем Фурье преобразование этого решения по координате y:

G ( s , k x , k y ) =

2 λ

(2 D ₂ X + D 1 k ²)( X ² + k y )

Соответственно, получим следующее уравнение диффузии для анизотропных случайных блужданий на гребешковой структуре:

k ²

(2 D 2 X + D i k ²)( - + - y ) p ( s , k x , k y ) = 0

2  2 λ

Пренебрегая в полученном уравнении произведением k X х k y ² (это возможно на больших масштабах), получим следующее эффективное уравнение в (s, k x k y ) – представлении:

D 1   2

s +---- k _r 2 ^x

P ⁽ s,k x ,k y ) “ 0

Возвращаясь в обычное ( x, y, t ) – представление, получим эффективное уравнение диффузии:

d d1

—

d j a ² a ^1/2 2V D 7 d x ^ a t ⁷⁷²

—

д ² I .

^D 2 ----г| P ⁽ s , k x , k y ) ” ⁰ a y )

Таким образом, получим щенном законе Фика:

операторное выражение для эффективного тензора диффузии в обоб-

^

D eff

I

D 1 d ^1/2

2 V D T d t ^1/2

I         0

D 2 J

В случае трехмерной гребешковой структуры случайное блуждание будет описываться тензором диффузии в следующем виде:

	f Di 5 ( y ) 5 ( z )	0	0
D ij =	0	~ D 2 δ ( z )	0
	V         0	0	1D3 V

Соответственно, получается следующее диффузионное уравнение:

2   22

(— - D i 5 ( y ) 5 ( z )       — D ~ 2 5 ( z )       — D ~ 3 —) G ( x , y , z , t ) = 5 ( x ) 5 ( y ) 5 ( z ) 5 ( t )

5 t                    d x ²              d ² y 5 ² z

Решение трехмерной задачи будем искать в виде, аналогичном (10): ^G (s , k x , y , ^z ) = g (s , k x ^)ex P ^(— ^ y I y I ^{— X} z I ^z l )

Подставляя решение (27) в уравнение (26), определим параметры X y , X z и выражение для функции g(s,k x ):

^{X z} < ^x y

2 D 3 λ z

~

D ₂

g ⁽ s , ^k ) =

~~

2 D ₂ X + D 1 k ²

Сделав преобразования Фурье по координатам y и z, получим функцию Грина для трехмерного слу-

чая

G ( s , k x , k y , k z ) =

4 λ y λ z

(2 D 2 X + D k ²)( X y + k y )(X 2 + k z ²)

Повторяя вышеприведенные рассуждения, получим эффективное уравнения диффузии для трехмер- ного анизотропного случая:

s+

V

----1. ^ s k² + 225 ₂ Uk-k² 2 _1/4 D ~ ₃ D ~ ₂₂ x 2 D ~ ₃ y

+

)

^~ 3 ^kz

P ⁽ s , k x , k y ) » 0

V

Или в обычном представлении:

d d t V

—

D ^~ 1

d

D ₃ D ₂ ² d x

² d ^3/4

;² d t ^3/4

—

2 D ₂ d

d ^1/2

² d t ^1/2

—

_D ~₃

a ² ^

— P ( s , k x , k y ) « 0 a z ²

V

Таким образом, эффективный тензор диффузии в законе Фика для трехмерного анизотропного блуждания на гребешковой структуре имеет вид:

D ˆ eff

~         3/4

_____ ,^D i          ______

2 Vf~71~T^d t ^3,4

^

2 D ~ ₂ 5 ^1/2

~      1/2

_D ~ ₃

V

V

Асимптотические решения обобщенного диффузионного уравнения дробного порядка

Используя формулу (10) и возвращаясь в обычное представление в координатах ( x, y ,t ) получим решение уравнения дробного порядка по времени [25, 26]:

G ( x , y , t ) = J J J J e st e

^{S T} e

2            dk dk e - Dykyт elk^x + ikxy ----x-----ydsd т

2 π             (33)

Однако из полученного формального решения трудно последить пространственное распределение и изменение во времени. Поэтому исследовано асимптотическое поведение в двух предельных случаях: при произвольных Х, t и малых значениях Y; при произвольных Y, t и малых значениях Х, вблизи начала координат. Для исследования асимптотик выполним интегрирование по переменным k x , k y и представим общее решение в виде произведения двух следующих интегралов:

x ²

G ( x , y , t ) = J J dsd т —

xe xτ s 4 2

y ²

4 D yτ e s(t— т)

D y τ

Первый асимптотический предел – при произвольных Х и t и малых значениях Y

Проанализируем первый предельный случай – малые значения координаты Y. Будем искать решение для параметра s в виде разложения: 1) s = s 0 (x) + s 1 (y)

Решение уравнения в исследуемом приближении и главном порядке s 0 (x) имеет вид:

x ³

• ⁵ 0 = ^A 4/

• ^{t 3} здесь А постоянная величина.

Следующее приближение s 1 (y) описывается выражением:

5 = y

¹    8 D_yt ²

Таким образом, в полученном приближении

Здесь константа

/

X

G ( x, y, t ) * exp J

C =

Cx ³

2 ^y

8 D_yt

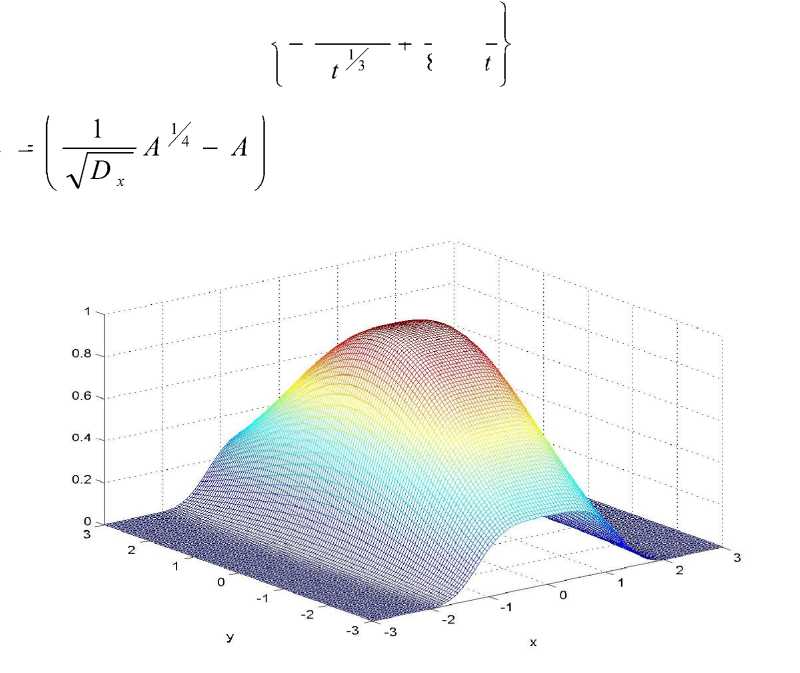
Рис. 1. Плотность распределения диффундирующих частиц на плоскости (x, y) в пределе малых значений Y

В главном порядке

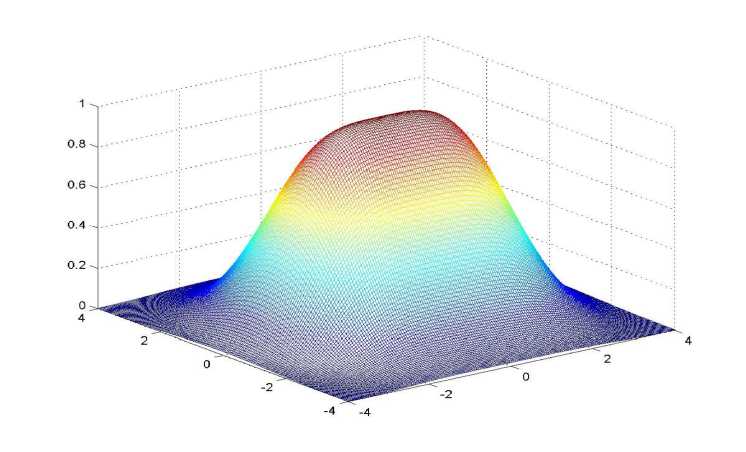
Рис. 2. Плотность распределения диффундирующих частиц на плоскости (x, y) в пределе малых значений Х

Полученное асимптотическое решение имеет необычное, отличное от гауссового поведение по координате Х. Второй асимптотический предел – при произвольных Y и t и малых значениях Х. В этом предельном случае искать решение для параметра s в другом виде s = s0(y) + s1(x) + s2(x, y);

^ 0 ⁽ У ) = 4^

Первый порядок по координате X равен нулю, в следующем приближении получим:

= x4 Dy s2 64Dx2y2

Следовательно, решение в этом асимптотическом пределе имеет вид:

y ²

G ( x , y , t ) ^

e ⁴ Dyt

x ⁴ D_yt

4 π D y t

e 64 Dx ² y ²

Полученное асимптотическое решение в этом пределе имеет гауссовое поведение по координате У. Дополнительный малый множитель, описывающий поведение при малых значениях координаты Х появляется только во втором приближении.

Заключение

Таким образом, показано, что аномальное случайное блуждание на многомерной гребешковой структуре в асимптотическом пределе больших времен (больших масштабов) описывается эффективными диффузионными уравнениями, содержащие помимо обычных пространственных производных также и производные по времени дробного порядка. Иными словами, эффективный тензор диффузии в законе Фика приобретает операторный вид – формулы (22) и (29), при этом степень дробной производной по времени разная для различных направлений. Такое необычное представление связано с аномальным субдиффузионным характером случайных блужданий на многомерной гребешковой структуре. По-видимому, такое операторное представление для тензора диффузии в случае анизотропных аномальных случайных блужданий получено впервые.

Полученные результаты будут полезны и при исследовании процессов тепло-массопереноса в пористых средах. В современной электронике все чаще применяют металл с низким сопротивлением (Cu вместо Al) и диэлектрики с низким значением диэлектрической проницаемости – low k диэлектрики вместо традиционного SiO 2 . Такие диэлектрики, как правило, имеют пористую наноструктуру, наиболее желательное предельное значение диэлектрической проницаемости этих диэлектриков является проницаемость вакуума, равная 1. Развитый выше подход на основе обобщенных диффузионных уравнений дробного порядка и полученные результаты также могут быть применены и для исследования диффузии активных частиц в пористых материалах с низкой диэлектрической проницаемостью, которые и ответственны за технологические повреждения в этих материалах [27, 28].