Эффективные дискретные ортогональные преобразования в компрессии цифровых аудиоданных

Работа посвящена обоснованию класса дискретных ортогональных преобразований (ДОП), наиболее перспективного для целей высокоэффективной и высококачественной компрессии цифровых аудиоданных. Вырабатываются требования, которым должны удовлетворять такие ДОП и проводится соответствующий анализ наиболее известных из них.

Постановка задачи

В современных стандартизованных цифровых технологиях обработки и передачи звуковых сигналов (ЗС) используются дискретные косинусное преобразование (ДКП) и преобразование Фурье

(ДПФ). Однако скорость цифрового потока на выходе соответствующих кодеков при том же качестве субъективного восприятия восстановленного звука практически одинакова. Вследствие этого всегда остаются сомнения относительно превосходства класса гармонических ДОП над другими классами преобразований. Эти сомнения подкрепляются отсутствием обоснованных требований, которым должны удовлетворять ДОП, потенциально способные обеспечить наиболее эффективную компрессию цифровых аудиоданных при сохранении высокого качества субъективного восприятия звука.

В статье на основе известных психоакустических свойств слуха вырабатываются указанные требования, и проводится соответствующий анализ наиболее известных классов ДОП.

Требования к ДОП в высококачественных системах сжатия ЗС

Одним из органов слухового аппарата, воспринимающего звуковые колебания, является базилярная пластинка, представляющая собой порядка 20000 слуховых струн разной длины и толщины, реагирующих на колебания различной частоты. Распределение амплитуд колебаний различной частоты вдоль базилярной пластинки при уровне звукового давления 1 мкб представлено на рис. 1 [1]. Видно, что тон, воздействуя на базилярную пластинку, возбуждает определенный участок ее струн. На этом основании естественно потребовать, чтобы ДОП допускало интерпретацию своих коэффициентов как узкополосного шума. С другой стороны, наибольшее колебание получает струна, «настроенная» на частоту этого тона. Как оказалось [2] колебание именно этой струны переводится в ощущение. Таким образом, слуховому анализатору характерен эффект маскировки – подавление более интенсивным тоном соседних менее интенсивных тонов. Эффект маскировки позволяет допустить, что слуховой анализатор непрерывно обрабатывает линейчатый спектр и, следовательно потребовать от ДОП возможности интерпретации его коэффициентов как тональных компонент.

Рис. 1. Зависимость амплитуд колебаний базилярной пластинки от расстояния до овального окна

Обе интерпретации не противоречат друг другу. Действительно, с точки зрения электроакустики распределение интенсивности узкополосного шума совершенно безразлично [3]. Она может быть распределена равномерно или в любой его области, даже в одной спектральной компоненте. Экспериментально установлено [2], что слух менее чувствителен к изменениям уровня шума, чем тона. Это предполагает эффективную реализацию усечения коэффициентов ДОП – передачу не всех, а лишь части разрядов их цифрового представления. Таким образом, сочетание описанных интерпретаций позволяет оценить распределение допустимой степени усечения спектральных компонент в пределах интервала преобразования, а также эффективно реализовать эффект маскировки – передачу только немаскируемых коэффициентов ДОП.

Эффект маскировки исследован достаточно полно [2]. Результаты измерения таких порогов слышимости тона при маскировке узкополосным шумом со средней частотой 1 кГц, шириной полосы 160 Гц и уровнем 100, 80, 60, 40 и 20 дБ приведены на рис. 2.

Видно, что при определенных условиях эффект маскировки распространяется почти на весь слышимый диапазон частот. На этом основании можно сделать вывод, что ДОП должно обеспечивать глобальную декорреляцию отсчетов ЗС. Что касается полноты декорреляции, достаточно потребовать, чтобы ширина полосного шума не превышала частотного разрешения используемого преобразования. В этом случае декорреляцию вполне можно считать полной.

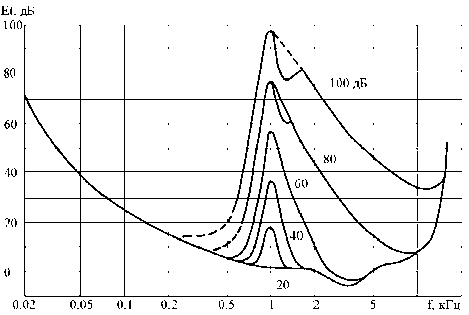
Рис. 2. Кривые порога слышимости тона при маскировке узкополосным шумом

Многие современные системы цифровой обработки звуковых сигналов работают в режиме реального времени. В связи с этим ДОП должны обладать быстрыми вычислительными алгоритмами.

Таким образом, ДОП можно считать перспективным для целей компрессии цифровых аудиоданных, если оно отвечает следующим требованиям:

• -    обладает быстрым вычислительным алгоритмом;

• -    естественным образом допускает интерпретацию своих коэффициентов как тональных компонент ЗС;

• -    допускает интерпретацию каждого коэффициента как центральной компоненты узкополосного шума, в которой сконцентрирована его интенсивность;

• -    обеспечивает глобальную декорреляцию отсчетов ЗС.

Анализ ДОП

Наибольшая эффективность сжатия цифровых аудиоданных можно ожидать при использовании преобразования Карунена-Лоэва, или дискретного преобразования Хотеллинга, коэффициенты которого полностью некоррелированны. По отношению к критерию среднеквадратичной ошибки оно является оптимальным для представления сигналов. Однако это справедливо для стационарных процессов, когда разложение Карунена-Лоэва производится по собственным функциям интегрального уравнения Фредгольма с ядром, равным корреляционной функции процесса. Применительно к ЗС на интервалах, меньших интервала стационарности, данное разложение можно использовать, но для каждого такого интервала придется строить свой базис по его корреляционной функции. Кроме того, не существует общего быстрого алгоритма для вычисления преобразования Карунена-Лоэва или его обратного преобразования. Поэтому на практике используют субоптимальные преобразования.

Субоптимальные преобразования можно разделить на две группы – негармонические и гармонические. Начнем с негармонических преобразований.

Базисные функции преобразования Уолша-Адамара представляют собой дискретные функции Уолша [4], которые можно выразить с помощью матриц Адамара. Преобразование имеет быстрые вычислительные алгоритмы, обеспечивает глобальную декорреляцию исходных данных и позволяет оценить энергетический спектр последовательности данных. Вместе с тем функции Уолша состоят из прямоугольных волн, что, во-первых, делает весьма затруднительным использование в целях сжатия ЗС психоакустических свойств слуха. Во-вторых, обусловливает зависимость номера коэффициента преобразования от числа пересечений соответствующей гармоникой нулевого уровня. Действительно, при интервале преобразования длительностью Т п и частоте гармоники не превышающей 1/(2 - Т _п ) может не оказаться ни одного пересечения. В результате в низкочастотной области с большой вероятностью возможны потери информации.

Базисные функции преобразования Хаара представляют собой матрицы Хаара размером N x N, каждая из которых получается в результате дискретизации системы функций Хаара [5]. Преобразование имеет быстрые вычислительные алгоритмы, но глобальная декорреляция обеспечивается только двумя первыми коэффициентами. Из остальных N /2 коэффициентов соответствуют корреляции двух соседних точек в пространстве входных последовательностей, N /4 коэффициентов – четырех соседних точек и т.д. В результате решение вопроса об энергетическом спектре входных последовательностей крайне затруднительно.

Хорошие средства для частотно-временного анализа нестационарных сигналов предоставляет вейвлет-преобразование [6]. Здесь в качестве весовых коэффициентов сигнала выступают вей-влетные функции. Все они получаются из какой-либо основной (материнской, базовой) вейвлет-ной функции и характеризуются следующими свойствами:

• -    имеют вид коротких, локализованных во времени (или в пространстве), волновых пакетов (вейвлетов) с нулевым средним;

• -    обладают возможностью сдвига по времени; способны к масштабированию (сжатию или растяжению);

• -    имеют ограниченный (или локальный, полосовой) частотный спектр.

Однако почти все вейвлеты не имеют аналитического представления в виде одной формулы и задаются итерационными выражениями. Кроме того, число вейвлетов, используемых при разложении сигнала, задает уровень его декомпозиции. При этом за нулевой (высший) уровень декомпозиции принимается сам сигнал. Точность же представления сигнала по мере перехода на более низкие уровни декомпозиции снижается. Следовательно, применительно к сжатию ЗС вейвлеты целесообразно использовать для реализации банка фильтров в методе полосного деления с ортогональным преобразованием.

Таким образом, с большой долей уверенности можно утверждать, что негармонические ДОП не способны обеспечить предельную эффективность сжатия цифровых аудиоданных.

Более перспективными являются гармонические ДОП, поскольку в той или иной степени удовлетворяют всем сформулированным выше требованиям. Из них наиболее известными являются дискретные преобразования Фурье (ДПФ), Хартли (ДПХ) и косинусное преобразование (ДКП).

Прямое и обратное ДПФ может быть определено для конечной последовательности { х ( п )}" 01 действительных или комплексных чисел [7]. Каждый коэффициент преобразования является функцией всех отсчетов ЗС данной выборки. Следовательно, ДПФ обеспечивает глобальную декорреляцию. Кроме того, известно, что ДПФ представляет собой дискретные отсчеты спектральной функции дискретного сигнала. По этой причине коэффициенты ДПФ называют спектральными отсчетами с амплитудой Y F (k) и фазовым сдвигом W_F(k). Рассмотрим АЧХ к -го коэффициента ДПФ (см. рис. 3). Видно, что, во-первых, корреляция между спектральными компонентами незначительна, поскольку обусловлена только пересечением лепестков их АЧХ. Во-вторых, коэффициенты концентрируют в себе энергию некоторой полосы, величину которой можно определить равной частотному расстоянию между ними.

Для ДПФ известны быстрые вычислительные алгоритмы, обеспечивающие в наилучшем случае выполнение 0,5 N log 2 N арифметических операций.

плоскости вещественной переменной. Эти преобразования связаны взаимно однозначными соотношениями, базирующимися на свойстве симметрии. Отсюда амплитудный и фазовый спектры ДПХ вычисляются подобно ДПФ:

Y H (k) = 1

7 [ C h (k )]²

( C ( k ),

^; ( k ) = 1

arctg

⎩ 0,

+ [ C h ( N - k )] 2

/2,k = 1 ... N - 1, k = 0,

C h ( N - k ) - C h ( k )

C h ( N - k ) ₊ C h ( k )

, k = 1 ... N - 1,

k = 0.

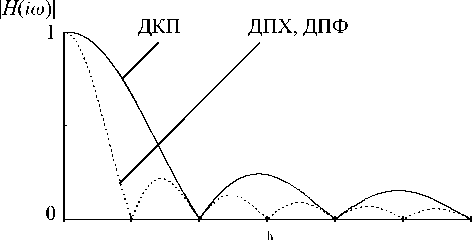
Рис. 3. АЧХ k -го коэффициента гармонических ДОП

АЧХ k -го коэффициента ДПХ (см. рис. 3) такое же, как и для ДПФ. В этом случае, так же справедлива интерпретация коэффициентов как узкополосного шума шириной полосы равной частотному разрешению ДПХ. Данное преобразование имеет быстрые вычислительные алгоритмы, при этом отсутствие комплексной арифметики значительно сокращает объем вычислений по сравнению с быстрыми алгоритмами вычисления ДПФ, так как одно комплексное умножение эквивалентно четырем операциям действительного умножения и двум операциям сложения. Следует также отметить, что в отличие от ДПФ прямое и обратное ДПХ взаимно симметричны. Это позволяет использовать для их выполнения одни и те же программы и одну и ту же аппаратуру.

Прямое и обратное ДКП вещественной последовательности { _x ( n )} N ¹ определяется, соответственно, как [9]:

N ¹

E 2 n + 1     ⁽³⁾

x(n) •          k

V 2 N )

n = 0

Прямое и обратное ДПХ последовательности {x(n)}_{n = 0} конечных действительных чисел определяется, соответственно, парой формул [8]:

2 n+1

Xc (n) = L A(k)-C (k)• c 2—12

k = 0

C ( к )

H

N

N ~1                  /           \

Е 2 * x ( n )-cas         n ,

N n - 0

где k ; n = 0; 1; … N – 1, C_C ( k ) – k -ый коэффициент ДКП, а нормировочный коэффициент X(k) вычисляется по формуле:

N ^- 1

E 2 n

CH (k)-casl "^k I’ k = 0

1/ V N при k = 0,

. 4T)N при к = 1;2... N- 1.

где C_H ( k ) – k -ый коэффициент ДПХ, а cas(x) = cos(x) + sin(x) - ядро преобразования является вещественным, k; n = 0; 1 ... N - 1.

Из выражений (1)-(2) видно, что ДПХ обеспечивает глобальную декорреляцию. Кроме того, ДПХ представляет собой модификацию ДПФ в

Из (3)-(4) видно, что ДКП также обеспечивает глобальную декореляцию ДКП исходного массива данных равно действительной части ДПФ того же массива, взвешенной частотнозависимым окном:

wk(n) = X(k)-exp[znk(n - 0,5)/N].

Совокупность весовых функций w_k ( n ) позволяет уменьшить влияние краевых эффектов, возникающих за счет несовпадения амплитуды сигнала в начале обрабатываемой выборки и в конце при использовании ДПФ с естественным временным окном.В то же время система весовых функций подобрана так,что базисные функции ДПФ, взвешенные этим окном, образуют новую систему ортогональных функций – базис ДКП. Следовательно, во-первых, гарантируется отсутствие эффекта увеличения ошибок кодирования при обратном ДКП. Во-вторых, коэффициенты ДКП можно интерпретировать как спектральные отсчеты. В-третьих, можно вычислить C_С(k) с помощью 2 N -точечного алгоритма быстрого преобразования Фурье. Известно так же, что базисные векторы ДКП очень хорошо аппроксимируют собственные векторы теплицевых матриц. Это свойство позволяет рассчитывать на эффективное использование ДКП в области сжатия сигналов.

Как видно по АЧХ (см. рис. 3) коэффициенты ДКП можно интерпретировать как полосный шум с энергией, определяемой величиной соответствующего коэффициента и шириной равной частотному расстоянию этого преобразования. При этом корреляция соседних коэффициентов значительна. Однако эту проблему можно решить, если обрабатывать отдельно четные и отдельно нечетные коэффициенты преобразования.

Выводы

Сформулированы обоснованные требования, позволяющие установить наиболее перспективный класс ДОП в задачах высокоэффективной и высококачественной компрессии цифровых аудиоданных. Для целей сжатия цифровых звуковых сигналов наиболее перспективными являются ДПХ и ДКП, потенциально способные обеспечить ее максимальную эффективность.