Эффективные и простые в изготовлении интегральные плазмонные решётки для телекоммуникационного оптического диапазона

К интегральной фотонике в последнее время проявляют большой интерес, в том числе благодаря возможностям изготовления оптических компонентов высокой плотности на компактном чипе. Кремниевая технология позволяет изготавливать разнообразные пассивные фотонные компоненты с микронными и с субмикронными размерами, однако активная элементная база пока находится на стадии разработок.

Интегральные оптические модуляторы, работающие на эффекте плазменной дисперсии в кремнии, имеют длину около миллиметра, занимая значительную часть чипа [1]. Несмотря на неплохие характеристики таких модуляторов, их относительно большие размеры создают трудности для многих практических применений. Гибридные плазмонные волноводы способны сильно локализовать моду и обеспечить высокую глубину модуляции оптического сигнала при воздействии на активную область с электрооптическим материалом, с относительно малыми характерными размерами [2, 3].

Кроме задач модуляции оптического сигнала в интегральной фотонике, плазмонные волноводные моды могут представлять интерес в задачах измерения показателя преломления различных веществ [4] и в микрофлюидных биосенсорах [5].

Плазмон-поляритонные моды на границе раздела металл–диэлектрик возбуждаются с помощью наноантенн [6], призмы в схеме Кречмана [7] или сформированных на металлической плёнке дифракционных решёток [3, 8, 9]. Решётки соединяются металлическим волноводом. При помощи оптического волокна излучение с p - поляризацией направляется на решётку ввода под определенным углом к плоскости чипа. Плоскость падения излучения перпендикулярна зубцам решётки. Решетка перенаправляет излучение вдоль поверхности металла, возбуждая поверхностную плазмонную моду. Решётка вывода перенаправляет оптическое излучение на детектор.

Эффективность решётки ввода – это отношение мощности волноводной моды к мощности источника излучения, падающего на решётку. Эффективность решетки вывода – это отношение мощности на выходе из решетки к мощности волноводной моды. В условиях эксперимента эффективность ввода /вывода считается 1/2 от измеренного отношения мощности на выходе к мощности на входе [10]. Потери в волноводе вычитаются.

В отличие от экспериментов с решётками в диапазоне длин волн 700–800 нм [11 – 13], наше исследование ориентировано на разработку плазмонных структур для телекоммуникационного оптического диапазона. На сегодняшний день самая эффективная плазмонная решётка, работающая в телекоммуникационном диапазоне, продемонстрирована в работе [8]. Решётки, описанные в работе [8], сложны в изготовлении, поскольку включают в себя двухуровневые зубцы, которые требуют две точно совмещенных литографии с высоким разрешением и два этапа травления. В работе [8] также исследована аподизированная геометрия плазмонной решётки, полученная в результате работы алгоритма оптимизации. Для определения эффективности решётки из общего пропускания системы были вычтены потери оптоволоконной и измерительной части. Также вычитались потери распространяющейся плазмонной моды на длине 20 мкм между решетками. В результате были достигнуты эффективности ввода /вывода излучения – 3,5 дБ и –2,9 дБ для равномерной и аподизированной решёток соответственно. Авторы использовали полиметилметакрилат в качестве диэлектрика, в котором сосредоточена основная часть интенсивности электромагнитного поля плазмонной моды.

В данной работе разрабатывалась равномерная плазмонная дифракционная решётка, сформированная на границе золота и тетраэтилортосиликата (ТЭОС). Процесс изготовления решётки включал один процесс литографии и один травления. Описанные здесь решётки более технологичны, то есть менее требовательны к точности литографии и потенциально могут быть изготовлены быстрее, чем структуры из статьи [8]. Для изготовления структур была разработана технология формирования золотых плазмонных решёток без использования плазмохимического травления золота. Для структурирования слоя золота на стадии перед осаждением металла применялся процесс травления подложки кремния.

В статье приведены данные численного моделирования, на основании которых разработан дизайн плазмонных решёток, описан маршрут изготовления, а также представлены результаты экспериментального тестирования структур при помощи пары линзованных оптических зондов. Длина волноводов для всех изготовленных структур составила от 150 до 250 мкм. Продемонстрирована эффективность – 3,8±0,2 дБ на одну решётку. Измеренные оптические потери на распространение плазмон-поляритонной моды составили 0,14 ± 0,02 дБ /мкм.

1.    Моделирование

Плазмонная решётка представляет собой последовательность параллельных штрихов в слое золота, которые чередуются с периодом Λ . Схематично послойная структура плазмонной решётки изображена на рис. 1.

Как показано ранее в работах [10, 14], условие Брэгга–Вульфа для первого порядка дифракции (1) и выражение, аппроксимирующее эффективный индекс плазмонной моды в области решётки (2), дают хоро- шие стартовые геометрические параметры дифракционных решёток для последующей оптимизации численными методами.

Х = л ( H f - П а sin ( 9 ) ) ,                           (1)

ne ff = ffn 0 + ( 1 - ff ) n e .                                (2)

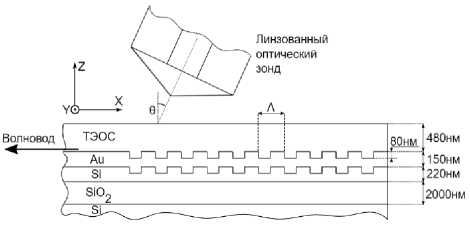
Рис. 1. Схематичное изображение сечения плазмонной решётки. Стрелка на рисунке указывает направление в сторону интегрального плазмонного волновода

Эффективный индекс плазмонной моды решётки n eff можно аппроксимировать в соответствии с (2) как средневзвешенное значение индексов поверхностных плазмонных мод на плоской границе золото / ТЭОС с s ( z ) зубца для n o и штриха для n_e . Период и заполнение решётки обозначены Л и // соответственно. Показатель преломления среды, в которой расположены зонды, – n a . В нашем случае для воздуха n a = 1. Угол наклона зондов к нормали θ = 14,4 градусов.

В нашем случае рассчитанные при помощи программного пакета Comsol Multiphysics Wave Optics эффективные индексы плазмонных мод n 0 и n e составили 1,360 и 1,385. Интенсивность электрического поля этих мод в зависимости от перпендикулярной чипу координаты изображена на рис. 2. Максимумы интенсивности электрического поля с координатами 70 нм и 150 нм соответствуют верхней границе золота. Максимумы интенсивности электрического поля с координатой 630 нм соответствуют границе между ТЭОСом и воздухом.

Благодаря численной оптимизации решётки под стыковку с зондом, расположенным под углом к чипу, решётка не создаёт резонансные условия для волноводной плазмонной моды. Из-за этого переотраже-ния между решёткой и волноводом оказываются незначительными.

Из формул (1, 2) можно найти период решётки. Подразумевая // = 0,5, период Л =1379 нм для центральной длины волны λ = 1550 нм.

Аналитическая оценка давала стартовые параметры для оптимизации структуры при помощи численного моделирования плазмонной решётки ввода излучения. Моделирование проводилось с использованием двумерного метода конечных разностей во временной области в программном пакете Comsol Multiphysics Wave Optics. Различия между двумерным и трёхмерным методами для решёток ввода /вывода малы, поэтому многие исследователи ограничиваются двумерным методом [14]. Для оптимизации был использован алгоритм Нельдера–Мида, реализованный в библиотеке SciPy для языка программирования Python. В качестве целевой функции использовалась мощность плазмонной моды на длине волны 1550 нм в точке, удалённой от решётки ввода на 20 мкм по направлению распространения плазмонной моды. Мощность плазмонной моды считалась как усреднённый по времени интеграл проекции вектора Пойн-тинга, перпендикулярной линейному детектору от z =–2 мкм до z =3 мкм.

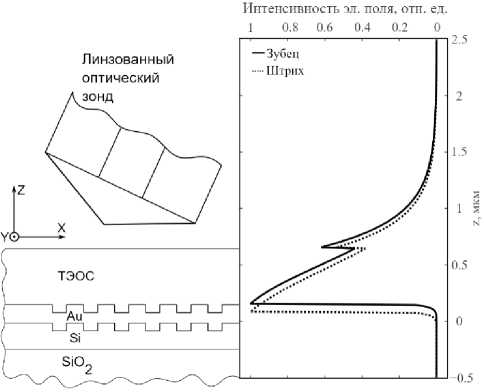
Рис. 2. Справа: рассчитанное распределение интенсивности электрического поля поверхностных плазмонных мод для ε (z) зубца (сплошная линия) и штриха (пунктирная линия). Слева: схематичное изображение сечения плазмонной решётки с соблюдением масштаба по оси z

В результате оптимизации были получены следующие параметры решётки: ƒƒ = 0,55; Λ = 1293 нм. Глубина травления 80 нм не участвовала в оптимизации. Распределение интенсивности электромагнитного поля, полученное для структуры с оптимизированными параметрами, изображено на рис. 3.

X, мкм

Рис. 3. Рассчитанная интенсивность электромагнитного поля, характерная для решётки ввода

Излучение на выходе линзованного оптического зонда имеет диаметр моды 7 мкм в окрестности фокальной плоскости. Поэтому излучение источника моделировалось в виде Гауссова пучка с перетяжкой, диаметр которой равен 7 мкм по уровню интенсивности 1/e2. Высота расположения источника излучения над поверхностью золота, а также расстояние до перетяжки –10 мкм. В расчёте использована сетка 50 нм по оси x и 10 нм по оси z. Моделирование происходило с длиной волны источника 1550 нм, и пар-раллельной оси y поляризацией. Оптимальное положение источника по оси x установлено перебором координат источника в окрестностях 20 мкм вокруг координаты первого штриха.

Для длины волны 1550 нм пиковая расчётная эффективность решётки ввода составила –3,4 дБ. Эффективность вычислялась как отношение мощности плазмонной моды в точке x =–20 мкм к мощности источника. Далее полученное значение увеличивалось на долю, которая соответствует затуханию плазмонной моды на расстоянии 20 мкм между первым штрихом и точкой измерения мощности.

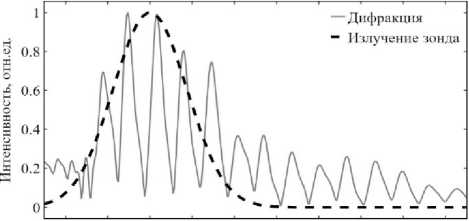
Согласование дифракционной моды решётки с модой излучения зонда является одним из основных факторов, влияющих на эффективность связи плазмонного волновода и линзованного волокна. Для того, чтобы оценить, насколько хорошо согласуются моды решётки и волновода, обычно используют распределение интенсивности над решёткой вывода [14]. Проанализировав рассчитанную интенсивность излучения дифракции на высоте 0,85 мкм над решёткой вывода с оптимизированными параметрами, изображённую на рис. 4, можно заметить, что форма огибающей интенсивности дифрагировавшего излучения близка к интенсивности излучения использованных нами волоконных линзованных зондов.

О 2     4     6     8     10    12    14    16

X, мкм

Рис. 4. Интенсивность излучения линзованного зонда (чёрная пунктирная линия) и интенсивность дифракционного излучения над решёткой вывода на высоте 0,85 мкм (серая сплошная линия)

В соответствии с [10, 14] согласование интенсивностей дифракционной моды решетки и излучательной моды зондов необходимо для достижения эффективной связи волокна и волновода на чипе. Расчётный результат, изображенный на рис. 4, демонстрирует согласованность мод решётки и зонда, что объясняет высокую рассчитанную эффективность решёток.

2.    Изготовление

Металлические плазмонные решётки с параметрами, полученными в оптимизации, и волновод изго- тавливались на подложке кремний-на-изоляторе. Структурирование подложки осуществлялось с помощью метода электронно-лучевой литографии на установке сканирующей электронной микроскопии JEOL JSM-7200F c литографической приставкой Xenos XPG 2. Схема вертикального разреза структур представлена на рис. 1. Плазмохимическое травление кремния на глубину 80 нм проводилось через маску электронно-лучевого резиста AR-P 6200 series (CSAR 62) в установке PlasmaPro100 (Oxford Instruments). После удаления маски резиста на подложку осаждался слой золота (чистота 99,999 %) толщиной 150 нм методом электронно-лучевого осаждения (Angstrom Nexdep, Angstrom Engineering). После осаждения в пленке золота формировался необходимый рельеф, определяемый морфологией нижележащего кремниевого слоя.

Для формирования планарной структуры решёток и волноводов слой резиста вместе с осаждённым на него золотом удалялся в диметилформамиде. Процесс удаления резиста проводился при температуре 60° C в течение десяти минут. Ширина золотого волновода, соединяющего плазмонные решётки, равна 7 мкм, а его длина варьировалась в диапазоне 150–250 мкм. Ширина волновода выбиралась исходя из размера пятна излучательной моды линзованного зонда так, чтобы способствовать согласованию этой моды и плазмонной моды волновода. На рис. 5 представлено изображение структуры, полученное на сканирующем электронном микроскопе.

Рис. 5. Изображение фрагмента плазмонной решётки и волновода. На изображениях более светлый оттенок соответствует золоту, а более тёмный – кремнию

После осаждения золота на чип был нанесён слой ТЭОСа высотой 650 нм. Материал был получен на основе гидролиза и конденсации тетраэтилортосиликата с использованием соляной кислоты в качестве катализатора в присутствии деионизованной воды. Готовый гель перед нанесением был разбавлен этанолом в соотношении 1:1 для понижения вязкости и получения слоев нужной толщины.

Нанесение на образец осуществлялось в два этапа центрифугированием со скоростью 8000 об /мин. в течение 15 минут. После нанесения каждого из двух слоев проводился плавный нагрев с последующим отжигом при температуре 250 ° C. Толщина после нанесения измерялась методом эллипсометрии и оказалась равной 650 нм, а показатель преломления на длине волны 1550 нм составил 1,42. Впоследствии произошла усадка ТЭОСа до толщины 630 нм, а показатель преломления оказался равным 1,43.

3.    Оптическая характеризация

На чипе было изготовлено 18 пар плазмонных решёток с соединяющим их волноводом. Для того, чтобы измерить оптическое пропускание структур, использовалась зондовая станция MPS150 (Cascade Microtech), пара линзованных зондов LWP (Cascade Microtech) и анализатор оптического спектра BOSA 400 (Aragon Photonics). Перестраиваемый источник излучения был подключен при помощи оптического волокна типа Panda с сохранением поляризации к оптическому зонду, который наводился на плазмонную решётку. Излучение, испускаемое другой плазмонной решёткой на противоположной стороне волновода, собиралось другим оптическим линзованным зондом. Излучение, собранное этим зондом, перенаправлялось на вход оптического анализатора спектра при помощи оптического волокна типа Panda с сохранением поляризации. Угол наклона зондов был установлен в соответствии с расчётным значением 14,4 ± 0,3°.

Для корректной оценки пропускания структур была произведена оценка потерь в системе. Для этого измерялось пропускание системы, в которой оптические зонды нацелены не на решётки, а друг на друга. Зонды были размещены на расстоянии, при котором пропускание излучения оказывается наибольшим. Пропускание в системе, измеренное таким образом, оказалось –4,0 дБ. Пропускание референсной системы практически не зависит от длины волны (разброс значений в пределах –4,2–4,0 дБ) в диапазоне длин волн 1520 – 1630 нм.

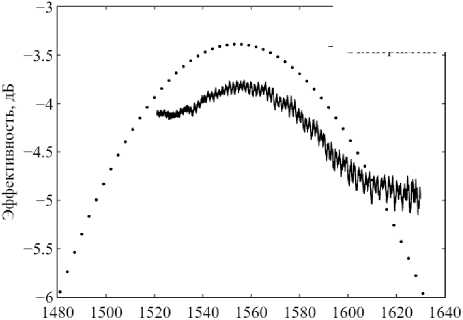
В результате измерений были получены спектры пропускания интегральных плазмонных структур. Спектр с наиболее высоким измеренным значением пропускания изображен на рис. 6. Также на рис. 6 изображен рассчитанный спектр пропускания оптимизированной решётки ввода.

Потери плазмонной моды на распространение по поверхности золотого волновода можно определить по формуле а = (Tk- Tn)/(lk-ln), где Tk и Tn - это пропускания плазмонных структур (решётка–волновод– решётка) в логарифмическом масштабе, а lk и ln – их длины. Для оценки затухания плазмонной моды мы усредняли значения а для следующих пар (lk, ln), выраженных в микрометрах: (250, 200); (200, 150); (250, 150). Пропускания Tk и Tn соответствовали структурам с длинами lk и ln. Усреднённые потери плазмонной моды для используемых в эксперименте длин оказались 0,14 ± 0,02 дБ /мкм. Если вычесть из пропускания структуры затухания моды на её длине, результатом окажется удвоенная эффективность плазмонной решетки. Вычисленная таким образом эффективность составила –3,8±0,2 дБ.

• Симуляция — Эксперимент

Длина волны, нм

Рис. 6. Спектр пропускания решётки ввода, полученный в численных расчётах (точки) и в эксперименте (сплошная линия)

Заключение

Используя условие Брэгга–Вульфа, линейную аппроксимацию эффективного индекса моды в области решётки, численный расчёт и алгоритм оптимизации Нельдера–Мида, определены параметры золотой структуры, подходящие для эффективной связи плазмонного волновода и оптического волокна. При помощи метода конечных разностей во временной области было вычислено распределение интенсивности электромагнитного излучения, характерное для решётки ввода. Расчёт показал предельную эффективность решётки –3,4 дБ.

Мы использовали ТЭОС в качестве покрывающего материала для изготовленных решёток и волноводов. ТЭОС устойчив к ацетону и диметилформамиду, и поэтому удобней для дальнейшего использования чипа, чем полиметилметакрилат, применённый в качестве покрывающего слоя, например, в [8]. Благодаря использованию ТЭОСа, плазмонная мода была локализована вблизи поверхности металла в слое толщиной 480 нм (на полувысоте интенсивности электромагнитного поля). Измеренные потери этой моды составили 0,14 ± 0,02 дБ /мкм.

Разработанная дифракционная решётка позволила эффективно перенаправлять оптическое излучение диапазона 1520–1630 нм в плазмонную моду на границе золото / ТЭОС. Измеренная эффективность решётки составила –3,8±0,2 дБ. Экспериментально полученные значения эффективности близки к теоретически предсказанным значениям, представленным на рис. 6.

Разработанный дизайн решёток ввода /вывода позволил достичь высокой эффективности при помощи простой в изготовлении структуры. В отличие от дизайна из статьи [8], наш подход требует всего одну литографию и одно травление для изготовления рельефа решёток. Такой дизайн исключает необходимость точного совмещения литографий. Характерные размеры нашей структуры менее требовательны к точности литографии по сравнению с дизайном [8].

Дифракционная мода решётки зависит от периода, заполнения и контраста показателей преломления зубца и штриха [15]. Сходство огибающей интенсивности дифрагировавшего излучения с распределением интенсивности излучения линзованного зонда (см. рис. 4) подтверждает, что найденные нами параметры решётки обеспечивают согласование мод, и, как следствие, приводит к высокой измеренной эффективности структур.