Эффективные модули объемного сжатия дисперсно-упрочненных композитов со сплошными и полыми анизотропными сферическими включениями

Рассмотрим двухфазный композит, армированный сплошными или полыми сферическими включениями различного диаметра. Придерживаясь гипотез полидисперсных моделей механики [1], будем считать, что каждая сферическая частица произвольного радиуса R a окружена слоем связующего толщиной R b - R a таким образом, что отношения c = Ra/R b для каждого армирующего элемента и h = Rq] R ^ для каждого полого включения являются постоянными величинами. Кроме того, будем предполагать, что линейно упругая однородная матрица изотропна, а материал, из которого изготовлены включения, - сферически трансверсально-изотропный (ось симметрии бесконечного порядка совпадает с осью r сферической ортогональной системы координат r , 0 и ф с началом в центре составной частицы.

Рассмотрим произвольное включение с неизменным типом упругой симметрии составных частей (частицы армирующего наполнителя и слоя матрицы), находящееся в состоянии однородного гидростатиче- ского растяжения, которое обеспечивается заданными на внешней поверхности равномерно распределенными радиальным давлением р

°rrl r=RB = Р, или перемещением ф ur r=RB = 4.                             (2)

Используя точные аналитические решения задач Ламе о равновесии толстостенных трансверсально-изотропных [2] и изотропных сфер [3], запишем выражения для радиальных перемещений u _r и напряжений о _rr в полом включении и окружающем слое матрицы:

_иⁱ₌ Apn I² | B I          ₌ 1 ^f у ” - 3²        B I^H 2 )

ur Air     + n+12 , ° rr Jr     AiH1 n +3/2 I ,(3)

r '                2 V

Hi = An (2 n -1) + 4 A12, H 2 = An ( 2 n +1)-4 A12, uM = AMr + B^, °M = 3KMAM -4GMBM,(4)

r2

где K _M и G _M - объемный и сдвиговой упругие модули. Здесь и далее все величины, относящиеся к включениям и матрице, будут отмечены индексами I и M соответственно.

Для дисперсно-упрочненного композита со сплошными включениями в уравнениях (3) исключаются слагаемые с B_i , наличие которых в решении приведет к сингулярности радиальных перемещений и напряжений в центре частиц армирующего наполнителя:

I u _r

= C I r n ^{- 12},

i ₌i C i H 1 ° ^rr   _{2 r} 3/2 - n "

Содержащийся в равенствах (3) и (5) показатель анизотропии n =   1 + 2 A22 + A23 - A12

4           A ₁₁

определяется модулями Юнга E i , E i и коэффициентами Пуассона и i и и i материала включений:

л _ Ei ^{( 1 -и} i ⁾     Д _!°1 ° i

A ¹¹ =     _F ’   A ¹² = F ’

a2 2 =--E1—-

22 F (1 + и i)

¹ -° ²'E6 , V      E i )

A 23 -

E I

F (1 + 6 i R

-1 E,) 6 I + u iV , El)

F - 1 -и,- 2 6 2 E I .

I     I _{E I}

Рассмотрим наиболее простой случай, когда на межфазной поверхности выполняются условия идеального контакта urI

- uM\ r - RA r

^, r = RA

^O rr

M n O rr r - RA

^{r -} RA ’

а внутренняя поверхность полых сферических включений свободна от напряжений:

O 4 r - R 0 - °-                          (7)

Тогда из решения системы линейных алгебраических уравнений, которая получается при подстановке (4) и (5) в равенства (1) и условия (6), могут быть однозначно вычислены константы интегрирования:

С , - 2 H e ( 4 G_M + 3 K_M ) R A²"n , A_M - H e ( H , + 8G m ) ,

Bm --(H1 - 6Km)HeRA.

He - P [GM (H1 - 6Km ) c3 + 3Km (H1 + G )Г • если композит армирован сплошными сферическими включениями. В случае, когда включения являются полыми, подстановка (3) и (4) в выражения (1) и условия (6) и (7) позволяет записать систему алгебраических уравнений и решить ее относительно неизвестных постоянных интегрирования:

A , - 2 H 2 H , ( 4G m + 3 K m ) R A²"n , B l - 2 H 1 H , ( 4G m + 3 K m ) h 2n R A²"n ,

A m - H l ( 4 H 3 G M - H 1 H 2 H 5 ) .   B m - H , ( H 1 H 2 H 5 + 3 H 3 K m ) R A -

H 3 - 2 ( H 1 h ² n + H ₂ ) ,    H , - p V H 7 - A ! H 4 H 5 ( 4 n ² - 1 ) - H ₈ ]^{- 1},

H 4 - 4c ³Gm + 3 K m ,    H 5 - h ^{2 n} - 1,    H 6 - c ³ - 1,

H 7 - 16 A 12 H 5 ( A 12 H 4 - 6G m K m H 6 ) ,

H 8 - 8 A 1 1 { A 12 H 4 H 5 + 3 H 6 K m G m [ 2 n ( h ² n + 1 ) - H 5 ] } .

Если предположить, что армирующие элементы однородно распределены внутри композита, то рассматриваемая среда квазиодно-родна и сферически трансверсально-изотропна. Поставим в соответст- вие составным частицам, находящимся в условиях однородного гидростатического растяжения, эквивалентные включения, упругие модули которых являются эффективными деформационными характеристиками композита. Из равенства радиальных перемещений на внешних границах эквивалентных однородных включений ur r - R

pRB

B *^,

3 K Оф и составных частиц

u

M r

I r ^- RB

BM

^- A M R B ⁺   2

R B ²

могут быть найдены оценки сверху для аналогов эффективного модуля объемного сжатия для сферически трансверсально-изотропного дис персно-упрочненного материала со сплошными

K * _- 4G_Mc ³ ( H 1 - 6 K_M ) + 3 K_M ( H , + 8G_M ) *     3 [ H , + 8 G m - c ³ ( H 1 - 6 K m ) ]

и полыми

K

* _- ² H 3 ⁽ A 12 H 4 ^{- 6} H 6 K M G M ^{) -} A 11 H 4 H 9 ^Оф         3 H 1 H 2 H 6 H 5 + 3 H 3 H 10

H9 - H2 (1 - 2n) + h 2nH 1 (1 + 2n),   H10 - 4Gm + 3c3KM включениями. Обратим внимание на то, что замена условий (1) на кинематические (2), обеспечивающие однородное перемещение внешней поверхности составной сферы, позволяет определить константы интегрирования для сплошных

C i - 2 ^ ( 4 G m + 3 K m ) H c R A²~ⁿ ,    A m - 4 H e ( H ₁ + 8G m ) ,

B m - Щ H , - 6 K_M ) H c R A ,   H_c - { R b [ H , + 8G m - ( H , - 6 K m ) c ^; ; '

и полых

A i - - 2 ^ H 2 H , ( 4 G m + 3 K m ) R^ⁿ , B , - - 2I H , H , ( 4 G m + 3 K m ) h 2n R A ^{2+ n} ,

A M - ^ H / [ H 1 H 2 H ₅ - 4 H 3 G M ] , B m - - H I [ H , H 2 H _s + 3 H 3 K m ] R a ,

H 11 ^- A 11 ^{- 4} A 12 ,

H , - { R b [ H 5 H ,, ( 2 H 8 + H 6 H ,, ) - 4 A„n ( H _w + H ,o h 2 n + A ,, H 6 H ₅ n ) _] ' '

включений, а также получить оценки снизу для эффективных модулей к О_ф из равенства радиальных напряжений на внешних границах эквивалентных однородных включений

о

rr

r = RB

3 K

R B

*

Оф

и составных частиц

M            GMB оrr r = Rb 3KMAM 4  „3

Несложно показать, что эти оценки совпадут с полученными выражениями (8) и (9). Следовательно, полученные решения являются точными в рамках ограничений, используемых в полидисперсных моделях. Обратим также внимание на то, что при подстановке R о = 0 в уравнения (9), последние упрощаются и принимают вид (8).

В частном случае E I = E I = 9G I K I /(3 K I + G I ) и б I = о I = ( 3 K I - 2G I )/( 6 K I + 2G I ) из выражений (8) и (9) следуют эффективные модули объемного сжатия двухфазных дисперсно-упрочненных композитов, изотропная матрица которых содержит однородно распределенные изотропные ( n = 1,5) сплошные

K. = 4v,Gm (K, - Km ) + Km (3K, + 4Gm) 3v,(K, - Km)-3K, -4Gm

= Km +(Kl

K )    v, ( G + 3 Km )

M 4Gm + 3K, + 3v, ( Km - K,)

и полые

G , K , ( 1 - h ³ ) ( 4v , G m + 3 K m ) + G M K M ( 1 - v ,*Gi + 3 h ³ K , )

K = 4----- г V-----------7---------------------------- (11)

3 K, [ h3 + 4G, (1 - v, )(1 - h3)] + 4G, ( 4Gm + 3 v,Km )

сферические включения. Обратим внимание на то, что в формулах (10) и (11) проведена замена c ³ = v , (где v , — объемное наполнение), а равенство (10) в точности совпадает с выражением, впервые записанным 3. Хашином [1].

В качестве примера рассмотрим задачу прогнозирования эффективных модулей объемного сжатия полимербетонов - дисперсно-упрочненных композитов на основе полиэфирных смол, армированных диабазовым, мраморным или гранитным щебнем. Матрицы полимербетонов сами являются композитами, наполненными до концентрации Vag < 0,28 молотым известняком, кварцевым песком, мраморной, диа базовой мукой или цементом. Отличительная особенность полимербетонов - высокая (достигающая 0,9) степень наполнения этих материалов минеральными частицами, размер, форма и взаимное расположение которых случайны [4]. Содержание наполнителя в пластмассах изменяется в зависимости от функционального назначения в пределах от 0,1 до 0,4, а объемная доля включений в сферопластиках конструкционного назначения, как правило, не превышает 0,6-0,7.

Большинство исследователей, изучающих полимербетоны, зани маются экспериментальным и теоретическим определением кратковременной и длительной ползучести и долговечности полиэфирных связующих, наполненных минеральной мукой, и материалов на их основе [4-6], а также изучают сорбционные свойства композита [7, 8]. Ограниченное число работ посвящено экспериментальному определению модулей Юнга, коэффициентов Пуассона и модулей объемного сжатия (или их аналогов при неупругом деформировании) в опытах на сжатие и изгиб [4, 7] сухих и влажных (после двухлетней выдержки в воде) образцов. Сравнение спрогнозированных эффективных упругих модулей полимербетонов с использованием аналитических решений, полученных в рамках полидисперсных моделей для композитов с изотропными сферическими включениями, с данными эксперимен тов показывает отсутствие удовлетворительного согласования [5, 6, 9, 10] результатов. Минеральные наполнители имеют ярко выраженную анизотропию свойств, что предопределяет необходимость проверки полученных выражений для эффективных модулей объемного сжатия на их соответствие данным экспериментов.

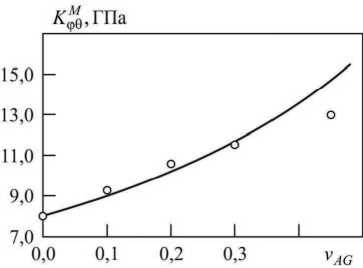
Рис. 1. Зависимость объемных модулей эпоксидной смолы «Диэпокс 450» от объемной доли мраморной муки

На основе полученных аналитических выражений (8) для модуля Kq^ могут быть определены расчетные зависимости этих характеристик для связующих от концентрации частиц минерального наполнителя Vag . Для этого в формуле (8)

необходимо выполнить подстановку c ³ = V ag . На рис. 1 показано изменение эффективного объемного модуля K ( изотропной эпоксидной смолы «Диэпокс 450» ( E = 4,8 ГПа, и = 0,40) при увеличении объемного наполнения мраморной мукой ( E = 55,0 ГПа, и = 0,29, E = 23,0 ГПа и и = 0,32). Сравнение расчетной зависимости с результатами эксперимента [5], которые на рис. 1 показаны точками, свидетельствует о том, что при V ag - 0,3 максимальное отличие значений K ( не превышает 3 %. Существенное несовпадение значений при V ag >  0,3 связано с тем, что при увеличении V a_G в структуре матрицы возникают домены, образованные агрегацией частиц мрамора. Кроме того, при высоких объемных наполнениях уменьшаются минимальные расстояния между включениями, а также при полимеризации эпоксидной смолы возникают поры и межфазные слои, не учитывающиеся в рассматриваемой модели.

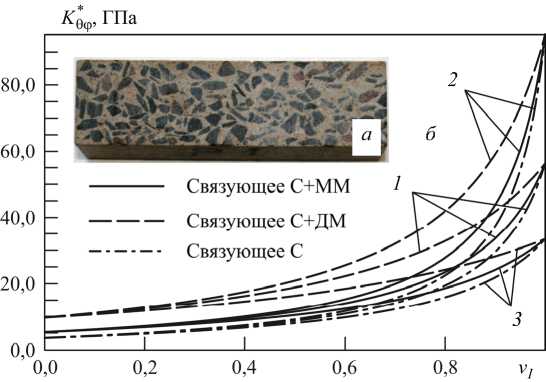
Рис. 2. Случайная структура полимербетона на основе полиэфирной смолы «Диэпокс 450» с базальтовой мукой и гранитными включениями ( а ), эффективные модули объемного сжатия полимербетонов, армированных диабазом (кривые 1 ), мраморными (кривые 2 ) и гранитными (кривые 3 ) сферами ( б )

Количественное совпадение результатов прогнозирования модулей объемного сжатия полиэфирной смолы «Диэпокс 450» позволяет сделать предположение о возможности использования полидисперс- ной модели для описания и оценки влияния типа связующего и минерального наполнителя на эффективные деформационные характеристики полимербетонов. На рис. 2, а представлен образец полимербетона на основе полиэфирной смолы «Диэпокс 450» с базальтовой мукой и гранитными включениями, а на рис. 2, б - эффективные объемные модули Kq^ композитов на основе различных связующих: С (смола «Виналкид 550» без наполнителя), С+ДМ (смола «Виналкид 550» с диабазовой мукой, vAG = 0,28) и С+ММ (смола «Виналкид 550» с мраморной мукой, vag = 0,28), соответствующие следующим упругим постоянным материалов фаз: E = 5,7 ГПа и о = 0,32 (смола С); E = 9,7 ГПа и о = 0,30 (смола С+ММ); E = 11,0 ГПа и о = 0,31 (смола С+ДМ) [9]; E = 88,0 ГПа, и = 0,26, E = 65,0 ГПа и о = 0,23 (диабаз); E = 60,0 ГПа, о = 0,28, E = 40,0 ГПа и о = 0,18 (гранит). Как видим, до объемной доли Vi = 0,73 вне зависимости от типа горной породы, армирующей матрицу, наиболее высокие значения эффективных модулей имеют материалы на основе связующего С+ДМ, а при VI > 0,90 - композиты с мраморными включениями. Полученные зависимости позволяют сделать еще один вывод: для повышения модуля объемного сжатия необходимо отказаться от связующих без минеральных наполнителей, поскольку композит с этим типом матрицы имеет наиболее низкие эффективные характеристики.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ-Урал № 07-01-96056).