Эффективные модули объемного сжатия при плоской деформации двухфазных однонаправленно армированных композитов с анизотропными полыми и сплошными волокнами

Полидисперсные модели механики композитов дают хорошие инженерные оценки для эффективных упругих модулей, если арми-рующими элементами являются бесконечно протяженные цилиндриче-ские соосные круглые в поперечном сечении волокна, размещенные в изотропной матрице [1]. Однако использование этих моделей в случа-ях , если изотропная (эпоксидная или алюминиевая) матрица армирова-на анизотропными углеродными, органическими или природными во-локнами или сама матрица анизотропна (керамическая или поликри-сталлическая), приводит к завышенным значениям эффективных упругих модулей. Поэтому учет анизотропии является одним из спосо-бов «редукции» или более адекватного описания экспериментальных данных для материалов, физико-механические свойства фаз которых не являются изотропными [2].

Еще одним примером материалов, которые могут рассматривать-ся среди возможных приложений, являются биологические костные ткани, состоящие из высокомодульных и высокопрочных неорганиче-ских волокон из кристаллов гидроксилапатита и матрицы в виде орга-нических и коллагеновых волокон (создают монолитность строения). Аморфными органическими и минеральными веществами, которые также присутствуют в костной ткани в объеме 1 %, при прогнозирова-нии эффективных упругих модулей можно пренебречь [3]. Предпола-гая , что волокна из кристаллов гидроксилапатита и коллагеновые во-локна образуют непрерывные нити диаметром до 45 Å, расположенные вдоль продольной оси кости, будем считать, что костная ткань являет-ся трансверсально-изотропной средой. Это предположение не входит в противоречие с выводами авторов [4]. Несмотря на то, что на основе обработки экспериментальных результатов, полученных для образцов из отдельных зон поперечного сечения диафизарного отдела большой берцовой кости, делается вывод об ортогональной анизотропии мате-риала, различие в модулях нормальной упругости в окружном и ради-альном направлениях не превосходит 7,5‒8,0 %.

Принимая гипотезы полидисперсных моделей [1], рассмотрим двухфазный композит, линейно- -изотропная матрица которого армирована сплошными или полыми со-осными трансверсально-изотропными круглыми в поперечном сечении волокнами различного диаметра. Будем считать, что каждое цилинд-рическое волокно произвольного радиуса RA , окруженное слоем мат- рицы толщиной RB- RA, является составным армирующим элементом, для которого отношения c RA/RB и h R0/RA (в случае полого армирующего элемента) являются постоянными величинами. Кроме того , будем предполагать, что волокна, матрица и составной армирующий элемент не изменяют тип упругой симметрии при нагружении, имеют ось симметрии бесконечного порядка, совпадающую с осью z цилиндрической ортогональной системы координат r, 9 и z.

Рассмотрим произвольный бесконечно протяженный составной армирующий элемент, находящийся в плоскодеформированном состоянии , на внешней боковой цилиндрической поверхности которого задано равномерно распределенное радиальное давление p :

°Л r₌RB = Р                          ⁽1)

или перемещение :

“r l R (2)

Используя точные аналитические решения задач Ламе о равнове-сии толстостенных трансверсально-изотропных цилиндров [5], запишем выражения для радиальных перемещений “г и напряжений Г5_гг в полом волокне и окружающем слое матрицы:

“r=A^r + — , OI. A22 f AF   F) + A23 f af + ~F) , r V      r 2V r )

M     BM  M        BMB

“r AAMr^ , rrrr- 2222 AM        B23 AM + ~ • r V      r2) V r )

Здесь и далее все величины, относящиеся к волокнам и матрице, будут отмечены индексами F и M соответственно.

Для композита со сплошными волокнами в уравнениях (3) исключим слагаемые, содержащие B I . Наличие этих слагаемых в решении приведет к сингулярности радиальных перемещений и напряже-ний в точках, принадлежащих оси симметрии армирующих элементов:

“r ⁼ Fp^r , rrrr ⁼ CF^A 22 ⁺ A 23) .                    ⁽⁵⁾

Содержащиеся в равенствах (3)‒(5) константы определяются мо-дулями Юнга E_M , E_M , E_F , E_F и коэффициентами Пуассона и M , б M , и F и б F :

A ₂₂

EF

HF (1+ и F Л

1- б ^{2 E F} , A       ^{E F}

^F E_F , A 23 _HF (1+ V F)

E

V F + б 2 _F F , E_F

B 22

EM     1 2 E_{M  B}      E_M ---f + г2 EM

^M , B ₂₃   И (А _M^M

HM (1  Mл    EM      HM (1Mл

HF 1-и F 2б ² _{F E} ^F , H_M 1-и M 2б 2 _M EM _.

EFE

Ограничимся наиболее простым случаем, когда на межфазной поверхности композита выполняются условия идеального сопряжения urI I       = urM I ,о rIr I - = о rMr I,

r r RA r r RA    rr r RA     rr r RA а внутренняя поверхность полых цилиндрических включений свободна от напряжений,

rr I r R ₀ 0 .

Из решения системы линейных алгебраических уравнений, кото -рая получается при подстановке (4) и (5) в равенства (1) и условия (6), :

B ₂₂          K ₁ + K 4          2 K 3 - K ₁

F 2 H p , AM    H   p , BM RAp

HC        HCH

K  EF K   EF  K  EM K

K1       , K 2         , K3       , K 4,

HF      1 + и F      HM      1 + V M ,

HC K 4 ( K 1 K 3 ) c ² + K 3 ( K 1 + K 4 )

для композита, армированного сплошными цилиндрическими волок-нами . В случае когда волокна полые, записать систему алгебраических уравнений и решить ее относительно неизвестных постоянных

A_F   2 ^{K 2 B 22} p , B       K ₁ B ₂₂ R ₀ ²

A_F   2 p , B_F   2 p ,

HH

_A    K 1 ( K 2 K 4 ) h ² K 2 ( K 1 ± K 4 )

p ,

AM

H

B    ^{K 2}( K 1 K 3 ) RA ² K 1 ( K 2 + K 3 ) R 0²

p ,

BM

H

H K 4 c ² K 1 ( K 2 + K 3 ) h ² K 2 ( K 1 K 3)]+ + K 3 K 1 ( K 2 K 4 ) h ² K 2 ( K 1 + K 4 )]

позволяет подстановка (3) и (4) в соотношения (1), условия (6) и (7).

Если предположить, что волокна однородно распределены внут-ри композита, то рассматриваемая среда квазиоднородна и трансвер-сально-изотропна. Поставим в соответствие составным частицам, на-ходящимся в условиях плоской деформации, эквивалентные однород-ные армирующие элементы, упругие модули которых являются эффективными характеристиками композита.

Из равенства радиальных перемещений на внешних границах эк-Бивалентных однородных армирующих элементов uI _ = pRB ur r RB       *

2 K_r 9

и составных волокон uM I п =AR = + BM ur r RB AMRB

RB могут быть найдены оценки сверху эффективных модулей объемного сжатия при плоской деформации двухфазного композита со сплошными

_K * _r    1 K 4 ( K 1 K 3 ) c ² + K 3 ( K 1 + K 4 )

r 2     ( K ₃ K ₁ ) c ² + K ₁ + K ₄

и полыми

_K * 1 K 4 K 1 c ² + K 3 K 2 K_r

2 K ₂- K ₁ c ²

соосными волокнами, находящимися в идеальном сопряжении с транс-версально-изотропной матрицей.

Здесь K ₁ K ₂ ( K ₁ K ₃)- K ₁ ( K ₂ + K ₃ ) h ² , K 2 K ₂ ( K ₁ + K ₄)- K ₁ ( K ₂ K ₄ ) h ² .

Обратим внимание на то, что замена условий (1) на кинематиче-ские (2), обеспечивающие однородное перемещение внешней боковой поверхности составного цилиндрического волокна, позволяет опреде-лить константы интегрирования для сплошных

Г -2

F 2

B ₂₂ A ^{K 1} 1 K 4 B cR Z K ₁

RH , _M RH , _M c R_B

RBHC       RBHC            HC

HC = ( K 3 K 1 ) c ² + ( K 1 + K 4 )

и полых

A 2 ^{2 22} .         K ₁ B ₂₂ R _B h ² c ²

AF ² R ² BH ²  , B_F 2 ^{1 22} _H ^B

AM

K 1 ( K 4 K 2 ) h ² + K 2 I K 1 + K 4 )

RBH

B_M c ² R_B

K 1 ( K 2 + K 3 ) h ² K 2 ( K 1 K 3 )

H

H A ₂₂ A ₂₂ h ² - 1 c ² 1    h ² + 1 c ² K ₃ + K ₄ )] ⁺

+ A ₂₃ h ²  1 c ² K ₃ + K ₄ + A ₂₃ 1 c ²

армирующих элементов, а также получить оценки снизу для эффек-

K_r ^*

внешних боковых границах эквивалентных однородных волокон

° rr | r RB

2 K RB

*

r 9

и составных армирующих элементах

ГТ ^M I ₌AK   B M K 4

.

rr r R_B  A_MK _{3     2}

RB

Несложно показать, что эти оценки совпадут с полученными вы-ражениями (8) и (9). Следовательно, полученные решения являются точными в рамках ограничений, используемых в полидисперсных мо-делях. Обратим также внимание на то, что при подстановке R0 0 (или h 0) в уравнения (9) последние значительно упрощаются и при-нимают вид (8).

В частном случае

E_F E_F 9 ^{G F K F} , E_M E_{M 9} G_MK_M 3 K_F + G_F ^{, M M}   3 K_M + G_M

,

• -       3 K_F - 2 G_F -         3 KM - 2 G

• V _F — V _F            ^,V _M — V _M             ,

6KF + 2GF          6KM + 2GM где KF , KM , GF и GM — объемный и сдвиговой упругие модули фаз, из выражений (8) и (9) следуют эффективные модули объемного ежа-тия при плоской деформации волокнистых композитов, изотропная матрица которых содержит однородно распределенные изотропные сплошные

K*r 3GMI NM NF >F "(NF + 3GM ) NM r 3 NF NM F 3 NF 3GM

KM + ¹ ₃ GM + ---------- ---- F 1

311 _F

KF + 13 GF KM + 13 GM KM + 43 GM и полые

K ^* r 3 GFGM I N_F N_M > F GMNF ( 3 G_F + N _M ) v ₀ V F +^{NM N K} , (11) N_F ( 3 G_F + N_M ) v ₀ V F + 3 G_F ( N_M N_F )v F + 3 N_K    ^,

NK =(GM GF ) NF V0+ GF ( NF + 3GM ), NM GM + 3KM , NF GF + 3KF цилиндрические соосные армирующие элементы. Обратим внимание на то, что в формулах (10) и (11) проведена замена c2 vF и h2 v0 (где vF и v0 ‒ объемное наполнение волокнами и пористость), а равен-ство (10) в точности совпадает с выражением, впервые полученным 3. Хашином и Б .В. Розеном [1].

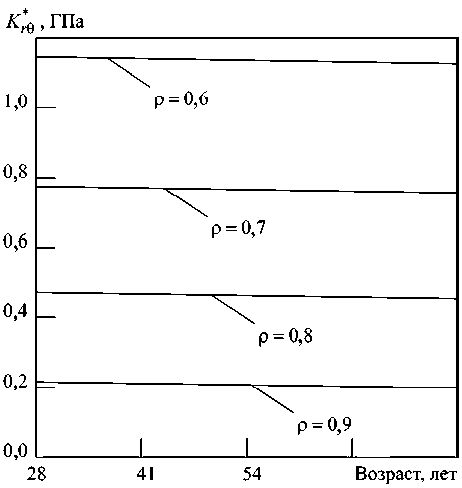
Рис . Возрастные изменения модуля объемного сжатия при плоской деформации трабекулярной костной ткани при различной объемной пористости р = R 0 / R B

В качестве примера рассмотрим задачу прогнозирования возрас-тного изменения эффективных модулей объемного сжатия при плоской деформации трабекулярной ткани большой берцовой кости. Для этого предположим, что костная ткань является композитом с круглыми в поперечном сечении соосными туннельными порами. Моделирова-ние возрастного изменения деформационных характеристик будем проводить с использованием эмпирической зависимости [6], получен-ной в результате обработки экспериментальных значений модулей нормальной упругости в различных возрастных группах от 28 до 95 лет . Считая, что возрастные изменения влияют только на модули в про-дольном направлении, примем следующие упругие характеристики ко-стной ткани: E 7,7 ГПа,и =0,44, E 21,7 ГПа и б = 0,3 (возраст ‒ 28 лет)и E 7,7 ГПа ,и =0,44, E 17 , 4 ГПа и б = 0,3 (результат био-логического старения до 80 лет) [4, 6].

С помощью полученных выражений (9) будем прогнозировать

Kr* трабекулярной костной ткани. Эта характеристика является одной из ключевых для описания движения вязких жидкостей (костный мозг, лимфа, кровь, тканевая жидкость) внутри [7]. Примем следующую ги-потезу : 28 лет ткань является «молодой», а при увеличении биологического возраста старение начинается на внутренних поверх-ностях и постепенно к 80 годам охватывает весь объем кости. Это предположение позволяет заменить исходную стареющую среду ком-позитом с полыми соосными цилиндрически трансверсально-изотроп-ными волокнами в трансверсально-изотропной матрице (стареющая и«молодая» костная ткань соответственно), с равномерно изменяющи-мися радиусами: h R0 /Rл =1 в возрасте 28 лет до c RA / RB 1 ‒ 80 лет.

Еще один важный фактор, который может быть учтен при про-гнозировании эффективных упругих модулей — необратимые измене-ния в структуре костной ткани при наличии, отсутствии или изменении внешнего силового воздействия . Закономерности этих изменений, свя-занных с разрушением «старых» и созданием новых трабекул, подчи-няются закону Ю . Вольфа [8]. Будем предполагать, что перестройка костной ткани связана с увеличением объемной пористости р = R ₀ / R_B , которая будет изменяться в диапазоне от 0,6 до 0,9.

На рисунке показано совместное влияние объемной пористости и биологического возраста на изменение модуля объемного сжатия при плоской деформации трабекулярной костной ткани. Как видим, при ста-

( 2 8 %) K_r ^* , -мя как при увеличении объемной пористости до 0,9 значения эффектив-ных модулей в 5,2‒5,7 раз ниже, чем в исходном состоянии (Р = 0,6).

Обратим внимание на практическую значимость полученных ре-зультатов . Спрогнозированное изменение модулей объемного сжатия при плоской деформации связано с возрастной внутренней перестрой-кой структуры костной ткани и является основой для разработки но-вых методов предупреждения и лечения переломов, а также обоснова-ния комплекса гимнастических упражнений и индивидуального подбо-ра нагрузок для неподвижных и ограниченно подвижных больных.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ № 11‒01‒00910).