Эффективные наборы совместно вычисляемых линейных локальных признаков цифровых сигналов

Построение признаков и алгоритмов их вычисления – один из ключевых этапов разработки большинства систем, связанных с обработкой и анализом цифровых сигналов и изображений. При реализации этого этапа в конкретной системе требуется удовлетворить многим требованиям, которые не только противоречивы, но и не всегда допускают чёткую математическую постановку [1-3]. Учитывая также многообразие практических постановок задач обработки и анализа, следует признать проблему построения признаков чрезвычайно сложной. Дополнительным подтверждением этому является отсутствие в настоящее время развитой конструктивной теории построения признаков сигналов и изображений для решения задач обработки и анализа. Как следствие, качество принимаемого решения – выбранной системы признаков и алгоритмов их вычисления – целиком и полностью зависит от человека, разрабатывающего конкретную прикладную систему обработки и анализа сигналов и изображений, от его квалификации, опыта, кругозора и затраченных усилий.

Настоящая работа, продолжающая цикл работ [46] автора, направлена на формализацию и решение проблемы построения признаков и алгоритмов их вычисления для вполне определённого класса задач обработки и анализа цифровых сигналов и изображений. Ограничение класса задач определяется моделью используемых признаков - допускается, что для решения задачи обработки и анализа достаточным является использование линейных локальных признаков . Значение ЛЛП вычисляется как линейная свёртка значений отсчётов сигнала/изображения, попавших в область анализа, с некоторым наперёд заданным набором «весов», которые в совокупности составляют

КИХ. Способ выбора набора весов в КИХ характеризует способ построения ЛЛП, а способ вычисления линейной свёртки – алгоритм вычисления признака. Учитывая, что многие известные признаки (коэффициенты разложения Фурье в окне, коэффициенты вейвлет-разложения, локальные степенные и полиномиальные моменты и т.п.) [1,2,8] соответствуют выбранной модели, принятое ограничение не представляется чрезмерно жёстким.

Естественным, но обычно плохо формализуемым требованием к признакам является их «эффективность» [1,4]. В рамках предложенного в работах [5,6] автора подхода под «эффективностью» признака понимается удовлетворение двум требованиям:

• •    алгоритм вычисления признака должен обладать заранее заданной (и минимальной в некотором класса) вычислительной сложностью;

• •    КИХ признака должна быть наилуч шим образом согласована с наперёд заданным критерием качества.

При выполнении указанных требований эффективные ЛЛП позволяют установить рациональный баланс между двумя противоположными группами признаков:

• •    признаками, оптимальными в смысле некоторого критерия качества, но не имеющими подходящего или быстрого алгоритма вычисления (например, признаки, полученные с использованием преобразования Карунена-Лоэва);

• •    признаками, полученными с использованием быстрых алгоритмов, но не имеющими отношения к содержательной постановке задачи и соответствую щим критериям качества (например, признаки, полученные с использованием алгоритма быстрого преобразования Фурье).

В работах [5,6] автора предложен подход к построению отдельных эффективных ЛЛП. Настоящая работа развивает указанный подход на случай построения эффективных наборов совместно вычисляемых ЛЛП. В отличие от предложенных в работах [5,6] признаков, набор совместно вычисляемых ЛЛП имеет один алгоритм, который производит одновременное/совместное вычисление сразу нескольких линейных свёрток одного входного сигнала/изобра-жения с набором различных КИХ.

1. Набор линейных локальных признаков и алгоритм их вычисления

Пусть R, R + , Z, Z + , N - множества, соответственно, вещественных, вещественных неотрицательных, целых, целых неотрицательных и натуральных чисел; K - коммутативное кольцо с единицей, F -коммутативное поле.

Определение 1. Набором из R совместно вычисляемых ЛЛП длины M над K называется пара

I { hr ( m ) } m =0 M 1, , A I , где { hr ( m ) } m =0 M 1, ^- набор ^             r =0, R -1        )                        r =0, R -1

из R КИХ-ик, каждая из которых задаётся в виде конечной последовательности над K и удовлетворяет ограничениям hо (0) * 0,

V r e 0, R - 1 3 m e 0, M - 1 h_r ( m ) * 0,        (1)

3 r e 0, R-1 hr (M -1)* 0;

а A - алгоритм вычисления набора линейных свёрток произвольного входного сигнала { x ( n ) } N 1 над K с набором КИХ { h r ( ^m ) } m =0 M 1, ( ^M <  N ) ^:

r =0, R -1

M -1

Уг ( n) = hr ( n ) * x ( n ) = S hr ( m ) x ( n - m) ’ m=0                            (2)

n = M - 1, N - 1, r = 0, R - 1.

Для сокращения изложения вместо понятия «набор совместно вычисляемых ЛЛП» далее в тексте будем использовать словосочетание «набор ЛЛП».

Следующие два определения являются обобщениями определений известных понятий линейной рекуррентной последовательности (ЛРП), линейного рекуррентного соотношения (ЛРС) [9-11] и понятия расширенного ЛРС (РЛРС), введённого и использованного в работах [5,6].

Определение 2. Пусть K,T, R e N (R > T), а a^kU{«^

- заданные элементы

r =0, R -1

r =0, R -1

из K . Набор из R последовательностей h0 (0),h (1),...;hR-1 (0),hR_,(1),... над K , удов- летворяющих соотно шению bm,  r = 0, T-1, m = 0, K -1, hr (m) = •

min ( K , m )

S a0khr ( m - k ) + k=1

min ( r , T -1 ) min ( K , m )

+ S S atkhr -1 ( m - k )+Ф r (mX t =1          k = 0

r > T v m > K, называется

набором линейных   взаимно- рекуррентных последовательностей (ЛВРП)

( T, K)-го порядка над K . Первые члены

{ b_rk } _r = 0 T 3, однозначно определяют набор ЛВРП k =0, K -1

и называются его начальными значениями . Выражение (3) называется линейным взаимнорекуррентным соотношением (ЛВРС) ( T, K)-го порядка, а коэффициенты a"_k - коэффициентами

ЛВРС . Если все последовательности конечны и определены на области m = 0, M - 1 ( K <  M ) , то пару ( R, M ) назовём параметрами области определения набора ЛВРП. Величины ф _r ( m ) -свободные члены ЛВРП. При этом, если на всей области определения ЛВРП ф _r ( m ) = 0, то соответствую щее ЛВРС называется однородным , в противном случае – неоднородным .

По аналогии с коэффициентами ЛРС всё упоря- доченное множество

{^tVГк U{ arV K

r =0, R -1

r =0, R -1

эффициентов ЛВРС целиком обозначим в виде век- тора a .

Для конечных ЛВРП за пределами области определения положим

hr (m ) = 0 m 6 0, M - 1v r 6 0, R -1

и рассмотрим последовательности:

ф r (m) = hr (m )-

Г^

Z a 0k h r ⁽ m ^{- k ) +}

• - k =1

min( T-1, r) K,

• + Z   Z a rk h r - 1 ( m - k )

4           t =1       k= 0

m e Z , r = 0, R - 1.

Определение 3. Пусть { h r ( m ) } _m =0 M - , - набор r =0,’ R -1 ’

ЛВРП порядка ( T , K ) над K с параметрами области определения ( R , M ) . Представление набора ЛВРП в виде:

0,                       m <  0,

K

Z a"йЛ ( ^{m - k} ) ⁺

k =1

h r ( m ) = <

min ( T -1, r )

+ Z t=1

K

Zakhr -1 ( m-k )+Ф r (m)’ k=0

r = 0, R -1, m = 0, M + K -1, где отсчёты фr (m) задаются соотношениями (4), называется расширенным ЛВРС (РЛВРС) порядка (T, K), а вектор (R, M, T, K, a) - вектором параметров РЛВРС.

В дополнение к данному определению введём следую щие множества:

r , m ) : r = 0, R - 1, m = 0, M + K - 1 } ,

] ⁰ [ =

(r, m): фr (m) ^ 0, r = 0, R -, m = 0, M + K-1

И определим множество 0 следующим образом ( =' = = ) :

• 0 = ]0[ U s'.

Введённое множество 0 (включающее множество ] 0 [ как подмножество) назовём множеством отсчётов неоднородности РЛВРС, отсчёты множества 0 - отсчётами неоднородности РЛВРС, величины ф _r ( m ) - значениями неоднородности в соответствую щем отсчёте. Очевидно, что во множество ] 0 [ попадают только те отсчёты неоднородности, которые содержат ненулевые значения и в которых действительно нарушается однородность РЛВРС.

Заметим, что для набора КИХ, для которых справедливо ограничение (1), множество 0 отсчётов неоднородности РЛВРС удо влетворяет условию:

( 0,0 ) e0 ,     3 r e 0, R - 1: ( r , M + K - 1 ) e0 . (6)

Для удобства определим также подмножества множества 0 отсчётов неоднородности РЛВРС, задав их для каждой последовательности в наборе:

0r ={(5,m)e 0: 5 = r}, r = 0,R-1.

Очевидно, справедливы следую щие соотно ше-ния:

Vr ^ 5 0r n 05 = 0;    0 = U 0r.

r =0

R -1

]0[E0, ]0 r [E0 r , ]0[ = U ]0 r [ .

r =0

Тогда вычисление свёрток (2) входного сигнала с набором из R ЛВРП порядка ( T , K ) над K с параметрами области определения ( R , M ) и множеством отсчётов неоднородности 0 может быть выполнено с использованием следующего алгоритма.

Алгоритм A ³

Вход : { x ( n ) } n - _- ; Выход : { y_r ( n ) } _n = M r^ .

,                                     r =0, К -1

• 1)    Предварительная обработка:

yr (n )= Z x (n - m )ф r (m), me0r                                             (7)

n = 0, N - 1, r = 0, R - 1.

• 2)    Окончательная обработка:

Уг (n) = Za«Уг (n - k) + k=1

min ( T -1, r ) k

+ Z   Z a*yr-1 (n - k)+ yr (n) ,           (8)

• t =1       k =0

n = 0, N - 1, r = 0, R - 1.

В представленном алгоритме приняты следующие согла шения:

• -    значения отсчётов x ( n ) для случая n <  0 полагаются равными нулю;

• -    значения отсчётов y_r ( n ) для случая n <  0 или r <  0 полагаются равными нулю.

Вычислительную сложность этого алгоритма, по аналогии с работами [1,4,5,6, 8,12], будем оценивать числом арифметических операций сложения и умножения, необходимых для получения результата, а именно: пусть U add ( A ³ ) и U mul ( A ³ ) - число арифметических операций, соответственно, сложения и умножения, требуемых для получения всех выходных отсчётов сигнала в алгоритме A ³ . Общую вычислительную сложность алгоритма A ³ определим в виде:

U ( A 3М addUadd ( A 3Н muUmul ( A3) , где 5add + 5mul = 1, (^add , Smul e R + ) • Для анализа вы числительной сложности алгоритма далее будем использовать приведённую вычислительную сложность, задаваемую в виде:

u ( A ³ ) =

N - M + 1

U ( A ³ )

Определение 4. Набор ЛВРП { h r ( m ) } _r = o r - . над m =0,1,..

K, представимых в виде РЛВРС с вектором параметров ( R , M , T , K , a ) и множеством отсчётов неоднородности 0 , называется набором взаимнорекуррентных МС-последовательностей ¹ с аналогичным вектором параметров, если последовательности набора удовлетворяют ограничениям (1) и для множества 0 отсчётов неоднородности РЛВРС выполняется условие:

|] 0 [| <  1 + RK .

Для случая одной последовательности (R=1) по- следнее определение также приводит ко введённому в работах [5,6,12] ограничению в виде: |]0[| < 1 + K •

Введём дополнительно следующие множества:

{ ( r , m ) :

r = 0, R - 1, m = 0, M - 1 } ,

Приведённая вычислительная сложность, как очевидно, равна среднему числу арифметических операций, требуемых алгоритмом A ³ для получения одного «выходного» набора значений свёрток в (1). В случае набора, состоящего из одной КИХ, приведённая вычислительная сложность равна среднему числу операций, требуемых для получения одного выходного значения.

Прямым подсчётом числа арифметических операций в алгоритме A ³ можно убедиться в справедливости следую щего предложения.

Предложение 1. Вычислительная сложность алгоритма A ³ для ЛВРП порядка ( T, K ) с параметрами области определения ( R , M ) и множеством отсчётов неоднородности 0 имеет вид:

0* ={( r, m)e 0 : m = M + K -1}.

Определение 5. Набор взаимно-рекуррентных МС-последовательностей над K с вектором параметров ( R , M , T , K , a ) называется нормализованным, или НМС-набором последовательностей типа ( b , c , d ) ( b , c e K \ { 0 } , d e K ) для множества отсчётов неоднородности 0 , если для значений неоднородности { ф Г ( m ) }       и

( r , m ) e0

последовательностей { h r ( m ) } _{r =} 0 R - набора вы- m =0, M -1

полняются условия: h ₀ ^* ( 0 ) = b и

u(A3) =

N

| 0- R 5 add +

= arg max

¹ {ф ( m )l        ,

I ^{{V r ( )}} ( r , m ) e0

I { h r ( ^m ) } r = 0: R — 1

V          m = 0, M - 1 ,

-------------- .       . ( Т — А

N-M + 1 +(K + 1)TI R-T—1Iх I 2

- R7

В приведённом выражении | • | - мощность соответствую ще го множества, в данном случае – число отсчётов неоднородности. Заметим, что выражение (9) не учитывает возможные тривиальные значения множителей и слагаемых в (7)-(8), давая выражение в общем виде.

Для случая одной КИХ, когда R = T=1 , выражение (9) принимает вид

I ( R ² ( M + K ) + 1 )    ^    I ( ф , ( m ) = 0 ) +

( ^r • m )^e0 \ ^{( ⁰-⁰ ) }

^{+ R} ( ^{M + K} ) ^ ¹ ( ^ф r ( ^m ) = c ) ⁺

( r , m ) e0 *

+ E   1 (hr (m )=d)+

( r , m )ea \ { ( 0,0 ) }

.

⁺ 2exp

—

^ 8 r ( M + K ) + m ( r , m ) e0

u (A 3)= м Z 1 (I0 + K-^)N - M + и в точности совпадает с приведённым в работах [5,6] выражением для вычислительной сложности алгоритма расчёта отдельного ЛЛП.

V

к

V

+ E 8 r ( M ^{+ K ) +} m V ( r , m )e.=.

⁴ 1 (< f r ( ^m ) = ⁰ ) ^{+ 3} + 2 1 ( ф _r ( m ) = c ) ^

I ( h r ( m ) = d )

В приведённом выражении величина I ( • ) - индикатор соответствую щего события/условия, кото-

• 2.    НМС-набор последовательностей Введём ограничения на возможные ЛВРП.

¹ Аббревиатура MC введена в работе [8] и расшифровывается как Minimal Complexity (минимальной сложности).

рый принимает значение «1», если условие выполняется, и «0» - в противоположном случае.

Определение 5 и условие (11) требуют некоторых комментариев. Для заданного множества отсчётов неоднородности 0 могут быть построены различные наборы взаимно-рекуррентных МС-последовательностей с указанным вектором параметров (R, M, T, K, a), но различными итоговыми множествами ]0[ и ]ф (тИ и отсчётами по-J L I r ( ^CГ,т)e]0[ следовательностей в наборе. Среди всех этих наборов выбирается такой, который даёт максимум показателя в (11). Значение показателя формируется че- тырьмя слагаемыми, в каждом из которых есть «весовая» составляющая и «индикатор». Из соотноше- ния «весовых» составляющих следует, что величина

У I(фr (т) = 0) (r, т )e0 \{( 0,0)} должна быть увеличена в

первую очередь, второй следует увеличивать вели- чину У I (<фr (т ) = c), третьей - величину (r, т )e0

У   I ( hr ( т ) = d )

(r, т )e = \{( 0,0)} и, наконец, последним сле-

дует увеличивать последнее слагаемое (значение экспоненты, которое по абсолютной величине не превосходит «0,5»). Проанализируем теперь каждую из этих величин.

Для «индикатора» в первом слагаемом справедливо соотношение:

У I ( ^ф r ( т ) = ° ) = |©|-Н .

( r , т ) e0 \ { ( 0,0 ) }

Поэтому рост величины в левой части приводит к уменьшению величины |]0[| . Это эквивалентно построению набора последовательностей с минимально возможной мощностью множества ] 0 [ , то есть с минимальным количеством нарушений однородности у РЛВРС. Рост «индикатора» второго слагаемого приводит к росту значений отсчётов неоднородности из множества 0 с величиной « c ». Рост последнего, третьего слагаемого приводит к росту числа отсчётов в наборе последовательностей со значениями « d ».

Для увеличения показателя в (11) рост первых трёх слагаемых происходит именно в этой (указанной) последовательности. При этом если максимум суммы первых трёх слагаемых достигается всего для одного набора последовательностей, то значение четвёртого слагаемого (экспоненты) не влияет на выбор набора последовательностей (оператор максимума), поскольку дополнительная коррекция этого слагаемого не превосходит «0,5». С другой стороны, если максимум суммы первых трёх слагаемых достигается на нескольких наборах, то последнее (экспоненциальное) слагаемое вводит строгое упорядочивание решений путём идентификации с каждым из них последовательности длины R(M+K), каждый элемент которой имеет значения из множества {0,..., 7} . Вводимое упорядочивание - лексикографическое, порождаемое выражением:

у ₈ r ⁽ M ₊ K ^{)+ т} ( 4 1 ( ф r ( т ) = 0 ) + 2 1 ( ф _r ( т ) = c ) ) +

( r , т ) e0

+ у 8 ^{r (} M ^{+ K )+ т} 1 ( h r ( т ) = d ) .

( r , т И

Справедлива следую щая лемма.

Лемма 1. Для НМС-набора последовательностей типа ( b , c , d ) ( b , c e K \ { 0 } , d e K ) с вектором параметров ( R , M , T , K , a ) вычислительная сложность алгоритма A ³ вычисления соответствующих ЛЛП удовлетворяет условию:

u ( A ³ ) <

N

N - M + 1

^{R ( K} — ^{1 )-( R} — O^ add ⁺

+ ( ^K + ¹ ) ^{T f R} — ^ 1

V              V 2 ) )

Доказательство :

Соотношение (12) напрямую следует из выражения (9) и условий определений 4-5.

□

В частном случае, когда R = T =1, соотношение (12) преобразуется к виду:

u(A3)<---N---2K , v ' N - M + 1

что в точности совпадает с приведённым в работах [5,6] соотношением для вычислительной сложности расчёта ЛЛП для отдельной    НМС- последовательности.

Другим важным частным случаем, который будет рассматриваться и далее, является НМС-набор последовательностей порядка ( T , K ) = ( 2,1 ) . Выражение (12) для вычислительной сложности алгоритма A ³ расчёта набора ЛЛП преобразуется к виду:

u ( A ³³ ) < ^У1 ( R ( ³ + ⁵ " | ) - ^{2 + 5} ‘ - ) .    ⁽¹³⁾

N - M + 1

• 3.    Существование и единственность НМС-набора последовательностей.

Построение НМС-набора последовательностей

В настоящем и следую щи х двух разделах предполагается, что отсчёты набора последовательностей (набора КИХ) и компоненты вектора коэффициентов РЛВРС а являются элементами некоторого коммутативного поля F .

Теорема 1 (о существовании и единственности НМС-набора последовательностей).

Пусть ( R , M , T , K , a ) - вектор параметров РЛВРС и множество 0 отсчётов неоднородности удовлетворяет соотношению (6) и ограничению:

10| = 1 + RK ,                                   (14)

НМС-набор     последовательностей типа

( b , c , d ) ( b , c e F \ { 0 } , d e F ) над F с вектором параметров ( R , M , T , K , a ) для множества отсчётов неоднородности 0 либо не существует, либо существует и единственен.

Доказательство:

В соответствии с определением РЛВРС набор взаимно-рекуррентных МС-последовательностей должен удовлетворять (5) на всей области определения. Записывая по одному уравнению для каждого отсчета из множества Е

Е= { ( r , m ) : r = 0, R - 1, m = 0, M + K - 1 } , |E| = R ( M + K ) кроме (0,0), а также учитывая ограничение h о ( 0 ) = b ( = ^ф о ( ° ) ) для НМС-набора последовательностей, получим следующую систему линейных алгебраических уравнений (СЛАУ) c R ( M+K) уравнениями:

h ° ( ° ) = 1,         r = °, R - 1:

h r ( m ) - L> r h ( m — k ) — k =1

min ( T -1, r ) K

• ^-    L  L ah - 1 ( ^{m - k} ) = °,

t =1       k =0

{ 1, ^ , M - 1 } \ 0 0 , r = 0, { 0,-.., M - 1 } \ 0 _r , r >  0,

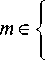
K                        min ( T -1, r ) к

L a 0k h r ( ^{m - k} )⁺ L   L ah - 1 ( ^{m - k} ) = ⁰

k =1                               t =1        k =0

m e{ M,..., M + K-1} \ 0 r, hr (m)- La 0khr (m - k)-k=1

min ( T -1, r ) K

• -    L   Lah-1 (m-k)-фr(m)=0,

t =1       k =0

m e { 0,..., M - 1 } П 0 _r ,

L a 0 rk h r ( m ^{- k} ) ⁺ k =1 min ( T -1, r ) K

• ⁺    L   L ah - 1 ( ^{m - k} )^+ф r ⁽ m ) = ⁰      (15)

t =1       k =0

m e { M ,..., M + K - 2 } П 0 _r .

В этой СЛАУ переменными являются значения искомых последовательностей { h_r ( m ) } _m =0 M - , (ко- r =0,’ R -1 ’ личество значений - RM ) и значения неоднородности { ^Ф r ⁽ m ) } ₍ r , m \ { ^Ф 0 ^{( 0 )} } (| ⁰ \ ^{{( 0},^{0 )}}| = RK ) . Таким образом, в приведённой СЛАУ всего R ( M+K)

переменных. Она может быть совместна или несовместна.

Если ранги расширенной и главной матриц СЛАУ не совпадают, то СЛАУ (15) оказывается несовместной. Следовательно, искомый НМС-набор последовательностей не существует.

Если ранги расширенной и главной матриц СЛАУ совпадают, то СЛАУ совместна. Тогда возможны две различные ситуации.

В первой ситуации равные ранги главной и расширенной матриц СЛАУ имеют значение R ( M+K). Тогда решение СЛАУ существует и единственно [13]. В этой ситуации возможны два случая.

• -    Условие (1) для решения СЛАУ выполняется .

Тогда ре шением СЛАУ является НМС-набор последовательностей с заданным вектором параметров ( R , M , T , K , а ) и множеством отсчётов неоднородности ] 0 [ с 0 (множества могут не совпадать, поскольку некоторые из значений неоднородности могут оказаться нулевыми). В силу единственности решения СЛАУ условие (11) выполняется автоматически и НМС-набор последовательностей единственен.

• -    Условие (1) для решения СЛАУ не выполняется. Тогда получаемый в результате решения СЛАУ набор последовательностей не удовлетворяет условию определения 4 и, как следствие, не является НМС-набором последовательностей. То есть искомый НМС-набор последовательностей не существует.

Во второй ситуации равные ранги главной и расширенной матриц СЛАУ имеют значение меньшее R ( M+K) (но не меньше единицы в силу равенства h ₀ ( 0 ) = 1) . Следовательно, существует множество решений СЛАУ (15). Причиной этому является то, что число (линейно-независимых) уравнений оказалось меньше, чем число переменных. Выходом из этой ситуации является пополнение СЛАУ (15) некоторым количеством дополнительных уравнений. Первой группой таких уравнений являются следующие RK уравнений-равенств, которые «продуцируются» первым слагаемым в критерии (11):

фr (m) = 0, (r,m)e0\{(0,0)} .(16)

Вторая группа из 10* | (1 -10*| - R) уравнений- равенств «продуцируется» вторым слагаемым в (11): фr (m ) = c, (r, m )e0*.(17)

Третья группа содержит RM - 1 уравнений-равенств и «продуцируется» третьим слагаемым в (11):

hr (m) = d, (r,m)eE\{(0,0)} .(18)

Общее количество дополнительных уравнений, задающи х посредством операции присвоения значения неизвестных, удовлет воряет соотношению:

RK + |0’| + ( RM - 1 ) =

= R (M + K ) + |0*| -1 > R (M + K), что достаточно для пополнения СЛАУ до Краме-ровской. Причём если в СЛАУ использовать сразу все уравнения (16)-(18), то СЛАУ оказывается переопределённой и неразрешимой. Следовательно, разрешимая непротиворечивая СЛАУ находится среди r ( m + k )+|э*|-1

всех возможных 2        пополненных СЛАУ.

Как и для первоначальной СЛАУ, каждая из этих

^R ( M + K ) +Ы-1

• 2         пополненных СЛАУ может быть несо

вместной или совместной. Совместные СЛАУ могут быть Крамеровскими (однозначно разрешимыми) или нет. Для любой СЛАУ, не являющейся Краме-ровской (переменных больше, чем уравнений), можно указать Крамеровскую СЛАУ (пополнив уравнениями из списка (16)-(18)) с б о льшим значением показателя (11). Поэтому далее рассматриваем только Крамеровские СЛАУ.

Из всего множества Крамеровских СЛАУ выделим те, решение которых удовлетворяет условию (1). Это множество может быть пустым или не пустым. Если это множество пусто, то НМС-набор последовательностей не существует. Если множество однозначных решений, для которых условие (1) выполняется, не является пустым, то все решения – потенциальные претенденты на НМС-набор последовательностей. Для однозначного указания одной из последовательностей достаточно ввести строгое упорядочивание на множестве найденных решений. Именно такое упорядочивание вводит показатель (11), строго упорядочивая все пополненные СЛАУ (включая несовместные и неопределенные). Поскольку отобранные СЛАУ с решениями – их подмножество, то среди них существует единственная СЛАУ, соответствующая максимальному значению показателя в (11). Следовательно, получаемое решение – единственное.

◻

Заме чание 1 . Как видно из приведённого доказательства, СЛАУ (15) первоначально имеет достаточное число уравнений, так как количества уравнений и неизвестных совпадают. Необходимость пополнения СЛАУ возникает только в случае существования линейной зависимости уравнений в СЛАУ, что на практике происходит крайне редко. Автор работы на практике ни разу не сталкивался с ситуацией необходимости пополнения СЛАУ (15). В то же время несовместные СЛАУ (15) встречаются достаточно часто.

Замечание 2 . В том случае, если СЛАУ (15) оказывается неопределённой, существуют различные способы её пополнения. Эти способы зависят от трёх ключевых составляю щи х:

• -    алгебраических свойств данных (обрабатываемых сигналов и изображений);

• -    функциональных свойств данных;

• -    параметров, характеризующих специфику задачи.

• 4.    Процедура построения НМС-набора последовательностей

Как следствие, данное выше определение 5 – это не единственно возможный способ определения

НМС-набора последовательностей². В то же время, для рассматриваемого и наиболее общего случая (рассматриваются последовательности над произвольным коммутативным кольцом K, функциональные свойства данных не используются) данное определение является достаточно простым и универсальным, то есть работоспособным для любого типа данных.

Способ построения НМС-набора последовательностей очевидным образом следует из доказательства теоремы 1. Входными параметрами при построении являются:

• •    тип конструируемого набора ( b , c , d ) ( b , c e F \ { 0 } , d e F ) ,

• •    вектор параметров РЛВРС ( R , M , T , K , a ) ,

• ² Для наиболее распространённого на практике случая, когда используются последовательности над полем вещественных чисел R, альтернативное определение НМС-набора последовательностей для множества отсчётов неоднородности Э может содержать следующие условия:

«... если для значений неоднородности { Ф _г ( m ) } и

L v J (r,m)еЭ последовательностей { hr (m)} r =0Rzi набора выполняют-m =0, M-1

ся условия:

h o* ( 0 ) = 1 ,

ф*r, (M + K -1) = 1

*

r

V

| r : r e { 0,..., R - 1 } &

= min<

[    (r, M + K-1)еЭ

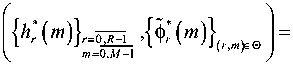
( R -1 M -1

= arg ₍. . min . XX h r ( ^m ) ⁺ X ^ф 2 ( ^m ) .

|{фr (m)}(r,m ),Э "|V r=0 m = 0                (r, m )еЭ l{ hr (m)} r=0R-1 I

В результате так : же получается НМС-набор, для которо-

^ »

го справедливо утверждение Т еоремы 1. Эскиз соответствующего доказательства следующий: множество решений неопределённой СЛАУ (15) образует в пространстве

R ( M + K ) -2

R       выпуклое непустое множество. Тогда искомое решение, то есть вектор с R (M + K)- 2 компонентами

{ ф * ( m ) } „ и { h * ( m ) } , находит-

I ' (r, m )еЭ\{( r, M + K-1)} I ' '^mr, m )es\{(0,0)} ся среди точек этого выпуклого непустого множества, ближайших к началу координат (нулевому вектору). Как известно, множество таких точек состоит из одной точки в силу выпуклости множества [18]. Это гарантирует единственность решения при его существовании, то есть совместности исходной СЛАУ (15).

Недостатком такого альтернативного определения является то, что в общем случае (то есть для последовательностей над некоторым конкретным коммутативным кольцом) оно оказывается математически некорректным.

• •    множество отсчётов неоднородности 0 , удовлетворяющее ограничениям (6) и (14).

Результатом построения является пара множеств:

• •    значений неоднородности { ф * ( m ) }      и

• (r,m)е0

• •    значений отсчётов последовательностей

{ h r ( m ) } r = м—1 ^в наборе.

m =0, M -1

Если построение невозможно, эти множества полагаются пустыми, а ситуация интерпретируется как «ошибка построения». Численная процедура построения НМС-набора последовательностей может быть представлена следующим образом (ниже C 7 - биномиальный коэффициент).

Процедура построения НМС-набора последовательностей

Шаг 1 . Формирование СЛАУ (15). Вычисление рангов расширенной и главной матриц СЛАУ. Если ранги не равны - «ошибка построения». Если ранги равны (и равны некоторой величине R') - переход к шагу 2.

Шаг 2 . Если R'=R ( M+K) , то выполняется решение полученной Крамеровской СЛАУ и вычисление результата (конец процедуры построения). Если R’ <  R ( M + K ) , то переходим к шагу 3.

Шаг 3 . Пополнение СЛАУ (15) уравнениями-равенствами из наборов (16)-(18). Общее количество вариантов пополнения составляет C RM+K 0,| 1 . Для каждого варианта производится вычисление рангов расширенной и главной матриц соответствующей пополненной СЛАУ. Тогда:

• -    если ранги не равны, то выполняется переход к другому варианту пополнения;

• -    если ранги равны и меньше R ( M + K ) , то выполняется переход к другому варианту пополнения (причина - существует вариант пополнения с б о льшим значением показателя (11));

• -    если ранги равны R ( M + K ) , то выполняется решение получившейся Крамеровской СЛАУ. Если в результате решения СЛАУ для получившегося набора последовательностей множество ] 0 [ отсчётов неоднородности удовлетворяет условию (6), то получившийся набор последовательностей - потенциальный претендент на НМС-набор последовательностей. Для него производится расчёт показателя (11).

• 5.    Семейство НМС-наборов последовательностей

Когда все варианты пополнений оказываются исчерпанными, происходит переход к шагу 4.

Шаг 4 . Если список претендентов на НМС-набор последовательностей пуст, то «ошибка построения», в противном случае - среди всех найденных претендентов выбирается тот, для которого показатель (11) имеет максимальное значение. Это и есть результат.

Как уже было отмечено в Замечании 1 , автору настоящей работы на практике ни разу не попадалась неопределённая СЛАУ (15). Поэтому сложная в вычислительном плане часть приведённой процедуры (шаги 3 и 4), связанная с выполнением цикла пополнения СЛАУ и решениями пополненных СЛАУ, на практике обычно не выполняется ни разу.

Замечание 3 . Приведённое описание процедуры отражает лишь принцип построения НМС-набора последовательностей. Наиболее сложную часть, связанную с полным перебором вариантов пополнения СЛАУ на шагах 3 и 4, можно существенно ускорить, применив динамическое программирование [14]. Для этого следует использовать различия «весовых» составляю щи х у слагаемых в показателе (11).

Пусть далее пара параметров ( b , c , d ) удовлетворяет условию b , c е F \ { 0 } , d e F .

Определение 6. ( R , M , T , K , a ) - семейством

НМС-наборов последовательностей типа ( b , c , d ) , обозначаемым p ( bcd ) ( R , M , T , K , a ) , называется множество НМС-наборов последовательностей типа ( b , c , d ) с вектором параметров ( R , M , T , K , a ) .

Из приведённого определения видно, что НМС-наборы последовательностей одного семейства отличаются множествами отсчётов неоднородностей.

Предложение 2 (о количестве НМС-наборов в семействе).

VM > K > 1 R > T > 1

। ^ ( b , c , d ) ^{( R} ’ ^M ’ ^T ’ ^K ’ a )| - ^C R ( M + K ) -1 — ^C R ( M + K -1 )-Г

Доказательство:

Поскольку для множества отсчётов неоднородности НМС-набора последовательностей справедливо соотношение |0| <  KR + 1 и ( 0,0 ) е 0 , то число последовательностей в семействе - это размещение оставши хся RK отсчётов неоднородности среди R ( M + K ) - 1        отсчётов множества

{ ( r , m ) : r = 0, R -1, m = 0, M + K - 1 } , при выполнении условия: 3 r e 0, R - 1: ( r , M + K — 1 ) e 0 _r c 0 .