Эффективные пространственные формы зубьев рабочего инструмента бурильных машин ударного действия

В основу работы, рассматривающей закономерности распространения ударных волн в зубьях ударного инструмента (долота и коронки бурильных машин ударно-поворотного и ударно-вращательного типов, пики и зубила отбойных молотков и т.д.) положен принцип Гюйгенса, описывающий закон отражения волн. Он свидетельствует о том, что «угол отражения волны равен углу падения по отношению к отражающей поверхности» и «падающий луч, луч отраженный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости» [1].

Формы зубьев ударного инструмента могут быть разнообразными (рис. 1) [2, 3, 4]. Процесс прохождения ударных волн в зубьях различной конфигурации может быть различным по характеру, что оказывает определяющее значение на рабочий процесс и, соответственно, на производительность горных машин ударного действия.

Существенное значение на процесс ударного разрушение оказывает форма боковой поверхности инструмента, которая должна быть подобрана таким образом, чтобы ударные волны могли максимально сосредотачиваться в зоне контакта зуба с отбиваемой породой. Поэтому оценить эффективность прохождения ударных волн в пространственной форме зуба целесообразно с помощью коэффициента эффективности боковой поверхности к  .»,=     ,                                (1)

Sбок где Sвх - площадь проекции входных зон на боковой поверхности зуба, характеризующаяся тем, что ударная волна, попавшая в эти зоны, отражаясь один или более раз от стенки в конечном итоге проходит в зону контакта, а затем в породу, мм2; Sбок - площадь проекции боковой поверхности зуба.

Графический анализ распространения ударных волн в зубьях различных форм с треугольным (трапецеидальным) профилем сечения

Эффективность прохождения ударной волны в зубе треугольного (трапецеидального) профиля в горную породу с двумя отражениями вектора от боковой стенки зуба определяется с помощью значения ta исходя из схемы, представленной на рис. 2.

ta = lбок1 sin , мм, где – угол наклона боковой поверхности зуба, °. Здесь lбок1 = lбок – lбок2 – lбок3 – … – lбокN – lбок(N+1), мм.

где l бок – длина боковой поверхности зуба, мм; N – общее количество отражений вектора распространения ударной волны от боковой стенки зуба до попадания в зону контакта t конт

Для N – общего количества отражений вектора распространения ударной волны от боковой стенки зуба до попадания в зону контакта tконт, значения lбок2, lбок3, … , lбок(N+1) будут определяться по следующим формулам lбок N 1

t конт

бок N

tg 2N cos sin t      2 sin l конт              бок N 1

, мм,

, мм, tg 2( N 1) cos sin

бок3

t 2Si sin 5 Д . +... + 1, _Ar. -+1, конт               бок4           бок N 1     бок N

l бок2

tg 4 cos sin t конт +2sin8 1бок 3 + .+ l

, мм,

бок N     l бок N 1

tg2 cos sin

, мм.

Для пирамидальной с четырьмя прямыми гранями формы зуба (поз. 1 на рис. 1) площадь проекции входных зон зуба на ось x составляет:

S _вх = [( T _з – t _пром) – 2 t _a – t _конт] b _конт 2, мм ,

где b конт – ширина зоны контакта ( b конт = t конт ), мм.

Максимальная величина площадь проекции входных зон зуба на ось x составляет:

S _вх.max = [( T _з – t _пром) – t _конт] b _конт 2, мм .

Площадь проекции боковой поверхности зуба на ось x составляет: S б _ок = ( T _з – t _пром) – t _конт , мм .

Подставляя формулы (2), (3), (4) в формулу (1) получаем зависимости коэффициента эффективности боковой поверхности k эфф.бок от величины зоны контакта t конт и угла наклона боковой поверхности зуба для пирамидальной с четырьмя прямыми гранями формы зуба. При этом для зависимости k эфф.бок ( t конт ) необходимо соблюсти условие, что при S вх S вх.max в числитель формулы (1) подставляется выражение (2), а при S вх S вх.max – выражение (3). Графики зависимостей k эфф.бок ( t конт ) и k эфф.бок ( ) для пирамидальной с четырьмя прямыми гранями формы зуба изображены, соответственно, на рис. 3, 4.

Для конусной формы зуба (поз. 2 на рис. 1) площадь проекции входных зон зуба на ось x составляет:

S вх

пром       а           конт         2

, мм .

Площадь проекции боковой поверхности зуба на ось x составляет:

T 22

з    t пром       π t конт         2

S бок              ^р ₄             , мм .

Подставляя формулы (5), (6) в формулу (1) получаем зависимости коэффициента эффективности боковой поверхности kэфф.бок от величины зоны контакта tконт и угла наклона боковой поверхности зуба 8 для конусной формы зуба. При этом необходимо соблюсти условие, что при Sвх Sбок в числитель формулы (1) подставляется выражение (5), а при Sвх Sбок – выражение (6). Графики зависимостей kэфф.бок (tконт) и kэфф.бок (8) для конусной формы зуба изображены, соответственно, на рис. 5, 6.

Для клиновой формы зуба (поз. 3 на рис. 1) площадь проекции входных зон зуба на ось x составляет:

S _вх = [( T _з – t _пром) – 2 t _a – t _конт] B _з, мм , где B з – ширина зуба, мм.

Площадь проекции боковой поверхности зуба на ось x составляет: S б _ок = [( T _з – t _пром)– t _конт] B _з, мм ,

Подставляя формулы (7), (8) в формулу (1) зависимости коэффициента эффективности боковой поверхности k эфф.бок от величины зоны контакта t конт и угла наклона боковой поверхности зуба 8 для клиновой формы зуба. При этом необходимо соблюсти условие, что при S вх S бок в числитель формулы (1) подставляется выражение (7), а при S вх S бок – выражение (8). Графики зависимостей k эфф.бок ( t конт ) и k эфф.бок (8) для клиновой формы зуба изображены, соответственно, на рис. 7, 8.

Графический анализ распространения ударных волн в зубьях различных форм с круглым профилем сечения

Эффективность прохождения ударной волны в зубе круглого профиля в горную породу определяется с помощью критических значений t a. max i и t a. min i , где i – число отражений вектора ударной волны от боковой стенки зуба (для i = 1 смотри схему на рис. 9). Значения t a. max i и t a. min i вычисляются по следующим формулам:

где r – радиус зуба, мм; углы ос max i и осmin i (см. рис. 11) находятся из выражений а .

max i

2 i +1

t

— + arcsin конт

2         2 r )

а . .

min i

2 i +1

t arc s in конт

2         2 r )

С увеличением количества отражений ударной волны от стенки i уменьшается длина хорды (отрезка вектора между отражениями). На рис. 9 это отрезки AF и BE . Обозначим эти отрезки как длина хорды L х. i . При условии, что L х.max. iN ≤ t конт , все ударные волны будут попадать в зону контакта. Здесь iN – количество отражений ударной волны от боковой стенки зуба при выполнении условия.

Длина хорды L х.max .i , L х.min .i определяется по формуле

L _{х.max .i} = 2 r        , L _х.m i _{n .i} = 2 r ₂    , мм.

Определим общую длину входных зон фронта ударной волны, при которых векторы их распространения попадают в зону контакта t конт , отражаясь по пути распространения от боковой стенки зуба 1, 2 … N раз, по формуле T бок.акт = ( t a.max 1 – t a.min 1 ) + ( t a.max 2 – t a.min 2 ) +… + ( t a.max N –1 – t a.min N –1 ) + t a.max N , мм, где значения t a. max1 , t a. min1 , определённые по формулам (9), действительно в диапазоне изменения величины зоны контакта от 0 до t конт.крит1 ; для t a. max2 , t a. min2 этот диапазон составит от 0 до t конт.крит2 ; для t a. max i , t a. min i (формула (9)) – от 0 до t конт.крит i ; для t a. max M ,   t a. min M – от 0 до t конт.крит M . Здесь t конт.крит1 = L хорда.max1 ;

t конт.крит2 = L хорда.max2 ; t конт.крит i = L хорда.max i ; t конт.крит M = L хорда.max M .

Для пирамидальной с четырьмя круговыми гранями формы зубьев (поз. 3 на рис. 1) площадь проекции входных зон зуба на ось x составляет несколько участков:

– t a.min i –1 ) + 4 t конт t a.max i , мм , (12) где i – количество отражений вектора распространения ударной волны от боковой стенки зуба до попадание в зону контакта t конт .

Значение S вх1 , определённое по формуле (10), действительно в диапазоне изменения величины зоны контакта от 0 до t конт.крит1 , для S вх2 (формула 11) этот диапазон составит от 0 до t конт.крит2 , для S вх i (формула 12) этот диапазон составит от 0 до t конт.крит i .

С помощью формул (10) – (12) нельзя рассчитать значение площади проекции входных зон зуба на ось x в нулевой зоне, т.е. в диапазоне изменения величины зоны контакта от t конт.крит1 до t конт.max , где t конт.max = 2 ∙ r . Этому диапазону будет соответствовать такая форма зуба, при которой все ударные волны, попавшие на боковую поверхность, отразятся в зону t конт . В этом случае площадь проекции входных зон зуба на ось x в нулевой зоне составит

S _вх0 = [( T _з – t _пром) – t _конт] b _конт 2, мм².

График зависимости коэффициента эффективности боковой поверхности k эфф.бок от величины зоны контакта t конт для пирамидальной с четырьмя круговыми гранями формы зубьев изображены, соответственно, на рис. 10.

Для сферической формы зубьев (поз. 5 на рис. 1) площадь проекции входных зон зуба на ось x составляет несколько участков:

π

^S вх1

пром

‘ -It пром       а

s , =

вх2

пром       а.min1

, мм2.

пром       а.max1

пром

Tt       ²

з    пром       а.max2           2

, мм .

S вх i

пром       а.min1

пром       а.max1

пром       а.min2

пром       а.max2

π

пром        а.min i 1

пром        а.max i 1

пром

з    пром       а.max i           2

, мм .

где i – количество отражений вектора распространения ударной волны от боковой стенки зуба до попадание в зону контакта t конт .

Значение S вх1 , определённое по формуле (13), действительно в диапазоне изменения величины зоны контакта от 0 до t конт.крит1 , для S вх2 (формула 14) этот диапазон составит от 0 до t конт.крит2 , для S вх i (формула 15) этот диапазон составит от 0 до t конт.крит i .

С помощью формул (13) – (15) нельзя рассчитать значение площади проекции входных зон зуба на ось x в нулевой зоне, т.е. в диапазоне изменения

величины зоны контакта от t конт.крит1 до t конт.max , где t

π

S вх0 = + —

пром        конт

конт.max = 2 ∙ r . В этом случае 2

, мм2.

График зависимости коэффициента эффективности боковой поверхности k эфф.бок от величины зоны контакта t конт для сферической формы зубьев изображены, соответственно, на рис. 11.

Для полуцилиндрический формы зубьев (поз. 6 на рис. 1) проекции входных зон зуба на ось x составляет несколько участков:

площадь

a.max i , мм ,

a.min 2 ) + …+ 2

где B з – ширина зуба, мм, i – количество отражений вектора распространения ударной волны от боковой стенки зуба до попадание в зону контакта t конт .

Значение S вх1 , определённое по формуле (16), действительно в диапазоне изменения величины зоны контакта от 0 до t конт.крит1 , для S вх2 (формула 17) этот диапазон составит от 0 до t конт.крит2 , для S вх i (формула 18) этот диапазон составит от 0 до t конт.крит i .

С помощью формул (16) – (18) нельзя рассчитать значение площади проекции входных зон зуба на ось x в нулевой зоне, т.е. в диапазоне изменения величины зоны контакта от t конт.крит1 до t конт.max , где t конт.max = 2 ∙ r . В этом случае

S вх0 = [( T з – t пром ) – t конт ] B з , мм²,

График зависимости коэффициента эффективности боковой поверхности k эфф.бок от величины зоны контакта t конт для полуцилиндрический формы зубьев изображены, соответственно, на рис. 12.

Выводы

Проведённый анализ в статье показывает, что эффективность прохождение ударных волн в зубе инструмента будет возрастать в зависимости от увеличения величины зоны контакта t конт , связанного с износом рабочей поверхности. Проведённые эксперименты показывают, что эффективность процесса ударного процесса разрушения действительно повышается в связи с увеличением зоны контакта, но до определённого значения. Выше этого значения начинает снижаться эффективность рабочего процесса из-за ухудшения условий контакта инструмента с горной породой.

На производительность процесса ударного разрушение определяющее значение оказывает форма зубьев инструмента, которая должна максимально сосредотачивать ударные волны в зону контакта зуба с отбиваемой породой.

Анализ полученных зависимостей коэффициента эффективности боковой поверхности k эфф.бок от величины зоны контакта t конт показывает, что самой эффективной пространственной формой зуба по критерию прохождения ударных волн в породу является клиновая (поз. 3 на рис. 1). Для этой формы характерен интенсивный процесс сосредоточения ударных волн в зону контакта. Причём в начальной стадии притупления инструмента (примерно до 1 мм), как видно из рис. 7, ударные волны с высокой эффективностью проходят в зону контакта t _конт.

К высокоэффективным формам по указанному критерию можно отнести также сферическую и конусную (поз. 5 и 2 на рис. 1), но в меньшей, чем клиновую. Полуцилиндрический зуб является достаточно эффективным.

Для сферической формы зуба характерен не очень интенсивный процесс сосредоточения ударных волн в зону контакта, но в начальной стадии притупления инструмента (примерно до 1 мм), как видно из рис. 11, ударные волны с высокой эффективностью проходят в зону контакта t конт .

Для конусной формы зуба характерно очень высокое сосредоточение ударных волн в зону контакта, но в начальной стадии притупления инструмента (примерно до 1 мм), как видно из рис. 5, ударные волны плохо проходят в зону контакта t конт .

Для полуцилиндрической формы зуба характерно не очень высокое сосредоточение ударных волн в зону контакта, а в начальной стадии притупления инструмента (примерно до 1 мм), как видно из рис. 12, ударные волны достаточно эффективно проходят в зону контакта t _конт.

Низкоэффективными формами зубьев являются пирамидальный зуб с четырьмя прямыми гранями (поз. 1 на рис. 1) и пирамидальный зуб с четырьмя круговыми гранями (поз. 4 на рис. 1) из-за наличия мёртвых зон для ударных волн (рис. 13 и 14). Волны, попавшие в мёртвую зону, не проходят в зону контакта. Поэтому сосредоточение ударных волн в зону контакта невысокое. Причём в начальной стадии притупления инструмента (примерно до 1 мм), как видно из рис. 3 и 10, ударные волны практически на проходят в зону контакта t конт .

Анализ полученных зависимостей коэффициента эффективности боковой поверхности к эфф.бок от угла наклона боковой поверхности зуба 5 на рис. 4, 6 и 8 показывает, что высокоэффективной пространственной формой зуба трапецеидального сечения по критерию прохождения ударных волн является клиновая (поз. 3 на рис. 1), менее эффективной формой является конусная, низкоэффективной - пирамидальный зуб с четырьмя прямыми гранями из-за наличия мёртвых зон.

На графиках цифрами с 1 по 8 показаны зоны с максимально возможным отражением ударной волны от боковой поверхности зуба равным: одному в зоне под цифрой 1 , двум в зоне под цифрой 2 и т.д. В зоне под цифрой 8 максимальное количество отражение может составлять 8, 9, 10 и более раз.

Также графики к _эфф . _бок (5) показывают, что эффективность прохождение ударных волн в зубе с уменьшением угла наклона боковой грани резко возрастает (на графиках к _эфф . _бок (8) в диапазоне от 20° до 10°). В области критических углов (на графиках к _эфф . _бок (8) около 10°) происходит высокое сосредоточения ударных нагрузок в зоне контакта, что вызывает напряжения в материале зуба, превышающие предел прочности. При этом происходит выкрашивание участков зуба в зоне контакта с породой. В данном случае необходимо перед началом использования рабочего инструмента создавать зону притупления на зубе не менее 2 + 3 мм.

Проблема выкрашивания участков зуба в зоне контакта с породой не существует у зубьев кругового сечения, но эффективность прохождения ударных волн в зону контакта у таких зубьев значительна меньше, чем у зубьев трапецеидального сечения.

Не рекомендуется использовать шиповую и вогнуто-клиновую формы зубьев (поз. 7 и 8 на рис. 1) для ударной отбойки полезного ископаемого. При этом рабочий процесс будет сопровождаться интенсивным выкрашиванием участков зуба в зоне контакта с породой. Эффективность прохождения ударных волн в зону контакта у шиповых и вогнуто-клиновых зубьев низкая.

Эффективность прохождения ударных волн в сферо -конической и клиновой скруглённой формах зубьев сопоставима со сферической и полуцилиндрической формами зубьев.

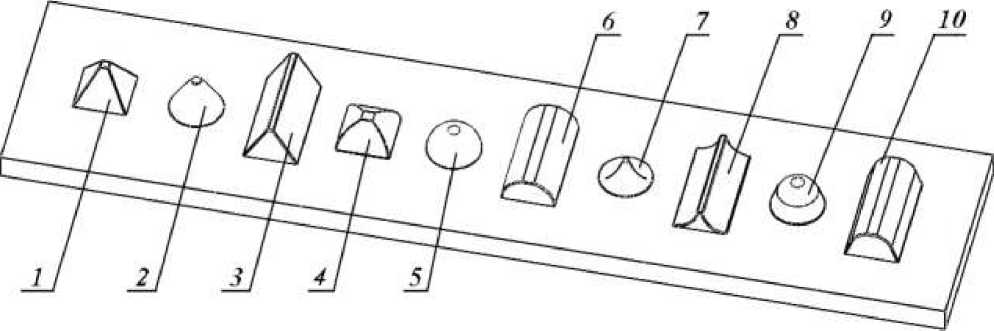
Рис. 1. Основные формы зубьев ударного инструмента:

1 – пирамидальная с четырьмя прямыми гранями, 2 – конусная, 3 – клиновая, 4 – пирамидальная с четырьмя круговыми гранями, 5 – сферическая, 6 – полуцилиндрический, 7 – шиповая, 8 – вогнуто-клиновая, 9 – сферо-коническая, 10 – клиновая скруглённая.

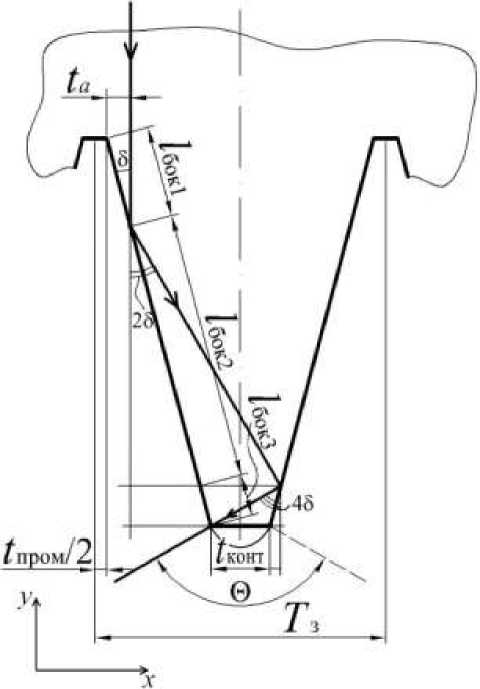
Рис. 2. Схема вектора распространения фронта ударной волны на отдельном участке с двумя отражениями от боковой стенки зуба трапецеидального профиля:

l бок1 , l бок2 , l бок3 – отрезки на боковой поверхности зуба располагающиеся между точками, соответственно, основания зуба и первого отражения, первого и второго отражения, второго отражения и прохождения волны в породу;

Θ – максимальный угол прохождения волны из зуба в породу;

T з – длина зуба

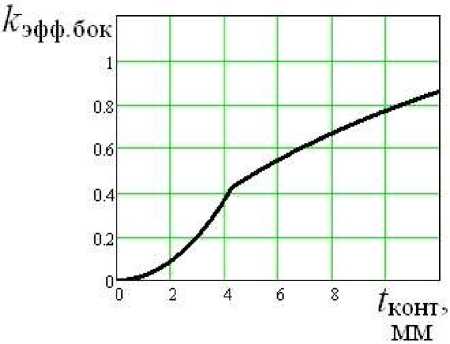
Рис. 3. Зависимость коэффициента эффективности боковой поверхности пирамидального с четырьмя прямыми гранями зуба от величины зоны контакта.

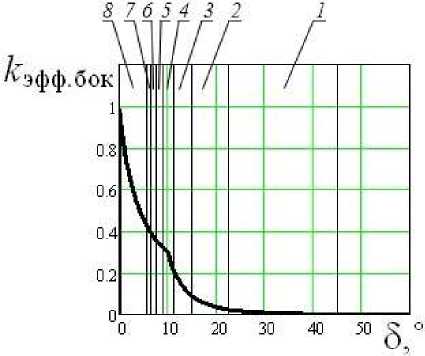
Рис. 4. Зависимость коэффициента эффективности боковой поверхности пирамидального с четырьмя прямыми гранями зуба от угла наклона боковой поверхности зуба.

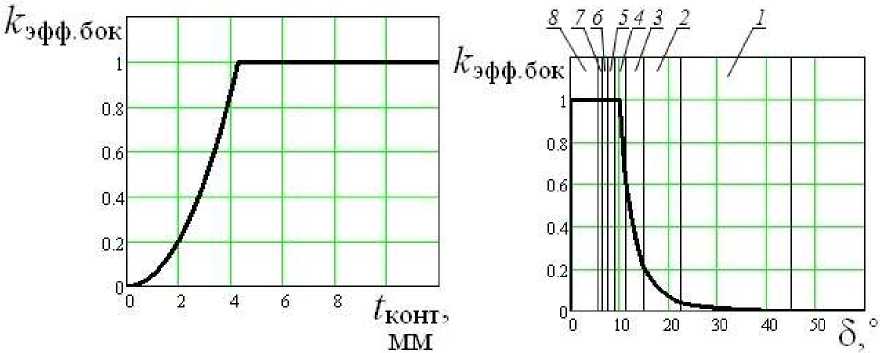
Рис. 6. Зависимость коэффициента эффективности боковой поверхности конусного зуба от угла наклона боковой поверхности зуба.

Рис. 5. Зависимость коэффициента эффективности боковой поверхности конусного зуба от величины зоны контакта.

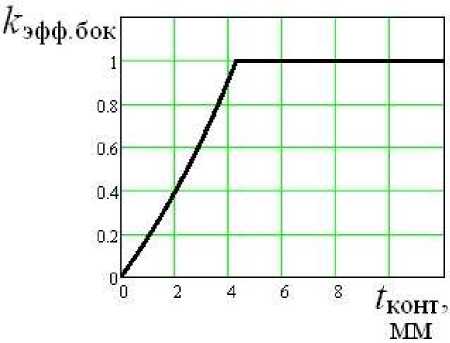
Рис. 7. Зависимость коэффициента эффективности боковой поверхности клинового зуба от величины зоны контакта.

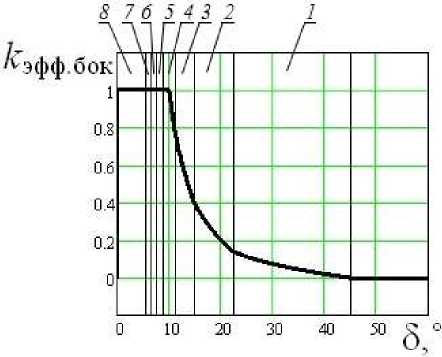
Рис. 8. Зависимость коэффициента эффективности боковой поверхности клинового зуба от угла наклона боковой поверхности зуба.

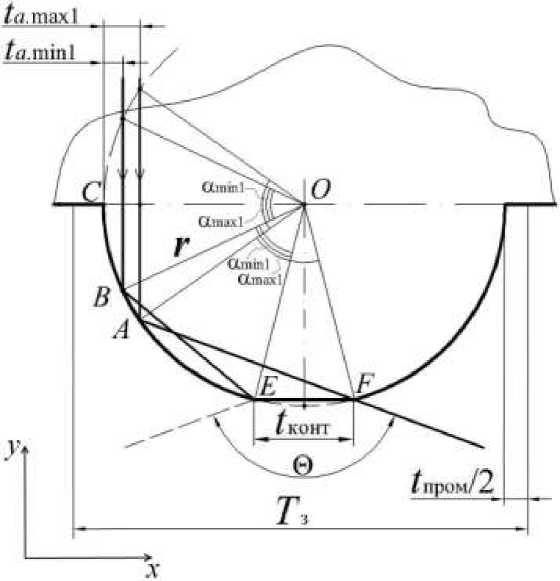
Рис. 9. Схема векторов распространения фронта ударной волны с одним отражением от боковой стенки зуба с круговым профилем при критических значениях t a. max1 и t a. min1

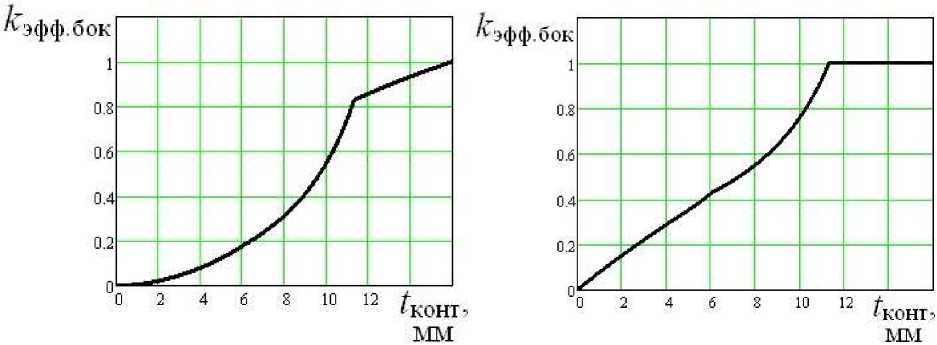
Рис. 10. Зависимость коэффициента эффективности боковой поверхности пирамидального с четырьмя круговыми гранями зуба от величины зоны

Рис. 11. Зависимость коэффициента эффективности боковой поверхности сферического зуба от величины зоны контакта.

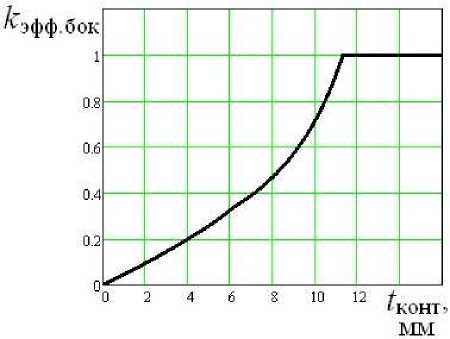
Рис. 12. Зависимость коэффициента эффективности боковой поверхности полуцилиндрического зуба от величины зоны контакта.

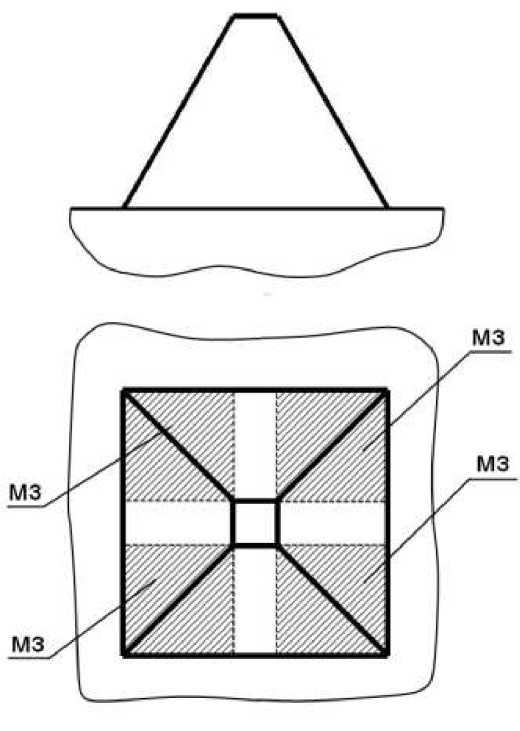
Рис. 13. Схема мёртвых зон распространения ударных волн для пирамидального зуба с 4-мя прямыми гранями

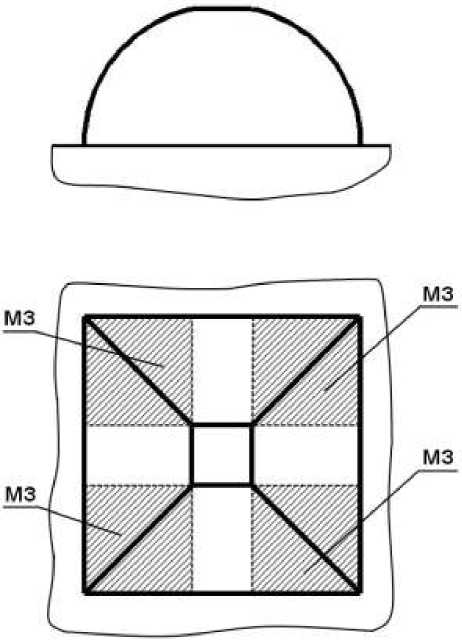
Рис. 14. Схема мёртвых зон распространения ударных волн для пирамидального зуба с 4-мя круговыми гранями

The description of the basic forms of teeths of a shock instrument is given. The geometrical analysis of distribution of shock waves in a shock instrument is carried out. On the basis of this analysis conclusions are drawn on efficiency of use of various forms of teeths.