Эффективные упругие модули тканого композита полотняного плетения с локальными технологическими дефектами

Тканые композиты с поликристаллической матрицей получили широкое распространение в авиационной и космической промышленности. Из таких материалов изготавливают несущие панели крыла, оперения и фюзеляжа самолетов, лопатки турбин, сопловые блоки, носовые обтекатели ракетных двигателей, уплотнительные элементы для трубопроводов гидро- и пневмосистем и многие другие элементы конструкций, эксплуатируемые в условиях интенсивного теплового (или криогенного) и механического воздействия [1]. Отличительной особенностью процесса изготовления готовых изделий из этих материалов является раскрой и выкладка на оправку слоев ткани с искривленными волокнами (полотняной, сатиновой, саржевой и др.), а также прошивка этих слоев между собой. Полученный армирующий каркас насыщается поликрис-таллической матрицей, в результате чего происходит одновременное создание самого элемента конструкции и материала, из которого он изготовлен.

При производстве изделий из тканых композитов неизбежны технологические дефекты, снижающие эксплуатационные свойства изделий. К числу типичных локальных дефектов относятся пропуск волокон основы или утка,

разрывы нитей армирующего каркаса при прошивке слоев, которые обнаруживаются только на этапе выходного ультразвукового контроля элементов конструкций. Гарантированное обеспечение наличия в этих участках поликристал-лической матрицы (при осаждении из газовой фазы или при карбонизации полимеров после пропитки под давлением, вакуумирования и до-уплотнения армирующего каркаса), матрицы на основе терморасширенного графита (после прокатки слоев фольги) или керамики затруднено [2]. Это связано с тем, что образующиеся на поверхности нитей слой осаждаемого материала препятствует дальнейшему насыщению каркаса.

Применение тканых композитов для изготовления элементов конструкций ответственного назначения, работающих в условиях многократно изменяющихся внешних нагрузок в течение длительного срока эксплуатации, предопределяет необходимость прогнозирования эффективных упругих свойств. В настоящей статье представлены результаты оценки влияния сложной геометрии армирующего каркаса и локальных технологических дефектов на эффективные модули Юнга и коэффициенты Пуассона слоя композита полотняного плетения (саржа 1/1 с равными рапортами по основе и утку), которые были получены при помощи разработанной ранее двухуровневой модели тканого материала с искривленными волокнами и поликристалличе-ской матрицей [3-5]. Выбор полотняного переплетения обеспечил наиболее короткие перекрытия нитей, наибольшую прочность, плотность и повышенную жесткость, однородную, геометрически идентичную с лицевой и изнаночной стороны поверхность ткани.

Исследовался слой тканого композита толщиной 2,5 D с армирующим каркасом полотняного переплетения, образованного волокнами круглого поперечного сечения постоянного диаметра D . Следуя [3-6], искривление волокон основы и утка ткани описывалось дугой окружности с центральным углом а =п/4 и участком прямой. В силу малости деформаций предполагалась неизменность углов а при нагружении слоя.

Построение геометрической модели было осуществлено с использованием препроцессора, входящего в состав платформы SALOME-MECA, предназначенной для решения задач механики сплошных сред, термо- и гидродинамики, акустики и магнетизма, выполнения расчетов для строительных конструкций и сооружений [7]. На рис. 1 представлены фрагменты слоя тканого композита с коэффициентами армирования а i = а ₃=0,14. Здесь и далее оси x ₁ и x ₃ ортогональной декартовой системы координат будут принадлежать плоскости слоя.

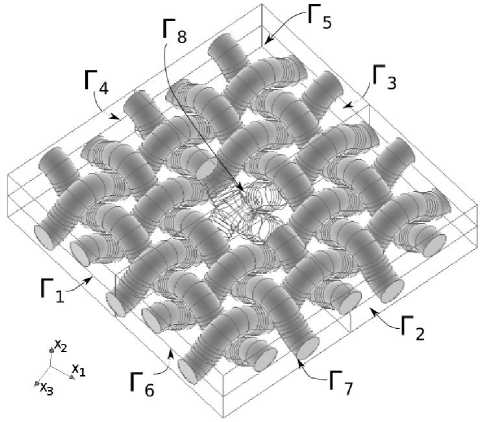
Рис. 1. Фрагмент слоя тканого композита полотняного плетения с локальным технологическим дефектом в виде локального разрыва нитей сно-вы и утка

Были рассмотрены наиболее типичные локальные технологические дефекты: полости, связанные со случайными разрывами основы или основы и утка (рис. 1), которые появляются при сшивке слоев, но могут присутствовать в исходной ткани до прошивки. Размеры рассматриваемых дефектов были соизмеримы с характерными размерами неоднородностей, не изменяли значительно интегральные коэффициенты армирования композита, могли быть частично или полностью заполнены материалом матрицы. Волокна и матрица слоя тканого композита предполагались изотропными, линейно упругими, не изменяющими геометрию, взаимное расположение и тип симметрии при нагружении. Поэтому компоненты тензора напряжений oi(г)удовлетворяли уравнениям равновесия, а компоненты тензора малых деформаций ey(r) были связаны с компонентами вектора перемещений ui(r) соотношениями Коши

ау,•(r)= 0    2еj(r)= Uj(r) + uj,i(r)

Описание геометрии слоя тканого композита проводилось при помощи единичной, кусочно-однородной индикаторной функции X( r ) радиус-вектора г , принимавшей значение 1, если точка принадлежала волокнам основы или утка и 0, если матрице. Это позволило записать определяющие соотношения следующим образом:

° у( r )=№Щ )+Cm [1-X(r)]}s ki (r), р)

где верхними индексами f и m отмечены материальные коэффициенты, которые относились к нитям армирующего каркаса и матрице соответственно.

Краевая задача (1)-(2) была дополнена условиями симметрии:

u3 (r )k = u1 (r   = u2 (r)Г = 0     ПА

,        (3)

^ 12 ^{( r})1 г₄ = ° 23 ^{( r} )1 г₄ = ^С 12 ⁽ r⁾l r₃^=а 13 ^{( r})1 _Гз = ⁰ ,

° 12 ^{( r} )1г₅ =^Q 13 ⁽ r )1г₅ =^П 12 ⁽ r ⁾1 г₆ =° 13 ⁽ r ⁾1г₆ = ⁰

и условиями идеального сопряжения

[^j(r) nj (r '  ,.    '<(r) nj(r )]|r-

[ui (r)!r+=[ui (r)lr- на границах раздела фаз Г7 (рис. 1), на которых предполагалось отсутствие химических реакций и фазовых переходов в процессе нагружения слоя. Равенства (4) позволили описать совместную работу нитей и поликристаллической матрицы при нагружении.

Полости, образованные при пропуске или разрыве нитей армирующего каркаса (рис. 1), моделировались исключением локальных объемов искривленных волокон. Точки образовавшейся внутренней поверхности Г ₈ не имели ограничений на перемещения, а сама поверхность была свободна от напряжений:

[a ,j ^{( r} ) n j ^{( r} ) ]|_г$= ⁰

Дополняя равенства (3)-(5) условиями:

• ^U 1 ^{( r})l r₂ = ^{£ ;} 1 ^r1    ^u 2 ⁽ r)l r₅ = ^{0     U} 3 ^{( r} )1 г_х = ⁰

,                                           ,                                           ,

• ^u 3 ( ^r )1_П = ^£ 33 ^r 3     ^U 2 ^{( r} )1г₅ = ^{0     U} 1 ^{( Г} )1г₂ = ⁰

,                                            ,                                           , которые обеспечивали заданное макроскопически однородное одноосное деформирование в направлениях x1 и x2 соответственно (при £22 = 0), можно было определить эффективные модули Юнга Е^ и коэффициенты Пуассона v ij из решения систем уравнений:

*

^£ 11 =

Е;(

*

^О 11

—

*

^£ 22 =

—

*

А2 ^ц+

Е 1

*

*

*

^v 12 ° 22

^v 13 ^G 33 )

,

*

*

л (

Е

*

*

^О 22

^-v 12 ° 33 )

,  (8)

*

^£ 33 =^-v 23 Ц ^О 11 + Ц ^О 22

*

Е 1

Е 2

+ Ат О33Е3  33

,

предполагая, что слою тканого композита соответствовала однородная ортотропная среда. Здесь £ ij и О ij - компоненты тензоров макродеформаций и макронапряжений, которые являлись заданными или вычисленными в результате усреднения по объему рассматриваемого фрагмента слоя тканого композита.

Численное решение краевой задачи (1)-(2) с граничными условиями (3)-(6) или (3)-(5), (7) проводилось методом конечных элементов с помощью некоммерческого пакета Code-Aster, входящего в состав платформы SALOME-MECA [7]. Степень дискретизации фрагментов на 16-узловые тетраэдральные и 20-узловые гексаэд-ральные изопараметрические элементы выбиралась таким образом, чтобы полученные в результате численного решения поля структурных перемещений, деформаций и напряжений в слое тканого композита без локальных дефектов и с несовершенствами ни качественно, ни количественно не изменялись при уменьшении характерных размеров конечных элементов. Этим результатам соответствовали сетки с не менее, чем 78000 20-узловых гексаэдральных и 406000 16-узловых тетраэдральных элементов.

В табл. 1 представлены эффективные упругие свойства слоя тканого композита с поликри-сталлической матрицей, прогнозирование которых для фрагментов с различными локальными технологическими дефектами было осуществлено при следующих свойствах фаз: E f =280 ГПа ГПа и v f =0,20 (модуль Юнга и коэффициент

Пуассона материала нитей армирующего каркаса) [8], E m =0,28 ГПа и v m =0,40 (модули поликри-сталлической матрицы.

При определении эффективных свойств возникла необходимость интегрирования по объему изменяющихся внутри конечных элементов полей структурных напряжений и деформаций для вычисления соответствующих макроскопических значений, входящих в систему уравнений (8). Поскольку эта операция не предусмотрена пакетом Code-Aster [7], был разработан и программно реализован модуль расширений платформы SALOME-MECA на языке Python. Интегрирование методом Гаусса-Лежандра по объему 20-узловых гексаэдральных изопараметрических элементов производилось по 8 точкам, а 10-узловых тетраэдральных конечных элементов – по 5 точкам, координаты которых, весовые коэффициенты, а также функции формы соответствовали работам [7, 9]. Для увеличения производительности в разработанном модуле интегрирования было предусмотрено выполнение параллельных вычислений с использованием нескольких процессоров. Многопроцессорность была достигнута с помощью пакетов Parallel Python и MPI4PY, продемонстрировавших одинаковые результаты линейного кратного уменьшения временных затрат на проведение операций с плавающей точкой. Так, например, использование 4 процессоров позволило сократить время вычисления значений компонент тензоров макронапряжений и макродеформаций в 4 раза.

Результаты прогнозирования эффективных упругих модулей (табл. 1) показали существенное влияние на искомые величины (по сравнению с материалом идеальной периодической структуры) локальных технологических дефектов. Так, например, обнаружено существенное (до 13 раз) снижение модуля Юнга Е₂ в направлении оси x 2 , перпендикулярной плоскости слоя, и уменьшение в 3 раза модулей Е^ в направлении x 1 , совпадающем с направлением пропущенной нити основы. Вместе с тем, наличие в тканом композите локального разрыва волокон основы или основы и утка лишь в 1,25 раза снижают эффективные модули Е^ и Е₃ в плоскости слоя.

Дополнительное насыщение материалом матрицы полости, возникающей на месте пропуска волокна или разрыва нитей, как показали ранее полученные результаты [3-5], привело локальному изменению (на масштабах, соизмеримых с характерным размером волокон) симметрии армирующего каркаса и, как следствие к

существенному снижению коэффициентов концентрации напряжений и смене механизмов разрушения. Однако значительного изменения эффективных модулей Юнга и коэффициентов Пуассона не наблюдалось. Этот неожиданный результат может быть объяснен тем, что упругие модули фаз армирующего каркаса и поликри-сталлической матрицы у исследуемого материала различались на два порядка.

Таблица 1. Эффективные упругие модули тканого композита с локальными технологическими дефектами

Тип локального дефекта	* E 1 , ГПа	* E 2 , ГПа	F * E 3 , ГПа	ν 12	ν 13	ν 23
идеальная периодическая структура	167,686	125,679	167,675	0,447	0,016	0,033
	52,609	9,594	132,611	0,378	0,003	0,034
пропуск волокна основы	54,214	11,842	132,215	0,465	0,004	0,034
	135,057	9,391	165,202	0,279	0,003	0,027
разрыв волокна основы	135,200	15,919	166,059	0,470	0,005	0,027
разрыв волокон основы и	135,124	10,171	135,130	0,411	0,006	0,034
утка	135,807	11,351	135,811	0,465	0,002	0,035

Примечание: внутренняя полость, образованная дефектом, остается незаполненной (числитель) или заполняется материалом матрицы (знаменатель)

Проведено исследование влияния масштабного эффекта на значения эффективных упругих модулей слоя тканого композита полотняного плетения на основе численного решения краевых задач для различных фрагментов материала, которые содержали один (рис. 1), два и три слоя окружающих локальные технологические дефекты ячеек, образованных переплетением нитей основы и утка. Результаты вычислительных экспериментов показали, что включение в геометрическую модель второго слоя ячеек позволяет уточнить результаты прогнозирования эффективных характеристик на 3,5 %, а третьего слоя – еще на 1,5%.

Выводы: концентрация (количество разрывов или пропусков нитей) отдельных локальных технологических дефектов, находящихся на расстоянии, как минимум, двух-трех характерных размеров ячеек, образованных переплетением нитей армирующего каркаса, в элементе конструкции, изготовленном из тканого композита, не является ключевым фактором, существенно влияющим на значения эффективных упругих модулей, однако предопределяющим сценарии развития процесса разрушения.

Исследования проведены в рамках задания № 2014/152 на выполнение государственных работ в сфере научной деятельности в рамках базовой части госзада-ния Минобрнауки РФ (код проекта – 1911).