Эффективный алгоритм определения истинности утверждений о действительных числах в сигнатуре отношений порядка

Многие практические приложения теоретической информатики могут быть сформулированы в виде некоторого утверждения P ( x 1 , ..., x n ), которое, в зависимости от значений набора переменных, выдаёт результативный ответ ( И или Л ). Естественно, что на содержательном уровне нас интересует не сама постановка задачи как таковая, а существование алгоритма, устанавливающего истинность предиката P , т.е. проблема разрешимост и предиката [2].

Имеется множество примеров разрешимости формальных систем [2]. В частности, алгоритмически разрешима проблема проверки истинности любого утверждения про конечное число вещественных чисел с отношениями равенства и порядка [3]. Как известно, первый такой алгоритм предложил А. Тарский в 1948 году. Однако алгоритм Тарского оказался настолько неэффективным, что практически воспользоваться им невозможно.

В данной работе предлагается новый, более эффективный алгоритм проверки истинности утверждений, заданных на множестве действительных чисел в сигнатуре отношений порядка, сводящийся к решению оптимизационной задачи.

Следует отметить, что под эффективностью здесь понимается не достижение полиномиальной сложности алгоритма, а возможность его практического использования для решения широкого круга прикладных задач. Естественно, что сложность такого алгоритма должна быть меньше экспоненциальной.

В качестве практически значимого примера использования предложенного алгоритма можно привести широкий круг задач, связанных с верификацией вычислительных программ, т.е. программ, реализующих вычислительные методы.

1.    Постановка задачи

Рассмотрим утверждения исчисления предикатов первого порядка с сигнатурой, включающей отношения порядка. Более точно рассмотрим сигнатуру, содержащую предикаты =, <, <, >, >, ^ , арифметические операции и аналитические функции над действительными числами. Предикаты и операции пони- маются естественным образом. В этом случае произвольный предикат можно представить в виде:

P ( X ) = f ( X ) 6 0,                            (1)

где 6 - любое из перечисленных выше отношений порядка, f ( X) - аналитическая функция (алгебраическая или трансцендентная или их комбинация), X = ( x 1 ,..., x n ) ‘ - переменные предиката.

Поставим задачу разработки эффективного алгоритма определения истинности замкнутой формулы, т.е. формулы, не имеющей свободных параметров. Например, аксиомы порядка:

V x V у ⁽⁽⁽ x <  у ) л ⁽ у <  x )) ^ ⁽ x = у )).

2.    «Решающая» функция

Каждому предикату (1) можно поставить в соответствие множество вида:

M _e = { X | f ( X ) 6 0}.

В качестве базисных отношений порядка выберем отношения <  и <. Очевидно, что через базисные отношения можно выразить все остальные отношения порядка:

P > = P < ,

P > = P < ,

P = = Р < л P < ,

P , = P < v P < .

Введём функцию ф ( X) = - f ( X) и через неё определим дополнение базисных множеств соответствующих базисных отношений:

M < = { X | ф ( X ) <  0} и M < = { X | ф ( X ) <  0}.

Между логическими операциями над предикатами и теоретико-множественными операциями над множествами существует очевидная связь:

P ( X ) ^ { X|f ( X ) <  0} = { X | ф ( X ) <  0} { X|f ( X ) <  0} = { X | ф ( X ) <  0},

P ( X ) л Q ( X ) - { Xf ( X ) <  0} I { Xf ( X ) <  0},

P ( X ) v Q ( X ) ^ { X I f_p ( X ) <  0} U { X I f_Q ( X ) <  0}.

Для описания логических операций над предикатами введём «решающую» функцию F ( X) [1]. Для этого первоначально определим «индикаторные» функции следующим образом:

• 1)    для отношения <

J ^{1 если} (XX ) > °’ в< ( X ) = л

[ ° если fXX ) <  °;

• 2)    для отношения <

J ^{1 если f}XX ) >  °’ в/ ( X ) = л

[ ° если fXX ) <  °.

Тогда для логической операции конъюнкции «решающую» функцию можно определить следующим образом:

• F , ( X ) = ( в p f p +в Q f Q )/( в P +в Q +в P e Q ) +

+ Р P в Q ( f p + f Q )/2.

В формуле (7) подразумевается, что индикаторные функции (5)-(6) и функции f p и f Q зависят от X .

«Решающую» функцию для операции дизъюнкции определим так:

F (X) = (в pfp +в QfQ )/(в p + eQ +в p в Q ) +

+ в p в Q ( f p + f Q )/2.                    ^U

«Решающая» функция атомарных формул, использующих базисные отношения ( p < ( X) = f ( X) <  ° или p < ( X) = f ( X) < °), определяется простым выражением:

F ( X ) = f ( X ).

Тогда решающую функцию для операции отрицания можно определить следующим образом: p < = p > ф ( X) <°, откуда F ( X) = - f ( X) . Аналогично для отношения строгого порядка <:

p < = p > = ф ( X) < °, и в результате F ( X) = - f ( X) .

Далее нам потребуется понятие интерпретации формулы. Определим это понятие так, как это сделано в работе [2].

Оценкой п назовём отображение, которое ставит в соответствие каждой индивидуальной переменной некоторый элемент множества, являющийся носителем интерпретации. Этот элемент будем называть значением переменной при данной оценке и обозначать [ x ]( п ). Значение атомарной формулы p ( x 1 ,..., x n ) определим как [ p ]([ x 1 ]( п ),...,[ x n ]( п )). Для логических операций справедливо:

[ p ]( п ) = [ p ( п ),

• [    p Л Q ]( п ) = [ p ]( п ) Л [ Q ]( п ),

• [    p v Q ]( п ) = [ p ]( п ) v [ Q ]( п ),

где p и Q - формулы.

Очевидно, что атомарные формулы p < ( X) (или p _< ( X )) истинны для тех оценок интерпретации переменных, для которых «решающая» функция F ( X) <  ° (или <) °.

Теорема 1 . Формула P л Q, связывающая предикаты, использующие базисные отношения, истинна тогда и только тогда и для тех оценок интерпретации переменных формулы, для которых «решающая» функция (4) меньше или равна нулю.

Доказательство. Несложно показать, что для логической операции конъюнкции, если хотя бы один из предикатов использует отношение < , то p л Q о { X | F ( X) < ° } . В противном случае p л Q о ; XIF ( X) < ° } . Пусть p o {X | f_p ( X) < ° } , а Q o {XIf Q ( X) < ° } .

«Решающая» функция (4) по построению предполагает четыре варианта интерпретации переменных:

• 1)    [ X] ( п 1 ): p ( X) = 1, Q ( X) = °. Из чего следует, что в _p =°, в Q = 1, но тогда F _Л ( X) = f Q . Из чего следует, что для оценки п 1 F _Л ( X) >°.

• 2)    [ X] ( п ₂): p ( X) = °, Q ( X) = 1. Для этой оценки в _p = 1, в Q = ° и F _Л ( X) = f_p . Из чего следует, что для оценки п ₂ F _Л ( X) > °.

• 3)    [ X] ( п ₃): p ( X) = °, Q ( X) = °. Для этой оценки в _p = 1, в Q =1 и F _Л ( X) = (f_p + f Q )/2, но поскольку f p >° и f q >  °, то для оценки п ₃ справедливо F л ( X ) >°.

• 4)    И наконец, существует оценка [ X] ( п ₄): p ( X) = 1, Q ( X) = 1, для которой в _p = °, в Q = °. В этом случае F _Л ( X) = (f_p + f Q )/2, но поскольку f p <  ° и f q <  °, то для оценки п ₄ F _Л ( X) <  °.

Но тогда справедливо P л Q о { X | F ( X) < ° } .

Верно и обратное. Пусть для оценки [ X] ( п ₄) выполняется условие F _Л ( X) <  °. Учитывая структуру формулы (4), такая ситуация возможна, если у «решающей» функции используется второе слагаемое, т.е. Г _Л ( X ) = в _p в q ( f_p + f Q ) / 2 , но это возможно, когда в _p =°, в Q = °, откуда следует, что p ( X) = 1, Q ( X) = 1. Аналогично доказываются и остальные случаи оценок интерпретаций переменных.

Для формул, использующих логическую связку «ИЛИ», можно сформулировать следующую теорему. Приведем её без доказательства.

Теорема 2 . Формула p v Q , связывающая предикаты, использующие базисные отношения, истинна тогда и только тогда и для тех оценок интерпретации переменных формулы, для которых «решающая» функция (5) меньше или равна нулю.

Замечание. Для решающей функции F _v ( X) следует использовать отношение порядка <, если хотя бы один из предикатов содержит это отношение.

Остальные логические связки можно выразить через логические операции «И», «ИЛИ», «НЕ». Таким образом, для произвольной формулы рекурсивно можно поставить в соответствие «решающую» F ф ( X) функцию, а следовательно, задачу проверки условия:

ф = ( F ф ( X) <  (или <) °).

3.    Алгоритм проверки истинности утверждений

Зададимся вопросом, что же нам даёт «решающая» функция? Применительно к задаче проверки истинности формул для случая, когда носителем интерпретации выступает конечное множество, алгоритм достаточно прост. Можно построить таблицу истинности формулы (на конечном множестве оценок) и этим закрыть проблему. В случае, когда носителем выступают действительные числа, задача значительно осложняется, поскольку число оценок становится бесконечным и область переменных формулы «раскрашивается» в чёрнобелые тона ( И или Л ). Кроме того, зная значение интерпретации формулы для какой-либо оценки (например, Л ), мы не можем знать, в каком направлении изменения переменных следует искать истинную оценку интерпретации переменных.

«Решающая» функция в пространстве переменных предиката устанавливает порядок (рис. 1), в связи с чем появляется возможность организации поиска таких сочетаний переменных F ( X ), для которых она принимает отрицательные значения. Для этого достаточно поставить задачу поиска глобального минимума «решающей» функции:

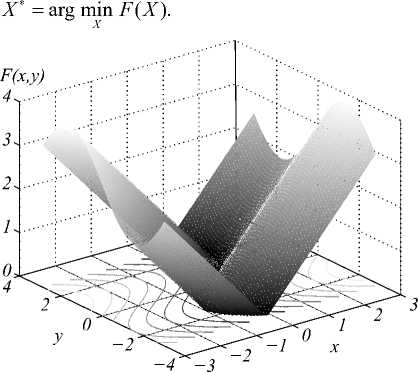
Рис. 1. Общий вид «решающей» функции

Для формулы φ, имеющей одно свободное вхождение переменной x, проверка её истинности эквивалентна оценке истинности формулы ∃ x Fφ (x), которая, в свою очередь, однозначно связана с проверкой условия переменных и вынесения кванторов в левую часть формулы [2]. При этом мы предполагаем, что в бескванторной части формулы используются только логические связки «И», «ИЛИ», «НЕ».

• 2.    Для бескванторной части формулы построим «решающую» функцию FM (X).

• 3.    Последовательно, шаг за шагом будем избавляться от связанных переменных в формуле (7), организовав рекурсивный процесс решения оптимизационных задач:

4.    Примеры

^ф n = K n x n M ( x X ,-, x n ),

_< ^ф n - 1 = K n - 1 x n - 1 ^ф n ( x l ,..., x n - 1 ),

ф = K 1 x 1 ^ф 2 ⁽ x 1 ).

Для каждой из задач (8) φ _n =K _i x_i φ _{i +1}( x ₁, ..., x_i ) строится «решающая» функция F φ _i ( x 1 , ..., x i ) и ищется её глобальный минимум. Причём если K _i = ∃ , то F _φ ( x ₁,..., x_{i - 1}) = min φ _{i + 1}( x ₁,..., x_i ) . В случае, если ⁱ                                     x_i

K _i = ∀ , то предварительно производится эквивалентное преобразование ∀ x φ = ∃ x φ и задача сводится к предыдущему случаю.

Алгоритм Тарского [3] позволяет установить истинность или ложность утверждений в элементарной теории действительных чисел с операциями сложения и умножения, т.е. для предикатов, использующих алгебраические функции. Рассмотрим, как работает наш алгоритм для предикатов, содержащих тригонометрические функции.

Пример 1. Проверка формулы ∀ x ∃ y (sin x = y ).

Прежде всего, преобразуем бескванторную часть формулы к нормализованному виду

M ( x . y ) = (sin x = y ) ≡ (sin x - y = 0) ≡

≡ (sin x - y <  0) ∧ (sin x - y ≤ 0) ≡

≡ ( y - sin x ≤ 0) ∧ (sin x - y ≤ 0).

Для (7) построим «решающую» функцию, положив θ = y – sin x и f = sin x – y , тогда в соответствии с (4) имеем

F _φ (arg min F _φ ( x ))) < 0 , x

т.е. решением задачи глобальной оптимизации (6) для соответствующей «решающей» функции.

Обобщая полученные результаты, несложно построить алгоритм проверки истинности утверждений о действительных числах в сигнатуре отношений порядка.

• 1.    Предварительно исходную замкнутую формулу необходимо привести к эквивалентной ей предварённой (пренексной) нормальной форме [2]:

где K i ∈{∀,∃} . Этого несложно добиться за счёт продвижения знака отрицания до атома, переименования

F M ( x , y ) = ( β θ θ+β f f )/( β θ +β f +β θ β f ) + +β θ β f ( θ+ f )/2.

На первом шаге свернём переменную y : φ ₁( x ) = ∃ y ( F_M ( x , y ) ≤ 0) ≡ (min F_M ( x , y ) ≤ 0).

y

Следующим шагом свернём переменную x :

φ= ∀ x (min F_M ( x , y ) ≤ 0) ≡ ∃ x (min F_M ( x , y ) ≤ 0) ≡

y

y

≡ ∃ x ( - min F_M ( x , y ) <  0) ≡ min(max F_M ( x , y )) <  0) ≡ xy

≡ min(max F_M ( x , y )) ≥ 0.

xy

В результате задача проверки истинности замкнутой формулы свелась к оптимизационной задаче и проверке условия

(min max F_M ( x , y ) ≥ 0) . xy

Вычислительные эксперименты показали, что при изменении переменной     x ∈ [–3; 3] функция

F1 (x) = max FM (x, y) ≡ 0 , следовательно, исходная y формула верна, по крайней мере, в рассматриваемом диапазоне изменения переменной x.

Пример 2 . Проверка невыполнимой формулы ∀ y ∃ x (sin x = y ).

Для данной формулы мы имеем аналогичную предыдущему случаю «решающую» функцию (9).

На первом шаге свернём переменную x :

φ ₁( y ) = ∃ x ( F_M ( x , y ) ≤ 0) ≡ (min F_M ( x , y ) ≤ 0) . x

Следующим шагом свернём переменную y :

φ= ∀ y (min F_M ( x , y ) ≤ 0) ≡ ∃ y (min F_M ( x , y ) ≤ 0) ≡ xx

≡ ∃ y ( - min F_M ( x , y ) <  0) ≡ min(max F_M ( x , y )) <  0) ≡ x        yx

≡ min (max F_M ( x , y )) ≥ 0. y _x

Для этого примера функция F ₁( y ) = max F_M ( x , y )

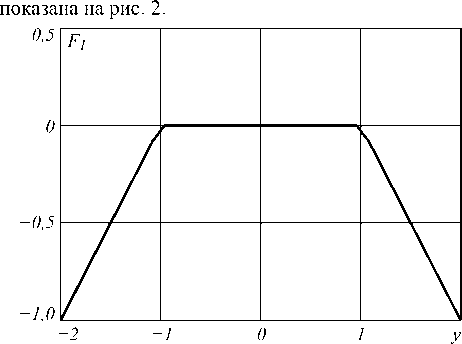
Рис. 2. График «решающей» функции F ₁( y )

Из рисунка видно, что min F1 (y) , по крайней ме-y ре, меньше –0,5, следовательно, исходная формула невыполнима.

Заключение

Кратко обсудим полученные результаты.

• 1.    Предложенный выше алгоритм, основанный на использовании «решающей» функции, позволил свести фактически переборную задачу проверки истинности любого утверждения о вещественных числах к оптимизационной задаче . Причём в новой версии алгоритма могут использоваться не только алгебраические, но и трансцендентные функции.

• 2.    Универсальный алгоритм Тарского оказался чрезвычайно неэффективным. Было доказано [3], что

• алгоритм Тарского будет работать дважды экспоненциальное время на некоторых «плохих» формулах в зависимости от их длины. Предлагаемый алгоритм, сводящийся к решению задачи глобальной оптимизации, в общем случае также имеет экспоненциальный характер роста его сложности [4], но уже в зависимости от числа оптимизируемых переменных. Размер формулы в этом случае не играет роли.

• 3.    Предложенный алгоритм имеет вариант практического использования, например, при проверке корректности графа управления сложного программного обеспечения (ПО), в той части, которая связана с проверкой логических выражений, управляющих вычислительным процессом. Такая задача актуальна в процессе тестирования и отладки ПО управления космическими объектами [5].

Кроме того, с точки зрения нахождения приближенного решения оптимизационные задачи имеют более стройные схемы их классификации, чем обычная теория NP -полноты. Дело в том, что практическая сложность реализации алгоритмов глобальной оптимизации во многом определяется свойствами оптимизируемой функции.

Например, для класса унимодальных гладких функций алгоритмы оптимизации сходятся к решению за полиномиальное время. В приведённом примере, использующем тригонометрическую функцию, как видно из рис. 1, «решающая» функция имеет множество равнозначных глобальных минимумов, расположенных на дне извилистого оврага. Очевидно, что нахождение любого из них не займёт много времени.

Более того, оптимизационные алгоритмы существенно снижают свою трудоёмкость (вплоть до полиномиального случая) при отказе от поиска точного решения. Известны многочисленные примеры приближённых алгоритмов оптимизации [6], решающих задачу оптимизации за полиномиальное время, к ним же относятся и рандомизированные алгоритмы. В нашем случае в задачах опровержения формулы (пример 2) достаточно найти любое, пусть даже приближённое решение меньше нуля.

Работа выполнена при государственной поддержке Министерства образования и науки РФ в рамках реализации мероприятия Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013–2020 годы.