Эффективный модуль упругости халькогенидных стекол (обзор)

Для кубических кристаллов квадрат среднеквадратичной скорости волн деформации v k ² является инвариантом суммы квадратов скоростей распространения продольных ( v l ) и поперечных ( v s ) акустических волн [1, 2]

vk

v + 2 vS

Это соотношение оказалось оправданным не только для кристаллов с другими решетками, но и для оксидных неорганических стекол [2, 3]. Произведение плотности ρ на квадрат среднеквадратичной скорости v k ² было названо усредненным модулем упругости [3]

K = ρν k ² (2)

Это название является не совсем удачным, поскольку известные упругие модули E , G и B также относятся к усредненным величинам. Поэтому предлагаем назвать K эффективным (или характерным) модулем упругости.

Настоящая работа посвящена исследованию природы величины K и установлению ее связи с упругими модулями и коэффициентом Пуассона применительно к бескислородным халькогенидным стеклам на примере стекол системы As-Tl-S, для которых известны необходимые экспериментальные данные об акустических и упругих свойствах [4] (табл. 1). Представляет интерес проверка применимости полученных ранее разработок [3] к халькогенидным стеклообразным твердым телам.

Поскольку эффективный модуль упругости оказывается связанным с параметром Грюнайзена и в свою очередь параметр Грюнайзена является однозначной функцией коэффициента Пуассона (см. далее), нами обсуждается проблема взаимосвязи линейных (гармонических) и нелинейных (ангармонических) характеристик твердых тел.

Эффективный модуль упругости, модуль объемного сжатия и коэффициент Пуассона

Из формулы модуля объемного сжатия B кубических кристаллов

С 11 + 2C

B а также из соотношения для произведения плотности и квадрата среднеквадратичной скорости звука vk2 [2]

Таблица 1

Плотность (ρ), скорости распространения продольных ( v l ) и поперечных ( v s ) акустических волн, упругие постоянные (μ, G , B ) [4] и рассчитанные из них параметр Грюнайзена (γ D ) и эффективный модуль упругости ( K )

для стекол составов x As 2 S 3 ∙(1- x )Tl 2 S

Состав стекла	Tl 2 S, мол. %	ρ∙10- 3 , кг/м3	v l , м/c	v s , м/с	μ	G ∙10- 8 Н/м2	B∙10- 8 Н/м2	γ D (12)	γ D (13)	K ∙10- 8 Н/м2
As 2 S 3	0	3,187	2650	1400	0,306	62	139	1,80	1,81	116
AsS 1.57 Tl 0.14	12,3	3,765	2680	1420	0,309	76	174	1,85	1,83	141
AsS 1.65 Tl 0.3	23,1	4,24	2580	1350	0,311	77	178	1,83	1,84	146
AsS 1.7 Tl 0.4	28,6	4,474	2550	1320	0,317	78	187	1,88	1,88	149
AsS 1.74 Tl 0.48	32,4	4,72	2510	1280	0,324	77	193	1,92	1,93	151
AsS 1.85 Tl 0.7	41,2	5,04	2440	1210	0,337	74	202	2,03	2,03	149
AsS 2 Tl	50	5,36	2320	1130	0,344	68	195	2,07	2,08	142

2_ С „ + 2 C 44 ^p k -    3

видно, что при выполнении условия Коши C 12 = C 44 , когда между однородно деформированными областями кубической решетки действуют центральные силы, величина K = ρ v k ² совпадает с модулем объемного сжатия K = B . Во всех других случаях произведение ρ v k ² отлично от B . Здесь C 11 , C 12 и C 44 — упругие постоянные 2-го порядка.

Убедимся, что так же, как и отношение модуля сдвига G к модулю объемного сжатия B [5],

G 3 ( 1 - 2 ц B 2 ^ 1 + ц

, величины G/K и B/K являются однозначными функциями коэффициента Пуассона μ.

Разделив G = ρ v s ² на K = ρ v k ² , получаем соотношение

G

K

v

v

s

² k

.

С помощью формулы (1) правую часть этого равенства выразим через квадраты продольной и поперечной скоростей звука

V,

-^ - 3 V^ + 2

v _k

л-1

I Vs    )

.

В теории упругости отношение ( v l ² / v s ² ) у изотропных тел является функцией коэффициента Пуассона [5]

V2 = 2 s

( 1

—

Ц )

11 - 2Ц )

.

Подставив (8) в выражение (7), а затем (7) в соотношение (6), приходим к заключению, что отношение G / K является функцией только коэффициента Пуассона

G - 3 Г 1-2ЦЛ

K 2 ( 2 - 3ц )

.

Из комбинации данной формулы с равенством (5) следует, что отношение B / K

также есть однозначная функция μ

B

K

1 + Ц 2 - 3ц

.

Этот результат был получен ранее иным способом [3] (с помощью более сложных выкладок с привлечением уравнений Леонтьева [2] и Беломестных– Теслевой [6], а также с использованием искусственного приема и некоторого ограничения).

Таким образом, во-первых, как и модуль сдвига, величина K = ρ v k ² выражается через произведение плотности на квадрат скорости звука и, во-вторых, при вы-

полнении условия Коши она совпадает с модулем объемного сжатия. В-третьих, так же, как и отношения упругих модулей, величины G/K и B/K являются однозначными функциями коэффициента Пуассона. Поэтому произведение ρ v k ² названо эффективным модулем упругости.

При установлении зависимости B / K от коэффициента Пуассона в виде (10) были использованы соотношения для изотропных кристаллов с кубическими решетками. Тем не менее, ранее было показано, что эта зависимость (10) применима к оксидным стеклам [3]. Рассмотрим применение выражения (10) к бескислородным халькогенидным стеклам мышьяк-сера-таллий.

Как видно из рис. 1, зависимость отношения B / K от функции коэффициента Пуассона (1+μ)/(2-3μ) является линейной, причем в соответствии с равенством (10) прямая проходит через начало координат с наклоном, равным единице, что подтверждает справедливость формулы (10) для рассматриваемых халькогенидных стекол. Необходимые экспериментальные данные взяты из работы [4] (табл. 1). Справедливость равенства (10) была установлена для силикатных стекол [3, 7]. Представляет интерес применимость зависимости (10) к другим оксидным неорганическим стеклам. Как видно из рис. 2, эта зависимость хорошо выполняется для метафосфатов щелочноземельных металлов (по данным [8], табл. 2).

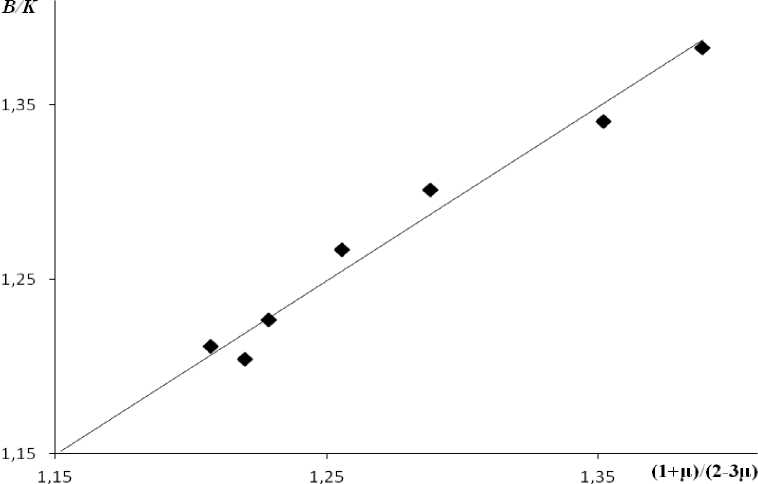
Рис. 1. Зависимость отношения модуля объемного сжатия к эффективному модулю упругости ( B / K ) от функции коэффициента Пуассона (1+ц)/(2-3ц) для халькогенидных стекол мышьяк-сера-таллий при различных содержаниях компонентов. Использованы данные работы [4]

Таблица 2

Физико-механические характеристики [8] и рассчитанные из них параметр Грюнайзена γ D и эффективный модуль упругости K для стеклообразных метафосфатов щелочноземельных металлов MeO — P 2 O 5 , где Me = Mg, Ca, Sr, Ba

Состав стекла по синтезу	ρ∙10-3, кг/м3	v l , м/с	v s , м/с	G ∙10-8, Н/м2	B ∙10-8, Н/м2	μ	γ D		K ∙10-8, Н/м2
							Фор-ла (12)	Фор-ла (13)
0.51MgO∙0.49P 2 O 5	2.475	5267	3110	239	367	0.233	1.42	1.42	388
0.50MgO∙0.50P 2 O 5	2.474	5264	3108	239	367	0.233	1.42	1.42	388
0.49MgO∙0.51P 2 O 5	2.477	5289	3121	241	371	0.233	1.42	1.42	392
0.51CaO∙0.49 P 2 O 5	2.604	5051	2858	213	381	0.264	1.57	1.57	363
0.50CaO∙0.50 P 2 O 5	2.618	5086	2869	216	390	0.267	1.58	1.59	369
0.49CaO∙0.51 P 2 O 5	2.604	5051	2857	213	381	0.265	1.57	1.57	363
0.51 SrO∙0.49 P 2 O 5	3.048	4603	2568	201	378	0.274	1.62	1.62	349
0.50 SrO∙0.50 P 2 O 5	3.030	4610	2577	201	376	0.273	1.62	1.62	349
0.49 SrO∙0.51 P 2 O 5	3.020	4612	2584	202	373	0.271	1.61	1.61	349
0.51BaO∙0.49P 2 O 5	3.411	4160	2269	176	356	0.288	1.70	1.70	314
0.50BaO∙0.50P 2 O 5	3.413	4178	2278	177	360	0.288	1.71	1.70	317
0.49BaO∙0.51P 2 O 5	3.385	4186	2291	177	356	0.286	1.69	1.69	316

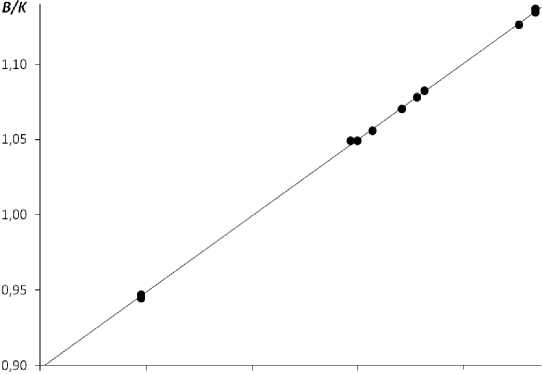
0,90            0,95            1,00            1,05           (I+JOX2"3!1)

Рис. 2. Линейная корреляция между B / K и (1+μ)/(2-3μ) для стеклообразных метафосфатов щелочноземельных металлов MeO–P 2 O 5 при различных содержаниях

MeO (Me = Mg, Ca, Sr, Ba). Использованы данные [8]

Эффективный модуль упругости и ангармонизм колебаний решетки

Одной из особенностей величины K = ρ v k ² является ее связь с параметром Грюнайзена γ D , который служит характеристикой нелинейности силы межатомного взаимодействия и ангармонизма колебаний решетки. Параметр Грюнайзена выражает изменение частоты нормальных колебаний решетки в зависимости от изменения объема системы и вычисляется по уравнению

_ PVB

CV

, где β — коэффициент объемного теплового расширения, CV и V — молярные теплоемкость и объем, B — изотермический модуль объемного сжатия. Наряду с уравнением Грюнайзена (11) для расчета γD используются другие соотношения. Заслуживают внимания, например, формулы Леонтьева [2]

3 f B

² 1 p v k

и Беломестных-Теслевой [6]

Y d ⁼H

1 + ^

2 — 3 ^

Примечательно то обстоятельство, что эти соотношения (12) и (13) находятся в согласии с уравнением Грюнайзена (11) для металлов, ионных и молекулярных кристаллов [3, 6]. Рис. 3 подтверждает согласие между уравнениями (12) и (13) применительно к рассматриваемым халькогенидным стеклам (табл. 1).

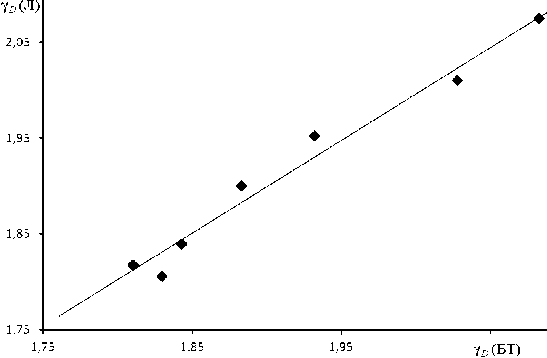
Рис. 3. Корреляция между значениями параметра Грюнайзена, рассчитанными по формулам Леонтьева γ D (Л) и Беломестных-Теслевой γ D (БТ), для халькогенидных стекол мышьяк-сера-таллий при различных содержаниях компонентов.

Использованы данные [4]

Из сравнения соотношения (10) с формулой Беломестных-Теслевой (13) следует взаимосвязь эффективного модуля упругости K и параметра Грюнайзена γ D

K = ³

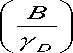
Обсуждение результатов

В работе [4] показано (табл. 1), что при увеличении содержания сульфида таллия Tl 2 S у стекол в системе As-S-Tl по сечению As 2 S–Tl 2 S наблюдается непрерывное возрастание коэффициента Пуассона от μ = 0.306 до μ = 0.344; соответственно, согласно формуле (13), так же непрерывно и монотонно возрастает и параметр Грюнайзена, от γ D = 1.8 до γ D = 2.1. Это указывает на ослабление каркаса стекол и разрыхление их структуры, что согласуется со снижением энергии активации вязкого течения [4]. Здесь наблюдается некоторая аналогия с щелоч-но-силикатными стеклами. Известно, что при росте содержания ионов щелочных металлов R ⁺ (содержания R 2 O, R= Li, Na, K) в щелочно-силикатных стеклах R 2 O-SiO 2 возрастает степень ионности межатомных связей и происходит переход от сетчатой структуры (у кварцевого стекла SiO 2 ) с направленными силами межатомного взаимодействия к преимущественно ионной разветвленной цепочечной структуре (у стекол R 2 O-SiO 2 ). Например, у натриево-силикатных стекол Na 2 O-SiO 2 при увеличении содержания окиси натрия Na 2 O (ионов Na ⁺ ) от 0 до 35 мол.% μ и γ D возрастают от μ = 0.17 и γ D = 1.2 до значений μ = 0.25 и γ D = 1.5 (табл. 3) [9], характерных для центральных сил взаимодействия ансамбля частиц. При этом у них убывает энергия активации вязкого течения.

Таблица 3

Параметр Грюнайзена и коэффициент Пуассона натриево-силикатных стекол Na 2 O-SiO 2 [9]

Состав стекол, мол.%		μ	γ D
SiO 2	Na 2 O
100	-	0.17	1.2
85	15	0.20	1.3
75	25	0.23	1.4
65	35	0.25	1.5

Формула Беломестных-Теслевой (13) однозначно связывает гармоническую (линейную) μ и ангармоническую (нелинейную) γ D характеристики. Встречаются другие подобные корреляции [10-12], например, известное эмпирическое правило Баркера [9], выражающее связь модуля упругости E с коэффициентом теплового расширения β: β ² Е ≡ const. Вместе с тем в настоящее время природа этого явления остается во многом неясной. Известны лишь попытки качественного приближенного объяснения данного факта [11-13].

В рамках одномерной модели твердого тела потенциальная энергия межатомного взаимодействия двух смежных атомов записывается в виде

ax2  bx3

U =

, где а = (d2U/dX2)r=ro — гармонический, b = -(1/2(

Л m + n + 3 ^

b =

2r ^ja

V roo   J и устанавливает функциональную зависимость в, E и подобных свойств от коэффициентов а и b. Отсюда объясняет обсуждаемое явление наличием связи между а и b типа (15) и зависимостью от них линейных и нелинейных величин.

Таким образом, подход Т.А. Конторовой указывает на принципиальную возможность реализации корреляции между, казалось бы, совершенно различными по своей природе физическими свойствами, в том числе между гармоническими и анграмоническими характеристиками твердых тел. Представляет интерес теория Пинеда [12], в рамках которой интерпретируются согласованные изменения коэффициента Пуассона р и параметра Грюнайзена уd в опытах по структурной релаксации и всестороннему сжатию металлических стекол.

Тем не менее продолжает оставаться не совсем ясным существо природы однозначной связи параметра линейной теории упругости μ с мерой нелинейности силы межатомного взаимодействия уd.

Среди работ, посвященных природе коэффициента Пуассона (коэффициента поперечной деформации, как иногда называют), заслуживает внимания подход Берлина, Ротенбурга и Басерста [14], где предложена модель случайно упакованных сфер, взаимодействующих друг с другом в месте контакта двумя видами сил: перпендикулярных к плоскости контакта (центральных сил) и тангенциальных (сил трения), действующих по касательной к данной плоскости. Предполагается, что нормальные f и тангенциальные ft силы пропорциональны соответ- ствующим смещениям xn и xt fn = апХп, ft =axt, где an и at — нормальная и тангенциальная жесткости. Из модели следует, что коэффициент Пуассона определяется отношением этих (сдвиговых и изгибных) жесткостей X = atI an [14]

1 - A и =----

4 + A

При X = 0 (an >> at) имеем p = 0.25, что соответствует ансамблю частиц с центральными силами. С ростом X величина р уменьшается и при X = 1 р = 0. Интересно отметить, что формула (16) предсказывает нижний предел коэффициента Пуассона р = -1 при X ^ да (at>>an). В самом деле, по теории упругости, как показали Ландау и Лифшиц [5], величина μ может меняться в пределах: -1 < ц< 0.5

Поскольку тангенциальная жесткость at связана с силой трения (с диссипацией энергии деформирования), можно ожидать зависимость параметра X = aMn от нелинейных эффектов, в частности, от ангармонизма. В самом деле, такая зави- симость λ(γD) следует из соотношений (13) и (16)

Л _(1.5 - Yd )

Yd

Это означает, что в формуле (16) в неявном виде заложена зависимость коэф-

фициента Пуассона μ от ангармонизма, мерой которого служит параметр

Грюнайзена γD.

Ангармонизм колебаний решетки и нелинейность силы межатомного взаимо-

действия проявляются в пластической деформации стеклообразных твердых тел

[15, 16]), что вполне естественно. Предел текучести σy — напряжение, выше ко-

торого наблюдается пластичность стекла, — определяется отношением модуля упругости E к параметру Грюнайзена [16]

^У

f EL Yd

Обращает внимание аналогичное отношение (B/γD) в формуле для величины K (14). В процессе пластической деформации, например, стеклообразных полимеров, усиливается ангармонизм (растет γD) и снижаются потенциальные барьеры межмолекулярного происхождения в сравнении с недеформированным состоянием, которое характеризуется межмолекулярным взаимодействием, определяемым модулем упругости E [15, 16].

Из соотношений (14) и (18) с привлечением известной формулы для B следует, что у стеклообразных материалов одного типа, у которых μ ≈ const, предел текучести пропорционален эффективному модулю упругости K f 1 -2^S

^У = ^--3--J K                 (19)

По формулам (12)–(14) и (18) можно вычислять параметр Грюнайзена на основе данных только механических испытаний, тогда как по известному уравнению Грюнайзена (11) величина γD рассчитывается главным образом по данным о теплофизических характеристиках. Приведенные выше примеры могут оказаться полезными при анализе механических свойств стекол с учетом ангармонизма [15, 16].

Заключение

Рассмотрен эффективный модуль упругости K халькогенидных стекол системы мышьяк-сера-таллий. Установлено, что у исследованных стекол отношение модуля объемного сжатия к эффективному модулю упругости K является однозначной функцией коэффициента Пуассона. У стеклообразных твердых тел одного класса с одинаковыми (близкими) коэффициентами Пуассона предел текучести пропорционален эффективному модулю упругости. Особенностью величины K является его тесная связь с параметром Грюнайзена. В связи с однозначной зависимостью коэффициента Пуассона от параметра Грюнайзена поднимается вопрос о природе корреляции между гармоническими и ангармоническими величинами. На данном этапе приходится допускать зависимость коэффициента Пуассона от ангармонизма, что требует в дальнейшем детального обоснования.