Эффекты модуляции тока в комплексной плазме тлеющего разряда с упорядоченными структурами

В исследованиях комплексной низкотемпературной плазмы (КНТП) принято разделять диагностические подходы по использованию возмущающих воздействий. Такое разделение объясняется целями и задачами исследования: если невозмущающая диагностика дает информацию о поведении объекта в отсутствии внешних воздействий в его естественном состоянии, то возмущающие методы отслеживают реакции на внешние воздействия не только с точки зрения изучения структуры и поведения самого объекта, но зачастую и с точки зрения изучения возможности управления объектом, например, для задач плазмохимии или при обработке твердофазных частиц в плазме (подробнее см.: [4], [5], [6]).

Основную часть работ, опубликованных в области возмущающей диагностики плазмы, составляют работы, относящиеся к высокочастотному разряду, при этом в них параметрические воздействия на плазму тлеющего разряда постоянного тока изучены недостаточно. Тем не менее уже было обнаружено модулирующее воздействие кратковременных импульсов адиабатического магнитного поля на кристалл в тлеющем разряде, вызывающее его смещение и затухающие пылезвуковые волны [7]; также были изучены эффекты воздействия на кристалл и окружающую его плазму пучков заряженных частиц различной энергии [2]. Газодинамические воздействия, использование направленного лазерного излучения и воздействия градиентом температур в тлеющем разряде описаны в [6], [11], [12].

Авторами вышеуказанных работ отмечается необходимость изучения новых методов параметрических воздействий на плазменно-пылевые структуры (ППС) с целью диагностики их параметров и управления такими их свойствами, как пространственное положение и форма структуры.

ПОСТАНОВКА ЭКСПЕРИМЕНТА

Предшествующие исследования КНТП показали существование ранее не известных эффектов в поведении частиц конденсированной дисперсной фазы (КДФ) в плазме тлеющего разряда постоянного тока, модулируемой гармоническими колебаниями малой амплитуды, подробно описанными в [3], [10]. Эти эффекты, не отмеченные ранее ни в одной из работ и очевидно обусловленные коллективными процессами в комплексной плазме, мотивировали нас приступить к исследованиям механизмов упомянутых явлений на основе их экспериментальных и теоретических исследований. Для проведения исследований была создана установка, позволяющая индуктивно накладывать синусоидальное напряжение в катодную (низковольтную) ветвь цепи питания разряда.

Для задания сигналов различной формы использовались генераторы частот Г3-109 и Г3-112 с одновременным контролем формы и амплитуды задаваемого сигнала на выходах сопрягающего устройства и после прохождения через разряд на осциллографе через гальваническую развязку (более подробно см.: [3], [10]). Амплитуда задаваемого возмущения менялась от 0,05 до 6 В при частотах сигнала от 10 Гц до 100 кГц, к этой же области частот принадлежат частоты предполагаемых пылезвуковых и ионных плазменных колебаний [1], [5], что и явилось основой для выбора диапазона возмущающих частот.

Для исследований в качестве рабочего газа был взят молекулярный азот при давлениях 0,2-0,6 мм рт. ст., падение напряжения на разряде составляло 450-1200 В, ток разряда - 0,51,4 мА (условия подбирались для получения максимально стабильных (0,4 и 0,6 мм рт. ст.) и нестабильных структур (0,2 мм рт. ст.)). В качестве кристаллообразующей пыли использовались полидисперсные порошки Al2O3 и Zn с равномерным разбросом размеров фракции - 520 мкм. Для образования кристалла производилось в среднем 3 инжекции пыли в разряд, среднее количество частиц, инжектируемое за 1 раз, - в пределах 100. Регистрация изображений пылинок кристалла в лазерном ноже производилась скоростной CCD-камерой, подключенной к персональному компьютеру. По масштабированным изображениям структур вычислялась высота кристалла, ширина, расстояние от нижней границы структуры до сужающего конуса. Затем по полученным кадрам при помощи специализированного ПО вычислялись средние межчастичные расстояния в структуре.

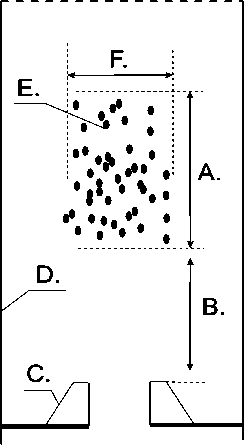
Рис. 1. Схема измерений:

A - вертикальный размер пылевой структуры, B - расстояние от нижней границы структуры до сужающего конуса, C - сужающий конус, D - стенка разрядной трубки, E - пылевая структура, F - горизонтальный размер пылевой структуры

Еще раз остановимся на том, что в исследовании регистрировались такие параметры, как пространственное положение элементов КДФ (в том числе их наличие / отсутствие), их вертикальное перемещение за время воздействия воз- мущающим сигналом, размер пылевой структуры по вертикали и горизонтали и динамика изменения структур во времени (за временные промежутки от 0,04 до 5 мин.). Для расчетов принимались данные, усредненные минимум по трем измерениям.

Наблюдения проводились при последовательной смене давлений рабочего газа от 0,2 до 0,6 мм рт. ст. c шагом 0,1 мм рт. ст., при каждом заданном давлении задавалось три различных значения тока (0,7, 1,0, 1,3 мА) с соответствую -щими значениями падения напряжения на разряде, при каждом из значений разрядного тока проводились замеры наблюдаемых параметров при частотах возмущающего сигнала от 10 до 200 Гц с шагом 10 Гц, 200-1000 Гц с шагом 100 Гц и далее на частотах 1, 5, 10, 15, 20, 40, 60, 80, 100 кГц.

При фиксированной частоте возмущения амплитуда возмущающего сигнала повышалась до уровня, при котором начиналось разрушение кристалла, или до уровня, при котором кристалл смещался за границу области регистрации. Каждый эксперимент повторялся трижды с усреднением результатов и вычислением доверительного интервала погрешности.

Таким образом, в ходе обработки данных анализировались зависимости наблюдаемых параметров от амплитуды и частоты задаваемого возмущения при разных газах, материалах и размерах фракции используемых частиц, различных начальных значениях, токах разряда и давлениях.

РЕЗУЛЬТАТЫ

При работе с синусоидальным возмущаю -щим сигналом, задаваемым извне, при амплитудных значениях сигнала, проходящего через разряд, порядка 1 % от падения напряжения на разряде наблюдались существенные (до нескольких раз) изменения размеров, формы кристалла и его положения в пространстве разряда.

Минимальная амплитуда вводимого возмущения, при которой было зарегистрировано воздействие на кристалл, зафиксирована при давлении 0,2 мм рт. ст., падении напряжения на разряде 550 В и составила 0,01 В. За минимальное воздействие было принято такое воздействие, при котором наблюдаемый параметр (например, смещение частиц пылевой структуры или амплитуда колебаний отдельных частиц) как минимум втрое превышал средние значения флуктуаций наблюдаемых параметров.

Было определено, что с ростом давления газа и падением напряжения на разряде минимальная возмущающая амплитуда растет нелинейно. Максимальное ее значение (6 В) было зафиксировано в молекулярном азоте при давлении 0,6 мм рт. ст. и падении напряжения 1300 В при токе 1,4 мА. Необходимо отметить, что максимальное значение амплитуды вводимого возму- щения намеренно ограничивалось в первую очередь целью эксперимента - изучить влияние малых возмущений, и во вторую - техническими возможностями. Таким образом, максимальное амплитудное значение вводимого возмущения может достигать и больших величин.

Среди зарегистрированных эффектов есть требующие дополнительного изучения и описания. Так, при частотах 1-40 кГц при наращивании амплитуды внешнего возмущения наблюдалось смещение кристалла вниз, сопровождающееся «растяжением» самого кристалла и «разряжением» его структуры по вертикали (рис. 2) без сужения (в рамках погрешности измерения) в горизонтальной плоскости.

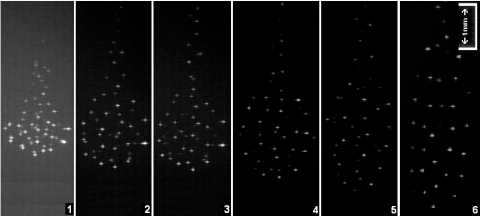
Рис. 2. Кристалл в N 2 при 0,4 мм рт. ст., токе 0,9 мА, напряжении на разряде 950 В, синусоидальная модуляция - 15 кГц, амплитуда: 1 - 0,1 В, 2 - 0,2 В, 3 - 0,4 В, 4 - 0,6 В, 5 - 0,8 В, 6 - 1,0 В

Последнее явление вызывает особый интерес, поэтому рассмотрим эффект более тщательно. Подробные наблюдения показали, что структуры, состоящие из малого количества (10-20) частиц, более устойчивы к вводимым возмущениям и показывают крутую зависимость увеличения размеров от амплитуд вводимых сигналов (до 4 раз), без разрушения. Максимальное изменение вертикальных размеров кристалла при заданной амплитуде возмущения зарегистрировано в области 15-20 кГц вне зависимости от давления рабочего газа.

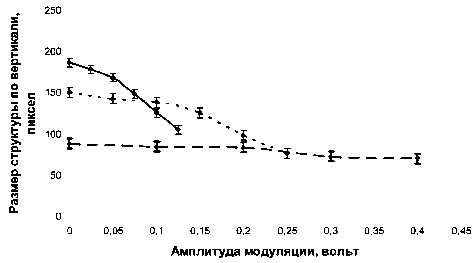
Рис. 3. N 2 , изменение вертикальных размеров кристалла, синусоидальная модуляция - 60 кГц, амплитуда - 0-0,4 В, в 1 мм 70 пикс., сплошная линия - ток 1 мА, падение напряжения -1,3 кВ, пунктир - ток 1,3 мА, падение напряжения - 1,3 кВ, мелкий пунктир - ток 0,7 мА, падение напряжения - 1,3 кВ

С ростом частоты возмущения эффект растяжения кристалла постепенно уменьшается, практически исчезая к 30-47,5 кГц (зависит от давле ния газа), сменяясь эффектом сжатия кристалла с «уплотнением» его структуры по вертикали.

При постепенном наращивании амплитуды модуляции кристалл достигает максимального сжатия, после чего уплотнение прекращается при амплитудах сигнала, регистрируемого после прохождения через разряд, порядка 6 В (зависит от типа газа, давления и падения напряжения на разряде). Наблюдаемое сжатие прямо пропорционально исходным размерам кристалла.

АНАЛИЗ РЕЗУЛЬТАТОВ И ВЫВОДЫ

Для дальнейшего анализа нам необходимо выявить действительно значимые факторы, влияющие на поведение ППС, и определить вид зависимостей параметров структур от этих факторов. Введем следующие обозначения: d - линейный размер структуры по горизонтали (рис. 1F), L - линейный размер структуры по вертикали (рис. 1A), k - коэффициент, определяющий скорость изменения линейных размеров плазменно-пылевой структуры, V - амплитуда возмущающего напряжения, v - частота возмущающего воздействия, I - ток разряда. Известно, что давление газа и напряжение на разряде связаны с током разряда и начальным размером ППС, поэтому указанные величины в расчет не принимались.

Напомним, что после напуска газа и зажигания разряда, формирования ППС производилась регистрация линейных размеров ППС, далее с помощью генератора колебаний в разряд вводилось возмущающее воздействие в виде тока переменной частоты v амплитудой колебаний V, вследствие чего линейные размеры ППС (рис. 1) изменялись и снова регистрировались. Эксперименты проводились при различных параметрах разряда - ток (I) и давление рабочего газа (Р).

Диапазоны изменения параметров: V [0^6,2] В, v [10^100000] Гц, I [0,7...1,3] мА, таким образом, при установке значений I и v с малым шагом варьировалась величина V.

В ходе обработки данных были поставлены следующие задачи.

• 1.    Проверка гипотезы о наличии зависимостей линейных размеров ППС от величин возмущающих параметров (V [В], v [Гц]) и параметра разряда (I [А]) с использованием корреляционного анализа.

• 2.    Проверка гипотезы о влиянии возмущающих параметров (V [В], v [Гц]) и параметра разряда (I [А]) на линейные размеры ППС и по возможности оценка степени влияния с использованием дисперсионного анализа.

• 3.    Определение зависимости между линейными размерами ППС и величинами возмущающих параметров (V[B], v [Гц]) и параметра разряда (I [А]) в случае принятия гипотезы (п. 1) и выражение в виде функции L = f(V, v , I).

Введем дополнительный параметр k, который будет характеризовать скорость изменения размеров структуры от изменения параметров: в данном случае мы имеем «мгновенное изменение» параметра k, для его вычисления для группы измерений при фиксированных Р, I и v необходимо построить графики зависимостей d(V) и L(V) (рис. 4).

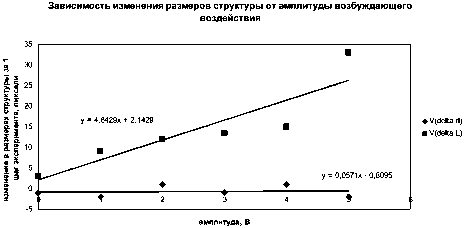
Рис. 4. Экспериментальные данные и коэффициент скорости изменения размеров

После этого, аппроксимировав точки прямой (в обработке мы намеренно упрощаем используемые модели с целью выявления имеющихся зависимостей: далее выявленные зависимости будут обработаны более тщательно), мы можем найти коэффициент k, характеризующий скорость изменения линейных размеров структуры при фиксированных Р, I и v . Иными словами, k = tg( a ) или k - это коэффициент в выражении у = kx + b.

Построив подобные графики для всех экспериментов, можно получить таблицу с данными и характеризующие ее графики зависимостей k_L( v ) и ky( v ), отражающие изменение скорости колебаний размеров ППС в двух направлениях (L и d).

Зависимость скорости изменения размера структуры от частоты возбуходающего напряжения в вертикальной плоскости при различных

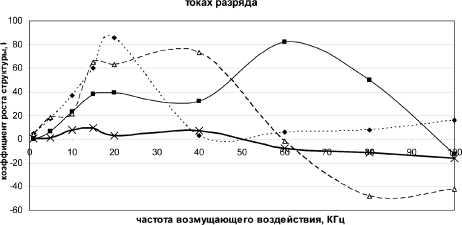
■♦■■■0,8 А       --■--0,7 А       --Д--1А       --И--1,3 А

Рис. 5. Скорость изменения вертикального размера структуры

На рис. 5 показано, что при различных токах картина изменений скоростей (для направления L) выглядит по-разному, при этом можно четко выделить 2 пика в областях: [15...20] Гц и > 40 Гц, которые показывают, что при определенных частотах возбуждающего воздействия, возможно, наблюдаются эффекты коллективного воздействия на ППС или же явления резонансной частоты, когда совокупность факторов усиливает возбуждающее воздействие. Также видно, что при высоких токах разряда влияние на структуру меньше, чем при малых.

Зависимость же скорости изменения размера структуры по горизонтали носит сложный характер, возможно, имеющий флуктуационную природу. Этот вывод можно сделать из предпо-ложения, что из-за сил электростатического отталкивания при уменьшении размера структуры из заряженных частиц в одной плоскости она должна увеличиваться в размерах в другой плоскости, и наоборот, чего не наблюдается.

Также был проведен анализ изменения размеров структуры в пределах одного эксперимента: исходя из вышеизложенного можно опреде -лить только скорость изменения линейных размеров структуры, но в то же время важной является информация о том, как изменялись эти размеры - сжималась ППС или расширялась.

Эти данные необходимы для адекватного построения аналитического вида зависимости на различных интервалах частоты ( v ). Для определения того, насколько изменились размеры ППС за один эксперимент для каждого эксперимента, введем параметр z, который будет равняться разности межу размером структуры в начале эксперимента и в конце.

Построим графики зависимостей z_L( v ) и z_d( v ) при различных токах.

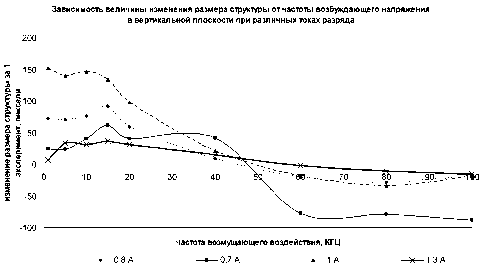
Рис. 6. Изменение вертикального размера структуры за 1 эксперимент

Из графика на рис. 6 видно, что ППС перестает растягиваться в вертикальном направлении при частотах возмущения от 40 до 60 кГц. Точки пересечения кривых с осью размеров структуры совпадают со значениями, подобранными экспе-риментально, - частотами, при которых вертикальный размер структуры не изменяется.

При этом в горизонтальном направлении не наблюдается картины, аналогичной вертикальному. Как было отмечено выше, при изменении одного из линейных параметров ППС, например L, должна меняться и d, то есть при сжатии ППС по вертикали она должна расширяться по горизонтали. Но на основании второго графика мы видим, что при росте длины кристалла (L) его толщина флуктуирует при возмущениях с часто -тами, лежащими в промежутке от 1 до 50 кГц, а некоторые зависимости можно проследить лишь после возмущений частотами выше 50 кГц.

Для проверки гипотезы о том, что зависимостей между линейными размерами ППС от величин возмущающих параметров (V, v ) и параметров разряда (I) не существует, был использован корреляционный анализ.

Проанализировав наличие / отсутствие зависимостей и опуская расчеты, можно сделать следующие выводы.

• 1.    Гипотеза об отсутствии зависимости между линейными размерами ППС по горизонтали (d) от амплитуды проверена по t-критерию на уровне значимости 5 % и для интервала v = [1...40] кГц принята, а для интервала v = [60...100] кГц отвергнута.

• 2.    Гипотеза об отсутствии зависимости между линейными размерами ППС по вертикали (L) от амплитуды проверена по t-критерию на уровне значимости 5 % и отвергнута на всем интервале.

• 3.    Гипотезу о зависимости между линейными размерами ППС (d и L) от частоты и силы тока исходя из полученных данных проверить нельзя, так как исходные размеры структур различны. Изменение размера структуры в ходе эксперимента зависит от изначальных размеров ППС, то есть определить зависимость между изменением размеров ППС, частотой и током не представляется возможным, так как при проведении эксперимента с другой частотой / током ППС формировалась заново.

• 4.    Для проверки гипотезы о том, что возмущающие параметры ( v ) и параметры разряда (I) не влияют на изменение линейных размеров ППС, воспользуемся дисперсионным анализом и, опустив расчеты, отметим, что гипотеза о влиянии частоты возмущения ( v ) на изменение вертикальных линейных размеров ППС (L) проверена по F-критерию на уровне значимости 5 % и принята.

• 5.    Гипотеза о влиянии тока разряда (I) на изменение вертикальных линейных размеров ППС (L) проверена по F-критерию на уровне значимости 5 % и отвергнута.

• 6.    Повторив расчеты для горизонтальных размеров, выясним, что гипотеза о влиянии частоты возмущения на изменение горизонтальных линейных размеров ППС (d) проверена по F-критерию на уровне значимости 5 % и принята.

• 7.    Аналогично гипотеза о влиянии тока разряда (I) на изменение горизонтальных линейных размеров ППС (d) проверена по F-критерию на уровне значимости 5 % и отвергнута.

При этом можно оценить, как изменялись линейные размеры ППС, используя данные о том, насколько выросла / уменьшилась структура при различных параметрах (I, V, v ). Оценив наличие зависимости между I, v и z - коэффициентом, показывающим, как изменились линейные размеры структуры за один эксперимент, и рассчитав коэффициенты корреляции для направления d и L, можно сказать: гипотеза об отсутствии зависимости между изменением линейных размеров ППС (L) от частоты проверена по t-критерию на уровне значимости 5 % и отвергнута; гипотеза об отсутствии зависимости между изменением линейных размеров ППС (d) от частоты проверена по t-критерию на уровне значимости 5 % и принята.

Влияния тока разряда на изменение размеров структур либо нет, либо оно незначительно относительно остальных факторов.

После выявления влияющих факторов необходимо определить зависимость между линейными размерами ППС и величинами возмущающих параметров (V, v ) и параметрами разряда (I), в случае принятия гипотезы об их влиянии и выразить в виде функции L = f(V, v , I).

Ранее было показано отсутствие влияния тока на размеры структуры и флуктуационный характер изменений размера ППС в направлении d. Таким образом, представляется возможным построить зависимость между размерами в направлении L от частоты ( v ) и амплитуды (V)

Модель аналитической зависимости:

• 3,6                  3,6

• L I = £ A i * V + £ B_i* V + C .          (1)

i =- 3, j = 1             i =- 3, j = 1

Для подбора параметров A 1 6 , B 1 6 и C воспользуемся методом наименьших квадратов и методами оптимизации целевых функций.

Целевая функция:

• ^W = £ ⁽ практ - ^Lmeop ) ^ ⁰ .                    ⁽²⁾

Использованные методы: «Поиск решения», метод случайных выбросов, метод Хука -Дживса.

Полученные модели зависимостей:

L I =₀₈ = 3,14 V ³ - 0,000 v ³ - 33 V 2 3 + 0,11 v ² +

• + 116,7V- 11,24v + 6,571 - 0,444 -

• VV

  • - 12441 + 690,46 4 + 406. vv

Адекватность модели для тока I = 0,8 мА: модель адекватна на уровне 10 %.

• L I = ₀,₇ = 2,49 V ³ - 25,81 V ² + 83,46 V - 0,18 v + 3,52 1 -

  • - 0,07   - 25,6981 + 182,614 +139,50.

• .      V 2       V       V \.

Адекватность модели для тока I = 0,7 мА: модель адекватна на уровне 10 %.

L I = 1 = 0,39 V ³ - 9,66 V ² + 79,38 V - 0,16 v ² - 10,54 v +

111   1

+ 2,23 0,17    - 1209 - + 865,63 -у + 339,51.

V V ² v ’ v'

Адекватность модели для тока I = 1 мА: модель адекватна на уровне 10 %.

L,= 13 = 0,88 V ³ + 0,0004 v ³ - 11,09 V ² + 42,60 V -

• ,                     1              11

• -0,07v2 -3,2v +1,19 0,02 — -123,56- +

V V2         v

+89,544 + 115,21.

v

Адекватность модели для тока І = 1,3 мА: модель адекватна на уровне 10 %.

ПРОВЕРКА РЕЗУЛЬТАТОВ

Адекватность моделей на уровне 10 % объясняется введением в расчеты данных для различных начальных размеров ППС и при раздельной обработке экспериментальных данных, например, по начальным размерам ППС и выделении двух интервалов частот возмущений (для сжатия структур и их растяжения) возможно построение моделей, адекватных на уровне не менее 5 %.

Тем не менее подстановка новых экспериментальных данных в модели 6‒9 дает среднее расхождение 6 и 9 пикселей при размере структуры соответственно 150 и 210 пикселей, полностью входя в доверительный интервал и позволяя говорить об адекватности полученных зависимостей.

ЗАКЛЮЧЕНИЕ

Описан новый метод воздействия на комплексную низкотемпературную плазму путем наложения гармонического сигнала на разрядный ток тлеющего разряда. Исследовано влияние слабых (порядка 1 % от падения напряжения на разряде) гармонических сигналов частоты 10‒100000 Гц на электростатическое поле плазмы положительного столба тлеющего разряда с упорядоченными структурами.

Обнаружены и описаны эффекты изменения вертикальных размеров кристалла, его положения в пространстве разряда в зависимости от амплитуды и частоты возмущающего сигнала, механизмы которых подлежат определению. Зафиксированы вынужденные колебания частиц разряда и стабилизация пылевых структур, совершающих самостоятельные колебания, определяемые модуляцией электрического поля разряда, схожие с колебаниями, ранее зарегистрированными в ВЧ-разряде [1].

Обнаружена возможность плавно менять положение кристалла в разряде по высоте и изменять форму кристалла путем изменения амплитудного значения возмущающего сигнала.

Для наблюдавшихся эффектов построены графики, отражающие характер зависимостей от частот и амплитуд вводимых возмущений на частотах 1, 5, 10, 15, 20, 40, 60, 80, 100 кГц, при давлениях газа (Ν2) 0,2, 0,4, 0,6 мм рт. ст. и падениях напряжения 700, 1000 и 1300 В.

Полученные данные были обработаны с целью выявления влияющих параметров, после чего были построены аналитические зависимости, отражающие зависимость линейных размеров ППС от параметров вводимого возмущения. Модели проверены и являются достаточно адекватными для того, чтобы с их помощью осуществлять целевое управление параметрами ППС в тлеющем разряде соответствующих условий.