Эффекты прерывистой неупругости при распространении сейсмической волны в зоне малых скоростей

Изучение физических механизмов распространения и затухания сейсмических волн, несмотря на свою давнюю историю, до сих пор является актуальной задачей. Для решения этой задачи современный подход использует новые знания о деформации горных пород, полученные на микромасштабном уровне. Классическая вязкоупругая модель хорошо описывает дисперсию и релаксацию [5, 23]. Однако эта модель не объясняет механизм, например, неоднозначности амплитудной зависимости скорости волны и затухания. Этот наводит на мысль о существовании какого-то не учитываемого механизма неупругости.

Изучение динамических характеристик пород достаточно полно описано в работе [2]. Данные получены при больших и умеренных деформациях, однако здесь не рассматриваются амплитудные и другие нетипичные эффекты. Изучение нелинейных эффектов в сейсмике показало возможность их действия даже при малых деформациях [4, 8]. Эти работы дали толчок к дальнейшему изучению и поиску физических причин этих эффектов.

Обзор по амплитудной зависимости скоростей волн и затухания [26] представляет эксперименты, выполненные на образцах пород при гармонических колебаниях, и теоретические положения. Большинство данных указывает на уменьшение скорости волны и увеличение затухания при увеличении амплитуды [23; 31, 34]. Немногочисленные данные для пород показывают, наоборот, увели-

чение скорости волны и уменьшение затухания волны при увеличении амплитуды [20; 37]. Возможность нестандартного поведения скоростей волн была обоснована в теоретических работах [24; 20; 18]. Здесь показано, что уменьшение или увеличение модуля упругости происходит в соответствии с положительным или отрицательным характером кривизны диаграммы о(е) .

Имеются немногочисленные полевые эксперименты по амплитудной зависимости скоростей волн, которые проведены в подпочвенном слое в неглубоких ямках или на берегу водоема [37]. Записи показывают, что с увеличением амплитуды сигнала скорость волны может как увеличиваться, так и уменьшаться. Имеет место также остаточный гистерезис скоростей волн, что свидетельствует о необратимых деформациях, вызванных сейсмической волной. Необычные данные по амплитудной зависимости получены также в лабораторных экспериментах [7]. Установлено, что в сухом и водонасыщенном песчанике в ультразвуковом диапазоне частот параметр затухания является более чувствительным к вариации амплитуды, чем скорость волны.

Данные указывают, что нестандартные эффекты обусловлены дефектностью пород, микро-неоднородностью, наличием тонких пленок, микротрещин, сложностью фазового состава. Эксперименты с использованием современной аппаратуры для регистрации волнового процесса и электронной микроскопии это подтверждают [19]. Например, данные

MINING SCIENCE AND TECHNOLOGY для кристаллического оливина показывают влияние нанометровых межзеренных соединений на параметр затухания поперечной волны. Эти межзерновые контакты имеют аномальные значения модуля упругости и вызывают необычные трансформации параметра затухания Q-1(го). Некоторые теоретические подходы и экспериментальные работы также выполнены в этом направлении [35; 11; 36].

Целью статьи является установление проявлений скачкообразной прерывистой не-упругости в породах, вызванных сейсмической волной, и сопоставление этих данных с результатами квазистатических экспериментов и других новейших исследований.

Методика и техника эксперимента

Эксперименты проводились на Быст-ровском полигоне в Новосибирской области. Верхняя часть разреза (ЗМС) является относительно однородной (отсутствуют отражающие границы) и сложена из суглинков мощностью несколько десятков метров. Суглинки состоят из песка, ила и глины в концентрации около 40 - 15 - 45 %, соответственно. Размер глинистых частиц и песчаных зерен составляет от пяти до десятков микрометров. Суглинки до глубины ~3 м относительно сухие, до ~8,5 м - частично водонасыщенные, а далее полностью водонасыщенные. Скорость продольной волны в сухих и частично насыщенных суглинках составляет V p = 240-500 м/с, а в полностью насыщенных - V p ~ 1500 м/с.

Источник излучения располагался в шурфе глубиной около 1 м. Вблизи источника на расстоянии 0,4-1 м располагался первый приемник сигналов. Второй приемник размещался в скважине на глубине 1 м и на расстоянии от источника 6 или 14 м. Источник состоит из набора пьезоэлектрических дисков. Преобладающая частота излучаемого импульса в ближнем приемнике ~1100-3300 Гц, а в дальнем приемнике ~120-340 Гц. Излучение осуществляется че-

рез упругую оболочку с жидкостью, контактирующую со стенкой скважины. Пьезоэлектрический приемник давления контактирует со стенкой скважины аналогичным образом, что обеспечивает хороший контакт со средой. Сейсмическая запись - это напряжение в функции времени, о( t ) , время квантования t _квант = 20 мкс и t _квант = 125 мкс. Шаг квантования амплитуды ( A квант ) в АЦП составляет 78 мВ. Амплитудные значения в вольтах были преобразованы в величины механического напряжения, используя коэффициент преобразования K _пр = 100 ц В/Па. Приемник сигналов имеет предусилитель с коэффициентом усиления K = 100. Сигналы в цифровой форме записывались на компьютер. Амплитуда входного сигнала изменялась дискретно от минимума до максимума: A 1 ^ A ₂ ^ A 3 ^ A ₄. Амплитуда возрастает как A ₂/ A 1 = 1,5; A ₃/ A 1 = 2,0; A ₄/ A 1 = 2,5. На расстоянии до 14 м от источника напряжение в среде составляет приблизительно единицы-десятки паскалей, а диапазон деформаций ~10^-8-10^-6. Это малые деформации, находящиеся ниже условного предела упругости.

Результаты и обсуждение

Анализ сейсмических записей проводился с использованием цифрового высокоразрешающего отображения сигнала в увеличенном масштабе. Отображение получено соединением всех точек квантования ( t _квант) цифровых амплитудных значений на трассе прямолинейными отрезками (без сглаживания). Такое представление сигнала позволяет детально рассмотреть динамический процесс, т.е. процесс развития напряжения (деформации) во времени. Иллюстрации приводятся как в аналоговом, так и цифровом отображении.

Результаты

На рис. 1 представлены шесть одновременно полученных записей сигналов в аналоговом виде, зарегистрированных на трех величинах амплитуды ( А 1 , А ₂, А 3 ). Из них три трассы - это записи первого (ближнего к ис-

MINING SCIENCE AND TECHNOLOGY точнику) приемника, установленного в скважине на глубине 1 м, и три трассы, записанные вторым приемником, находящимся в скважине на глубине 6 м в 1 м от источника.

Рассмотрение записей в цифровом отображении показывает следующее. Ввиду невозможности размещения всей записи на одном рисунке, она иллюстрируется отдельными частями. На рис. 2 показаны участки записей первого полупериода импульса, зарегистрированного вблизи источника а и импульса - на глубине 6 м (ниже источника) б . Сравнение записей а и б показывает их качественное различие. На всех амплитудах профиль первичного сигнала a_s ( t ) довольно гладкий. Профиль ^ ( t ) имеет осложнения в виде плато 1 различной протяженности, локального падения напряжения 2 (помечены пунктирным овалом) и участков резкого изменения крутизны фронта волны 3 (помечены стрелками). Здесь крутизна фронта в течение одного t квант изменяется в 9 раз. Перечисленные осложнения имеют здесь значительное распространение.

На рис. 3 показаны участки записей второго (положительного) полупериода ближнего импульса а и аналогичного дальнего полупериода б , зарегистрированного на глубине 6 м. Сравнение этих записей дает такой же результат, который был описан выше. Первая и повторная записи на одной и той же величине амплитуды А2, зарегистрированные дальним приемником, показаны на рис. 4. Эти импульсы в аналоговой форме представлены на рис. 4, а . Детальную картину в цифровом отображении можно видеть на трех интервалах записи, где участок б представляет запись первого минимума, участки в и г – это фрагменты восходящего и нисходящего фронта импульса соответственно. Здесь имеют место те же нестандартные проявления и наблюдаются те же самые нюансы между первой и повторной записями, которые описаны выше. Падение напряжения заменяется полочкой (в рис. 4 помечено стрелками в прямоугольнике). Имеются участки фронта импульса, которые свободны от нестандартных проявлений (рис. 4, г ).

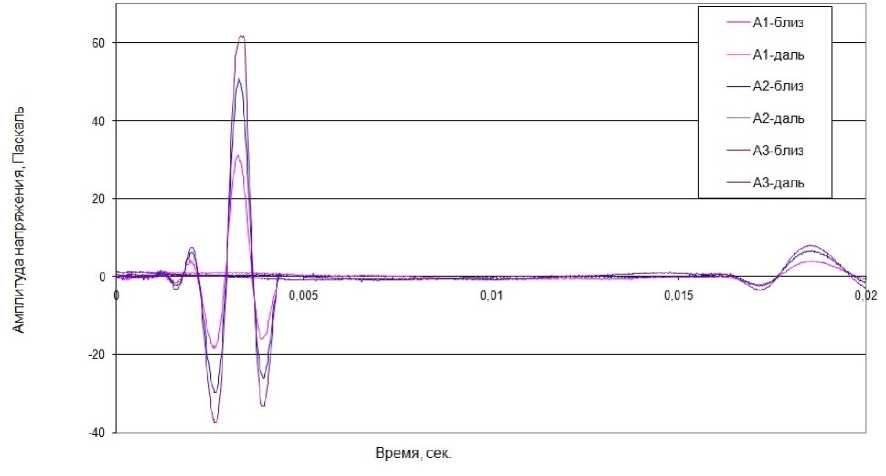
Рис. 1. Аналоговые записи сигналов на трех величинах амплитуды ( A 1 , A 2 . A 3 ), полученные вблизи от источника и на удалении от него

Fig. 1. Seismic response analog records at three values of amplitudes ( A ₁ , A ₂ , A ₃ ) obtained near the source (pulse emitter) and at a distance from it

MINING SCIENCE AND TECHNOLOGY

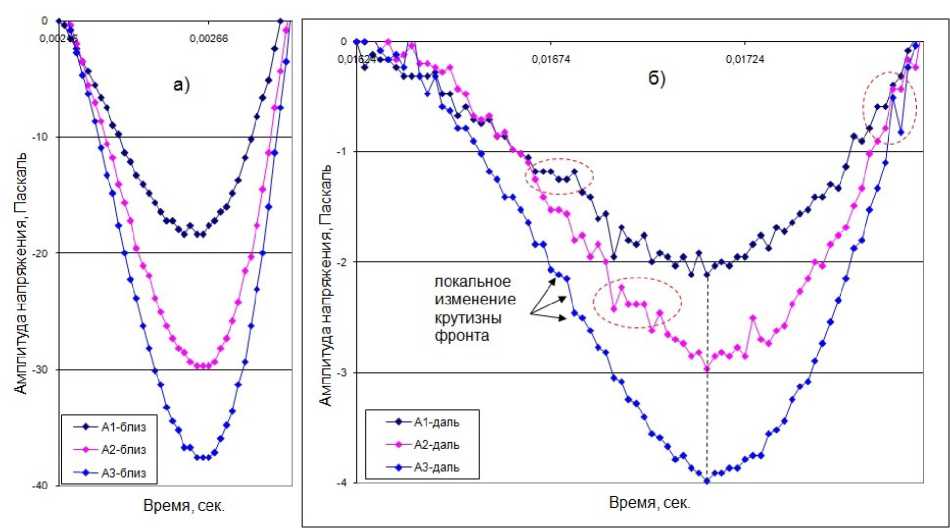
Рис. 2. Участки записей первого полупериода ближнего к источнику импульса ( а ) и импульса, зарегистрированного на глубине 6 м ( б )

Fig. 2. Sections of the records of the first semiperiod of the pulse closest to the source ( a ) and the pulse recorded at a depth of 6 m ( b )

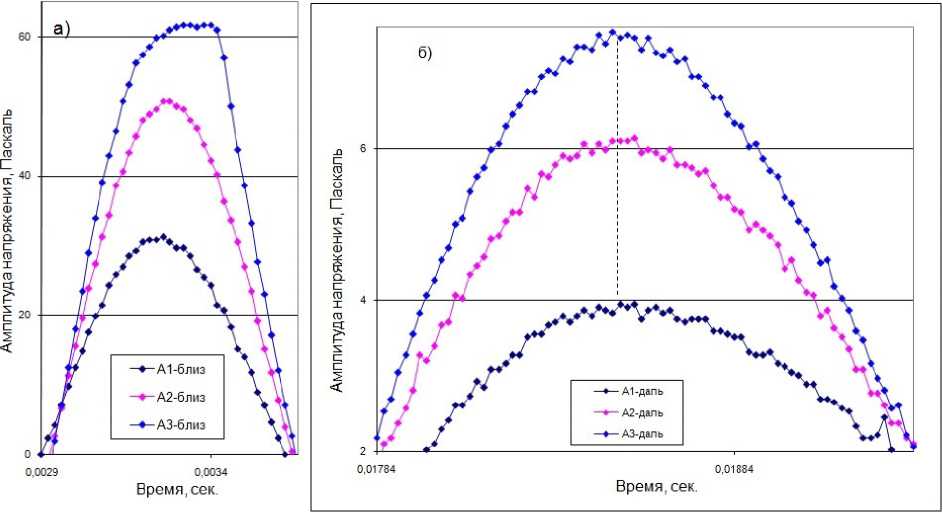
Рис. 3. Участки записей положительного полупериода ближнего импульса ( а ) и аналогового полупериода импульса, зарегистрированного на глубине 6 м ( б )

Fig. 3. Sections of the records of the positive semiperiod of the pulse closest to the source ( a ) and the analog semiperiod of the pulse recorded at a depth of 6 m ( b )

MINING SCIENCE AND TECHNOLOGY

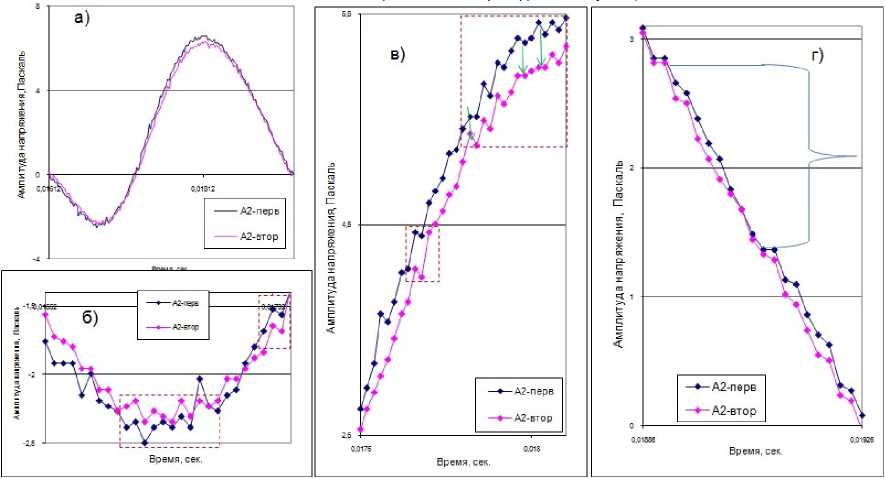
Рис. 4. Первая и повторная записи на одной и той же величине амплитуды (A 2 ),

зарегистрированные дальним приемником:

а – импульс в аналоговой форме; б – первый минимум; в , г – фрагменты восходящего и нисходящего фронтов импульса, соответственно

Fig. 4. The first and repeated records at the same amplitude (A ₂ ), recorded by the far receiver tool: a – the analog pulse record; b – the first minimum; c, d – fragments of the pulse ramp and downgoing front, respectively

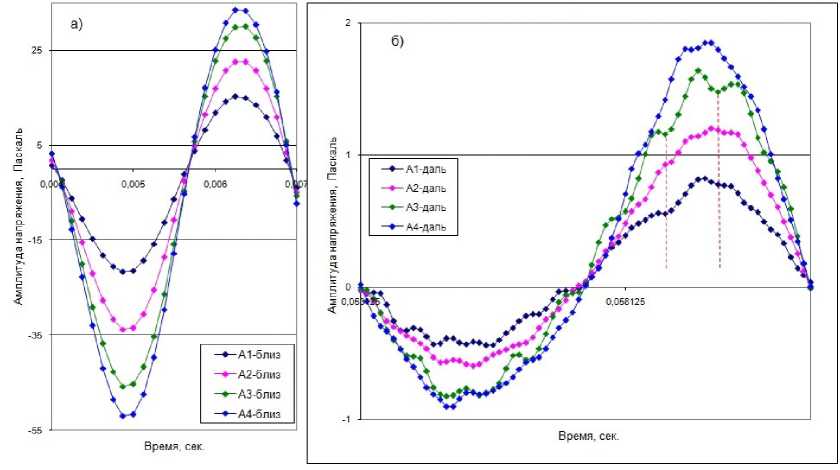
Рис. 5. Импульсы напряжения, зарегистрированные ближним к источнику приемником ( а ) и дальним приемником ( б ), расположенным в 1 м скважине на расстоянии 14 м от источника

Fig. 5. Stress pulses recorded by the receiver tool closest to the source ( a ) and the far receiver ( b ), located in 1-m borehole at a distance of 14 m from the source

На рис. 5 показаны записи ближнего приемника а и дальнего приемника б , расположенных на расстоянии 1 и 14 м от источника. Профиль волны вдали от источника на всех амплитудах осложнен плато и участками падения напряжения. Падающий фронт по-

ложительного полупериода почти не имеет осложнений. На рис. 6 показан пример записи импульса в 14 м от источника, где имеется наличие протяженного осложнения на восходящем фронте и его отсутствие на падающем фронте. В интервале времени ∆ t = t 2 - t 1 на

MINING SCIENCE AND TECHNOLOGY всех величинах амплитуды наблюдается уменьшение крутизны фронта, которое имеет структурированный характер. Здесь осложнения представлены в виде плато и падения напряжения пилообразной формы. Вне этого участка поведение профиля напряжения относительно монотонное. С увеличением величины амплитуды размах зубчато-подобных

проявлений возрастает. Начало падения напряжения происходит в точке а . Последующие падения происходят в точках времени б и в . Замечено, что «микро-фронт» последующего за точками а , б , в возрастания напряжения имеет тот же самый наклон к оси времени, т.е. одинаковую крутизну фронта (пунктирные линии параллельны).

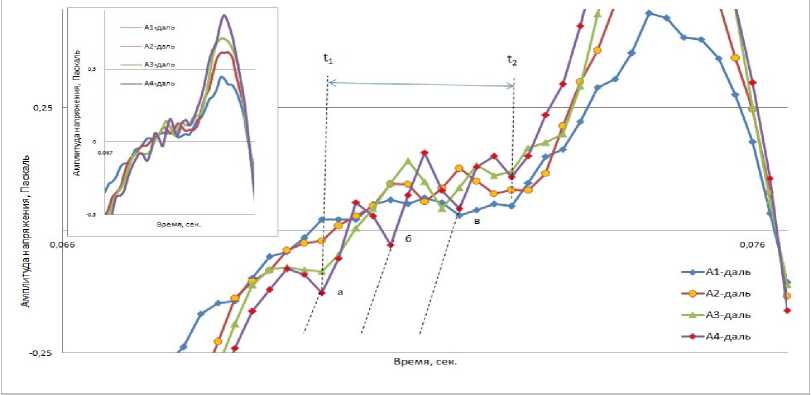
Рис. 6. Записи импульсов на четырех величинах амплитуды, зарегистрированные на расстоянии 14 м от источника и глубине 1 м

Fig. 6. Pulse records at four amplitude values recorded at a distance of 14 m from the source at a depth of 1 m

Обсуждение

Изучение сейсмических записей о( t ) показало, что форма волны осложнена вставками в виде плато скачкообразного изменения амплитуды напряжения. Такой эффект предположительно отнесен к проявлению скачкообразной прерывистой неупругости, обусловленной микропластичностью горных пород. Многочисленные данные в физике твердого тела и материаловедении также указывают на механизм пластичности и скачкообразной деформации [1; 3; 6; 9;14; 29; 27; 33]. Экспериментально показано, что процесс микропластичности по своей природе является амплитудно-зависимым [16, 37, 22, 25]. Прерывистое изменение амплитуды в форме сейсмического импульса аналогично остановке напряжения при достижении им критической величины о cr на кривой с ( е ) [28]. Эффективная крутизна фронта импульса

формируется при совместном участии упругости и неупругости скачкообразного характера. Это совпадает с данными, полученными в материаловедении. Внезапное появление плато текучести на кривых а ( е ) , названное как внезапный прыжок смещения при нагрузке и разгрузке («pop-in» и «pop-out event»), обнаружено во многих экспериментах [12; 21].

Дублирование записей, регистрация сигнала с накоплением обеспечивает достоверность измерений и снимает причастность помех произвольного характера. Повторная запись в пределах одного кванта времени не всегда совпадает с первой записью, как, например, показано на рис. 4. Это допустимо для записи с высокой детализацией в слож-нопостроенном материале, таком как горная порода. Эффект одинакового наклона локального участка на фронте волны после локального падения напряжения (рис. 6, парал-

MINING SCIENCE AND TECHNOLOGY лельные пунктирные линии из точек а, б, и в) предсказан в работе [14]. Здесь показано, что после участков падения напряжения на диаграмме о(а) следуют участки упругой деформации, которые являются параллельными друг другу. Также известен переход плато в падение напряжения (их взаимная замена), который показан на рис. 4, в. Необходимо отметить, что восходящий фронт импульса на всех амплитудах имеет осложнения, в то время как падающий фронт свободен от них (см. рис. 6). Входной импульс всегда также является практически «чистым».

Скачкообразная деформация и плато напряжения обнаружены также в природных материалах, таких как кремний [32], стишовит [30], сапфир, диорит, графит, слюда и другие [10]. Кварцевые зерна и другие минералы присутствуют как в твердых породах, так и в слабоконсолидированной среде. С помощью электронной микроскопии показано, что монокристаллы кварца содержат включения различного химического состава микрометровых размеров. При распространении волны малой интенсивности кварц обладает признаками неклассической неупругости, что зарегистрировано на параметрах амплитудно-частотно-зависимого затухания с применением электронной микроскопии [22]. Примечательным является тот факт, что скачки деформации и плато были обнаружены в таком слабом материале, как наноглина (nanoclay) [15], а также в гипсе [13] и граните. Эти факты тоже можно расценить как косвенное подтверждение возможности проявления таких эффектов в слабо консолидированной среде. Теоретическое обоснование распространения сейсмических волн с привлечением процесса микропластичности сделано в работе [36]. Необходимо рассмотреть и другие возможные механизмы, как например, акусто-пластический эффект в металлах и сплавах [28]. В этой работе был проанализирован экс-

периментальный материал и предложены обоснования и подходы решения проблемы механизма скачкообразной неупругости в горных породах.

Заключение

Новые данные о физике распространения сейсмических волн в реальной среде получены в этой работе. Имеется множество механизмов затухания сейсмических волн, однако механизм прерывистой (скачкообразной) деформации пока не включен в сейсмическую модель. Новые знания могут быть использованы для развития реологической модели и теоретических исследований. Вполне вероятно, что амплитудная зависимость скоростей волн и затухания связана с прерывистой неупругостью и, в частности, с микропластичностью. Об этом свидетельствует скачкообразный и стрессозависимый характер процесса деформации. Причиной трансформации формы волны может быть микропластичность.

Проблема природы микропластичности в геологических материалах остается пока открытой. Механизм неупругости может быть тем же самым, что и в твердых телах (движение дислокаций и других дефектов микроструктуры), или совершенно другим. Однако обнаруженные проявления сейсмомикропластичности в суглинках очень похожи на проявления микропластичности в обычных твердых телах. Этот вопрос требует дальнейшего прояснения. Микропластичность задевает малоизвестные неупругие процессы распространения малоамплитудных волн в природных материалах. Новые знания об упруго-неупругих процессах необходимы не только для развития теории, но и для получения более эффективных диагностических признаков при решении различных прикладных задач сейсмическими и акустическими методами.

MINING SCIENCE AND TECHNOLOGY

MINING SCIENCE AND TECHNOLOGY

seismoacoustic waves. Acoustic Physics, 45 (6), pp. 720–726.

MINING SCIENCE AND TECHNOLOGY

seismoacoustic waves. Acoustic Physics, 45 (6), pp. 720–726.