Эффекты слагаемых высшего порядка малости в обобщенных рядах для представления полей, ассоциированных с вершиной трещины в анизотропных средах. Часть 1. Сравнение точного и асимптотического решений определения напряжений у вершины трещины

Технологические композитные материалы, древесина, горные породы и костные ткани представляют собой примеры сред, демонстрирующих принципиальную анизотропию присущих им механических свойств: модули упругости, коэффициент Пуассона, объемный модуль, прочность и вязкость разрушения [1-14]. Анизотропные материалы имеют широкий спектр приложений, включая авиационные и космические композиционные элементы конструкций, авто- и судостроение, атомную энергетику, медицинское протезирование, спортивный инвентарь, эксплуатацию сланцевых коллекторов с помощью техники гидроразрыва пласта, осадочные фундаменты и деревянные конструкции и сооружения [1]. В некоторых из этих приложений, таких как композитные конструкции, проблема состоит в сохранении целостности и живучести системы, в то время как в других случаях, таких как гидроразрыв пласта, цель состоит в создании трещин определенной протяженности и направления. Вследствие этого изучение трещин, имеющихся в анизотропных средах, играет решающую роль в оценке прочности и живучести конструкций [1-14]. Основы теории упругости анизотропного тела заложены в [2], где сформулированы фундаментальные положения и концепции механики анизотропной линейно упругой среды и приведена систематическая формулировка плоской задачи теории анизотропных материалов в терминах аналитических функций комплексных переменных. С тех пор продолжаются исследования граничных задач механики твердого тела и механики разрушения, в частности [3—14]. По всей видимости, впервые решение задачи о растяжении бесконечной ортотропной плоскости с центральным разрезом было найдено в статье [3], развивающей более раннюю работу [4], где c применением классического формализма теории функции комплексного переменного (ТФКП) выведены общие уравнения для полей перемещений и напряжений вблизи острия разреза в анизотропной линейно упругой плоскости. В [4] получены соотношения для КИН непосредственно из функций напряжений Эри. Некоторые аналитические решения отдельных граничных задач даны в замкнутом виде и обсуждаются со ссылкой на сопутствующие им решения для изотропных тел. Обнаружено, что сингулярность, присущая данному подходу теории упругости анизотропного тела и свойственная линейно упругому материалу вида r-1/2, всегда присутствует у вершины трещины в теле с прямолинейной анизотропией (r - расстояние от фронта трещины). Полученный результат и дополнительный анализ полей напряжений у вершины трещины [3] ясно показал, что возможно распространить современные методы механики разрушения на представление условий разрушения для анизотропных тел с трещиноподобными дефектами. Одним из наиболее интересных результатов теоретических рассмотрений и численного расчета в [3] является четкое указание на зависимость коэффициентов интенсивности ортотропных напряжений от упругих постоянных. Для краевых задач такого типа коэффициенты интенсивности изотропных напряжений не зависят от материальных констант. Авторы [5] исследовали упругую реакцию на разрушение ортотропной пластины с наклонной трещиной, подвергнутой на бесконечности двухосной равномерной нагрузке. С этой целью предложен новый подход к получению выражений в терминах комплексных переменных для упругих полей в анизотропных пластинах. С использованием предлагаемой в [5] процедуры, основывающейся на каноническом подходе Колосова – Мусхели-швили, авторами получены распределения напряжений у вершины трещины, включающие неособые слагаемые и проанализировано влияние регулярных слагаемых на оценку угла роста трещины. Для прогнозирования угла распространения трещины был использован критерий максимального окружного напряжения с учетом того, что для ортотропных материалов необходимо учитывать зависимость критического КИН для режима I от угла, характеризующего анизотропию материала. С учетом неособых слагаемых изучены локусы разрушения ортотропных материалов, что еще раз подчеркнуло отличие поведения анизотропных материалов от изотропного случая и влияние неособых слагаемых. В целом теория разрушения анизотропных тел в настоящее время еще окончательно не отточена, продолжает активно и динамично развиваться и привлекает внимание представителей многих научных школ нашей страны [6–10] и мира [11–18]. Ярким примером анизотропного материала со сложной иерархической структурой является костная ткань. Понимание и математическое описание пространственной деформации и поведения кости при переломах остается важной задачей для расшифровки взаимосвязи между структурой, функцией и составом кости с целью улучшения стратегий профилактики переломов [11]. Целью исследования [11] является определение влияния формы наконечника индентора и ориентации ткани на характер растрескивания и локальную деформацию кортикальной кости при нагрузке вдавливанием и определение свойств локального разрушения, полученных на основе экспериментальных полей смещения вокруг трещин, вызванных вдавливанием. Авторы комбинируют поэтапные испытания на вдавливание SRμCT in situ (метод компьютерной микротомографии) и DVC (метод объемной цифровой корреляции изображений – один из наиболее популярных оптических методов, основная идея которого заключается в сравнении изображений объекта до и после деформации), чтобы изучить взаимосвязь между возникновением трещины и локальной деформацией в кортикальной кости овцы, количественно оценить смещения при раскрытии локальной трещины, режимы разрушения и коэффициенты интенсивности напряжений на концах трещин, вызванных вдавливанием, исходя из полей смещений, измеренных DVC.

В конечном счете это поможет оценить эластичность, пластичность и трещиноватость кости в зависимости от ее микроструктуры. В [11] представлена экспериментальная методика, сочетающая визуализацию с высоким разрешением, тестирование вдавливания индентора в кость и цифровую корреляцию объемов. Методика позволяет количественно оценить локальную деформацию, распространение трещин и режимы разрушения кортикальной кости. Результаты исследования подчеркивают анизотропное поведение костной ткани, состоящей из остеонов, сложный рисунок распространения трещины и демонстрируют разрушения, инициируемые сложными напряженными состояниями под острием индентора. Это представляет широкий интерес не только для понимания переломов костей, но и для понимания другой архитектуры биоструктур, обеспечивая эффективный способ количественной оценки механизмов их упрочнения в связи с их основной механической функцией. При подземной разработке горных пород естественные дефекты (такие как трещины, стыки, полости произвольной формы) и анизотропия горного массива являются решающими факторами, влияющими на прочность конструкции [12]. Расчет коэффициентов интенсивности напряжений анизотропных упругих тел с множеством овальных отверстий и трещин имеет первостепенное значение не только для проектирования запорных отверстий для повышения стабильности эксплуатации горных выработок, но и для оптимизации параметров гидроразрыва пласта для повышения производительности использования геотермального и (или) сланцевого газа. Текущие исследования в основном сосредоточены на нагружении удаленными напряжениями, независимо от поверхностных напряжений, приложенных к отверстиям и трещинам. В работе [12] учитываются как удаленные однородные напряжения, так и неоднородные поверхностные напряжения для расчета многотрещинных систем, взаимодействующих с множеством овальных отверстий в анизотропных упругих твердых телах. На основе интегрального подхода Коши ТФКП аналитически выведены два элементарных решения для сдвиговых составляющих напряжений вблизи одиночного овального отверстия и одиночной трещины, подверженных воздействию поверхностных точечных сил в анизотропной среде. В статье предложен новый подход для решения задачи, сводящейся к интегральным уравнениям, описывающим систему взаимодействующих овальных отверстий и трещин в двумерных анизотропных упругих твердых телах без каких-либо ограничений по количеству, размерам, ориентации и местоположению овальных отверстий и трещин [12]. Его точность и осуществимость подтверждаются путем сравнения полученных решений КИН с доступными точными решениями, приближенными решениями и решениями с использованием метода конечных элементов. Новый метод может быть дополнительно обобщен на случай трехмерной анизотропной задачи «отверстие – трещина» при тех же сложных напряженных состояниях.

Поэтому можно заключить, что большинство натуральных и искусственно созданных материалов прояв- ляют анизотропию своих механических свойств, которую необходимо принимать во внимание при характеристике процессов разрушения. На первоначальном этапе анализа явления разрушения и определения напряженно-деформированного состояния в теле с разрезом часто обращаются к приближенным (асимптотическим) соотношениям для полей вблизи трещины, что диктует, в свою очередь, необходимость определения неизвестных коэффициентов рядов вблизи кончика разреза с помощью теоретической, экспериментальной или численной процедуры. Коэффициенты первых слагаемых рядов, стоящие при r 12, именуемые КИН, получили первенствующее значение в доктринах механики упругого разрушения [1; 8-10; 14; 15]. В силу чего до сих пор в многочисленных исследованиях представителей различных научных школ довлеет именно определение исключительно КИН (или КИН и Т-напряжений) [1; 12; 13]. Вместе с тем на значительных дистанциях от кончика трещины сингулярные слагаемые не характеризуют в полной мере поля в окрестности вершины разреза, и влияние параметров линейной механики упругого разрушения высшего порядка становится очевидным [1; 810; 14; 15]. Многие примеры и исследования [1; 8-10; 14-16] свидетельствуют о необходимости учета регулярных (неособых) слагаемых, членов более высокого порядка малости [1; 8-10; 14-16]. Эти параметры полезны при анализе траектории роста трещины и механизма разрушения анизотропных сред в тех случаях, когда зона процесса велика по сравнению с длиной трещины. Используя эти данные о параметрах механики разрушения более высокого порядка, можно не только улучшить аналитические представления для напряжений, деформаций и смещений, но и расширить и уточнить уже существующие критерии разрушения.

Опираясь на вышеуказанные источники, можно утверждать, что анализ полей, ассоциированных с кончиком трещины в анизотропных телах, представляет собой одну из определяющих проблем современной механики разрушения. Настоящая работа посвящена изучению эффектов высших приближений в обобщенном представлении полей напряжений, деформаций и перемещений в анизотропных средах.

Фундаментальные соотношения плоской задачи теории упругости анизотропных сред

Условие совместности деформаций плоской задачи для анизотропной среды в терминах функции напряжений Эри имеет вид [1; 2; 6]

^S 22 ^Ф , 1111 ^{2 S} 26 ^Ф , 1112 ^{+ ( 2 S} 12 ^{+ S} 66 ^)Ф , 1122

^{2 S} 16 ^Ф , 1222 ^{+ S} 11 ^Ф , 2222 = ⁰ ,

где S j , i , j = 1,2,6 - компоненты тензора податливости анизотропного материала в плоской задаче:

Ге Ь 11		S 11    S 12    S 16	' ^ 11 ^
е 22	=	S 12    S 22   S 26	^ 22	.               (2)
ч 2 6 12 >		ч S 16    S 26   S 66 2	1 ° 12 >

Если внести определяющие соотношения (2) в условие совместности 2 е ₁₂₁₂ =e_{B 22} +е ₂₂ц, то можно получить уравнение относительно функции напряжений Эри (1), решение которого представляют в форме комплексного потенциала Ф ( x 1 , x ₂) = Ф ( z ), вводя в рассмотрение комплексную переменную z = x 1 + y x ₂, что приводит к характеристическому уравнению

S up⁴ - 2 S ^ц ³ + ( 2 S 12 + S 66 ) Р ² — ² S 26 Р+ S 22 = 0. (3)

Четыре корня характеристического уравнения (3) связаны с упругими постоянными материала соотношениями [9; 10]:

^Р 1 ^Р 2 ^Р 3 ^Р 4 = ^S 22 / ^S 11 , ^Р 1 ^Р 2 ^Р 3 ^{+ Р} 2 ^Р 3 ^Р 4 ^{+ + Р} 3 ^Р 4 ^Р 1 ^+Р 4 ^Р 1 ^Р 2 = ^{2 S} 26 / ^S 11 ,

Р1Р2 +Р2Р3 +Р3Р4 +Р1Р3 +Р4Р1 +Р2Р4 =

= ( 2 S 12 + S 66 ) / S 11 , Р 1 + Р 2 +Р з +Р 4 = 2 S 16 / S 11 .

Уравнение (3) отражает зависимость решения от упругих постоянных материала. Ранее было показано [9], что корни характеристического уравнения (3) являются комплексными величинами и всегда появляются в комплексно-сопряженных парах:

Р 1 =Р 1 + i 8 1 , Р 2 =р 2 + i § 2 , Р з =Р 1 , Р 4 =Р 2 - (4)

Здесь i - мнимая единица, черта сверху означает комплексное сопряжение. В частном случае изотропной линейно упругой среды Р 1 = ц ₂ = i . Большинство анизотропных материалов имеют плоскости и оси симметрии их упругих свойств, что приводит к снижению числа независимых упругих постоянных материала. Хорошо известно [2], что ортотропные среды имеют три ортогональные плоскости симметрии, и для описания упругих свойств требуется девять постоянных. Ниже рассматривается случай ортотропного материала и считается, что плоскость пластины совпадает с одной из плоскостей симметрии упругих свойств. Рассматривая плоскую задачу теории упругости анизотропного тела, введем две главные оси в плоскости пластины, относительно которых упругие свойства среды симметричны. Пусть x[, x 2 -главные оси в плоскости пластины. В случае плоского напряженного состояния требуется только четыре упругие постоянные [1; 2]: модули Юнга E 1 , E ₂ вдоль главных осей x ‘ , x 2 , модуль сдвига G ₁₂ и коэффициент Пуассона v ₂₁. Компоненты S ij. в главных осях имеют вид:

2 1/E1    -v21/ E2     0 2

• —V 12 / E 1    1/ E 2        0    .

. 0          0      1/ G ₁₂ ,

Тогда характеристическое уравнение (3) принимает форму:

ц' ⁴ + ( E 1 /G 12 - 2 v 21 E 1 /E 2 ) ц' ² + E 1 /E 2 = 0.     (5)

Таким образом, характеристическое уравнение содержит четыре независимые упругие константы. Во многих случаях в дальнейшем анализе различные авторы [1; 13; 14; 16] прибегают к дополнительным упрощающим гипотезам, базируясь на принципе Сен-Венана. Принимается, что справедливо приближенное соотношение 1 / GSV = 1/ E1 +1/ E2 + 2v21 / E2, связывающее упругие константы. В действительности модуль сдвига G12 является независимой материальной константой и может отличаться от G1s2v . В [1] приведены экспериментальные обоснования данного факта, и авторы фактически прибегают к рассмотрению анизотропной среды, характеризуемой двумя материальными параметрами ^ = E1/ E2 и П = G12 / Gi2 ■ Поэтому в [1] анизотропию материала описывают только два параметра ^ и п. Чем более параметры ^ и п отличаются от единицы, тем сильнее анизотропия механических свойств рассматриваемой среды. Если параметр п существенно отличается от единицы, то использовать подобное упрощение нельзя. В настоящее время методы молекулярной динамики (МД) и под- ходы, основанные на идее «из первых принципов» (ab initio), позволяют вычислить упругие константы материа- лов, поэтому имеется возможность оперировать непосредственно полным набором упругих модулей, не прибегая к дополнительным упрощениям, и вычислить непосредственно корни характеристического уравнения (3) [1]. Поэтому, в отличие от подхода, применяемого в [1], в настоящей работе характеристическое уравнение (3) для кубической сингонии исследовалось без указанных упрощений, а материальные постоянные (элементы тензора упругих модулей) для кубической симметрии вычислялись с помощью метода молекулярной динамики. Таким образом, при анализе полей напряжений и деформаций в окрестности вершины трещины использовались данные МД вычислений для монокристаллических меди и алюминия. Подробное описание вычислений приведено в [9; 10]. Значения упругих модулей для ГЦК меди и алюминия следующие:

'162  115  115  0    0    0

115  162  115  0    00

115  115  162  0    00

0    0    0    81   00

0    0    0    0    810

.0    0    0    0    0    81

'118  88   88   0    0    0

88   118  88   0    00

88   88   118  0    00

0    0    0    45   00

0    0    0    0    450

L0    0    0    0    0    45

Упругие свойства монокристаллов меди и алюминия проиллюстрированы на рис. 1–3, полученных с помощью открытого программного обеспечения ELATE [20].

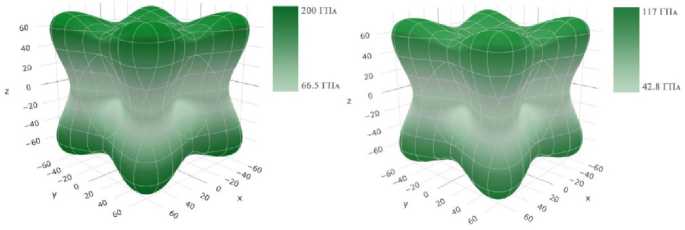
a                                                       b

Рис. 1. Пространственная визуализация модуля Юнга для меди ( a ) и алюминия ( b )

Fig. 1. 3D visualization of Young’s modulus for copper ( a ) and aluminium ( b )

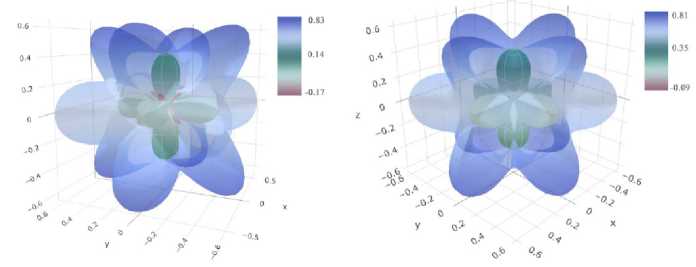
a

b

Рис. 2. Пространственная визуализация коэффициента Пуассона для меди ( a ) и алюминия ( b )

Fig. 2. 3D visualization of Poisson’s ratio for copper ( a ) and aluminium ( b )

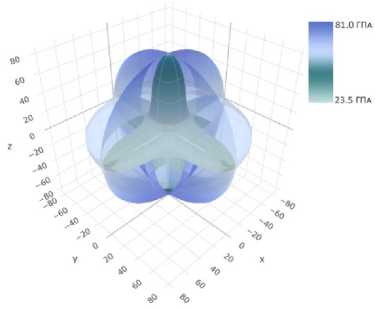
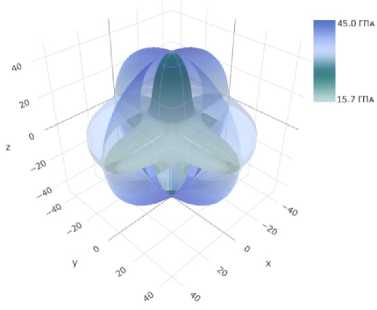
Рис. 3. Пространственная визуализация модуля сдвига для меди ( a ) и алюминия ( b )

Fig. 3. 3D visualization of shear modulus for copper ( a ) and aluminium ( b )

b

Поля напряжений у вершины трещины в плоской задаче теории упругости анизотропных сред

Изучение механических полей вблизи вершины трещины в анизотропных телах восходит к работе Си, Пэриса и Ирвина [4], в которой с использованием теории функций комплексного переменного получены общие уравнения для перемещений и напряжений у вершины трещины в анизотропной пластине. В [4] определен КИН у вершины математического разреза с учетом свойств анизотропии среды. В рамках использованных предположений найдено, что у кончика разреза в плоскости с прямолинейной анизотропией свойств всегда присутствует сингулярность напряжений порядка r ^{- 1/}2 ( r - радиальное расстояние от фронта трещины). Полученные результаты рассмотрения полей напряжений у вершины трещины привели авторов к заключению, что можно обобщить развитые методы механики разрушения изотропных сред на представление условий разрушения для анизотропных тел с трещиноподобными дефектами. На основе ТФКП в [1; 5] получены выражения для комплексных потенциалов, отвечающих деформации отрыва и сдвига, бесконечной плоскости с центральной трещиной (рис. 4).

Для двух различных корней характеристического уравнения, что обычно справедливо для анизотропных сред, решение уравнения (1) разыскивается с помощью двух функций F ₁ и F ₂ комплексных переменных z ₁ и z ₂ :

Ф = 2Re [ F ( z 1 ) + F ₂( z ₂) ] ,

Z 1 = X 1 + R 1 x 2 ,

z 2 = X i + R ₂ x 2 ■

Подстановка представления (6) в (1) и введение новых функций Ф 1 ( z 1 ) = dF 1 l dz 1 , Ф ₂ ( z ₂) = dF 2 / dz ₂ позволяет представить решение в форме:

^ ii = 2 Re ^Ф’ ( z 1 ) + Ц 2 Ф 2 ( z 2 ) ] , G 22 = 2 Re [ Ф‘ ( z 1 ) + Ф 2 ( z 2 ) ] , ^ 12 =— 2 Re [r Ф’ ( z j ) + Ц 2 Ф 2 ( z 2 ) ] ■

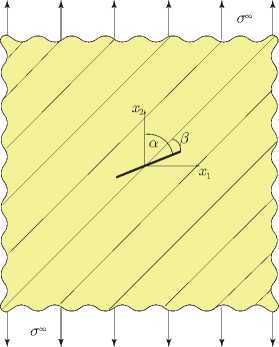
Рис. 4. Геометрия рассматриваемой анизотропной пластины, ослабленной центральной трещиной, где α – угол между ориентацией трещины и направлением действия растягивающей нагрузки, β – угол между трещиной и осью симметрии упругих свойств среды

Fig. 4. The schematics of an infinite anisotropic plate with an inclined central crack where α is the angle between the crack line and loading direction, β is the angle between the anisotropy orientation and the crack line

Компоненты тензора деформаций и вектора перемещений определяются выражениями:

E 11 = ^{2 R}e E а ^ф ‘ ^{( z} i ), ^e 22 = ^2Re E q i R i ^Ф ‘ ^{( z} i ), i = 1                                       i = 1

e12 = 2 Re E di RiФ ‘ (zi), i=1

u 1 = ^{2 Re} E р ^ф i ⁽ z ), u 2 = ^{2 Re} E q i ^ф i ⁽ z )■ i = 1                                   i = 1

Здесь приняты следующие обозначения: P j = ^ 11 ^R 2 - ^S 16 ^R j ^{+ S} 12 , q j = ^S 12 ^R j - ^S 26 ^{+ S} 22 / ^R j , d j = = S ₁₆ R _j - S 66 + S ₂₆ / R _j ■ Структура комплексных потенциалов имеет вид [1]:

Ф 1 ( z 1 ) = о ” ( р ₂ sin² а + sin a cos а ) х

^Х [ z 1 - z^2--²^ ] / [ 2 ( ^р 1 -М- 2 ) ] ^{+ Г} 1 z 1 ,        (7)

z 1 = x 1 + р 1 x 2 ,

Ф 2 ( z 2 ) = -о ” ( м 1 sin² а + sin а cos а ) х

^Х[ z 2 ^— "\/ z 2 - a ] / ^[ 2 ^(М 1 -^р 2 ^{)] + Г} 2 z 2 ’         ⁽⁸⁾

Z 2 = Х1 + р2 X 2, в которых коэффициенты могут быть определены точно с помощью формул (7)–(10):

A = ( 41a / 4 ) о ” sin² а , B 1 = ( 41a / 8 ) о ” sin2 а , В ₂ =

= о ” Re ( р 1 +р ₂ )( sin2 а- 2 Х ) / 4Im ( р ₁ р ₂ ) ,

A ₂ = о ” ( cos² а + Re ( р 1 р ₂ ) sin² а + + Х Re ( р 1 +р ₂ ) ) /2 Im ( р 1 +р ₂ ) ,

A3 = (3/8-j2a )о” sin2 а, где приняты обозначения:

В 3 = ( 3/8j2a ) о ”

sin а cos а ,

Г 1 = -о ” { р ₂ sin² а + sin а cos а +

+ i р ₂ [ Re ( р 1 +р ₂ )( sin а cos а-Х ) /Im ( м 1 р ₂ ) +

+ ( cos² а + Re ( м 1 р ₂ ) sin² а +

+ Х Re ( р 1 + р 2 ) ) / [М 2 Im ( р 1 + р 2 ) ]^] } /2 (р, -Р 2 ) ,

Г ₂ = о ” { р 1 sin² а + sin а cos а +

+ i р 1 [ Re ( р 1 +р ₂ )( sin а cos а-Х ) /Im ( р 1 р ₂ ) + + ( cos² а + Re ( р 1 р ₂ ) sin² а +

+ Х Re ( р 1 +р ₂ ) ) / [р 1 Im ( р 1 +р ₂ ) ]] } /2 ( р 1 -р ₂ ) .

В выражениях (9), (10) Х - вещественный параметр, зависящий от величины перемещения тела как твердого тела, о ” - величина приложенной нагрузки, a - половина длины трещины. На основе формул (7)–(10) может быть выведено асимптотическое поле напряжений у вершины трещины в ортотропном линейно упругом материале в форме рядов [1]:

			■           ( - 1) к + | + 1 р 2 р 1  2 ( - 1) к + 1 - р 2 р 2 2	к - 1 ( cos G + Р 2 sin 0 ) 2 - + 1                               к - 1 ( cos 0 + р 1 sin 0 ) 2
о '	■ = 2Re •	”        -( к + 1)2     к j	( - 1) к + 1 + 1 р 1 2     (	„       . „ к - 1 cos 0 + Р 2Sln 0 ) 2 -
о 22		Z Ак-----r 2
о 2 .		Ы    р 1 -р 2	( - 1) к + 1 + - р 2 2 ( - 1) к + 1 + - р 2 р 1  2 ( - 1) к + 1 _ + р 1 р 2 2	z                „к - 1 ( cos 0 + р 1 sin 0 ) 2 1                         к - 1 ( cos 0 + Р 2 Sln 0 ) 2 + + 1                               к - 1 ( cos 0 + р 1 sin 0 ) 2

■+

( - 1) k + ¹                              к - 1

р ² р 1 ²    ( cos 0 + р ₂sin 0 ) ² -

+ 2Re ^

”        •( к + 1) 2

Z Вк---- t1 р1-р2

(-1) k +i

- р 2 р ₂ ² ( cos 0 + р ₁sin 0 ) 2

(-1) k+1

р 1 ² ( cos 0 + р ₂sin 0 ) 2 -

(-1) к+1

- р ₂²    ( cos 0 + р ₁sin 0 ) ²

(-1)к+i

-р ₂ р ₁²    ( cos 0 + р ₂sin 0 ) ² +

(-1)к+i

+ р 1 р ₂ ² ( cos 0 + р ₁sin 0 ) 2

A 2 n + 2 = 0,   В 2 n + 2 = 0,

A 2 n ₊ 3 = ( - 1) n ^{+ 1} о ” sin² а [- 4 • ( 2 n - 1 ) !/ (2 n )! + + (2 n + 1)!/ (2 n + 2)! ] / [ 8(2 a ) ^{n + 1/2} ] , В _{2 n + 3} = ( - 1) n ^{+ 1} о ” sin а cos ах х [- 4 • ( 2 n - 1 ) !/ (2 n )! + (2 n + 1)!/ (2 n + 2)! ] / [ 8(2 a ) ^{n + 1/2} ] .

Формулы для компонент тензора напряжений (11) совместно с соотношениями (12), (13) для ОКИН формируют мультипараметрическое представление напряжений, ассоциированных с вершиной трещины в анизотропном линейно упругом теле. Асимптотическое представление (11)–(13) дает возможность проанализировать влияние регулярных (неособых) слагаемых в зависимости от расстояния от вершины дефекта.

Асимптотический анализ

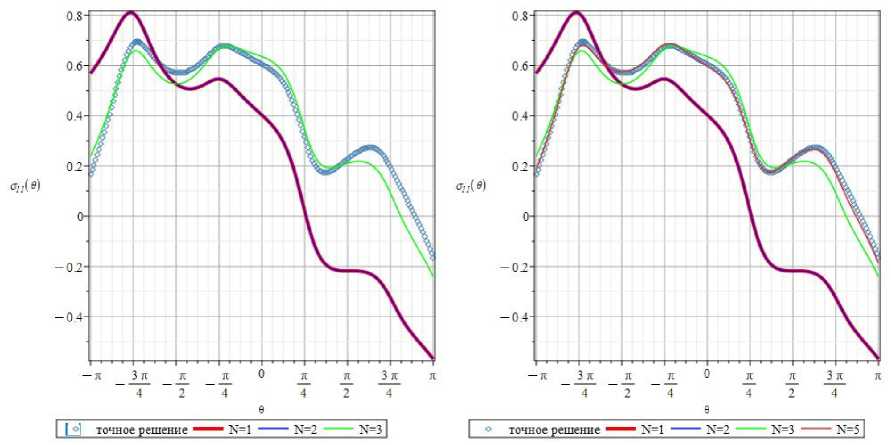
В настоящее время многокомпонентное асимптотическое разложение напряжений, ассоциированное с вершиной трещины, стало рабочим инструментом для целостного описания механических полей у концентратора напряжений [22–40]. Аналитическое решение, базирующееся на основе общих положений теории функции комплексного переменного, дает возможность провести строгую оценку вклада и влияния высших приближений (регулярных слагаемых) в общее описание поля напряжений и ответить на вопрос: сколько слагаемых ряда (11) следует удерживать для практических целей, например, при обработке экспериментальных данных, полученных интерференционно-оптическими методами в механике трещин? Используя мультипараметрические решения, можно дать оценку количества слагаемых, необходимых для воспроизведения точного решения. Имеющееся точное аналитическое решение задачи (6)–(10) и приведенное асимптотическое представление поля напряжений вблизи вершины трещины в анизотропной среде (11)– (13) предоставляют возможность оценить вклад регулярных слагаемых в обобщенных рядах (11)–(13). Естественно, начать анализ с трещины нормального отрыва (а = П /2), расположенной вдоль одной из осей симметрии упругих свойств (Р = 0) . Ниже приведены графики угловых зависимостей компонент напряжений от величины угла (окружные распределения) для различных расстояний от кончика разреза. На рис. 5 построены θ-зависимости нормальной напряжения σ11(r,θ) у острия трещины типа I вдоль окружности радиуса rˆ =r/a=0,77 с центром в кончике дефекта.

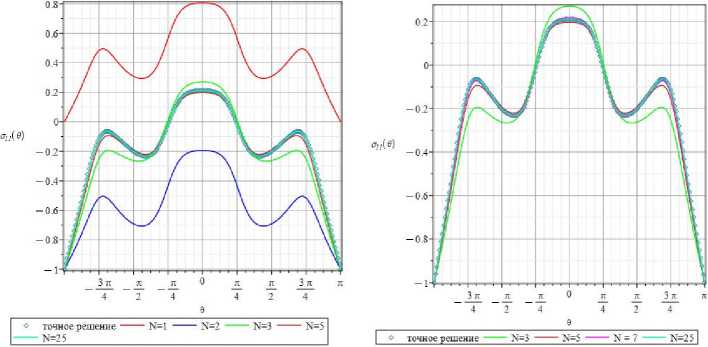
На рис. 5 слева показаны угловые зависимости компоненты тензора напряжений σ11(r, θ), найденные с помощью одночленного (красная кривая), двучленного (синяя кривая) и 25-членного (бирюзовая кривая) асимптотических разложений (11). Ромбами показано точное аналитическое решение, полученное с помощью соотношений (6)–(10). Очевидно, что одночленное и двучленное представления компоненты тензора напряжения σ11 (r, θ) существенно разнятся и значительно отличаются от точного решения, поэтому в асимптотическом разложении необходимо учесть следующие слагаемые. Трехчленное разложение показано на рис. 5 справа зеленым цветом. Вновь сравнение трех представлений для компоненты σ11 (r, θ) приводит к необходимости рассмотрения следующих слагаемых ряда (11). На рис. 6 показаны окружные распределения компоненты σ11 (r, θ), полученные посредством сохранения 5 и 7 слагаемых ряда (11). Из рис. 6 слева следует, что 3- и 5-членные асимптотические разложения значительно ближе друг к другу. Тем не менее кривые визуально отличаются друг от друга, и требуется удержание слагаемых более высокого порядка малости. На рис. 6 справа показаны кривые, обусловливаемые 3,5,7,25-членными рядами, для компоненты σ11(r, θ), и аналитическое решение. Данные рис. 6 свидетельствуют, что, несмотря на близость 5-членного и 7-членного рядов, визуально θ -распределения продолжают отличаться как друг от друга, так и от точного решения. Следовательно, необходимо прибегнуть к 9-членному асимптотическому ряду (рис. 7).

На рис. 7 приведены θ -зависимости компоненты σ ₁₁ ( r , θ ), найденные посредством 1, 2, 3, 5, 7,9- и 1, 2,3, 5, 7, 9, 11-членных представлений (11). Различия между 7- и 9-членными разложениями еще сохраняются, в то время как различия между 9- и 11-членными разложениями и точным решением практически отсутствуют. Строгие количественные оценки вклада высших приближений будут приведены во второй части статьи. Компонента тензора напряжений σ ₁₁ ( r , θ ) содержит Т-напряжение и, следовательно, можно было бы утверждать, что значительные отличия между угловыми распределениями, приведенными на рис. 5–7, обусловлены влиянием Т-напряжения. Однако аналогичные распределения, построенные для касательного напряжения σ ₁₂ ( r , θ ) и нормального напряжения σ ₂₂( r , θ ), ясно показывают, что влияние высших приближений оказывается важным и для других компонент тензора напряжений, которые не содержат Т-напряже-ний. На рис. 8 показаны построенные с удержанием 1, 3 и 1, 3, 5, 7 слагаемых ряда θ-зависимости касательного напряжения σ ₁₂ ( r , θ ) вдоль окружности радиуса r ˆ = r / a = 0,77 от кончика разреза.

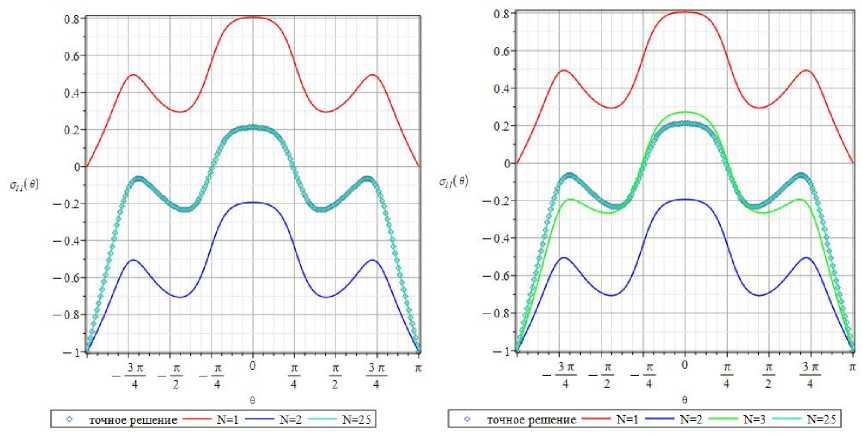
Рис. 5. θ-распределения компоненты σ ₁₁( r , θ ) вдоль окружности радиуса r ˆ = r / a = 0,77 с центром в вершине разреза, образованные с использованием 2 и 3 слагаемых ряда. Ромбами показано точное решение задачи, основанное на теории функции комплексного переменного

Fig. 5. θ-dependences of σ ₁₁( r , θ ) for the radius r ˆ = r / a = 0.77 obtained by the two and three term series. The rhombuses illustrate the exact solution based on the complex variable theory

a

b

Рис. 6. 0-зависимости нормального напряжения o_n ( r, 0 ) вдоль окружности r = 0,77 с центром в вершине трещины, найденные при удержании 5, 25 ( a ) и 7, 25 ( b ) слагаемых в асимптотическом разложении. Ромбами показано точное решение

Fig. 6. 0-dependences of O_n ( r , 0 ) for the radius r = 0.77 obtained by the 5.25 ( a ) and 7.25 ( b ) term series. The exact solution based on the complex variable theory is shown in rhombuses

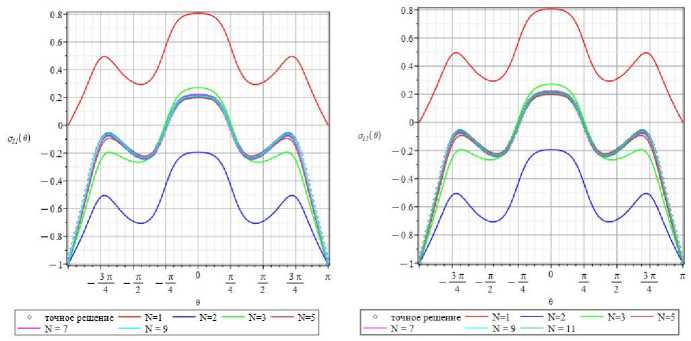
Рис. 7. 0-зависимости напряжения O_n ( r , 0 ) вдоль окружности радиуса r = r / a = 0,77 от вершины, построенные при удержании

1, 2, 3, 5, 7, 9 и 1, 2,3, 5, 7, 9, 11 слагаемых в разложении

Fig. 7. 0-dependences of the stress o_n ( r , 0 ) for the radius r = r / a = 0.77 obtained by the 1, 2, 3, 5, 7, 9 and 1, 2, 3, 5, 7, 9, 11 term series expansion

a

b

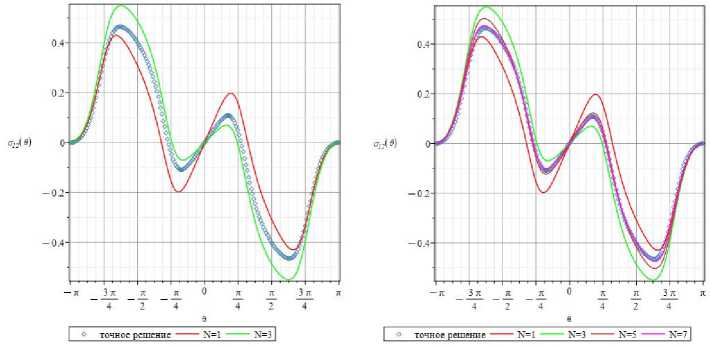
Рис. 8. Угловые зависимости касательного напряжения о ₁₂( r , 0 ) вдоль окружности радиуса r = r / a = 0,77 , построенные при удержании 1,3 ( a ) и 1,3,5,7 ( b ) членов ряда

Fig. 8. 0-dependences of the shear stress o ₁₂( r , 0 ) for the radius r = r / a = 0.77 obtained by the 1,3 ( a ) and 1, 3, 5, 7 ( b ) term series expansions

На рис. 8 слева красным цветом показано одночленное разложение, зеленым цветом – 3-членное асимптотическое разложение касательного напряжения, ромбами показано точное решение. Видно, что одночленное и 3членное распределения явственно отличаются друг от друга. На рис. 8 справа дополнительно показаны зависимости компоненты напряжения от полярного угла, определяемые 5-членным (кривая оранжевого цвета) и 7членным (кривая сиреневого цвета) асимптотическими разложениями. Все четыре кривые, определяемые приближенным решением (11), приведенные на рис. 8, b , заметно отличаются друг от друга и свидетельствуют, что на данном расстоянии от кончика трещины важно сохранять следующие слагаемые в асимптотическом разложении касательного напряжения. Из рис. 9 ясно, что с увеличением числа сохраняемых слагаемых разложения угловые зависимости становятся ближе друг к другу, однако на рис. 9 можно наблюдать видимые различия между 7- и 9-членным представлениями касательного напряжения. На рис. 9, а , в дополнение показана 0 -вариация касательного напряжения, определяемая 11-членным асимптотическим рядом (11). Из рис. 9 ( а ) явствует, что кривые, определяемые 9- и 11-членным разложениями, визуально неразличимы. Следовательно, на расстоянии r = r / a = 0,77 от вершины трещины необходимо удерживать 11 слагаемых (количественные оценки будут приведены во второй части статьи).

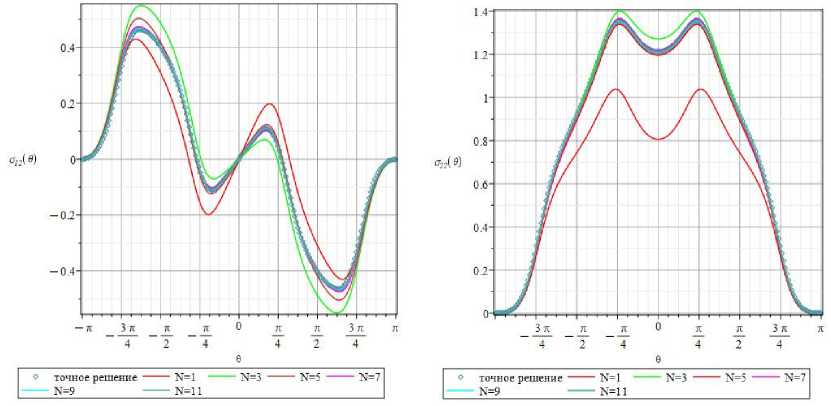
Для оставшейся нормальной компоненты тензора напряжений 022 (r, 0) выявляются те же отличительные особенности. На рис. 9 (b) показаны окружные зависимости компоненты 022 (r, 0) на расстоянии r = r / a = 0,77 от кончика трещины. Из рис. 9 видно, что ни одночленного, ни 3-членного рядов недостаточно для целостного описания компоненты тензора напряжений. Необходимо особо подчеркнуть, что второе слагаемое в разложении (Т-напряжение) для компоненты о22( r, 0) обращается в нуль. Оно не оказывает влияния на угловое поведение компоненты, поэтому на рис. 9 не изображены кривые, даваемые обобщенными двучленными разложениями. Из рис. 9 явствует, что на избранном значении радиуса необходимо удерживать слагаемые более высокого порядка малости. На рис. 9 в дополнение продемонстрированы окружные распределения нормального напряжения 022 (r, 0), образованные 7-, 9- и 11-членными разложениями. Для избранного значения радиальной координаты 7- и 9-членные асимптотические ряды визуально еще разнятся между собой (но, в целом, отличия между 7- и 9-членными рядами для данной компоненты менее заметны по сравнению с другими компонентами), поэтому необходимо удерживать следующие слагаемые. На графиках (рис. 9) дополнительно представлена угловая зависимость, построенная посредством 11-членного разложения и показанная зеленым цветом. Кривые, образованные с помощью 9- и 11-членных разложений, визуально практически не являются отличимыми между собой и от точного решения, поэтому для зрительного сравнения в данном случае достаточно сохранять 11 слагаемых обобщенного ряда (11). Даже на основании только визуального сопоставления окружных распределений компоненты 022 (r, 0) можно утверждать, что для избранного значения радиальной координаты r = r / a = 0,77 слагаемые высшего порядка играют заметную роль, и для совпадающего с точным решением приближенного асимптотического представления поля напряжений, ассоциированного с вершиной, необходимо удерживать 11 слагаемых ряда.

a                                                   b

Рис. 9. ©-распределения касательного напряжения о ₁₂( r , 0 ) ( а ) и о ₂₂( r , 0 ) ( b ) для радиуса r = r / a = 0,77, построенные при удержании 1, 3, 5, 7, 9 и 11 слагаемых ряда

Fig. 9. 0-dependencies of the shear stress component o ₁₂( r , 0 ) ( а ) and O ₂₂( r , 0 ) ( b ) for the radius r = r / a = 0.77 obtained by 1, 3, 5, 7, 9 and 11-term series expansions

Для выявления характерных отличительных особенностей и закономерностей θ-распределений компонент напряжений, представляемых мультипараметри-ческими рядами (11), ниже рассматривается увеличенное расстояние от вершины трещины и анализируются окружные θ-зависимости для каждой из компонент тензора напряжений. Построенные окружные θ-распреде-ления компоненты О 11 ( r , 0 ) вдоль окружности радиуса r = r / a = 1,25 с центром в вершине трещины показаны на рис. 10.

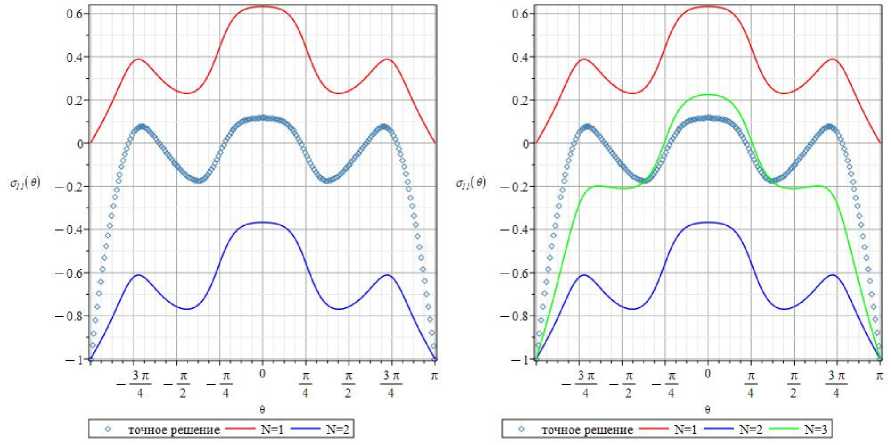
На рис. 10 ( a ) визуализированы θ-зависимости компоненты О 11 ( r , 0 ), образованные посредством сохранения 1 и 2 слагаемых ряда (11), и точное решение, базирующееся на ТФКП. С увеличением значения радиуса, для которого строится напряжение, различия между 1-и 2-членным разложениями усиливаются (по сравнению с рис. 5, а ). Остаются принципиальными различия и для 3-членного ряда, представленного на рис. 10, b . Из сопоставления кривых, приведенных на рис. 10, b , становится понятным, что должно сохранять следующие члены ряда (11).

b

Рис. 10. 0-зависимости напряжения o_n ( r , 0 ) для радиуса f- = 1,25 , образованные при помощи 1, 2- ( а ) и 1, 2, 3-членных ( b ) рядов

Fig. 10. 0-dependencies of the stress component O_n ( r , 0 ) for the radius r = 1.25 given by 1,2 ( а ) and 1, 2, 3 ( b ) term series expansions

a                                                   b

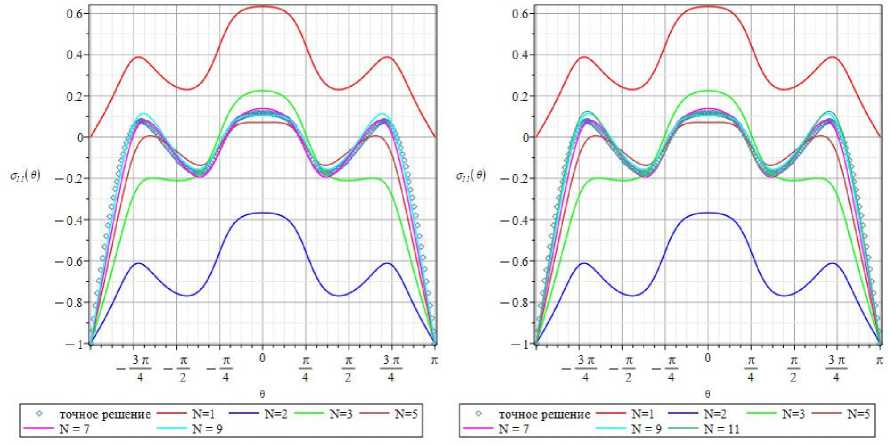
Рис. 11. 0-зависимости составляющей o_n ( r , 0 ) для радиуса r = r / a = 1,25, полученные с помощью 1, 2, 3, 5, 7, 9 ( a ) и 1, 2, 3, 5, 7,

9, 11-членных разложений ( b )

Fig. 11. 0-dependencies of the stress O_n ( r , 0 ) for the radius r = r / a = 1.25 given by 1, 2, 3,5, 7, 9 ( a ) and 1, 2, 3, 5, 7, 9, 11 ( b ) term series

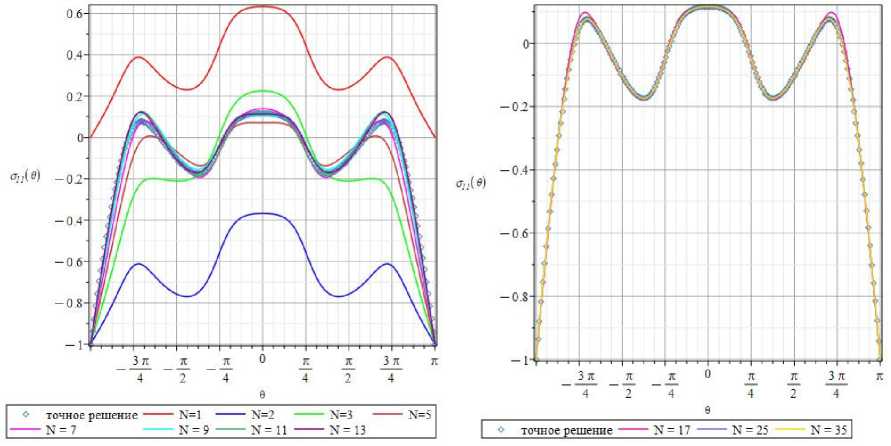
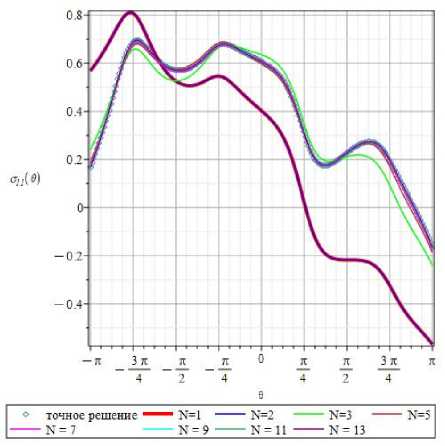
На рис. 11 проиллюстрированы θ-зависимости напряжения О11( r, 0) вдоль окружности радиуса r = 1,25 с центром в вершине трещины, найденные с помощью 1,3,5,7,9- и 11-членных рядов, представляющих О11(r, 0). По сравнению с данными на рис. 6, 7, где приведены те же окружные распределения, но на меньшем расстоянии r = 0,77 от вершины трещины, различия между угловыми распределениями увеличиваются. Из рис. 11 ясно, что различия между 7- и 9-членными асимптотическими разложения значительны и требуется сохранение следующих слагаемых. Кривые, иллюстрирующие окружные распределения, построенные на основании 9- и 11-членного разложений, продолжают отличаться друг от друга (рис. 11, b), что делает необходимым рассмотрение 13-членного асимптотического ряда (11). Из рис. 12, a, где проиллюстрированы θ-зависимости нормального напряжения О11( r, 0) в окружном направлении для радиуса r = 1,25, полученные с помощью 1, 2, 3, 5, 7, 9, 11, 13 сохраняемых членов ряда (a) и 17, 25 и 35 оставляемых членов ряда и базирующегося на ТФКП решения (b), следует, что ряда с 13 слагаемыми не является достаточно для целостного описания напряжения. На графиках рис. 12, b, показана кривая, построенная на основе точного решения теории упругости анизотропного тела. Визуальное сопоставление кривых рис. 12, b, снова подтверждает, что для целостного описания компоненты тензора напряжений Gn(r, 0), совпадающего с точным решением, для значения радиальной координаты r = 1,25 требуется не менее 25 слагаемых.

Схожие особенности, свойственные многопараметрическому асимптотическому ряду для о_п( r , 0 ), проявляет 0-распределение касательного напряжения о ₁₂ ( r , 0 ). На рис. 13 проиллюстрированы θ-зависимости касательного напряжения о ₁₂( r , 0 ) на расстоянии r = r / a = 1,25, найденные с помощью 1-, 3- и 5-членного разложений (11). Характерная черта, наблюдаемая ранее для компоненты G_n( r , 0 ), прослеживается и для касательного напряжения о ₁₂( r , 0 ) : кривые, построенные с помощью 1- и 3-членного разложения, принципиально различаются. Кривая, полученная с помощью 5-членного разложения, также далека от ранее построенных кривых.

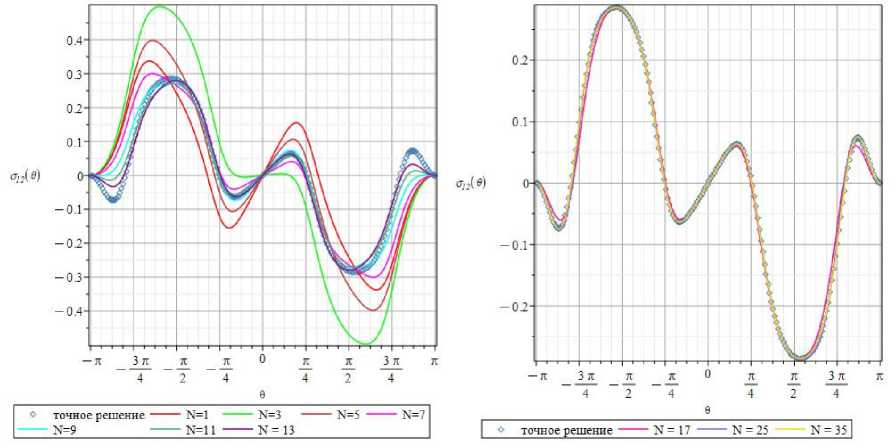
На рис. 14, а , проиллюстрированы типичные окружные зависимости касательного напряжения о ₁₂( r , 0 ) для значения радиальной координаты r = 1,25, построенные с помощью 1, 3, 5, 7, 9, 11- и 13-членных асимптотических рядов. Видно, что 13 слагаемых асимптотического ряда не позволяют получить кривые, сходящиеся к предельной кривой (точному аналитическому решению). 0 - распределения касательного напряжения о ₁₂ ( r , 0 ), даваемое 11- и 13-членными разложениями, показанные на рис. 14, а , зеленым и фиолетовым цветом соответственно, становятся существенно более близкими друг к другу. Однако данные представления все еще визуально заметно отличаются друг от друга.

a                                                   b

Рис. 12. 0-зависимости составляющей o_n ( r , 0 ) на расстоянии r = r / a = 1,25 от вершины трещины, полученные с помощью 1, 2, 3, 5, 7, 9, 11, 13- ( а ) и 17, 25, 35-членных рядов компоненты тензора напряжений и точного аналитического решения ( b )

Fig. 12. 0-dependencies of the stress component O_n ( r , 0 ) for the radius r = r / a = 1.25 given by the 1, 2,3,5, 7, 9, 11, 13 term series ( а ) and the 17, 25, 35 term series and the exact solution ( b )

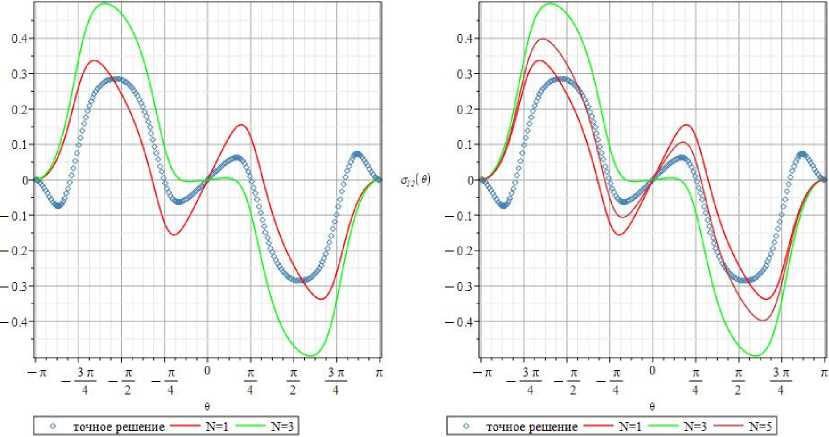
Рис. 13. 0-зависимости касательного напряжения о12( r, 0) для r = r / a = 1,25, найденные посредством 1, 3- и 5-членных рядов

Fig. 13. The 0-variations of the shear stress O ₁₂( r, 0 ) for Г = r / a = 1.25 found by 1, 3, 5 term series

a

b

Рис. 14. Окружные зависимости ( а , b ) касательного напряжения О ₁₂( r , 0 ) для r = 1,25, производимые 11- и 13-членными асимптотическими рядами

Fig. 14. The 0-variations ( а , b ) of the shear stress O ₁₂( r , 0 ) at r = 1.25 given by 11 and 13 term expansions

На рис. 14, b , представлены угловые распределения касательного напряжения на расстоянии r = r / a = 1,25 , в которых сохранены 17, 25 и 35 слагаемых. На рис. 14 проиллюстрировано точное аналитическое решение, базирующееся на теории упругости анизотропных сред. Компаративный анализ показывает, что на избранном расстоянии от острия трещины кривая, найденная с принятием во внимание 17 слагаемых ряда, видимо, отличается от точного решения, базирующегося на представлениях ТФКП. Кривая, определяемая 25-членным рядом и показанная на рис. 15, b , практически совпадает с точным решением, но все еще видны визуальные отличия.

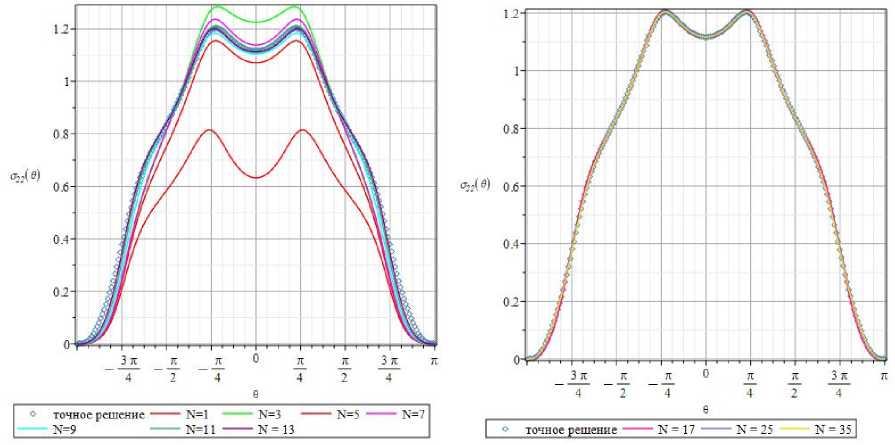
Вместе с этим угловое распределение, даваемое 35-членным рядом, неотличимо от точного аналитического решения. Схожая картина наблюдается для нормальной составляющей напряжения о ₂₂ ( r , 0 ): одночленное и трехчленное асимптотические разложения существенно различаются (см. рис. 15), что приводит к потребности удержания высших приближений. На рис. 15, а , построены θ-зависимости нормальной компоненты о ₂₂( r , 0 ) вдоль окружности радиуса r = r / a = 1,25, определяемые 1, 3, 5, 7, 9, 11-и 13-членным асимптотическими рядами.

b

Рис. 15. Окружные зависимости напряжения О ₂₂( r , 0 ) вдоль окружности радиуса r = r / a = 1,25 : 1, 3, 5, 7, 9, 11, 13-членное ( а ) и 17, 25, 35-членные ( b ) асимптотические ряды

Fig. 15. The 0-dependences of the stress component O ₂₂( r , 0 ) for the radius r = r / a = 1.25 from the crack tip: 1, 3, 5, 7, 9, 11, 13 term series expansions ( a ) and 17, 25, 35 term expansions ( b )

Кривые, иллюстрирующие θ - зависимости нормального напряжения o ₂₂( r , 0 ) вдоль окружности радиуса r = r / a = 1,25, определяемые 17-, 25- и 35-членными асимптотическими рядами, изображены на рис. 15, b . Данные рис. 15 снова подтверждают четкую тенденцию: эффект влияния неособых (регулярных) слагаемых усиливается с увеличением расстояния от кончика трещины, где проводится анализ θ - распределений.

Данные, приведенные на рис. 15, убедительно показывают, что на расстоянии / " = r / a = 1,25 от кончика трещины необходимым является удержание не менее 25 слагаемых ряда.

Асимптотический анализ смешанного нагружения

При рассмотрении комбинированного деформирования интересен случай расположения трещины под углом а = п / 4 , поскольку в этом случае Т-напряжение обращается в нуль и можно оценить вклад следующих слагаемых без влияния Т-напряжений. На рис. 16 приведены θ-рас-пределения нормальной компоненты Оп (r = 0,77a, 0) для угла наклона трещины к вертикали, равного а = п / 4 , построенные с помощью 1-, 3- и 5-членного асимптотических рядов (11) и точного решения (6)–(10) (все значения напряжений отнесены к приложенному растягивающему напряжению). Из рис. 16 (а) видно, что графики, построенные посредством 1- и 3-членного разложений, значительно отличаются друг от друга и от точного решения. На рис. 16 (b) приведена кривая, полученная с помощью 5-членного ряда компоненты он. Несмотря на сохранение пяти слагаемых в разложении, кривые визуально разнятся, и ясно, что необходимо рассматривать следующие члены разложения.

На рис. 17 ( a ) продемонстрированы угловые зависимости универсальных функций в разложении поля напряжений (11), показывающие, что на выбранном расстоянии 7-, 9- и 11-членное разложения отличаются друг от друга. Кривая, построенная с помощью 13-членного разложения (рис. 17, b ), становится визуально не отличимой от кривой, полученной посредством 11-членного ряда. Для ответа на вопрос, сколько слагаемых следует удерживать в разложении на указанном расстоянии от вершины, необходимо задать требуемую точность и провести количественные оценки, что будет выполнено во второй части статьи.

На рис. 18 приведены угловые зависимости компоненты тензора напряжения о12. На рис. 18 (а) показаны кривые, определяемые 1, 3, 5, 7, 9- и 11-членным рядами. Из рис. 18 (b) явствует, что однопараметрическое и трехпараметрическое представления касательного напряжения в значительной степени разнятся и необходимо обратиться к слагаемым более высокого порядка малости. На рис. 18 (a) представлено 5-членное асимптотическое разложение касательного напряжения, также существенным образом отличающееся от трехчленного разложения, что свидетельствует о необходимости удержания следующих членов ряда. На рис. 18 представлены 7-и 9-членные асимптотические разложения касательной компоненты о12. Рис. 18 (b) показывает, что 7- и 9-членные разложения все еще отличаются друг от друга (количественные оценки будут приведены во второй части работы), и визуальный анализ позволяет видеть необходимость рассмотрения следующих членов ряда, 11-членный ряд практически совпадает с точным решением. На рис. 18 (b) приведено дополнительно 13-членное разложение касательной компоненты, сравнение которой с кривой, определяемой 11 слагаемыми, дает возможность увидеть, что кривые, определяемые 11 и 13 слагаемыми, совпадают. Точное число слагаемых, необходимых для сохранения в ряду, определяется требованиями достижения наперед заданной точности вычислений.

b

a

Рис. 16. 0-зависимости составляющей О_п тензора напряжения на расстоянии r = r / a = 0,77 , при удержании 3 ( а ) и 5 ( b ) слагаемых ряда

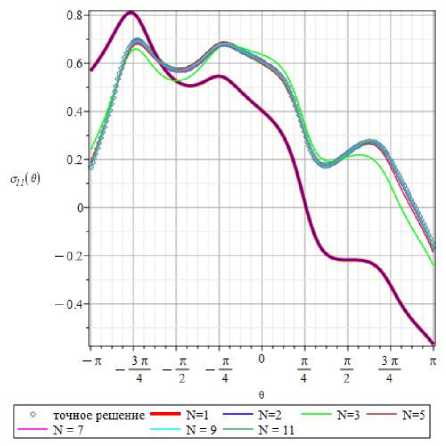
Fig. 16. The 0-dependencies of the stress component 0 11 for the radius r = r / a = 0.77 when three ( a ) and five ( b ) terms in the series expansion are kept

a                                                           b

Рис. 17. Зависимости составляющей 0 11 тензора напряжения от угловой координаты 0 на расстоянии r = r / a = 0,77 , при удержании 11 ( а ) и 13 ( b ) слагаемых ряда

Fig. 17. The 0-dependencies of the stress component 0 11 for the radius r = r / a = 0.77 when 11 ( a ) and 13 ( b ) terms in the series expansion are kept

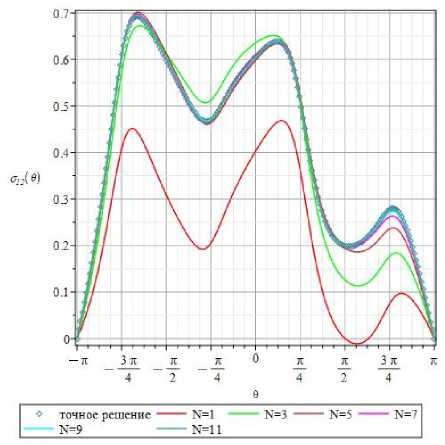
Рис. 18. 0-зависимости составляющей О _|2 тензора напряжения на расстоянии r = r / a = 0,77 , при удержании 1, 3, 5, 7, 9, 11 ( а ) и 13 ( b ) слагаемых асимптотического ряда

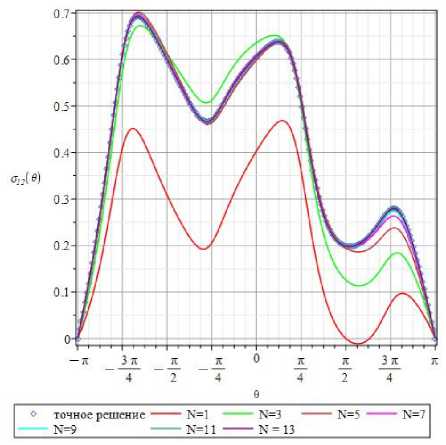
b

Fig. 18. The 0-dependencies of the stress component a ₁₂ for the radial coordinate r = r / a = 0.77 when 1, 3, 5, 7, 9, 11 ( a ) and 13 ( b ) terms in the series expansion are kept

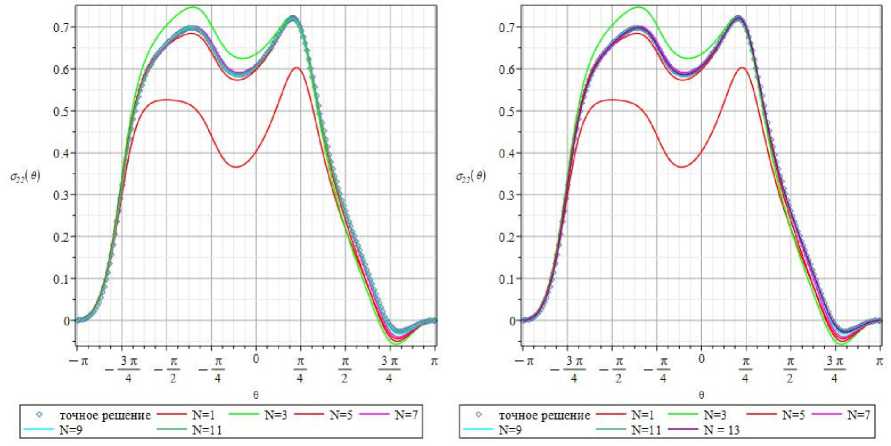
Из рис. 19, где показаны θ-распределения компоненты G 22 , явствует, что на избранном расстоянии от вершины дефекта 3- и 5-членные разложения существенным образом различаются. Для представления поля напряжений следует прибегать к многопараметрическому представлению, состоящему из большего числа слагаемых. На рис. 19 также показаны угловые распределения, построенные посредством 7 и 9 слагаемых. На рис. 19 ясно продемонстрировано, что 7- и 9-членные разложения становятся значительно ближе друг к другу, но все еще заметно визуально разнятся (сиреневая и голубая кривые). Если рассматривать 11- и 13-членное разложения компоненты о ₂₂ (см. рис. 19), видно, что с увеличением числа сохраняемых слагаемых кривые стремятся к предельной кривой (к точному решению задачи). Тем не менее визуально различия между кривыми, соответствующими 11 и 13 слагаемым, представляющим решение, заметны на рис. 19, b , и вновь количество слагаемых, оставляемых в разложении, обусловлено требуемой точностью.

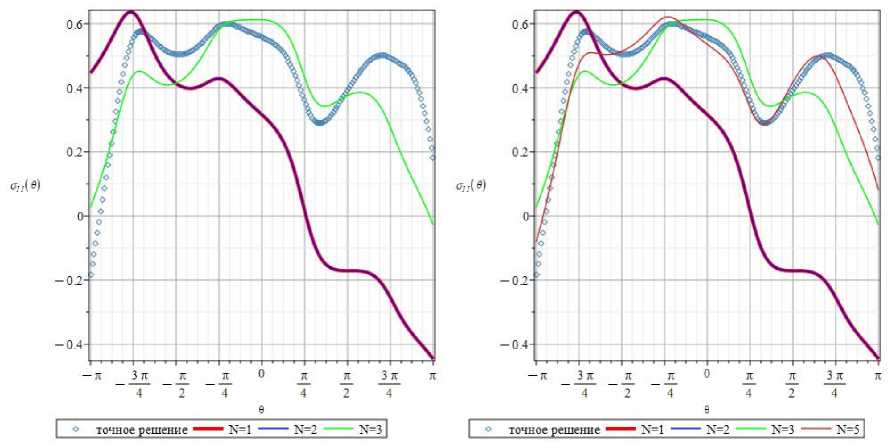
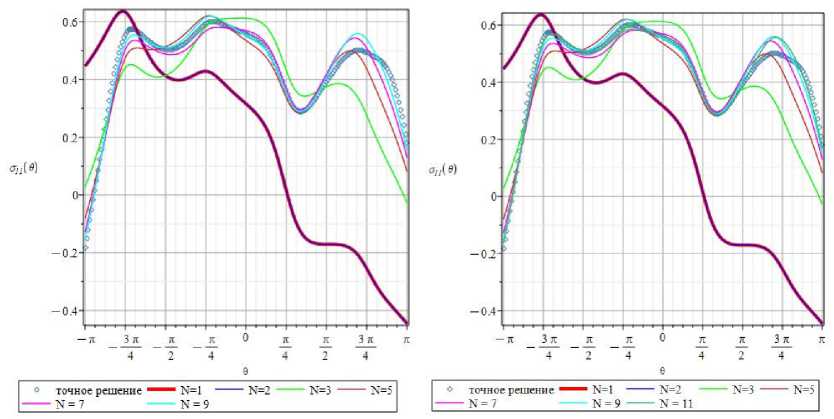
Необходимость точного представления и строгого анализа полей деформаций и напряжений, ассоциированных с трещиной в анизотропной среде с кубической симметрией, на больших расстояниях от кончика дефекта обусловливает сохранение большего числа членов ряда. Для обоснования сформулированного заключения можно рассмотреть окружность радиуса r = r / a = 1,25 . На рис. 20, а, представлены распределения компоненты О11, полученные одночленным (красная кривая) и трехчленным (зеленая кривая) разложениями, точное решение представлено ромбами. На рис. 20, b, дополнительно изображена кривая, построенная с помощью пятичленного асимптотического представления компоненты оп (оранжевая кривая). Данные рис. 20 позволяют констатировать, что ни одного, ни трех, ни пяти слагаемых ряда недостаточно для описания компоненты О11 на указанном расстоянии. Учитывая вышеизложенное, следует сохранить большее количество слагаемых ряда (11). Построенные 9- и 11-членные разложения представлены на рис. 21, сиреневая и голубая кривая соответственно. Для выбранного расстояния от кончика трещины 9- и 11-членные ряды оказываются явственно различными.

На рис. 22 отражены различия между 11- и 13-членным разложениями компоненты О 11 для r = r / a = 1,25. Отчетливо видно, 13-членного разложения недостаточно для того, чтобы добиться визуального совпадения решений. Для выяснения числа слагаемых, необходимых для целостного представления напряжений, обратимся к рис. 22, b , где приведены 17-членное, 25-членное, 35членное разложения и точное решение, даваемое комплексными потенциалами (7) и (8). Сопоставление кривых и визуальное сравнение дают возможность заключить, что в асимптотическом решении следует удерживать по меньшей мере 35 слагаемых. Точное число слагаемых определяется требуемой наперед заданной точностью.

a

b

Рис. 19. 0-зависимости составляющей 0 22 тензора напряжения на расстоянии r = r / a = 0,77 при удержании 11 ( a ) и 13 ( b ) слагаемых асимптотического ряда

Fig. 19. The 0-distributions of the stress 0 22 for the radius r = r / a = 0.77, when 11 ( a ) and 13 ( b ) terms of the series are kept

b

a

Рис. 20. 0-зависимости нормальной составляющей 0 11 для радиуса r = r / a = 1,25 , при удержании 3 ( a ) и 5 ( b ) слагаемых в асимптотическом разложении

Fig. 20. The 0-dependencies of the stress component o_n for the radius r = r / a = 1.25 when 3 ( a ) and 5 ( b ) terms in the series expansion are kept

a

b

Рис. 21. 0-зависимости составляющей О_п тензора напряжения на расстоянии r = r / a = 1,25, при удержании 9 ( а ) и 11 ( b ) слагаемых асимптотического ряда

Fig. 21. The 0-dependencies of the stress component 0 11 for the radius r = r / a = 1.25, when 9 ( a ) and 11 ( b ) terms in the series expansion are kept

b

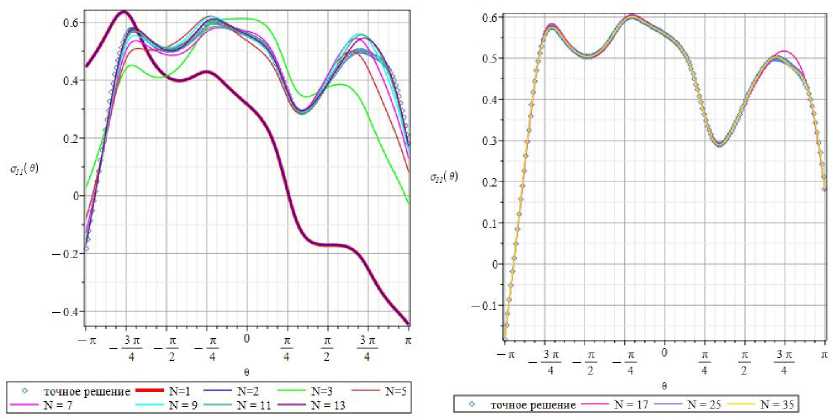
Рис. 22. Зависимости составляющей 0 11 тензора напряжения от угловой координаты 0 на расстоянии / ' = r / a = 1,25, при удержании

1, 3, 5, 7, 9, 11, 13 ( a ) и 17, 25 и 35 ( b ) слагаемых в асимптотическом разложении. Точное решение показано ромбами

Fig. 22. The 0-dependencies of the stress component 0 11 at distance r = r / a = 1.25 when 1, 3, 5, 7, 9, 11, 13 ( a ) and 17, 25, 35 ( b ) terms in the series expansion are kept. The exact solution based on the elasticity theory of anisotropic media is shown by rhombuses

Схожая картина наблюдается при сравнении многопараметрических разложений для касательного напряжения o ₁₂ на том же расстоянии r = r / a = 1,25 . На рис. 23 построены 1, 3- и 5-параметрическое разложения касательного напряжения на указанном расстоянии.

По сравнению с расстоянием r = r / a = 0,77, в этом случае различия между кривыми становятся более существенными и, очевидно, что ни однопараметрическое, ни трехпараметрическое разложения не могут правильно отразить зависимость касательного напряжения от полярного угла. В силу указанной причины необходимо сохранить высшие приближения. На рис. 24, а, продемонстрированы кривые, полученные при сохранении 1, 3, 5, 7, 9, 11, 13 слагаемых ряда, для касательного напряжения на расстоянии r = r / a = 1,25 от острия дефекта. На рис. 24, а, наглядно показаны различия между 7, 9, 11- и 13-членным разложениями касательного напряжения, где совместно построены 11-членное

(темно зеленая кривая) и 13-членное (фиолетовая кривая) разложения, и отчетливо видно, что эти кривые разнятся, и должно удерживать больше слагаемых в (11). Рис. 24, b, четко подчеркивает различия между 17- и 25членными разложениями. Совершенно очевидно, что для аккуратного описания поля напряжений надлежит рассмотреть регулярные члены ряда высоких порядков. Рис. 24, b, показывающий 0 -зависимости компоненты напряжений о12, определенные с сохранением 17, 25 и 35 слагаемых асимптотических рядов, и точного аналитического решения, базирующегося на решении теории аналитических функций (7) и (8), это дает возможность утверждать, что 1) с увеличением количества удерживаемых слагаемых кривые стремятся к точному решению; 2) визуального совпадения кривых можно достичь при сохранении 35 слагаемых ряда.

a

b

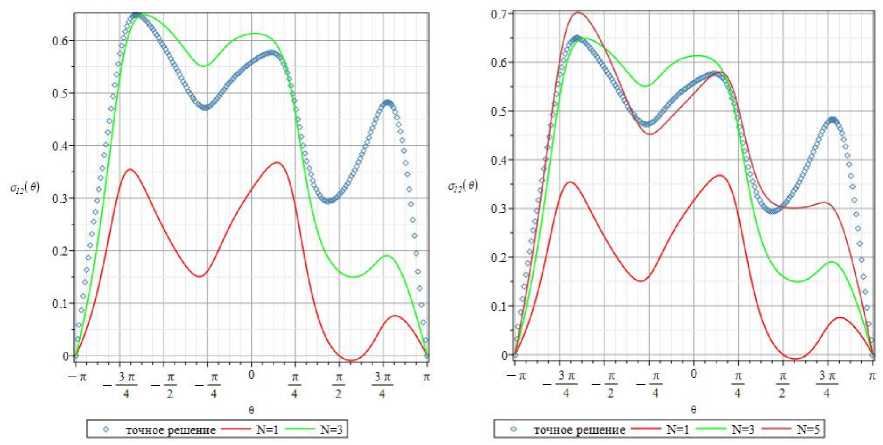
Рис. 23. Зависимости составляющей а ₁₂ тензора напряжения от угловой координаты 0 на расстоянии Г' = r / a = 1,25 , при удержании 1,3 ( а ) и 1,3,5 ( b ) слагаемых ряда

Fig. 23. The 0-dependencies of the stress tensor component a ₁₂ for the radius Г = r / a = 1.25 when 1,3 ( a ) and 1,3,5 ( b ) terms in the series expansion are kept

b

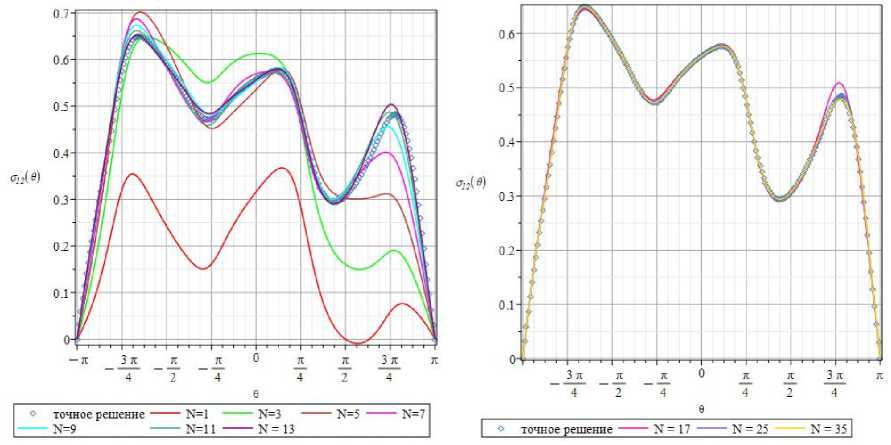
Рис. 24. Зависимости составляющей o ₁₂ тензора напряжения от угловой координаты 0 на расстоянии Г' = r / a = 1,25 , при удержании 1, 3, 5, 7, 9, 11, 13 ( а ) и 17, 25, 35 ( b ) слагаемых асимптотического ряда

Fig. 24. The 0-dependencies of the stress component o ₁₂ at distance Г = r / a = 1.25 when 1, 3, 5, 7, 9, 11, 13 ( a ) and 17, 25, 35 ( b ) terms in the series expansion are kept

b

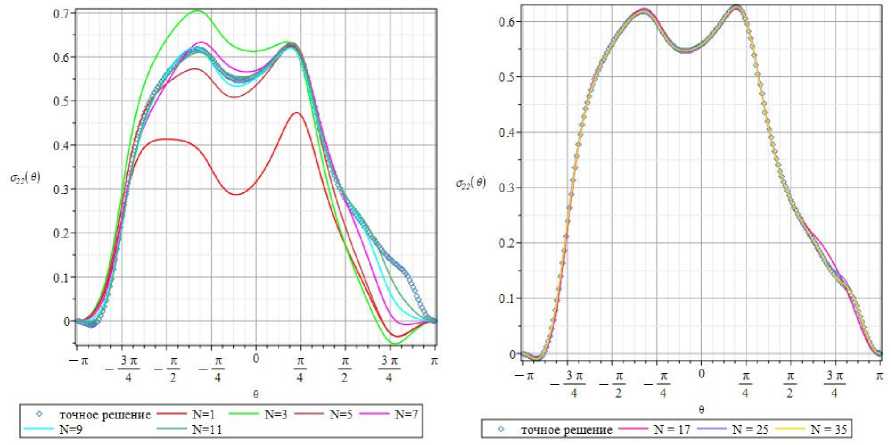
Рис. 25. Составляющая О ₂₂ тензора напряжения как функция угловой координаты 0 на расстоянии r = r / a = 1,25 при удержании 1, 3, 5, 7, 9, 11 ( а ) и 17, 25, 35 ( b ) слагаемых в асимптотическом разложении и точное решение задачи, основанное на теории упругости анизотропных сред

Fig. 25. The 0-dependencies of the stress component o ₂₂ at distance r = r / a = 1.25 when 1, 3, 5, 7, 9, 11 ( a ) and 17, 25, 35 ( b ) terms in the series expansion are kept

Данные на рис. 25 подтверждают вышеприведенные рассуждения на примере компоненты тензора напряжений o ₂₂. Из рис. 25 следует, что различия между 1-и 3-членным разложениями напряжения становятся более существенными, по сравнению с дистанцией r = r / a = 0,77 от вершины трещины. Рис. 25 показывает вклад высших приближений на представление поля напряжений в анизотропной пластине с трещиной.

Рис. 25 ( b ) показывает, что только 25 слагаемых ряда воспроизводят полностью точное распределение компоненты о ₂₂ . Основной вывод, который может быть сформулирован после выполненного сравнительного анализа, состоит в необходимости обращения к многочленным асимптотическим разложениям, особенно в тех случаях, когда требуется оценить и проанализировать поля вблизи трещины на расстояниях порядка половины длины трещины.

Заключение

Проведен анализ рядов, представляющих напряжения и перемещения у вершины острого разреза в плоской анизотропной среде с кубической сингонией (симметрией) упругих свойств, и впервые для материалов с кубической симметрией их упругих свойств построены угловые распределения компонент напряжений для различных значений радиальной координаты (на различном удалении от вершины дефекта), при учете различного количества сохраняемых слагаемых ряда для нормального отрыва и смешанного (комбинированного) деформирования образца с трещиной. На основании построенных окружных распределений составляющих тензора напряжений на различных расстояниях от кончика разреза разъяснен вклад регулярных слагаемых в общее представление поля напряжений. Рассмотрен общий случай, характеризующийся двумя углами, представляющих собой угол между ориентацией трещины и направлением действия растягивающей нагрузки и угол между трещиной и осью симметрии упругих свойств среды соответственно. Основная черта, присущая асимптотическим разложениям полей напряжений, ассоциированным с вершиной трещины, состоит в том, что регулярные слагаемые становятся значимыми с увеличением расстояния от кончика трещины и позволяют существенно расширить область, где справедливо асимптотическое решение задачи. Отличительной особенностью выполненного анализа угловых распределений напряжений является использование рассчитанных методом молекулярной динамики компонент тензора упругих модулей для монокристаллических гранецентрированных меди и алюминия. Вычисления были реализованы в открытой программе, реализующей метод молекулярной динамики, Large-scale Atomic/Molecular Massively Parallel Simulator. Вычисленные постоянные материала дают возможность точного отыскания корней характеристического уравнения, не прибегая к дополнительным упрощениям, и позволяют получить уточненные угловые распределения напряжений. Построенные угловые распределения предоставляют возможность оценить влияние регулярных слагаемых на различных расстояниях от кончика трещины: регулярные слагаемые играют существенную роль в целостном описании поля напряжений.