Эффекты слагаемых высшего порядка малости в обобщенных рядах для представления полей, ассоциированных с вершиной трещины в анизотропных средах. Часть 2. Оценки точности асимптотических решений

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2025PNRPU MECHANICS BULLETIN

В механике хрупкого разрушения для аппроксимирования перемещений, деформаций и напряжений в близлежащей окрестности вершины надреза, трещины или острого углового выреза распространен метод разложения по собственным функциям, приводящий к асимптотическим представлениям (в виде асимптотических рядов по степеням r1/2 расстояния от кончика трещины r ) механических полей у вершины дефекта, к формальным бесконечным рядам [1–5]. Долгое время при решении краевых задач механики трещин сохраняли первые слагаемые рядов, соответствующих нормальному отрыву и поперечному сдвигу, которые содержат коэффициенты интенсивности напряжений, и Т-напряжения – коэффициенты доминирующих слагаемых в близлежащей окрестности вершины были основными рассматриваемыми величинами (параметрами разрушения) [6–12], в то время как последующими слагаемыми более высокого порядка малости при малых r пренебрегали. В последнее время удержание регулярных слагаемых в асимптотических рядах, аппроксимирующих поля у вершины трещины, особенно при обработке данных экспериментов, проводимых поляризационно-оптическими методами, конечно-элементными расчетами и иными численными методами (методом фазового поля), стало обычной рутиной [13–18]. Во многих исследованиях полей, ассоциированных с вершиной трещины, в настоящее время сохраняют 5–9 слагаемых или более [13– 18]. Однако, несмотря на большое количество исследований, реконструирующих асимптотический ряд М. Уильямса или его распространение на случай анизотропных сред [19–32], общих закономерностей, устанавливающих связь между рассматриваемыми расстояниями от кончика трещины, типом комбинированного нагружения (или углом наклона трещины), избранным материалом и расположением осей симметрии анизотропии, пока не предложено. Для анизотропных материалов, по всей видимости, таких оценок еще не получено. Поэтому количественная оценка погрешностей, допускаемая при усечении асимптотических рядов, представляющих поля перемещений, деформаций и напряжений вблизи вершины трещины, представляет самостоятельный интерес.

В настоящей работе оценка точности приближенного решения в форме обобщающего подход М. Уильямса ряда по степеням расстояния от кончика трещины в анизотропной среде производится с помощью двух подходов. Первый основан на вычислении полей абсолютной погрешности, даваемой приближенным асимптотическим рядом при его усечении на разном количестве слагаемых. Поля абсолютной погрешности построены для двух случаев: для усеченных 11-и 19-членных асимптотических рядов. Обнаруживается, что в окрестности вершины трещины существуют геометрические места точек, в которых абсолютная разность точного и приближенного решений имеет порядок 10—12 —10—14, то есть приближенное решение практически полностью воспроизводит точное, что может быть использовано при обработке экспериментальных данных, полученных из опытов, проводимых интерференционно-оптическими методами, и подходами, опирающимися на конечно-элементный анализ полей у вершины трещины в анизотропной среде. Второй подход основан на вычислении относительной погрешности в соответствии с введенной L2 -нормой. Данный подход позволяет для достижения желаемой точности выбрать необходимое количество слагаемых ряда в приближенном решении.

Поля абсолютных погрешностей

Известный формализм теории функций комплексного переменного (ТФКП) позволяет получить поля напряжений о_а₽ в анизотропной пластине с наклонной в общем случае трещиной в форме [4; 5]

°« о22

^О 12

+ 2Re

= 2Re

"

)² k

"         •( Л + 1) Л

Е A r²

Л =1

М^

"       .•( л + 1) 2

Е Вл-—■ Л = 1    М-М ₂

-— 1

—I

(—I) ' " +I                         Л _—          (—£2+1                         Л _—

Ц 2 Ц , ² ( cos 6+g ₂sin 6 ) 2 — Ц 2 Ц ₂ ² ( cos 9+ц^т6)2

g ² ( cos 6 + g₂ sin 6 ) ² 1 —ц 2 ² ( cos 9 + ц^т6 ) ² 1

(—1) ^{Л 1 1} + 1                                   л _— 1            (—1) ‘ ^{+ 1} + 1                                  Л _— 1

—Ц 2 Ц 1 ² ( cos 6+g 2 sin 6 ) ² +Ц 1 Ц 2 ² ( cos 9+ц^т6 ) ²

'        (—1)Л +1                                     л —1            (—1)Л +1

ц 2 М 1 ² ( cos 9+M 2 sin б ) ² — ц 2 ц 2 ² ( cos б+ц^т6 ) 2

(—1)Л+1                               л —1 (—1)Л+1

ц ² ( cos 6+M 2 sin 6 ) ² —М 2 ² ( cos б+ц^тв ) 2

(—1)Л+1                                     к —1            (—1)Л +1

—ц^ц ² ( cos 9+g 2 sin 9 ) ² +М 1 М 2 ² ( cos б+ц^т9 ) 2

. (2)

о_п=о ~ Re J —¹—

IМ 1 —М 2

, 1 sin ² a + sin a cos а ) . ^{2 2}= \ Z 2 ^— a

— ( ц₂ sin²а + sin a cos а

И 2 ^Z 1

> +

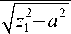
+ о " Г cos² а + Re ( ц 1 ц₂ ) sin² а + Re ( ц 1 + ц₂ ) sin а cos а

о 22 = ^а ™ Re

J — ( ц ₁ sin²а + sin а cos а )

I М 1 —М 2 '                        ⁷

z ₂

z 2 — a

—

( ц₂ sin²a + sin а cos а

z ₁

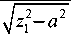
о₁₂ = о " Re

I —1^-2^-

<------ ( gj sin а + sin а cos а )

IИ1-И2 V                        7

М- 2 ^Z 2

Пг 2

z ₂— a

—

— ( ц₂ sin²a + sin а cos а

М 1 ^Z 1

2     2

V Z 1 — a

где приняты обозначения: z j = x 1 +g j x ₂- комплексные переменные, g j - корни характеристического уравнения, a - половина длины трещины, о " - приложенная нагрузка, а - угол между трещиной и вертикальной осью. Разложение напряжений (1) в ряд по степеням расстояния от кончика дефекта в полярных координатах с полюсом в вершине трещины приводит к асимптотическим рядам

В выражениях (2) A_k , B_k – коэффициенты ряда, отражающие влияние приложенных усилий и форму образца с трещиной или вырезом. Для простых конфигураций образцов коэффициенты могут быть найдены с помощью теоретического решения. К такому типу конфигураций относится бесконечная пластина с центральным математическим разрезом. Формулы для коэффициентов A_k , B_k получены в [4; 5] и обсуждались в первой части настоящей работы. Для более сложных форм образцов с более сложными системами нагружений требуется привлечение экспериментальных и вычислительных процедур для восстановления ряда (2) и его коэффициентов, при этом возникают вопросы, связанные с числом сохраняемых слагаемых ряда (2): сколько слагаемых ряда следует удерживать для достижения требуемой точности и чем это число обусловливается. Ответить на данные вопросы позволяет сопоставление точного решения (1) и приближенного решения (2) для краевых задач, допускающих точное теоретическое решение. Поэтому ниже рассматривается сравнение решений (1) и (2) для бесконечной анизотропной пластины, ослабленной наклонной центральной трещиной.

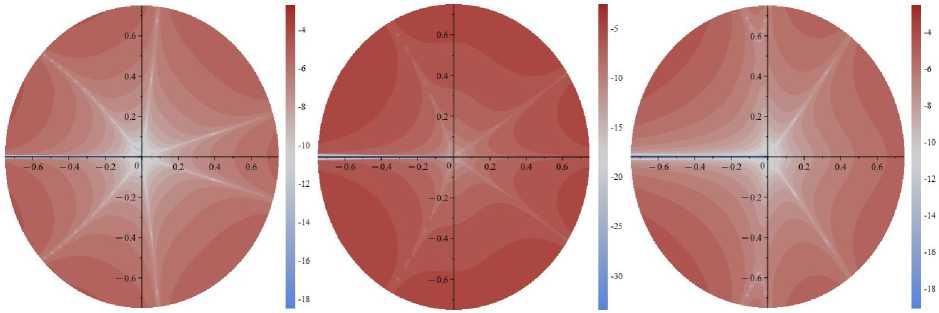
Для практических целей формальные асимптотические разложения (2) усекают, оставляя конечное число слагаемых. Для оценки ошибки, допускаемой усеченным рядом, можно рассмотреть абсолютную разность между точным аналитическим решением (1) и приближенным аналитическим решением в рядах (2). Для удобства ниже построены десятичные логарифмы от абсолютной погрешности для 11- и 19-членных рядов (2) для каждой компоненты. Выражения для коэффициентов ряда A_k , B_k приведены в первой части статьи. На рис. 1–8 проиллюстрированы распределения десятичного логарифма полей абсолютных погрешностей, допускаемых при усечении на 11 и 19 слагаемом асимптотических рядов, представляющих поля напряжений для нормального отрыва ( а = п / 2 ) и нескольких значений углов, отвечающих смешанному нагружению (а = 3п /8, а = п /4 и а = п /8, в = 0). На рис. 1-8 видны геометрические места точек, для которых абсолютная погрешность имеет порядок 10 ^{— 10} для компоненты о_п (см. рис. 1, слева), 10 ^{— 16} для компоненты о ₁₂ (см. рис. 1, в центре) и 10 ^{— 12} (для компоненты о ₂₂ (см. рис. 1, слева)) для асимптотических рядов, содержащих 11 слагаемых (7 ненулевых

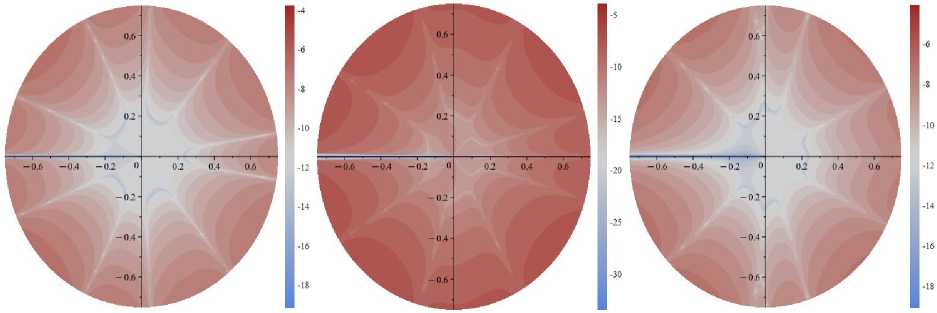
для σ ₁₁ и 6 отличных от нуля для σ ₁₂ и σ ₂₂ ). Эти геометрические места можно интерпретировать как точки точности асимптотического решения, в которых асимптотическое представление воспроизводит решение (1), построенное на основе методов ТФКП, с высокой точностью. На рис. 2 представлены десятичные логарифмы полей абсолютной погрешности для рядов с 19 слагаемыми для α=π/2. Видно, что число кривых с увеличением количества удерживаемых слагаемых растет. С ростом числа удерживаемых приближений допускаемая погрешность снижается и имеет порядок 10 ^{- 14}

для компоненты σ ₁₁ (см. рис. 2, слева), 10 ^{- 20} для компоненты σ ₁₂ (см. рис. 2, в центре) и 10 ^{- 16} (для компоненты σ ₂₂ (см. рис. 2, справа)). Для асимптотических рядов, содержащих 19 слагаемых, имеется 11 ненулевых для σ ₁₁ и 10 отличных от нуля для σ ₁₂ и σ ₂₂ . Ниже данные геометрические места точек с низкой абсолютной погрешностью называются локусами точности. На рис. 3 и 4 показаны точки точности решения (локусы точности) для смешанного нагружения пластины с наклонной трещиной при α=3π/8 для двух случаев: 11 и 19 слагаемых ряда.

^σ 11

^σ 12

^σ 22

Рис. 1. Поля абсолютных погрешностей, допускаемых усечением ряда на 11-м слагаемом для α=π/2 и σ ₁₁ (слева), σ ₁₂

(в центре), σ22 (справа): десятичный логарифм от абсолютной разности точного решения (1) и приближенного решения (2), отнесенных к приложенной нагрузке σ∞

Fig. 1. The fields of absolute errors allowed by the truncation of the series on the 11th term for α=π/2 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂ (right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related to the applied load σ^∞

σ ₁₁                                     σ ₁₂                                     σ ₂₂

Рис. 2. Поля абсолютных погрешностей, допускаемых усечением ряда на 19-м слагаемом для α=π/2 и σ ₁₁ (слева), σ ₁₂ (в центре), σ ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения (1) и приближенного решения (2), отнесенных к приложенной нагрузке σ^∞

Fig. 2. The fields of absolute errors allowed by the truncation of the series on the 19th term for α=π/2 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂ (right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related to the applied load σ^∞

σ ₁₁

σ ₁₂

σ ₂₂

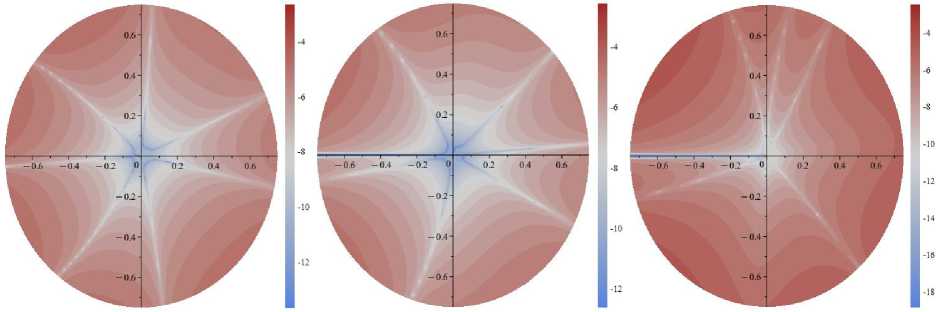
Рис. 3. Поля абсолютных погрешностей, допускаемых усечением ряда на 11-м слагаемом для α=3π/8 и σ ₁₁ (слева), σ ₁₂ (в центре), σ ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения ( 1 ) и приближенного решения ( 2 ), отнесенных к приложенной нагрузке σ^∞

Fig. 3. The fields of absolute errors allowed by the truncation of the series on the 11th term for α=3π/8 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂ (right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 )

related to the applied load σ^∞

^σ 11

^σ 12

^σ 22

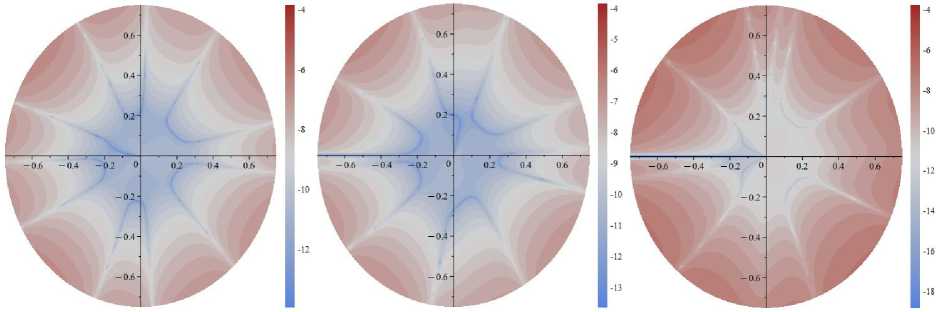
Рис. 4. Поля абсолютных погрешностей, допускаемых усечением ряда на 19-м слагаемом для α=3π/8 и σ ₁₁ (слева), σ ₁₂ (в центре), σ ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения ( 1 ) и приближенного решения ( 2 ), отнесенных к приложенной нагрузке σ^∞

Fig. 4. The fields of absolute errors allowed by the truncation of the series on the 19th term for α=3π/8 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂ (right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related to the applied load σ^∞

Для α=3π/8 абсолютная погрешность имеет примерно порядок 10 ^{- 12} для всех компонент напряжений, представляемых 11 слагаемыми ряда, и порядок 10 ^{- 13} для всех компонент напряжений, представляемых 19 слагаемыми ряда. Из рис. 1–8 можно выявить общие тенденции: 1) для каждой компоненты тензора напряжений имеются линии, где приближенное асимптотическое решение практически совпадает с точным решением, количество линий определяется числом членов асимптотического ряда, видом смешанного нагружения и

рассматриваемым материалом (ибо Т-напряжения в общем случае зависят от корней характеристического уравнения и, следовательно, от материальных свойств); 2) компонента тензора напряжения σ ₂₂ всегда проявляет меньшую погрешность (для всех типов комбинированного деформирования); 3) абсолютная погрешность для компонент σ ₁₁ и σ ₁₂ при уменьшении угла α также уменьшается, тогда как компонента σ ₂₂ оказывается менее чувствительной к виду смешанного нагружения, и значения абсолютной погрешности не меняются.

^σ 11

^σ 22

σ

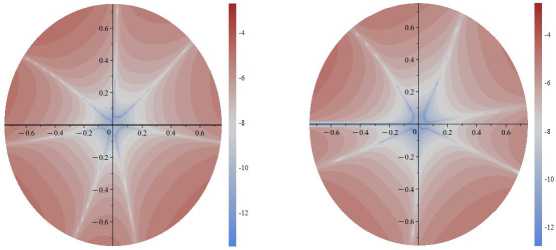
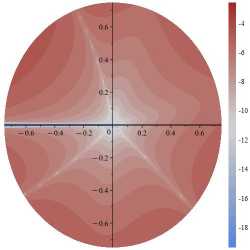
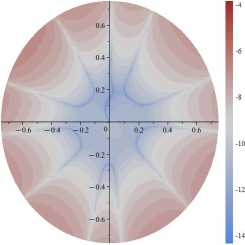
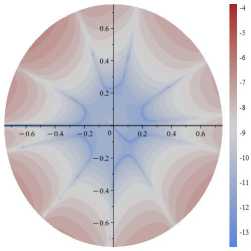
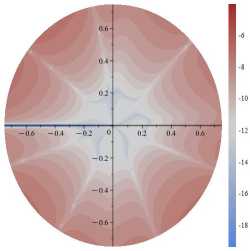
Рис. 5. Поля абсолютных погрешностей, допускаемых усечением ряда на 11-м слагаемом для α=π/4 и σ ₁₁ (слева), σ ₁₂ (в центре), σ ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения ( 1 ) и приближенного решения ( 2 ), отнесенных к приложенной нагрузке σ^∞

Fig. 5. The fields of absolute errors allowed by the truncation of the series on the 11th term for α=π/4 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂

(right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related

σ ₁₁

to the applied load σ^∞

σ ₂₂

σ

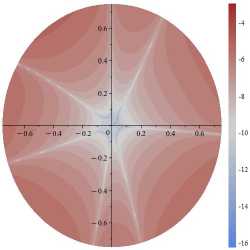
Рис. 6. Поля абсолютных погрешностей, допускаемых усечением ряда на 19-м слагаемом для α=π/4 и σ ₁₁ (слева), σ ₁₂ (в центре), σ ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения ( 1 ) и приближенного решения ( 2 ), отнесенных к приложенной нагрузке σ^∞

Fig. 6. The fields of absolute errors allowed by the truncation of the series on the 19th term for α=π/4 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂

(right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related

σ ₁₁

to the applied load σ^∞

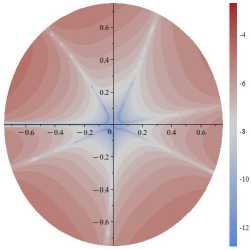
σ ₁₂

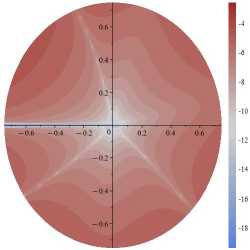
σ ₂₂

Рис. 7. Поля абсолютных погрешностей, допускаемых усечением ряда на 11-м слагаемом для α=π/8 и σ ₁₁ (слева), σ ₁₂ (в центре), σ ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения ( 1 ) и приближенного решения ( 2 ), отнесенных к приложенной нагрузке σ^∞

Fig. 7. The fields of absolute errors allowed by the truncation of the series on the 11th term for α=π/8 and σ ₁₁ (left), σ ₁₂ (center), σ ₂₂ right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related to the applied load σ^∞

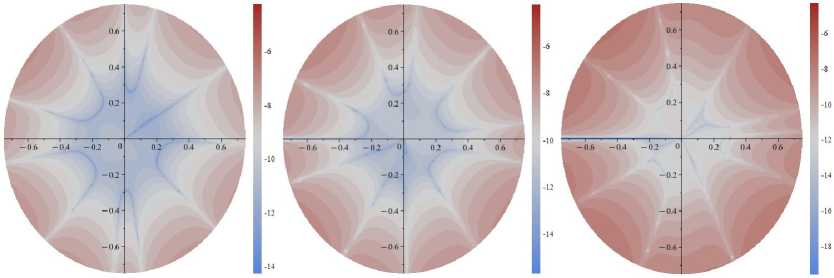
^ 11

^ 12

^ 22

Рис. 8. Поля абсолютных погрешностей, допускаемых усечением ряда на 19-м слагаемом для а = п /8 и G_n (слева), О ₁₂ (в центре), О ₂₂ (справа): десятичный логарифм от абсолютной разности точного решения ( 1 ) и приближенного решения ( 2 ), отнесенных к приложенной нагрузке о “

Fig. 8. The fields of absolute errors allowed by the truncation of the series on the 19th term for a = п /8 and G_n (left), G ₁₂ (center), C ₂₂ (right): Brigg’s logarithm (decadic logarithm) of the absolute difference between the exact solution ( 1 ) and the approximate solution ( 2 ) related to the applied load o “

Полученные поля абсолютных погрешностей дают возможность выбрать точки при их извлечении из опытных результатов измерений, осуществляемых, например, современными интерференционно-оптическими техниками (методами корреляции изображений, цифровой фотоупругости, спекл-интерферометрии) специальным образом. Из всего доступного экспериментального поля измеряемой величины следует выбирать те точки, в которых допускаемая абсолютная погрешность минимальна (т.е. точки, принадлежащие локусам точности), что позволит при последующей обработке и интерпретации результатов с более высокой точностью найти коэффициенты ряда ( 2 ) для напряжений и перемещений в опытных образцах с дефектами. Коэффициенты A_k , B_k многопараметрических рядов определяются в большинстве случаев путем переопределенного метода [10; 33; 34], который относится к техникам, требующим точных исходных данных, поэтому использование в качестве исходных точек, принадлежащих к локусам точности, приведет к уточненным оценкам коэффициентов рядов ( 2 ).

Оценка погрешностей, допускаемых усечением ряда

Для количественной оценки погрешностей, допускаемых при усечении асимптотического ряда (2) на N -м слагаемом, относительно точного аналитического решения (1), полученного на основании ТФКП, введем в рассмотрение L ₂ -норму:

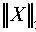
M

^ ( Xee^aci  XN asymP i=1

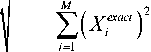
где X_i^Nasymp – физическая величина, оцениваемая с помощью асимптотического ряда, усеченного на N -м слагаемом, X_i^exact – значение величины, вычисленное посредством точного решения, базирующегося на ТФКП, M – количество точек, участвующих в разбиении отрезка [ -П , п ] .

Результаты вычислений относительной погрешности Е = || X ||2 • 100 %, проведенных согласно (3), для трех компонент тензора напряжений рассматриваемой плоской задачи на различном удалении от кончика трещины с учетом различного количества удерживаемых слагаемых в усеченном асимптотическом представлении приведены в табл. 1–15.

Из табл. 1–15 следует, что наибольшая погрешность наблюдается для нормальной компоненты напряжений а_п , очевидно, вследствие влияния Т -напряжений (табл. 1, 4, 7, 10, 13). В дополнение видно, что чем больше точка удалена от кончика трещины (чем больше зона, окружающая вершины трещины, требуется для изучения и анализа), тем больше слагаемых асимптотического ряда необходимо сохранять. Действительно, для значений углов a = п /2, в = 0 для расстояния r = 0,1 для достижения точности Е = 10 ^{- 5}% необходимо сохранить 11 слагаемых асимптотического ряда (первая строка табл. 1). Дополнительно, на основании проведенных расчетов, можно отметить, что для достижения погрешности, не превышающей Е = 10 ^{- 5}%, на расстоянии r = 0,6 для компоненты а_п необходимо рассмотреть 29 слагаемых асимптотического ряда. Для достижения погрешности, не превышающей 1 %, как это следует из данных табл. 1, на данном расстоянии, нужно сохранить семь слагаемых. Для достижения погрешности, не превышающей

e = 10 - 5 % , на расстоянии r = 0,6 для касательной компоненты о ₁₂ необходимо рассмотреть 31 слагаемое асимптотического ряда. Для достижения относительной погрешности, не превышающей 1 % на расстоянии r = 0,6, для компоненты а ₁₂ требуется девять слагаемых (последняя строка таблицы 2). Для достижения относительной погрешности, не превышающей 1 % на расстоянии r = 0,6, для касательной компоненты а ₂₂ требуется девять слагаемых (последняя строка табл. 3).

Из табл. 4, в которой приводится вычисленная относительная погрешность, допускаемая при различном количестве слагаемых ряда для а = п /2, в = п /12, следует, что даже для небольших расстояний от вершины трещины r = 0,2, для достижения относительной погрешности менее 1 % для компоненты тензора напряжений а_п необходимо удерживать пять слагаемых, тогда как

для расстояния r = 0,6 уже нужно сохранять девять слагаемых. В случае, когда требуется достичь погрешность, не превышающую Е = 10 - 5 %, для этой же компоненты нужно располагать 37-членным асимптотическим разложением на расстоянии r = 0,6 . При а = п /2, в = п /12 для компоненты тензора напряжений а ₁₂ на расстоянии r = 0,6 девятичленное асимптотическое разложение приводит к погрешности, не превышающей 1 %, однако если необходима более высокая точность, например, £ = 10 - 5 %, то следует сохранить 37 слагаемых. Для а = п /2, в = п /12 компонента тензора напряжений а ₂₂ на расстоянии r = 0,6 определяется семичленным асимптотическим разложением с погрешностью, не превышающей 1 % (табл. 6, последняя строка), однако, если необходима более высокая точность, например, Е = 10 - 5 %, то следует сохранить 33 слагаемых.

Таблица 1

Относительная погрешность, допускаемая для компоненты тензора ап на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Relative error for stress tensor component an at different distances with different numbers of retained terms of the series, %

Table 1

а = п /2 в = 0	N = 1	N = 2	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	122,90	19,004	0,4343	0,0149	0,00068	0,000037	0,20 - 10 - 5	0,11 - 10 - 6
r = 0,2	175,91	41,223	1,9039	0,1318	0,01194	0,00129	0,00014	0,00001
r = 0,3	192,37	58,629	4,1121	0,4307	0,05772	0,00927	0,00152	0,00025
r = 0,4	194,00	72,280	6,8553	0,9662	0,17060	0,03612	0,00792	0,00181
r = 0,5	191,31	84,324	10,1548	1,8071	0,39459	0,10337	0,10337	0,00824
r = 0,6	187,77	96,042	14,1176	3,0459	0,79067	0,24648	0,08181	0,02882

Таблица 2

Относительная погрешность, допускаемая для компоненты тензора а ₁₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Relative error for stress tensor component a ₁₂ at different distances with different numbers of retained terms of the series, %

Table 2

а = п /2 в = 0	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	6,330	0,349	0,0157	0,00070	0,00003	0,24 - 10 - 5	0,12 - 10 - 6
r = 0,2	11,59	1,370	0,1250	0,01141	0,00119	0,00013	0,00001
r = 0,3	15,92	3,051	0,4238	0,05865	0,00910	0,00152	0,00025
r = 0,4	19,44	5,420	1,0191	0,19012	0,03904	0,00858	0,00190
r = 0,5	22,26	8,560	2,0427	0,48140	0,12268	0,03331	0,00918
r = 0,6	24,51	12,626	3,6697	1,01784	0,31824	0,10257	0,03379

Таблица 3

Относительная погрешность, допускаемая для компоненты тензора а ₂₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 3

Relative error for stress tensor component a ₂₂ at different distances with different numbers of retained terms of the series, %

a = n /2 P = 0	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	4,49	0,092	0,0050	0,00025	0,00001	0,71 - 10 - 6	0,41 - 10 - 7
r = 0,2	8,47	0,338	0,0380	0,00394	0,00040	0,00004	0,51 - 10 - 5
r = 0,3	12,03	0,698	0,1227	0,01955	0,00306	0,00051	0,00087
Г = 0,4	15,24	1,142	0,2809	0,06102	0,01297	0,00289	0,00065
Г = 0,5	18,17	1,651	0,5347	0,14856	0,04007	0,01111	0,00315
r = 0,6	20,85	2,211	0,9092	0,31012	0,10175	0,03402	0,01144

Таблица 4

Относительная погрешность, допускаемая для компоненты тензора оп на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 4

Relative error for stress tensor component an at different distances with different numbers of retained terms of the series, %

a = n /2 в = п /12	N = 1	N = 2	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	126,09	21,819	0,5605	0,0214	0,00127	0,00009	0,20 - 10 - 5	0,11 - 10 - 6
Г = 0,2	178,78	47,411	2,4454	0,1844	0,02159	0,03146	0,00043	0,00005
r = 0,3	195,62	68,174	5,3034	0,5924	0,10304	0,02304	0,00481	0,00096
r = 0,4	198,17	85,260	8,9022	1,3128	0,30268	0,09238	0,02603	0,00689
r = 0,5	196,35	100,855	13,2557	2,4258	0,69992	0,27248	0,09670	0,03169
r = 0,6	193,45	116,231	18,4553	4,0341	1,40746	0,66909	0,28558	0,11103

Таблица 5

Относительная погрешность, допускаемая для компоненты тензора а ₁₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 5

Relative error for stress tensor component a ₁₂ at different distances with different numbers of retained terms of the series, %

a = n /2 в = п /12	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	7,237	0,465	0,0230	0,00112	0,00007	0,52 - 10 - 5	0,36 - 10 - 6
r = 0,2	13,17	1,839	0,1834	0,01773	0,00223	0,00003	0,00004
r = 0,3	18,00	4,129	0,6213	0,08936	0,01656	0,00368	0,00079
r = 0,4	21,93	7,405	1,4940	0,28474	0,06932	0,02082	0,00608
r = 0,5	25,19	11,821	2,9949	0,70985	0,21388	0,08135	0,30039
r = 0,6	28,06	17,637	5,3770	1,52288	0,54835	0,25354	0,11303

Таблица 6

Относительная погрешность, допускаемая для компоненты тензора а ₂₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 6

Relative error for stress tensor component a ₂₂ at different distances with different numbers of retained terms of the series, %

а = п /2 р = л /12	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	4,70	0,104	0,0073	0,00042	0,00002	0,15 - 10 - 5	0,11 - 10 - 6
r = 0,2	8,84	0,378	0,0568	0,00664	0,00072	0,00009	0,00001
r = 0,3	12,53	0,771	0,1867	0,03326	0,00547	0,00104	0,00022
r = 0,4	15,86	1,249	0,4342	0,10471	0,02298	0,00576	0,00165
r = 0,5	18,98	1,793	0,8392	0,25617	0,07030	0,02177	0,00792
r = 0,6	21,70	2,407	1,4461	0,53469	0,17593	0,06488	0,02850

Таблица 7

Относительная погрешность, допускаемая для компоненты тензора оп на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table7

Relative error for stress tensor component Gn at different distances with different numbers of retained terms of the series, %

a = n /2 в = n /6	N = 1	N = 2	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	58,39	15,618	0,48999	0,0320	0,00254	0,00020	0,00002	0,17 - 10 - 5
r = 0,2	88,10	35,277	2,12298	0,2928	0,04667	0,00714	0,00135	0,00025
r = 0,3	113,76	58,061	5,03417	1,1029	0,26257	0,05755	0,01703	0,00484
r = 0,4	137,50	83,367	9,28667	2,8743	0,90013	0,25293	0,10417	0,03934
r = 0,5	159,63	110,269	14,8708	6,0791	2,32583	0,79285	0,42592	0,19875
r = 0,6	179,72	137,406	21,6901	11,1655	4,96854	1,99522	1,33748	0,73460

Таблицы 7–9 показывают относительные погрешности для компонент тензора напряжений при a = n /2, в = n / 6. Из данных табл. 7 следует, что относительная погрешность для компоненты оп становится меньше, чем 1 %, на расстоянии r = 0,1, если удерживать три слагаемых; на расстоянии r = 0,3 для получения погрешности, меньшей 1 %, следует удерживать семь слагаемых, однако уже на расстоянии r = 0,6 необходимо прибегать к тринадцатичленному разложению. Если необходимо достичь большей точности, например, Е = 10-5%, то следует сохранить 57 слагаемых ряда для составляющей ап . Вычисляемая относительная погрешность для компоненты а12 становится менее 1 % на расстоянии /' = 0,1, если удерживать также три слагаемых, однако уже на расстоянии r = 0,6 необходимо прибегать к одиннадцатичленному разложению. Для представления касательного напряжения на расстоянии r = 0,1 с точностью Е = 10-5% необходимы тринадцать слагаемых. На том же расстоянии для нормальной компоненты а22 необходимы одиннадцать слагаемых. Одночленное разложение для компоненты а22 приводит к погрешности, равной 4 %, для касательной компоненты а12 одночленное разложение приводит к относительной погрешности более 6 %, а для ап погрешность составляет более 58 %, добавление Т-напряжений снижает погрешность до 15,62 %, тогда как добавление третьего слагаемого позволяет снизить погрешность на расстоянии r = 0,1 до 0,48 %.

Таблица 8

Относительная погрешность, допускаемая для компоненты тензора а ₁₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 8

Relative error for stress tensor component a ₁₂ at different distances with different numbers of retained terms of the series, %

а = п /2 в = п /6	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	6,495	0,399	0,0233	0,00177	0,00015	0,00001	0,12 - 10 — 5
r = 0,2	13,11	1,618	0,1801	0,02879	0,00508	0,00082	0,00015
r = 0,3	19,89	3,669	0,5868	0,14786	0,03931	0,00919	0,00270
r = 0,4	26,84	6,530	1,3403	0,47470	0,16727	0,05028	0,02036
r = 0,5	33,92	10,121	2,5181	1,17497	0,50904	0,18575	0,09736
r = 0,6	41,02	14,289	4,1795	2,45462	1,24370	0,53355	0,34743

Таблица 9

Относительная погрешность, допускаемая для компоненты тензора а ₂₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 9

Relative error for stress tensor component a ₂₂ at different distances with different numbers of retained terms of the series, %

a = n /2 в = п /6	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	4,08	0,085	0,0055	0,00035	0,00002	0,24 - 10 — 5	0,21 - 10 — 6
r = 0,2	7,76	0,321	0,0430	0,00532	0,00085	0,00015	0,00002
r = 0,3	11,11	0,687	0,1407	0,02536	0,00629	0,00176	0,00043
r = 0,4	14,18	1,698	0,3222	0,07541	0,02595	0,00974	0,00309
r = 0,5	17,00	1,759	0,6050	0,17330	0,07774	0,03614	0,01395
r = 0,6	19,62	2,452	0,9994	0,33832	0,18978	0,10388	0,04713

В табл. 10–12 приведены вычисленные относительные погрешности (%), допускаемые при усечении ряда для a = п/2, в = п/ 4. Из данных табл. 10 видно, что на дистанции /' = 0,1 асимптотический ряд с одним доминирующим слагаемым для компоненты ап приводит к относительной погрешности, равной 76,65 %. Добавление Т-напряжений дает возможность снизить погрешность до 21 %. Если располагать трехчленным асимптотическим разложением, то относительная ошибка не превышает 1 %. С увеличением расстояния количество сохраняемых слагаемых усеченного ряда для достижения требуемой точности необходимо увеличивать. Например, на расстоянии r = 0,5 для компоненты ап для достижения погрешности меньше 1 %, необходимо оперировать тринадцатичленным разложением. Если требуется определить данную компоненту с точностью до Е = 10-5% на расстоянии r = 0,6, то необходимо оперировать 81-членным разложением. Подобные закономерности имеют место и для остальных компонент тензора напряжений. Например, на расстоянии r = 0,4 для компоненты а12 к погрешности меньше 1 %, приводит семичленное асимптотическое разложение. Если требуется определить касательное напряжение с точностью до Е = 10-5% на расстоянии r = 0,6, то необходимо оперировать 75-членным рядом. Из данных табл. 12 следует, что наименее чувствительной к высшим приближениям является нормальная компонента а22. Тем не менее для достижения точности, равной Е = 10-5% на расстоянии r = 0,6, необходимо прибегать к сохранению 60 слагаемых ряда.

Таблица 10

Относительная погрешность, допускаемая для компоненты тензора оп на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table10

Relative error for stress tensor component Gn at different distances with different numbers of retained terms of the series, %

a = n /2 P = n /4	N = 1	N = 2	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	76,65	20,554	0,88967	0,06528	0,00595	0,00057	0,00005	0,61 - 10 - 5
r = 0,2	118,17	47,019	4,10833	0,59431	0,10937	0,02066	0,00432	0,00089
r = 0,3	151,38	76,271	10,0547	2,13816	0,59680	0,16672	0,05281	0,01616
r = 0,4	177,78	106,095	18,6938	5,19499	1,94942	0,71633	0,30485	0,12328
r = 0,5	198,00	134,813	29,6726	10,1079	4,76759	2,16318	1,15733	0,58028
r = 0,6	212,76	161,338	42,4703	17,0389	9,67271	5,20991	3,35804	2,00651

Таблица 11

Относительная погрешность, допускаемая для компоненты тензора а ₁₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 11

Relative error for stress tensor component a ₁₂ at different distances with different numbers of retained terms of the series, %

a = n /2 в = n /4	N = 1	N = 3	N = 5	N = 7	N = 9	N = 11	N = 13
r = 0,1	6,88	0,488	0,0391	0,00338	0,00033	0,00003	0,35 - 10 - 5
r = 0,2	13,63	1,914	0,3108	0,05291	0,01048	0,00208	0,00004
r = 0,3	20,22	4,203	1,0351	0,25947	0,07789	0,02296	0,00747
r = 0,4	26,61	7,276	2,4058	0,78978	0,31852	0,12378	0,05404
r = 0,5	32,77	11,053	4,5834	1,84876	0,93681	0,45057	0,24714
r = 0,6	38,69	15,464	7,6940	3,66402	2,23434	1,27857	0,84462

Таблица 12

Относительная погрешность, допускаемая для компоненты тензора о22 на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 12

Relative error for stress tensor component o22 at different distances with different numbers of retained terms of the series, %

a = n/2 в = n/4	N =1	N =3	N =5	N =7	N =9	N =11	N =13
r = 0,1	3,91	0,073	0,0037	0,00027	0,00002	0,24 - 10 - 5	0,25 - 10 - 6
r = 0,2	7,44	0,273	0,0279	0,00423	0,00073	0,00015	0,00003
r = 0,3	10,67	0,578	0,0889	0,02050	0,00524	0,00161	0,00049
r = 0,4	13,61	0,968	0,1989	0,06170	0,02072	0,00855	0,00344
r = 0,5	16,32	1,429	0,3668	0,14287	0,05911	0,03062	0,01529
r = 0,6	18,82	1,949	0,5995	0,28032	0,137162	0,08530	0,05082

В табл. 13–15 показаны относительные погрешности, допускаемые при усечении рядов, для a = n/2,в = п/3. Для расстояний Г' = 0,1 одночленное разложение определяет компоненту оп с относительной погрешностью, равной 126 %. Двучленное разложение приводит к уменьшению погрешности до 24,3 %. Если необходимо определить компоненту оп с погрешностью менее 1 % на указанном расстоянии, нужно сохранить три слагаемых ряда. На расстоянии r = 0,6 только тринадцатичленное разложение приводит к погрешности меньше 1 % для ан , одиннадцатичленное - для компоненты о|2, пятичленное - для компоненты о 22.

Таблица 13

Относительная погрешность, допускаемая для компоненты тензора оп на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Relative error for stress tensor component an at different distances with different numbers of retained terms of the series, %

Table13

a = n /2 в = n / 3	N = 1	N = 2	N = 3	N = 5	N = 7	N = 9	N = II	N = I3
r = 0,1	126,04	24,362	0,95885	0,05928	0,00466	0,00041	0,00003	0,32 - I0 - 5
r = 0,2	185,45	53,847	4,39925	0,51232	0,08180	0,01513	0,00248	0,00045
r = 0,3	205,89	77,110	9,75049	1,60596	0,39366	0,11284	0,02674	0,00729
r = 0,4	208,87	94,957	16,3944	3,39751	1,14916	0,44839	0,13645	0,05025
r = 0,5	206,87	110,420	24,1878	5,91929	2,61937	1,28668	0,47184	0,22186
r = 0,6	203,08	125,272	33,1082	9,20526	5,16164	3,02389	1,28560	0,74694

Таблица 14

Относительная погрешность, допускаемая для компоненты тензора о|2 на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 14

Relative error for stress tensor component aI2 at different distances with different numbers of retained terms of the series, %

a = n /2 в = n / 3	N = I	N = 3	N = 5	N = 7	N = 9	N = II	N = I3
r = 0,I	6,41	0,35	0,0321	0,00237	0,00020	0,00002	0,I6 - I0 - 5
r = 0,2	11,85	1,686	0,2599	0,03647	0,00614	0,00118	0,00002
r = 0,3	16,40	3,716	0,8875	0,17741	0,04515	0,01356	0,00347
r = 0,4	20,14	6,555	2,1287	0,53914	0,18640	0,07648	0,02493
r = 0,5	23,16	10,313	4,2076	1,26677	0,56427	0,29294	0,11575
r = 0,6	25,61	15,170	7,3582	2,53275	1,40932	0,87769	0,40385

Таблица 15

Относительная погрешность, допускаемая для компоненты тензора о ₂₂ на различных расстояниях с разным числом сохраняемых слагаемых ряда, %

Table 15

Relative error for stress tensor component о ₂₂ at different distances with different numbers of retained terms of the series, %

a = n /2 в = n / 3	N = I	N = 3	N = 5	N = 7	N = 9	N = II	N = I3
r = 0,I	4,04	0,075	0,0035	0,00024	0,00002	0,I4 - I0 - 5	0,I4 - I0 - 6
r = 0,2	7,69	0,282	0,0269	0,00372	0,00053	0,00009	0,00002
r = 0,3	10,99	0,590	0,0863	0,01863	0,00392	0,00098	0,00030
r = 0,4	13,99	0,980	0,1960	0,05222	0,01581	0,00532	0,00221
r = 0,5	16,74	1,435	0,3699	0,14004	0,04587	0,01960	0,01034
r = 0,6	19,28	1,943	0,6225	0,28463	0,10783	0,05667	0,03606

В [35] исследуется возможность экспериментального определения независящего от пути J -интеграла для полимеров с упругими и упругопластическими свойствами посредством метода корреляции цифровых изображений (digital image correlation, DIC). С целью вычисления инвариантного J -интеграла подробно обсуждаются необходимые аналитические концепции и подходы исследования образцов с односторонним надрезом на растяжение, изготовленных из полиметилметакрилата (ПММА) и полиэтилена, синтезируемого при низком давлении (ПНД), подвергаются испытаниям в условиях нагружения в чистом режиме I. С помощью DIC были испытаны три образца каждого материала при различных нагрузках с целью нахождения поля смещения на поверхности каждого образца. Далее с помощью метода наименьших квадратов найденное посредством DIC экспериментально поле смещения используется для определения сингулярных и неособых членов разложения Уильямса высшего порядка. Затем путем объединения этих слагаемых вычисляется J -интеграл для каждого образца. Кроме того, J -интеграл, полученный с помощью DIC, сравнивается с интегралом, полученным с помощью анализа конечных элементов, и наблюдается отличная корреляция. В статье [35] также обсуждается влияние различных параметров DIC на результаты расчетов. При анализе результатов экспериментов все точки, находящиеся на определенном радиальном расстоянии перед вершиной трещины, были сгруппированы вместе. Так, радиальное расстояние первой группы колеблется от 0 до 2 мм, второй группы – от 1 до 3 мм и так далее. После извлечения данных о перемещении из каждой группы (для перемещений вдоль горизонтальной и вертикальной осей) вычисляется J -интеграл. Авторы отмечают, что для ПММА в диапазоне радиальных расстояний от 0 до 2 мм погрешность составляет приблизительно 100 %. Оказывается, что увеличение расстояния от кончика трещины уменьшает ошибки. Для ПНД, как и для ПММА, наблюдается большое расхождение, когда данные выбираются близко к вершине трещины, в то время как при увеличении расстояния погрешность уменьшается. Более того, экспериментальные точки, расположенные на расстояниях, превышающих 2 и 3 мм, приводят к погрешности менее 8 и 5 % при вычислении J -интеграла для ПММА и ПНД соответственно.

В табл. 1–15 приведены ошибки вычислений, допускаемые при усечении слагаемых ряда, представляющего напряжения, именно на таких расстояниях, соответствующих экспериментальным измерениям, в рамках интерференционно-оптических методов и метода корреляции цифровых изображений.

Авторы заключают, что для обоих материалов N1 = 6 , где N1 – число удерживаемых слагаемых ряда Уильямса, достаточно, чтобы получить точные результаты для J-интеграла. В обоих случаях при выборе N1 = 6 расхождение между результатами конечно-элементного анализа и экспериментом составляет менее 8 % для ПММА и 5 % для ПНД, что свидетельствует о превосходной корреляции между ними. Стоит отметить, что N1 = 6 – это число неособых членов, включая сингулярный член первого порядка ряда Уильямса; таким образом, n1 = 6 соответствует N=11 членам, учитывая также сингулярные члены более высокого порядка. Это согласуется с результатами [36; 37], в которых сделан вывод, что чем дальше от вершины трещины получены смещения, тем больше слагаемых требуется для точного определения коэффициентов интенсивности напряжений для ПММА.

В [38] была предложена стратегия многопараметрической идентификации (определения коэффициентов многопараметрического разложения Уильямса), основанная на методе виртуальных перемещений, для выполненных тестов, которая позволяет одновременно характеризовать коэффициенты разложения с помощью одного эксперимента. Результаты [38] демонстрируют, что по мере увеличения радиуса рассматриваемой зоны идентифицированные значения масштабных множителей разложения Уильямса постепенно стабилизируются вокруг контрольных значений и относительные погрешности также постепенно уменьшаются и имеют тенденцию к стабилизации. Следует отметить, что в рассматриваемых образцах в рамках проведенного численного (конечно-элементного) моделирования рассматривалась пластина с одной боковой трещиной длиной 2 мм (ширина пластины составляла 6 мм), а исследуемые погрешности вычислялись на отрезке от 0 до 1,5 мм на продолжении линии трещины, т.е. r ˆ = 0,75 . Таким образом, расстояния, отраженные в табл. 1–15, в полной мере соответствуют реальным расстояниям от вершины трещины, на которых анализируются механические поля в ходе экспериментального или численного анализа.

Заключение

В работе приведен анализ напряженного состояния у вершины трещины в анизотропной среде с кубической сингонией упругих свойств. На основании 1) построенных угловых распределений напряжений на различном удалении от вершины трещины; 2) вычисленных полей абсолютных погрешностей между точным и приближенным решениями; 3) относительных погрешностей (3) компонент тензора напряжений разъяснен вклад регулярных слагаемых в общее представление поля напряжений. Рассмотрен общий случай, характеризующийся двумя углами, представляющих собой угол между ориентацией трещины и направлением действия растягивающей нагрузки и угол между направлением трещины и осью симметрии упругих свойств анизотропной среды соответственно. Вычислены десятичные логарифмы полей абсолютных погрешностей – разности точного и приближенного решений краевой задачи о растяжении ортотропной плоскости, ослабленной центральной наклонной трещиной. Продемонстрировано, что поля абсолютной погрешности обладают интересным свойством: присутствуют линии, вдоль которых наблюдается очень низкая погрешность и эти кривые можно интерпретировать как локусы точности, в которых приближенное решение полностью восстанавливает точное решение. Приведены относительные погрешности, допускаемые при усечении многокомпонентных разложений на N-м слагаемом ряда, по сравнению с точным аналитическим решением. Основная черта, свойственная асимптотическим разложениям полей напряжений, ассоциированным с вершиной трещины, состоит в том, что регулярные слагаемые становятся значимыми с увеличением расстояния от кончика трещины и позволяют существенно расширить область, где справедливо асимптотическое решение задачи. Присущей особенностью выполненного анализа угловых распределений напряжений