Эффекты увлечения и завихренности при ветровом прибрежном апвеллинге и даунвеллинге на примере юго-восточной части Балтийского моря

Процессы прибрежного апвеллинга и даунвеллинга характеризуются направленным приблизительно вдоль берега геострофическим течением, поперечным Экмановским переносом, адвективным переносом вод между различными слоями моря в присклоновой области. Одновременно с этим в достаточно широкой прибрежной части моря — с масштабом прядка радиуса деформации Россби — происходит характерное изменение термохалинной структуры. При апвелинге происходит увлечение относительно холодных вод из глубинных слоев на поверхность, а при да-унвелинге, наоборот, поверхностные воды из прибрежной части увлекаются в более глубокую, удаленную от берега часть моря.

Настоящая работа посвящена исследованию пространственно-временной структуры скоростей течений и изменчивости структуры термохалинных полей, возникающих при апвеллинге и даун-веллинге в юго-восточной Балтике. Исследования проводились на основе численного моделирования. Особое внимание уделено рассмотрению пространственной структуры потоков увлечения. Именно эти процессы приводят к изменению температуры в прибрежной части моря, а в верхнем слое к перестройке концентрации биогенных элементов. Приток и отток вод в поперечном к берегу направлении может также влиять на перемещения примесей и, в частности, на перемещение донных осадков в сторону открытого моря или, наоборот, к берегу.

• II.    Анализ ветрового воздействия в юго-восточной Балтике

  Анализ данных скорости ветра, полученных на прибрежных метеорологических станциях, расположенных вдоль побережья юго-восточной Балтики, показывает, что заметно преобладают ветра западных и юго-западных направлений [1]. Оценки влияния ветров на формирование явлений апвеллинга и даунвеллинга следует уточнить, используя данные измерений в открытом море. Были рассмотрены метеоданные, зарегистрированные на нефтедобывающей платформе Д-6, расположенной в море на расстоянии примерно 22 км от берега. На рис. 1 представлена гистограмма направлений скорости ветра за 2007 г. (данные для других годов, начиная с 2004 г. также были

рассмотрены). Данные предоставлены фирмой ЛУКОЙЛ «Калининграднефтегаз». В представленной на рис. 1 гистограмме учтены данные только тех скоростей ветра, амплитуда которых превышала 6 м/с. Это связано с тем, что при меньших скоростях ветра скорости течений в море слабо выражены. Амплитуда скорости ветра непосредственно не учитывалась. Рассматривались 8 секторов направления ветра, начиная с сектора 0 ° -45 ° и до 315 ° -360 ° . Именно такой выбор секторов направления скорости ветра дает более реалистичное представление об его влиянии на механизмы генерации апвеллинга и даунвелинга в юго-восточной Балтике.

Было получено, что ветра в секторе 0°-90° наблюдались 16,5 суток в году. Ветра в секторе 180°--270° отмечались почти в течение 42 суток в году. (Соответствующие значения для ветров, вызывающих апвеллинг и даунвеллинг, в 2006 г. были 19,4 и 68,3.) Таким образом, было получено, что вероятность события апвеллинга в юго-восточной Балтике почти в 2,5 раза меньше, чем даунвеллинга.

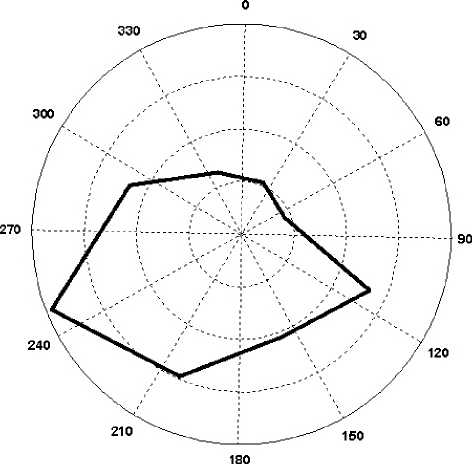
Рис. 1. Гистограмма направлений скорости ветра, большей 6 м/с, за 2007 г

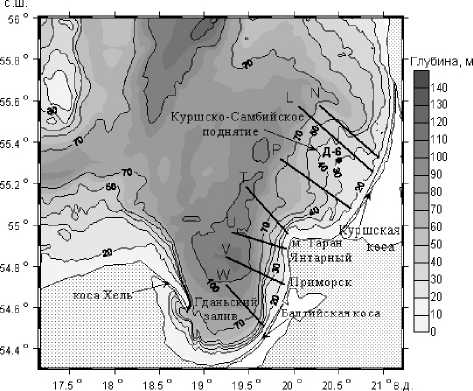
Рис. 2. Батиметрическая карта юго-восточной части Балтийского моря. Изображенная область является областью моделирования. Линиями N , L, P , T , U , V и W нанесены разрезы, на которых анализировались данные моделирования. Положение разреза натурных данных о термохалинной структуре апвеллинга в октябре 2005 г. совпадает с положением линии L. Кругом указано положение нефтедобывающей платформы Д-6

• III.    Гидродинамическая модель и ее обоснование на примере измерений апвеллинга

В настоящей работе при моделировании используется Принстонская модель океана (POM) [2]. Модель является трехмерной, гидростатической, по вертикали используется σ-координата, применяется расщепление на внешнюю (баротропную) и внутреннюю (бароклинную) моды. Для расчёта коэффициентов вертикального обмена импульсом, телом и солью модель содержит встроенную подмодель турбулентности с замыканием второго порядка типа Меллора–Ямады [3]. Считается, что эта турбулентная модель довольно реалистично воспроизводит динамику процессов вертикального перемешивания. Поэтому в настоящей работе предпринята попытка оценить вертикальную структуру турбулентной вязкости при апвеллинге и даунвеллинге.

Рассматриваемая область (рис. 2) имеет частично открытую западную и полностью открытую северную границы. На открытых границах было задано условие излучения [2, 4]. Пространственное разрешение в плоскости XY , заданное в модели, составляло около 1 км по долготе и широте. По вертикали было задано 36 слоев.

Модель была откалибрована по натурным данным о вертикальной структуре термохалинных полей с высоким пространственным разрешением [5]. Удалось весьма удовлетворительно воспро- извести структуру поля температуры на разрезе L, измеренную в 74-м рейсе НИС «Профессор Штокман» 17 октября 2005 г. во время апвеллинга (рис. 3(а) и 3(б)) [6]. В качестве начальных распределений по температуре (T) и солености (S) использовались данные на вертикальном профиле, полученном в юго-восточной Балтике в период спокойной погоды, предшествующий апвеллингу. Начальная стратификация полей T и S бралась однородной по горизонтали.

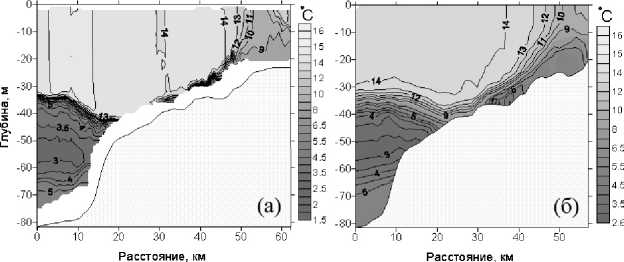
Рис. 3. Поля температуры T , полученные по данным натурных наблюдений в 74-м рейсе НИС «Профессор Штокман» 17.10.2005 г. на разрезе L(а) и по данным численного моделирования (б)

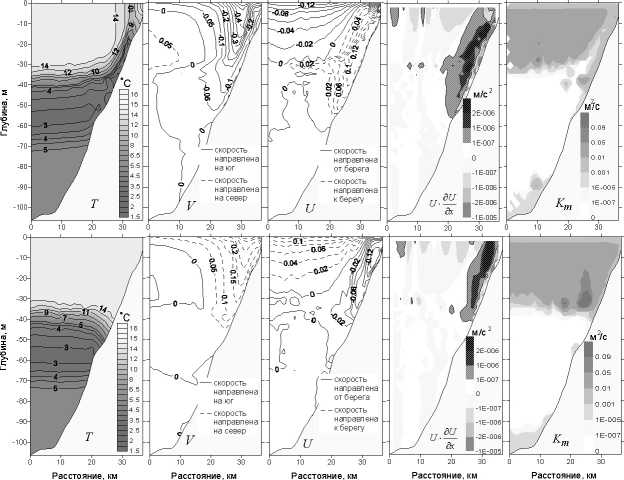
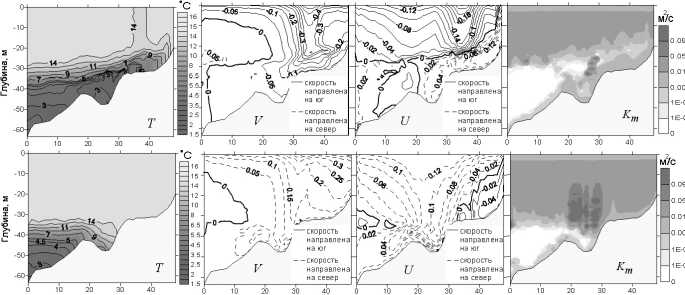
Рис. 4. Распределения температуры T , вдольбере-гового V (∆V = 0,05 м/с), поперечного к берегу U (∆U = 0,02 м/с) компонент скорости, адвективного члена U ^∂ _∂ ^U _x и коэффициента вертикальной турбулентной вязкости K _m для процессов апвеллинга (сверху) и даунвеллинга (снизу) на разрезе U. Результаты моделирования соответствуют 1 сут 20 ч

• IV.    Структура поля температуры вдольбереговых и поперечных к берегу течений на различных вертикальных разрезах

После того как результаты моделирования пространственной структуры поля температуры при апвеллинге подтвердили реалистичность прогноза, была исследована структура течений и термохалинные поля при апвеллинге и даунвеллинге во всей области моделирования. В определенном смысле динамическая природа этих двух процессов сходна. Оба эти процесса определяются квазигеострофическими течениями, экмановским и компенсационным переносами. Однако из-за сложной топографии дна и искривления береговой лини симметричное отображение течений в противоположные стороны не должно происходить (если конечно не рассматривать тривиальный случай однородного рельефа).

Был рассмотрен вопрос о том, как расходятся структуры течений, термохалинных полей и полей турбулентной вязкости для процессов апвеллинга и даунвеллинга. Эти поля анализировались на вертикальных разрезах, расположенных почти перпендикулярно береговой линии. Положения разрезов показаны на рис. 2. На рис. 4 и 5 представлены распределения температуры T , вдольберегового V , поперечного к берегу U компонент скорости и коэффициента вертикальной турбулентной вязкости K _m для процессов апвеллинга (сверху) и даунвеллинга (снизу) на разрезах U и N соответственно. Для разреза U также представлено распределение адвективного члена U ^∂ _∂ ^U _x в уравнении Навье–Стокса. Результаты моделирования соответствуют 1 сут 20 ч. Скорость ветра в течение 20 ч линейно нарастала до 12,5 м/с и в дальнейшем оставалась постоянной. Моделирование апвеллинга проводилось при ветровом воздействии северо-восточного направления, даунвеллинга — при ветровом воздействии западного направления.

Результаты моделирования поля T показывают степень распространения относительно холодных вод на поверхность моря при апвеллинге и поступление поверхностных вод открытого моря в более глубокие слои в прилегающей к склону области при даунвеллинге. Как правило, именно по данным T оценивается проявление апвеллинга и по данным T в вертикальной плоскости — проявление даунвеллинга. В динамических полях апвеллинг и даунвеллинг проявляются прежде всего в виде струйных вдольбереговых квазигеострофических течений в сложном поперечном переносе, связанном с Экмановским переносом и компенсационным течением. Структура квазигеострофического течения (V) на вертикальных разрезах характеризуется выраженными струями шириной примерно 6--8 км (то есть поперечный масштаб струй близок к радиусу деформации Россби, который в исследуемом районе по нашим оценкам составил примерно 4 км). Центр струи находится на удалении от берега в области с глубинами 32-- 35 м, то есть в области начала свала глубин и бровки шельфа. С увеличением глубины струя несколько смещается в сторону открытого моря.

Для разреза U пространственные структуры геострофических струй при апвеллинге и даун-веллинге близки. На разрезе N отмечается заметное различие геострофических струй. В случае даунвеллинга струя выглядит более размытой. Естественно предположить, что в случае апвеллинга геострофическая струя вторгается в рассматриваемую область из достаточно глубокой долины Пранемана (разрезе N расположен на краю этой долины). Во время даунвеллинга основное геострофическое течение поступает через Куршско–Самбийское поднятие, где оно расширяется и его интенсивность уменьшается.

Поперечные к берегу скорости течения (U) в несколько раз (примерно в 5 раз) меньше скоростей геострофических течений. В то же время авторы считают, что именно эти скорости определяют перенос вод между различными слоями, который возникает при апвеллинге или даунвеллинге. Рассмотрим структуру поперечной к берегу составляющей скорости течения на разрезе U . В поле поперечных к берегу течений в верхнем слое в мористой части разрезов хорошо обозначены изотахи, связанные с экмановским переносом в сторону открытого моря. В приповерхностном слое скорости соответствующих течений достигают 0,08-0,14 м/с. Нулевые значения устанавливаются на глубине 27-- 30 м. Для даунвеллинга эти величины имели примерно такие же значения, но объем самой структуры, внутри которой поперечная скорость была выше 0,08 м/с, оказалась несколько меньше.

В поле поперечной к берегу скорости на разрезе U, выделяется четко обозначенная структура в области склона, связанная с течениями, направленными к берегу при апвеллинге, и течениями, направленными в сторону открытого моря при даунвеллинге. При этом также отмечается узкая полоса в слое термоклина. Горизонтальная протяженность этой структуры около 10 км, а в области термоклина несколько больше, вертикальная протяженность составляет примерно 50 м. Авторы считают, что именно за счет этих составляющих скорости, сконцентрированных в присклоновой области, происходит перенос вод из относительно отдаленной от берега области моря в область склона, откуда происходит подъем глубоководных холодных и обогащенных питательными веществами вод на поверхность во время апвеллинга, а также перенос поверхностных вод из открытого моря в сторону берега, их опускание и, возможно, обогащение кислородом слоя термоклина при даунвеллинге.

Для даунвеллинга характерно более близкое расположение описанной структуры к поверхности моря по сравнению с апвеллингом. Формирование описанной структуры, прилегающей к склону, примерно в одной и той же пространственной области как при апвеллинге, так и при даун-веллинге, свидетельствует о том, что оба эти процесса весьма сходны по своей гидродинамической природе. При этом оба процесса являются локальными в том смысле, что геострофические струи и поперечные течения концентрируются в достаточно узком районе — шириной около 8-- 10 км, прилегающем к склону. Отметим, что вдольбереговые квазигеострофические струи и компенсационные течения накладываются друг на друга, но области максимальных скоростей не совпадают. Наибольшее расхождение в положении геострофической струи и поперечного течения отмечается на разрезе N в случае апвеллинга (рис. 5).

На примере разреза U была предпринята попытка установить природу компенсационного течения. Для этого совместно со скоростью течений и температурой были рассмотрены составляющие сил инерции в горизонтальном направлении UdU и WdU. На рассматриваемом разрезе наиболее выражена составляющая инерционного ускорения UQU (рис. 4). Ее структура близка к структуре поля скорости U. Область относительно высоких величин ускорений, направленных к берегу, порядка 10-7 м/с2 также сконцентрирована в области склона на горизонтальном масштабе около 10 км. Максимальные величины ускорений, направленных к берегу, составляют 2 • 10-6 м/с2. Эти распределения показывают, что именно горизонтальная сила инерции вызывает вовлечение воды из открытого моря в компенсационное течение во время апвеллинга и даунвеллинга. Более полное обоснование этого вывода было получено при сравнении адвективного члена U ∂∂Ux с другими членами уравнения движения (см. далее).

Расстояние, км                      Расстояние, км                 Расстояние, км                 Расстояние, км

Рис. 5. То же, что в рис. 4, но без адвективного члена для разреза N

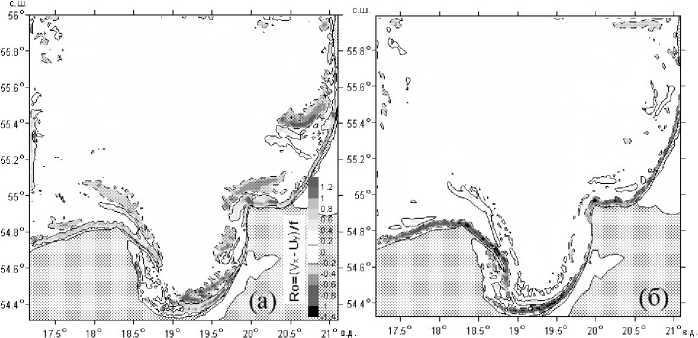
Рис. 6. Распределения локального числа Россби Ro = (V x — U y )/f , рассчитанные для горизонта 5 м по данным численного моделирования. Расчеты соответствуют северо-восточному (апвеллинго-вому) (а) и западному (даунвеллинговому) (б) ветрам продолжительностью 3 сут

• V.    Пространственные особенности распределения коэффициента турбулентной вязкости при апвеллинге и даунвеллинге

Особенности пространственной структуры интенсивности турбулентности в терминах вертикального коэффициента турбулентной вязкости K _m представлены в последних колонках на рис. 4 и 5. В целом эта структура характеризуется высокими значениями — порядка 10 ^{- 2} м ² /с — в верхнем слое. В термоклине значение K m спадает до 10 ^-3- 10 ^{- 5} м ² /с, а ниже термоклина снижается до уровня коэффициента молекулярной вязкости 10 ^{- 8} м ² /с. В придонном слое значение K m вновь возрастает примерно до 10 ^-4- 10 ^{- 5} м ² /с. Это соответствует фактическому увеличению турбулентных пульсаций в придонном погранслое. В прилегающих к склону областях, где наблюдается интенсивное увеличение поперечного течения U , при апвеллинге отмечаются выраженная область умеренной турбулентности с коэффициентом вязкости K m = 10 ^{- 3}-10 ^{- 5} м ² /с. Это в разной степени видно на всех рассмотренных разрезах (в том числе на рис. 4 и 5). Структура полей турбулентной вязкости во время даунвеллинга существенно другая. За счет опускания вод верхнего слоя в присклоновой области турбулентная энергия при даунвелинге распространяется на большие глубины. В верхнем слое на границе с термоклинном возникают замкнутые области, размер которых по горизонтали достигает 5-10 км и по вертикали около 10-15 м, в которых турбулентная вязкость K m доходит до 10 ^{- 1} м ² /с. Отметим, что точка Д-6 (см. рис. 2) находится вблизи отмеченной выше области с высоким уровнем турбулентной вязкости при даунвеллинге.

• VI.    Отличие горизонтальных структур завихренности (или числа Россби) при апвеллинге и даунвеллинге

Проводился анализ поля завихренности в области прибрежного апвеллинга. Для этого рас- считывались величины локального числа Россби Ro = o/f [7, 8], равного отношению локальной

∂V ∂U ∂x - ∂y

завихренности о =

к планетарной f . Физический смысл оценки числа Россби состоит в определении соотношения нелинейной центробежной силы и силы Кориолиса, которая опреде- ляет основной вклад в скорость геострофического течения. Из первого уравнения Навье–Стокса, написанного в виде [9]

dU₊udU ₊ 1 v fdV ₊ dU) + 1 w(dU + dWA ₊1 _w f^

dt dx 2 dx dy 2 dz dx 2 dx

1 dp

+ Km,

ρ ∂x∂z

∂W ∂x

1V dV - dU

2 dx dy

-

fV =

получается, что число Россби есть отношение ускорения вращения (ускорение, связанное с завихренностью) V (^ + ^d^U^ к ускорению силы Кориолиса fV . Поэтому не следует под ст понимать суммарный вклад всех инерционных сил U ·∇ U , входящих в уравнение Навье–Стокса, написанное в более традиционной форме:

^dU + ~ • vu + W^ - fV = - ∂t               ∂z

' £ ⁺ ^(Km ^ ⁺ F x . ρ 0 ∂x ∂z ∂z

При рассмотрении σ исключаются вклады U ∂∂Ux — ускорения линейной деформации, 2 V (dV + dU) + 2W (^ + dW) — ускорения угловой деформации (сдвига) и 2W (dUx — ^WW) — 2V (dV — d/) — ускорение вращения (вихревое). В рассматриваемой нами задаче это важно подчеркнуть, потому что выше и ниже специально рассматривается вклад члена U ∂∂Ux в формирование потока увлечения, связанного с неискривленной нелинейной адвекцией, не имеющего, подчеркиваем, отношения к числу Россби Ro. Это в значительной степени и предопределило необходимость рассмотрения этого параметра при исследовании процессов апвеллинга и даунвеллинга.

На рис. 6 (а) и 6(б) представлены распределения локального числа Россби Ro = ст/f , рассчитанного для горизонта 5 м по прошествии 3 сут модельного времени. На рисунке (а), относящемуся к апвеллингу, хорошо видны области относительно высокой локальной завихренности (Ro ~ 0,2-0,8). Здесь положительные значения Ro и ст соответствуют циклонической завихренности, а отрицательные — антициклонической. Циклоническая завихренность отмечается в прилегающей к берегу части струи, а антициклоническая — со стороны открытого моря. При этом циклоническая завихренность устанавливает тенденцию разворота квазигеострофической струи в сторону берега, а антициклоническая — в сторону открытого моря.

Несколько иная структура завихренности отмечается для даунвеллинга (рис. 6(б)). Знаки завихренности поменялись местами — в областях, где отмечалась циклоническая звихренность, она стала антициклонической и наоборот. Но главная особенность — это уменьшение значений локальной завихренности. В тех же самых областях она стала заметно ниже — модуль числа Россби находится в пределах Ro ~ 0,2-0,4.

В частности, в районе Куршско–Самбийского поднятия завихренность в терминах числа Россби уменьшилась от ~ 0,4 при апвелинге до ~ 0,1 при даунвеллинге. Незначительное уменьшение завихренности наблюдается только в отдельных районах: вблизи побережья косы Хель, вблизи северного побережья Самбийского полуострова. В более открытых частях моря завихренность при даунвеллинге мала.

• VII.    Оценка значимости нелинейной адвекции в области увлечения при апвеллинге и даунвеллинге

Важный (возможно и основной) вопрос при исследовании динамики вод при апвеллинге и да-унвеллинге состоит в том, чтобы установить, какова природа сил, вызывающих увлечение более плотных вод из глубинных слоев вверх (по наклонной плоскости) при апвеллинге, и увлечение поверхностных вод вглубь при даунвеллинге. Структуру увлечения естественно связать со структурой поперечной скорости U. При этом сама структура априори не ясна. В настоящей работе параметры этой структуры были установлены и описаны выше. В частности, было установлено, что направленные в сторону берега течения образуют вблизи склона компактную область. Именно в ней происходит увлечение.

Если рассмотреть процесс увлечения в терминах сил, то представляется важным оценить ускорение U ^∂ _∂ ^U _x , определяющее нелинейную адвекцию, и сопоставить его с другими членами уравнения движения (1): с ускорением силы Кориолиса, с ускорениями, связанным с завихренностью и турбулентной вязкостью. Оценки этих соотношений были выполнены для разреза U (см. рис. 2) и представлены на рис. 7.

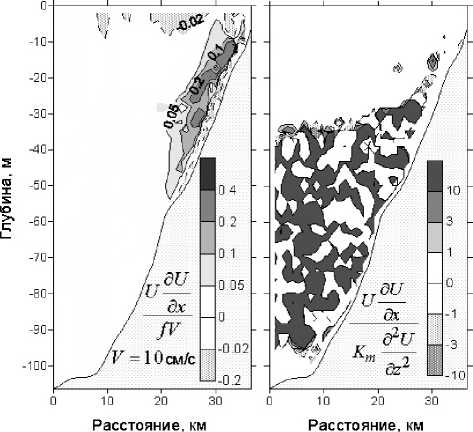
Рис. 7. Отношения инерционной составляющей ускорения U dU к ускорению силы Кориолиса fV (слева), при этом составляющая скорости V была положена равной 10 см/с, и ускорению, связанному с вертикальной турбулентной вязкостью K m^ZU (справа)

U ^∂U

Отношение f∂Vx имеет физический смысл в области, где состояние жидкости близко к геострофическому балансу (fV = — p^p) и где член UdU также существенен (см. рис. 4, 5). Для того чтобы сгладить структуру рассматриваемого соотношения в остальной части разреза и выделить только ту область, где рассматриваемые члены активно взаимодействуют, составляющая скорости V была положена равной 10 см/с. В области компенсационного течения рассматриваемое соотношение может достигать 0,2. Это означает, что член U|U вносит немалый вклад в баланс сил.

Рассмотрим отношение ускорения линейной деформации U |U к ускорению, связанному с тур-

U ∂U

булентной вязкостью: ^∂x . Значение этого соотношения постоянно меняется и довольно часто K _m ∂ U

∂z ²

находится в пределах от 3 до 10. Четкой структуры не наблюдается.

В области разреза U на глубинах 10-40 м число Россби Ro =

V ( ^dV - ^dU А ∂x ∂y

V(^ + 9U А ∂x ∂y

fV

мало и составляет око-

ло 0-0,2. Это означает также, что мал член   jV— (сдвиг), которая возникает в паре с завихренностью.

, характеризующий угловую деформацию

Слагаемое ^∂ _∂ ^U _t мало, 1 w с du + dW ) и i w с ди 2 ∂z ∂x 2 ∂z выраженной структуры.

-

поскольку рассматривается установившийся режим. Слагаемые

^∂ _∂ ^W _x также малы в области компенсационного течения и не имеют

Заключение

Структура течений и термохалинных полей при апвелинге и даунвелинге характеризуются как близкими особенностями, так и заметными различиями. Эти сходства и различия заключаются в следующем.

• 1.    В широких прилегающих к берегу областях моря на поперечных вертикальных разрезах структуры вдольбереговых квазигеострофических течений и поперечных к берегу течений, в том числе прилегающих к склону, весьма сходны. В общей структуре поперечных течений выделяется область с резким увеличением скорости до ~ 0,8 — 0,14 м/с. Эта область характеризуется горизонтальным масштабом ≈ 10 км и вертикальным масштабом ≈ 40 м. Авторы считают, что именно в этой области происходит вовлечение вод из глубинных слоев на поверхность при апвеллинге и, наоборот, — от поверхности в глубинные слоя — при даунвеллинге. Существенную роль при во-

• влечении играет горизонтальная нелинейная адвекция, выраженная в уравнении Навье–Стокса членом U dU. Близкое совпадение динамических структур апвеллинга и даунвеллинга нарушается в областях с резкой изменчивостью рельефа дна, например, в области Куршско–Самбийского поднятия и в области подводной долины Пранемана.

• 2.    Отмечается заметное различие модельной пространственной структуры турбулентности и ее интенсивности при апвеллинге и даунвеллинге. При апвеллинге наблюдаются более низкие, а при даунвеллинге — более высокие по сравнению с фоновым уровни коэффициента турбулентной вязкости в верхнем слое в области, примыкающей к склону. Для южной части Балтийского моря это район склона с глубинами ≈ 15--35 м. В районе со сложным рельефом, например в области долины Пранемана, при даунвеллинге в верхнем слое отмечаются перемежающиеся фрагменты горизонтальной протяженностью до 10 км, где уровень турбулентности может быть особенно высоким — соответствующий коэффициент турбулентной вязкости достигает 10 -1 м ² /с.

• 3.    Интенсивность и структура полей завихренности в горизонтальной плоскости при апвеллинге и даунвеллинге достаточно явно различаются. Завихренность при даунвелинге заметно меньше. Различие особенно выражено в отдаленной от берега части геострофической струи. Причина более высокой завихренности при апвеллинге может быть связана с ответвлением от основной струи вторичных струй — филаментов.

Работа выполнена при поддержке гранта РФФИ 10-05-00685.