Эйнштейн и Фреттинг. Булгаков и квантовая механика. Часть 1

рочность некоторых объемных материалов зависит от размера образующих их зерен. Математически эта закономерность выражается в виде формулы, получившей название закона Холла–Петча, согласно которой твердость материала Н возрастает при уменьшении размеров частиц по формуле:

h(d) = ho+A ,

где D — размер зерна, Но — твердость тела зерна, k — коэффициент пропорциональности.

Цель настоящей работы — определение подходов к управлению фреттингом.

Постановка задач:

• 1.    Анализ на феноменологическом уровне вопросов, связанных с возникновением неоднозначной связи между напряжениями и деформациями.

• 2.    Создание трибофизических моделей для определения физикомеханических характеристик наноматериалов.

ЭЙНШТЕЙН И ФРЕТТИНГ

«...Квантовая механика, конечно, впечатляет. Однако внутренний голос подсказывает мне, что это еще не настоящая вещь! Теория говорит много, но по существу ничуть не приближает нас к тайне Господа. Я, во всяком случае, уверен, что Он не играет в кости...»

А. Эйнштейн [29].

«…Эйнштейн обнаружил ограниченность ньютоновских законов движения, которые основывались на абсолютной системе координат, предусматривающей существование неподвижного, или абсолютного пространства. Последнее условие, по его мнению, вовсе не было необходимым. Оно было искусственным, не связанным с измерением; более того, оно являлось недостаточным теории, чем-то инородным, ненужным, усложненным. Он полагал, что этот недостаток вполне устраним. Следует найти такие законы, которые позволят наблюдателю судить о движении из любого наблюдательного пункта, любой системы отсчета…» [16].

«…Фреттинг-процесс – разрушение поверхностей трения деталей машин, проявляющееся в резко интенсифицированном (динамическом) окислении и схватывании. Происходит при трении скольжения с очень малыми колебаниями и приложении динамической нагрузки…» [34].

Влияние изменения свойств и состояния наноматериалов во времени на работоспособность прецизионных машин

«…Упругость является результатом статического сопротивления межатомных связей, вызываемого смещением атомов; во время деформации связи не нарушаются и работа деформации переходит либо в потенциальную энергию, либо в свободную энергию при понижении энтропии…».

«…При пластической деформации атомные связи разрываются, а затем снова восстанавливаются…» [20].

Класс точности и надежности машин и приборов во многом определяется несовершенствами упругости материала [33].

Максимальное сохранение во времени работоспособности и надежности автоматических станочных линий и систем могут быть обеспечены только при условии корректной оценки изменения свойств и состояния материала в функции времени [32].

Классическим примером статических законов может быть закон Гука (1), описывающий прямую пропорциональную зависимость между относительными удлинениями (деформациями) и нормальными напряжениями в идеальном однородном твердом теле:

о

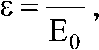
где ε – относительное удлинение, σ – напряжение, Е₀ – модуль упругости при σ = 0.

Иенш [28] предложил более точную зависимость n,a2

= — + —— о E

п,су3

E3

,

где n1 – коэффициент, равный для стали от 5 до 7.

Интенсивный рост упругого последействия начинается после перехода напряжений за 10% предела пропорциональности.

Согласно утверждению Н.Н. Давиденкова несоблюдение линейного закона характерно не только для таких много кристаллических агрегатов, какими являются технические металлы, но и для одиночных кристаллов. В реальных кристаллах соблюдение полного соответствия между напряжением и деформацией может быть нарушено при определённых обстоятельствах еще до начала пластического течения.

Поведение кристалла в этом случае называют неупругим [7]. Величина упругой деформации зависит не только от величины действующего напряжения, но и от времени воздействия напряжения.

Упругое последействие в отличие от ползучести относится к медленно обратимым процессам.

Упругое последействие без ползучести наблюдается в телах, напряженное состояние которых нигде не превосходит предела упругости.

Строго говоря, термин «упругое последействие» относится только к нагрузкам, не вызывающим перехода за предел упругости, иначе будет наблюдаться пластическое последействие [6].

Явлению последействия в твердом теле посвящена обстоятельная работа А.П. Бронского [3]. Не давая новой теории, А.П. Бронский показал, что физические положения для построения общей теории были даны Л. Больцманом и затем получили строгое математическое обоснование в работах Э. Вольтера.

Г.С. ИВАСЫШИН Энштейн и фреттинг. Булгаков и квантовая механика

В основе многих теорий последействия лежит представление о твердом теле как о совокупности идеальных упругих элементов с вязкопластическими.

При построении других теорий исходят из представления о кристаллическом строении твердого тела или же из предположения, что решающим фактором в явлении последействия является внутреннее трение.

Упругий гистерезис является следствием упругого последействия. Упругое последействие изменяет ширину петли гистерезиса.

Физическую картину возникновения неоднозначной связи между напряжениями и деформациями можно объяснить, применяя теорию дислокаций [41].

При прямом упругом последействии дислокации (местные искажения структуры) двигаются в направлении приложения нагрузки. При обратном упругом последействии дислокации стремятся вернуться в исходное положение.

Движение дислокаций происходит при напряжениях, более чем на два порядка меньших условного макроскопического предела текучести.

«…Движению дислокаций препятствует не только прочность разрываемых межатомных связей, но и рассеяние фононов и электронов проводимости в упруго искаженной области кристалла, окружающей движущиеся дислокации…» [43].

«…Энергия колебаний кристаллической решётки или энергия упругой волны является квантовой величиной. Квант энергии упругой волны назван фононом по аналогии с квантом электромагнитной волны – фотоном. Звуковые (упругие) волны в кристаллах – это распространение фононов…» [19].

Согласно С.О. Цобкалло, отличие упругого последействия от ползучести заключается только в величинах деформации и степени ее обратимости при разгрузке [45].

Анализируя погрешности упругих чувствительных элементов, Д.А. Браславский, С.С. Логунов, Д.С. Пельпор приходят к выводу, что упругое последействие и гистерезис – это явления, вызываемые внутренним трением в материале, из которого изготовлены элементы [2].

Упругое последействие оказывает влияние на величину рассеивания энергии при колебаниях, а также величину декремента затухания свободных колебаний. Эти вопросы, в частности, анализировал

Д.Ю. Панов, рассматривая применение теории упругого последействия к исследованию упругих колебаний при наличии гистерезиса [30]. Описывая широкие возможности метода внутреннего трения, М.А. Криш-тал, С.А. Головин отмечают в частности, применение метода внутреннего трения для оценки упругого последействия [17].

Упругое последействие материала приводит к процессам, развивающимся во времени – изнашиванию, фреттингу, коррозии, усталости металлов и т.д.

Под влиянием упругого последействия изменяется устойчивость во времени. Эти процессы изменяют работоспособность прецизионных машин [8–14, 22–27, 35–40].

Формула изобретения «Способ определениякоэффициента Пуассона» [36]

«Способ определения коэффициента Пуассона материала, заключающийся в том, что образец материала нагружают для создания одноосного напряжения и одновременно измеряют его продольные и поперечные деформации с помощью датчиков деформации, подключаемых к двум измерительным каналам регистрирующего устройства, меняют местами измерительные каналы с подключенными к ним датчикам, повторяют измерения и по среднему геометрическому результату измерений судят о коэффициенте Пуассона материала, отличающийся тем, что, с целью повышения точности измерений, измерение проводят при упругом последействии материала образца».

Формула изобретения «Способ определения модуляупругости материала» [37]

«Способ определения модуля упругости материала, заключающийся в том, что консольно закрепленную балку из испытуемого материала нагружают статически сосредоточенным усилием, приложенным к ее свободному концу, измеряют усилие и прогиб балки и по ним определяют модуль упругости материала, отличающийся тем, что, с целью повышения точности определения в условиях последействия материала, балку разгружают, измеряют изменение во времени остаточного прогиба и с учетом его определяют модуль упругости».

Формула изобретения «Способ определения модулясдвига образцов материала» [38]

«Способ определения модуля сдвига образцов материалов, заключающийся в том, что на образце в виде цилиндрического стержня отмечают кольцевыми рисками рабочий участок и образующую, замеряют длину l в образующей на рабочем участке, закручивают образец, разгружают его и замеряют величину крутящего момента µ_к и угол ϕ закручивания на рабочем участке, по которым судят о модуле упругости, отличающийся тем, что, с целью повышения точности определения, после разгрузки замеряют длины l₁ и L₁ образующей и кольцевых рисок и остаточный угол Δϕ закручивания, а модуль сдвига G и несовершенство модуля сдвига Δ G рассчитывают по формулам:

g =——

(ф-Аф)1р

AG = 64к Цк41 ,

(ф-Аф)^

где Jp – полярный момент инерции».

На основе научного открытия «Закономерность аддитивности упругого последействия в объемных частях и поверхностных слоях пар трения» (Диплом № 258) [22] разработаны оригинальные технические решения:

• •    «Способ определения коэффициента Пуассона» [36];

• •    «Способ определения модуля упругости материала» [37];

• •    «Способ определения модуля сдвига образцов материала» [38].

Формула изобретения «Способ определениядинамической твердости» [39]

«Способ определения динамической твердости, заключающийся в том, что воздействуют нагрузкой через индентор на испытуемый образец, определяют степень деформации образца и по ней судят о твердости, отличающийся тем, что, с целью расширения номенклатуры испытуемых материалов, мгновенно снимают нагрузку, измеряют де- формацию, обусловленную обратным упругим последействием, а твердость определяют по формуле

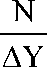
где N – нагрузка, Δ Y – обратное упругое последействие».

Формула изобретения «Способ оценки относительной износостойкости металлов» [40]

«Способ оценки относительной износостойкости металлов, заключающийся в том, что определяют твердость металла и пропорционально ей оценивают относительную износостойкость металла, отличающийся тем, что, с целью повышения точности за счет учета динамических эффектов, в качестве твердости определяют динамическую твердость».

Способ реализуется следующим образом (рис. 1). Образец-индентор 1, изготовленный из твердого материала и имеющий гладкую (полированную) рабочую поверхность, устанавливают на рабочую поверхность образца 2, (схема а), обладающую некоторой шероховатостью (схема б). На образец-индентор 1 воздействуют силой N, осуществляя тем самым его сближение с образцом 2, величина которого регистрируется с помощью автоколлиматоров 3 и зеркал 4, связанных с образцом-индентором 1.

Кривая ОВ (схема в) представляет собой первичное сближение образца-индентора 1 с образцом 2 из закаленной стали 40Х. Разгрузка от силы N сопровождается быстрым упругим возвратом величиной ω (отрезок СС₁) и упругим последействием величиной Δ Y (отрезок О₁С₁).

При повторном приложении нагрузки N соответствующий график сближения состоит из быстрого упругого сближения (отрезок О₁В₁) и медленного упругого последействия (отрезок В₁В. Регистрируя величину Δ Y последней составляющей сближения при повторном нагруже

N нии (схема г), можно рассчитывать динамическую твердость HI =--

AY и оценить относительную износостойкость ε материала образца 2 согласно зависимости

£ = CHI , где С – постоянная: С = 13,8•10–3 мм2/Н для отожженной стали.

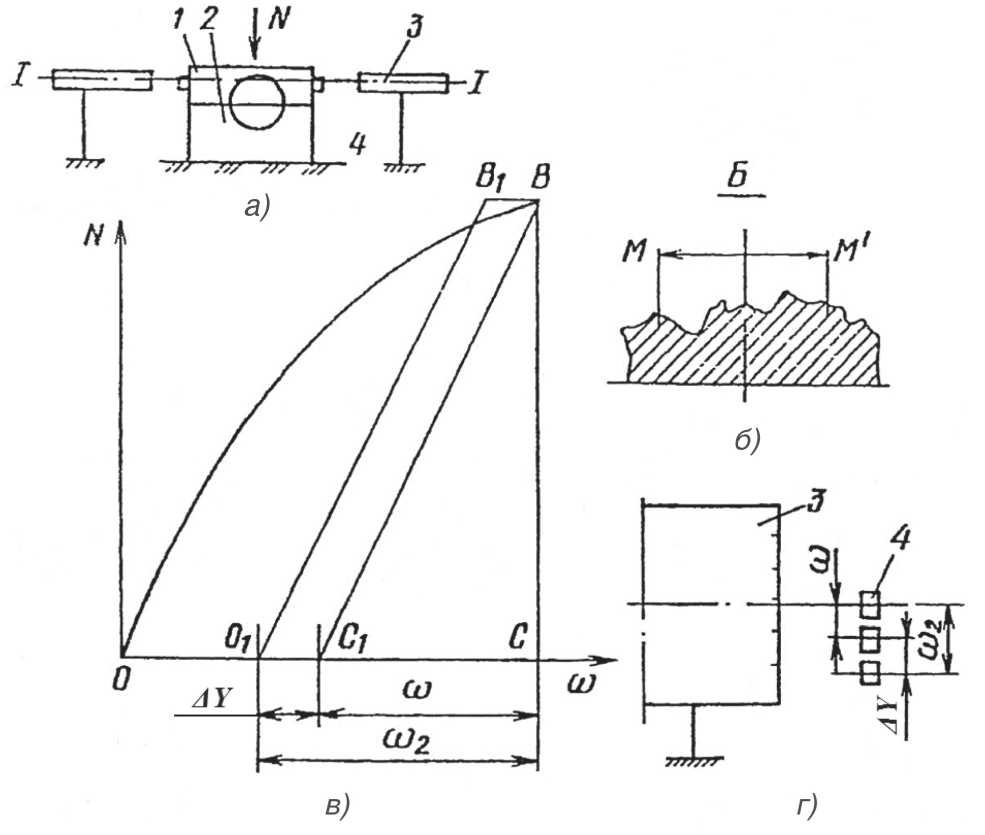
Рис. 1. Конструктивная схема экспериментальной установки и геометрия контактной задачи:

а) схема экспериментальной установки для определения упругого последействия;

б) рабочая поверхность исследуемого образца на длине ММ’; в) интерпретация зависимости упругого последействия от характера силового воздействия; г) регистрация упругого последействия относительно оптической оси автоколлиматора

Пример. Исследовалась износостойкость углеродистых и конструкционных углеродистых сталей. В табл. 1 и 2 представлены результаты испытаний, свидетельствующие о корреляции величины упругого Δ Y последействия и износостойкости сталей.

На основе научного открытия «Закономерность аддитивности упругого последействия в объемных частях и поверхностных слоях пар трения» (Диплом № 258) [22] разработаны оригинальные технические решения:

• •    «Способ определения релаксации остаточных напряжений в деталях» [35];

• •    «Способ определения динамической твердости» [39];

• •    «Способ оценки относительной износостойкости металлов» [40].

Таблица 1

Показатели	Марка стали
	20	35	40	50
Δ Y, мкм Скорость износа, мкм/ч	0,35–0,16 1,6•10–3	0,16–0,08 8•10–4	0,08–0,04 4•10–4	0,04–0,02 2•10–4

Таблица 2

Показатели	Марка стали
	15 Г	20 Г	30 Г	50 Г
Δ Y, мкм Скорость износа, мкм/ч	0,16–0,08 8•10–4	0,08–0,04 4•10–4	0,04–0,02 2•10–4	0,02–0,01 10–4

Продолжение статьи Ивасышина Г.С. «Эйнштейн и фреттинг. Булгаков и квантовая механика. Часть 2» будет опубликовано в Ин-тернет-журнале «Нанотехнологии в строительстве» №6/2013.

Уважаемые коллеги!

При использовании материала данной статьи просим делать библиографическую ссылку на неё:

Ивасышин Г.С. Энштейн и фреттинг. Булгаков и квантовая ме-ханика//Нанотехнологии встроительстве: научный Интернет-журнал. – М.: ЦНТ «НаноСтроительство», 2013. – Том 5, № 5. – C. 54– 72. URL: (дата обращения: _____________).