Экологические вопросы контроля за эксплуатацией скважин подземных хранилищ газа

В работе [2] показано, что в скважинах с установившимся тепловым потоком выявление интервалов заколонных перетоков и определение направления перетока успешно решается методами термометрии и иногда шумометрии. В настоящее время основным методом выявления заколонных перетоков в скважинах является термометрия. В эксплуатационных скважинах, в которых происходит закачка или отбор газа, решение этой задачи затруднительно из-за того, что температура в скважине зависит от многих факторов и в первую очередь от тепловой инерционности пород. Многообразие факторов, влияющих на распределение температуры в скважине, существенно осложняет решение задач при контроле ПХГ. Поэтому для обеспечения достоверной интерпретации данных скважинной термометрии важным моментом является использование модельных термограмм.

Математическая модель включает конвек-тивно-кондуктивный перенос тепла в системе эксплуатационная скважина ПХГ - окружающие горные породы в процессе воздействия (закачка или отбор газа), а также после прекращения воздействия учитывает радиальную и вертикальную теплопроводность, конвективный перенос в стволе скважины и пласте, интервалы заколонного движения флюида и пластового движения подземных вод, литологию, конструкцию скважины.

Модель пласта. Допущения: однофазность; пренебрежение гравитационными слагаемыми; полное вскрытие пласта; отсутствует течение в вертикальном направлении. Описываемые процессы: нестационарность; конвективный перенос в радиальном направлении; кондуктивный перенос в радиальном и вертикальном направлениях; адиабатический эффект; эффект Джоуля-Томсона. Граничные условия: кондуктивный теплообмен на верхней и нижней границах; заданное давление на внутренней и внешней границах или заданное давление и расход на внутренней границе; заданная температура втекающей жидкости на внутренней и внешней границах; заданный кондуктивный тепловой поток на внутренней границе.

Уравнение сохранения массы:

d ( m p ) = 1 M _{r p} k d p ) d t r d r V ц d r J ’

R <  r <  R k

где μ – вязкость, р – давление, Rw, R k – радиусы скважины и контура питания, к- проницаемость.

В случае, если сжимаемостью пласта пре-небрегается, уравнение преобразуется к следующему виду:

p r = R w = ^Pw , p l = R = P k              (8)

где Pw, Pk – давление в скважине и на контуре питания.

Граничные условия на внутренней и внешней границе при сопряжении с моделью канала перетока:

p r = R w    P^ch , ^{D r} = R w   2 n R w ( H bOL - H_{t op} )        (9)

где Q ch , P ch – величина расхода и давление на внутренней границе.

Полный тепловой поток на внутренней границе определяется как:

1 d f k dp ^ I r r dr V ц dr J

= О, R w <  r <  R k

Скорость фильтрации определяется из закона Дарси:

u =

k 9 p ц d r

Уравнение сохранения энергии:

г ⁸T J ⁸ (

C--+--(ruT) = dt   r 9r

1 a f * a t ) a f * a t )     a p

=--1 ra — 1 +--1 a, — 1 + mn-- r dr V dr J  9z V   dz J      91

9 p

- ED — ⁺ q bh ’ H _to <  z <  H b_ot_tom

9 r                                (4)

_{c =} ^mPc ^{+ (1} - ^m ))F>_s^^c_Sk P c

*

^a r

где η, ε – адиабатический и Джоуля-Томсона коэффициенты, ρ sk , c sk – плотность и теплоемкость скелета пласта, H top , H bottom – кровля и подошва пласта.

Граничные условия на верхней и нижней границах:

. a t

A a z

= 0

z = H op

. a t A az

,

= 0

^z H botom

.

т а * ⁸ T pcuT — Ar — dr

= Pc^U\_r_ _R^T wall ' ww

-I r = R w

—

w a ⁽ z ^{) [ t}|

r = R w

—

^Tw ( ch ) ( ^z ) ]

где T wall – температура стенки скважины.

Температура стенки T wall определяется по правилу против потока. Коэффициент α = h / R w . На внешней границе задается температура:

T r = R. = ^Tk ⁽ z ⁾

где T k (z) – геотермическое распределение температуры/

Модель скважины. Допущения: однофаз-ность; сжимаемый флюид; средние по сечению параметры (одномерность); пренебрежение потерями на трение; пренебрежение гидростатикой. Учитываемые процессы: нестационарность; конвективный теплоперенос; кондуктивный тепло-перенос в вертикальном направлении; адиабатический эффект; кондуктивный теплообмен с окружающей средой; конвективный массообмен с перфорированными пластами и каналами заколонного перетока. Граничные условия: заданное давление на верхней границе; заданная температура на верхней границе в случае нагнетания в скважину; отсутствие массовых и тепловых потоков через нижнюю границу.

Уравнение неразрывности:

du

w dz

—

^q nR in

—

-*w Z Q», 6⁽z — Z chj) ^Rm j

,

0 <  z <  H wel

Связывание будет осуществено через ис-точниковые слагаемые, задаваемые в граничных ячейках. Граничные условия на внутренней и внешней границах при сопряжении с моделью скважины:

где R in – внутренний радиус колонны. Уравнение сохранения энергии:

6 T w , S U w T w 8 1      8 z

-1 Ah ⁵ T w ) _ Д I A w Д I p c d z V d z J

qT wal¹- - 1 E Q chj T chw ^{5 (} z — ^Z

CR.    CR. j

Для второго участка предполагается, что

L2L pc Rin T ex )n 81

p _ch = const L_x <  z <  L

Уравнение сохранения энергии:

где T w – температура в скважине, T ex – температура на внешней границе.

Граничные условия:

^{d T}ch ! S U ch T ch

8 1       8 z

8 z

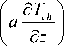
q ch T wau  8L2P h ex.

S ch     p c S ch

( T ch - T ex ) -

^U w l z = H = ⁰ P w = P h ^{( 1} ) T w l z = 0

,                                 ,

, d T w

^Aw^ О z

= 0

z = H wei

= Th (1)

,

±2 n h in P c ^Sch

( T ch - T w ) + n ^ P ch - a), d 1

^d P ch

8 z

Индексами in и ex обозначаются величины, относящиеся к внутренней и внешней стенкам канала соответственно. Граничные условия:

Модель канала перетока. Допущения: однофазность; сжимаемый флюид; средние по сечению параметры (одномерность); течение согласно закону Дарси; пренебрежение гидростатикой; пренебрежение градиентом давления в области, сопрягаемой с моделью пласта; равномерный профиль массообмена с пластом. Учитываемые процессы: нестационарность; конвективный теплоперенос; кондуктивный теплоперенос в вертикальном направлении; адиабатический эффект; эффект Джоуля-Томсона; кондуктивный теплообмен с горной породой, пластом и скважиной; конвективный массообмен с пластом и скважиной. Граничные условия: заданное давление на границе со скважиной; заданный массовый расход на границе со скважиной; заданная температура на границе со скважиной в случае нагнетания в канал перетока; отсутствие массовых и тепловых потоков через границу z = L 2 .

Модель заколонного перетока делится на два участка. Первый – от точки выхода в скважину до границы пласта-источника перетока (0≤ z ≤ L 1 ). Второй – в пределах пласта-источника перетока ( L 1 < z ≤ L 2 ). Уравнение неразрывности для первого участка:

^U ch\z = L = ^{0   U} ch\_z = 0

,

^T L - =0 = T h ^{( t} )

Q T , P l z = > ^{= P}h ⁽ 1 ) ,

Модель горной породы. Уравнение теплопроводности:

8Ts_{L =} d 1

1 d f      8 T_sk ) d f

- I r ^ask д I⁺ Д I ^ask r d r V     d r J  о z V

d T sk ) 6 z J

⁺ q bh

где T sk – температура горной породы, a sk – температуропроводность горной породы. При этом радиус внешней границы модели горной породы должен быть много больше, чем радиус температурного возмущения от скважины за моделируемый период. Граничные условия:

S Ts^

Ask  д оr

r = R k

I;   ^ T sp

= ⁰ I ^A sk  д

V      О r

,

^r = R w

h

_D V sk   w(c ( ch ) /

Rw

d = o „     , dz     0 < z < L

,

Для связанных с моделями пластов границ задается осутствие теплового потока, связывание реализуется через источниковые слагаемые. Для несвязанных также задается остутствие тепло-вого потока:

где υ ch – скорость в канале перетока.

Уравнение неразрывности для второго участка:

A sk

8 T

8z

z = H op

= 0

A sk

8 T

d z

= 0

z H bosom

duch _ Qch dz      Sch Lx < z < L 2

где S ch – поперечное сечение канала перетока, q ch = const – массообмен с пластом/

Уравнение движения для первого участка:

Замыкающие соотношения.

Параметры пласта и скважины. Пористость является линейной функцией давления:

^U ch

k ch ^d P ch ц 8 z

m = m 0 ⁺ P sk ⁽ P - ^P0 )

Здесь β sk определяется как

Psk =

где k ch – проницаемость канала перетока.

8 m d p

Теплопроводность насыщенной горной породы λ^* определяется по модели Лихтенеккера:

*     1-m m

Z - Ask Z

h ex = α channel R w – для теплообмена между потоком за колонной и горной породой.

Начальные и граничные условия. На границах

сред выполняются условия равенства температур

Параметры флюида. Плотность газа: ρ = P/zRT , где z – коэффиицент сверхсжимае-мости. Теплоемкость, теплопроводность, вязкость, коэффициент Джоуля-Томсона, адиабатический коэффициент считаются константами и определяются из соответствующих справочников.

Теплообменные коэффииценты. Коэффициенты теплообмена α вычисляются следующим образом:

^T i r — Ri

a , d ^ d r

^- 0    ^T i + 1\_r — Ri + 0

и тепловых потоков

r — R ,

^{— Z} i + 1 - 0

dT , + 1

6 r

.

r — R , + 0

A a — Nu —

D

Первоначальное распределение температуры в системе “скважина-пласт” геотермическое. Дискретизация уравнения переноса тепла проводится конечно-объемным методом, основываясь на регулярной сетке с переменными шагами. При r =0 ставится условие отсутствия потока тепла и массы. Шаги сетки по r неравномерные, выбира-

где Nu – число Нуссельта.

Гидравлический диаметр потока:

D — 4 S

P

,

где S – площадь сечения потока, P – периметр потока. Для скважины D =2 R , для потока за колонной D =2( R w – R c_ex ).

Коэффициент теплопередачи:

- между скважиной и горной породой (вне интервала НКТ)

ются исходя из геометрических размеров конструкции скважины и литологии. Размер шага и количество шагов сетки выбирается автоматически исходя из условия не менее 5 шагов сетки в каждой области конструкции скважины, при этом обеспечивается совпадение границ областей с какой-либо границей ячейки. В пласте и породах шаги сетки увеличиваются по мере удаления от оси скважины по квадратичному закону. Шаги сетки в вертикальном направлении также подбираются соответ-

ственно имеющимся границам пластов или конструктивных элементов. Конвективные слагаемые рассчитываются схемой против потока, диффузионные – центральные разности. Полученная система линейных уравнений решается методом переменных направлений.

h —

— + -Lh R w ^{a R} in    ^Z cem   ^Rex

- между скважиной и горной породой (в интервале НКТ);

h -------------------¹------------------

_{1      1     R}NKT    _{1     R}

--+ — ln — +--ln aRiN     Zan    Rin    Ze     Rex

- для теплообмена между потоком в скважине потоком за колонной (вне интервала НКТ)

in          1                 1

1 ^a well^Rin   Channel ^Rex

и

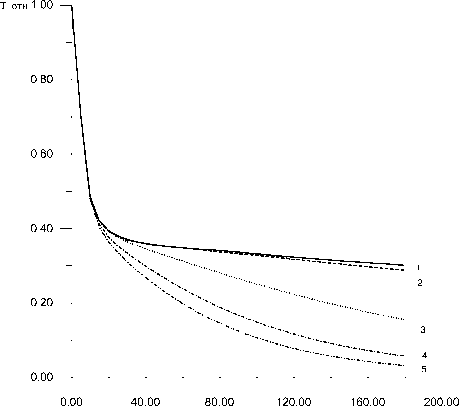
t,MUH

Рис. 1. Зависимость температуры от времени на глубине заколонного перетока газа с дебитами: 1 – 5, 2 – 50, 3 – 100, 4 – 500, 5 – 1000 тыс. м³/сут.

- для теплообмена между потоком в скважине потоком за колонной (в интервале НКТ);

и

hin

1ln awellRin   Zan

NKT

Rin

+ a. R channel ex

На рис. 1 приведены результаты расчетов зависимости температуры от времени в интервале заколонного перетока для различных дебитов заколонного перетока газа. Видно, что начиная с дебитов 200-500 м3/сутки температурное поле

чувствительно к изменению дебита заколонного перетока газа. Заколонный переток газа приводит к уменьшению скорости восстановления температуры в интервале перетока газа в скважине. Следовательно, измеряя кривую восстановления температуры в скважине через определенные промежутки времени, сравнивая ее с расчетной и геотермическим значением можно в эксплуатационных скважинах выявлять интервалы заколонных перетоков.

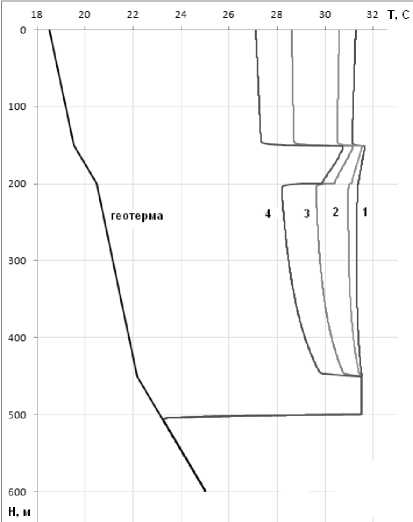
Рис. 2. Распределение температуры по глубине с дебитом заколонного перетока 500 м³/сут (при пластовых условиях): 1 – 0,5 часа, 2 – 1 час, 3 – 3 часа, 4 – 6 часов после окончания закачки

На рис. 2 приводится вариант расчета восстановления температуры по глубине при наличии заколонного перетока газа из продуктивного интервала в верхний пласт-коллектор после прекращения закачки газа. Данный пример соответствует случаю наличия солевой покрышки. Дебит заколонного перетока 500 м3/сут. Из рис. 2 видно, что после прекращения закачки газа наблюдается распределения температуры по глубине к геотермическому распределению температуры. Интервал, в который поступает газ за счет заколонного перетока, отмечается замедленным темпом восстановления температуры.

Сравнение распределения температуры при наличии заколонного перетока и без перетока приведено на рис. 3. Видно, что при наличии заколонного перетока (синяя кривая) в интервале заколонного перетока наблюдается замедленный темп восстановления температуры по сравнению со случаем без перетока. Изменение градиента температуры в этом случае (без перетока) связано только с литологией. А в интервале пласта – коллектора во всех случаях поглощения газа наблюдается отставание в темпах восстановления температуры.

Получение достоверной информации об интервалах и направлениях перетока газа выше резервуара ПХГ, при отсутствии явных признаков утечек из ствола, возможно при сравнительном анализе временных характеристик (например, кривых распределения температуры по разрезу, регистрируемых во времени по определенной технологии) с данными физического или математического моделирования и начальными фоновыми значениями. Начальные фоновые температурные характеристики снимаются перед пуском скважины в эксплуатацию, либо рассчитываются и реконструируются по результатам исследований наблюдательных и длительно простаивающих скважин.

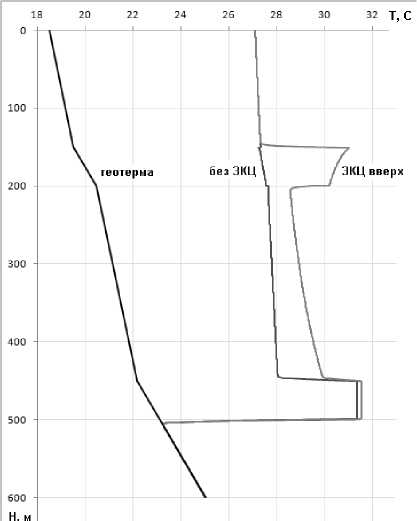
Рис. 3. Сравнение мгновенных распределений при наличии и отсутсвии ЗКЦ через 6 часов после окончания закачки

Получение достоверной информации об интервалах и направлениях перетока газа выше резервуара ПХГ, при отсутствии явных признаков утечек из ствола, возможно при сравнительном анализе временных характеристик (например, кривых распределения температуры по разрезу, регистрируемых во времени по определенной технологии) с данными физического или математического моделирования и начальными фоновыми значениями. Начальные фоновые температурные характеристики снимаются перед пуском скважины в эксплуатацию, либо рассчитываются и реконструируются по результатам исследований наблюдательных и длительно простаивающих скважин.

При выявлении скважин - источников техногенеза, совместная интерпретация предусматривает процедуру анализа совокупности отрицательных факторов, описанных выше, установлении природы температурных аномалий на кривых восстановления температуры выше резервуара хранилища, проведение математического моделирования с учетом геолого-технических условий каждой конкретной скважины и сопоставление теоретических кривых с реальными термограммами.

На рис. 4 приведены результаты термометрии скважины №1 одного из ПХГ и их сравнение с расчетными данными термограмм по стволу скважины. Промыслово-геофизические исследования были начаты с режима длительной закачки газа -кривая Тдин (рис. 2) и продолжены после остановки через 1, 5, 16 и 107 часов (кривые Т1ст, Т2ст, Т3ст и Т4ст). Расчетные кривые Т1мод, Т2мод, Тзмод приведены соответственно для 1, 5 и 16 часов с момента остановки скважины. Некоторое различие в распределении измеренной температуры Т1ст и модельной Т1мод связано влиянием конвективной составляющей (в математической модели считается, что после остановки скважины перенос тепла в стволе скважины происходит только за счет теплопроводности). Из рисунка видно, что в интервале 1130-1400 м на фоне условной геотермы на кривых Т1ст - Т4ст наблюдаются повышенные значения температуры по сравнению с аналогичными в интервале 400-1130 м. Указанные интервалы сложены каменной солью за исключением двух пропластков 1147-1200 и 1303-1321 м, где породы представлены переслаиванием глинисто-карбо-натных и сульфатизированных известняков и доломитов. Характер восстановления температуры в скважине для каменной соли должен быть одинаков на любой глубине. Замедление этого процесса в интервале 1200-1400 м, связано с наличием заколонного перетока газа вверх из резервуара хранилища в коллекторы, расположенные на глубинах 1147-1200 и 1303-1321 м, т.е. в глинисто-карбонатные известняки и доломиты филлипов-ского горизонта.

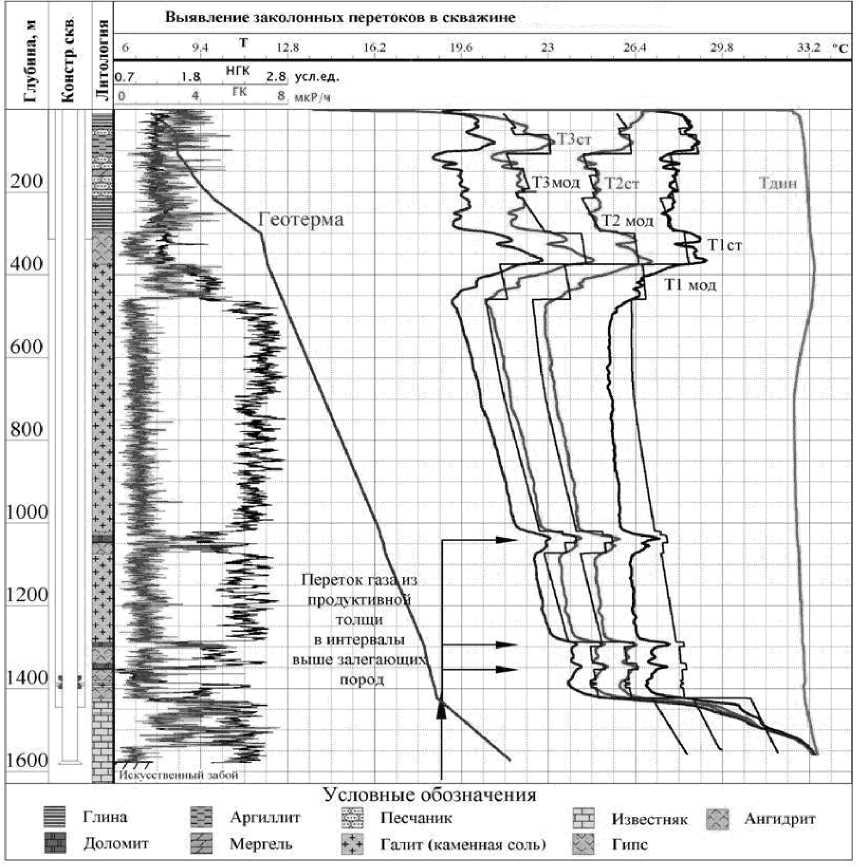
Рис. 4. Результаты промысловых исследований и сопоставление с результатами расчета

Выводы: математическое моделирование тепловых процессов в скважинах подземных хранилищ газа позволяет выяснить особенности распределения температуры в нестационарных условиях. Создание альбома кривых восстановления температуры для различных условий эксплуатации скважин ПХГ позволяет повысить уровень интерпретации по выявлению техногенных нарушений, определения работающих интервалов, заколонных перетоков и.т.д.