Экомониторинг воздушной среды города Зеленограда

Исследования проводились на основе статистических показателей загрязнения атмосферного воздуха, предоставленных территориальным органом Роспотребнадзора Зеленоградского АО и ГПБУ «Мосэкомониторинг» (таблица 1) на основании измерений постами экологического селитебных зонах.

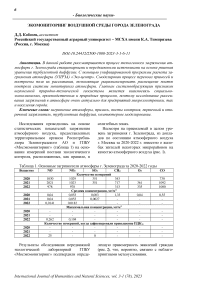
Несмотря на приемлемый в целом уровень загрязнения г. Зеленограда, из докладов по состоянию атмосферного воздуха г. Москвы за 2020-2022 г. известно о жалобах жителей некоторых микрорайонов на качество атмосферного воздуха (рис. 1).

контроля, расположенных, как правило, в

Таблица 1. Основные загрязнители атмосферы г. Зеленограда за 2020-2022 годы

Вещество	NO	NO 2	SO 2	CH 4		O 3	CO
Количество измерений
2020	1030	1029	351	343			730
2021	2021	1023	351	717		361	1092
2022	978	978		313		335	1000
Средняя концентрация, мг/м3
2020	0,04	0,053	0,003	1,33		0,04	0,55
2021	0,04	0,053	0,0027	-		-	-
2022	0,0141	0,0182	-	-		-	-
		Максимальная концентрация,			мг/м3
2020	-	-	-	-		-	-
2021	-	-	-	-		-	-
2022	0,262	0,104	-	-		-	-
Количество измерений, когда зафисикровали превышение ПДК зв
2020	-	-	-	-		-	-
2021	-	-	-	-		-	-
2022	25	-	0	-		-	-

Результаты обследования передвижной экологической лабораторией ГПБУ «Мосэкомониторинг» подтвердили опреде- ленную правомерность заявлений граждан (рис. 2), что, вероятно, связано с неблагоприятными метеоусловиями.

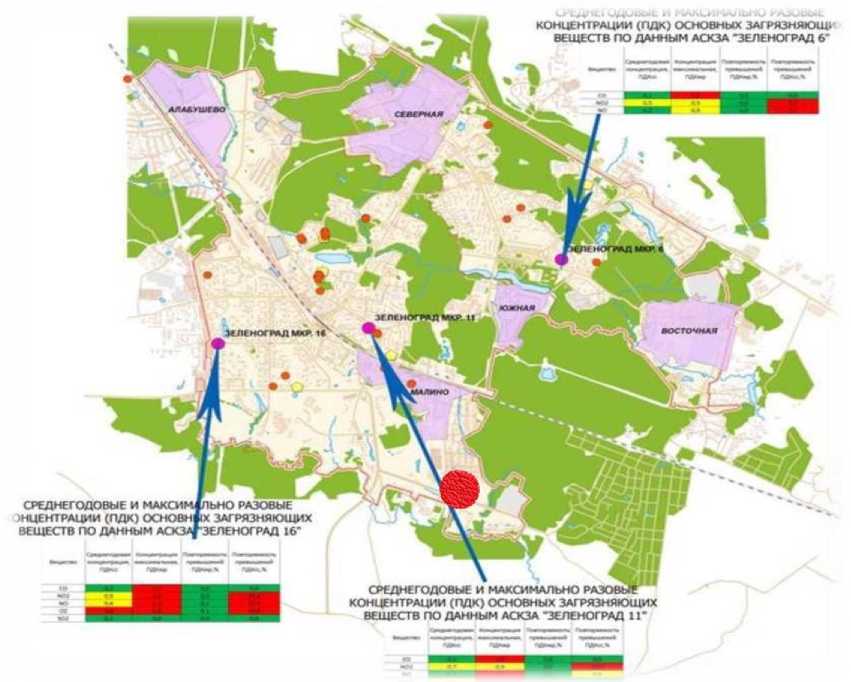
Рис. 1. Селитебные территории г. Зеленоград, обследованные передвижной экологической лабораторией ГБПУ «Мосэкомониторинг»

– место превышения ПДК загрязнителей

Последнее обстоятельство свидетельствует о необходимости математического и компьютерного описания рассеивания примесей и дальнейшей работы по повышению объективности и информативности системы экологического мониторинга.

Математическая модель распространения химических соединений в атмосфере основана на уравнении турбулентной диффузии [1, 2]:

8C(x,y,z,t) dt

+ div(f) + Л • С (х, у, z , t) = 0,

где C(x,y,z,t) - функция распространения концентрации загрязняющего вещества; ] -представляет собой сумму потоков диффузии: J=J1+J2 (молекулярной + турбулентной):

Л = С(х, у, z, t) • v(x, у, z), Л = -(К1 + К2) • grad(C(x,y,z, где XC(x,y,z,t) - описывает возникновение дополнительной концентрации примеси при воздействии на неё каких-либо погодных условий (осадки, туман и т.д.); -представляет собой поток молекулярной диффузии; - представляет собой поток турбулентной диффузии и имеет название закон Фика; Ki - коэффициент молекулярной диффузии, который отражает перенос вещества в нижний слой атмосферы; K2 – коэффициент турбулентной диффузии в случае анизотропной среды.

Далее уравнение (1) после математических преобразований принимает вид:

57 + ^«57 + МО 57 + ” z (t) 57 = 57^ + 57МО 57 ⁺ 57^ (0 g - ^x(t-)^c(^.  (2)

где t - время распространения примеси, с; (vx, vy, vz) - составляющие средней скорости перемещения вещества соответственно по направлению осей x, y, z , м/с; (kx, ky, kz) - горизонтальные и вертикальные составляющие компонента турбулентной диффузии (коэффициенты обмена), м2/с; К - коэффициент трансформации примеси по причине воздействия на неё атмосферных осадков (дождь, морось, туман), с-1; - первые частные производные по координатам, называемые градиентом концентрации, показывающие изменение скорости распространения концентрации

ЭС по направлению; ^- - первая частная производная концентрации по времени, которая определяет изменение скорости концентрации во времени.

Применяя различные допущения о реальных погодных условиях относительно уравнения (2), указав начальные и граничные условия и решив дифференциальное уравнение с частными производными второго порядка, получаем нестационарную функцию распространения химических веществ в атмосфере [1, 2]:

С(х, у, z, ))

М        ^(x-E x ^t)2

----------е 4kt 8(knt)³ / ²

2 (Z-H)² (Z+H)² ^е-ЧйКеЧк^ 4kt^v

где M - мощность непрерывного точечного источника (выбросы вещества в единицу времени), кг/с; t - время распространения вещества, с; k - коэффициент турбулентной диффузии, м²/с; v x - средняя скорость ветра в горизонтальном направлении, м/с; H - эффективная высота подъёма «факела», м.

Применение свёртки по времени к формуле (3) позволяет произвести расчёт концентрации газообразного вещества согласно модели Гаусса в любой расчётной точке независимо от времени при следующих условиях [1, 2]:

С (х, у, z)

М    ^Ех

=-- е 2k • ( 4itk         ^v

В функциональных зависимостях (3) и (4) определенные сложности может вызывать расчет коэффициента турбулентной диффузии в системе «воздух- загрязнитель», зависящего от метеоусловий (температуры воздуха, скорости ветра, наличия или отсутствия осадков). Он не является справочным и не может быть измерен.

• 1.    Источник функционирует практически непрерывно.

• 2.    Примесь однородна при отсутствии её потерь.

• 3.    Коэффициенты тензорной матрицы совпадают с главными осями системы координат.

• 4.    Концентрация примеси в выбросе падает по экспоненте.

• 5.    Имеется только турбулентная диффузия, а молекулярная пренебрежимо мала.

При этом стационарное решение уравнения в случае атмосферных осадков будет иметь вид [2]:

^x2+y2+(z-H)2

e -2k^(x2+y2+(z-H^2)‘(t,X+4k^)

+

1 e —k^(x2+y2+(z+H)2,(t’X+4'kA) A MA

^x2+y2+(z+H)2

Среди экспериментальных методов расчета данного коэффициента наиболее точным и охватывающим широкий спектр химических веществ является метод Бир-да-Гиршфельдера-Куртисса. Коэффициента турбулентной диффузии для двух неполярных газов здесь определяется из выражения [3]:

к =

0,002628

2 -П^(1,1) * ^{Р о}1,2 “ 1,2

I Т3(М1 + М2)

2М1М2  , где k – коэффициент диффузии, м2/с; p – давление, атм.; T – температура, K; M1, M2 – молекулярные массы газов 1 и 2; σ1,2 – постоянная сил, найденная по формуле Леннарда-Джонса, Å; – функция, значение которой берётся по справочной таблице; ε1,2 и σ1,2 – постоянные сил, Å, которая определяются по формулам Леннарда-Джонса:

_ 0-1+ 0-2 0 1,2 =   _?   ,

^ 1,2 = 7^ 1 • ^ 2 ,

где σ 1 , σ 2 , ε 1 , ε 2 – постоянные в уравнении Леннарда-Джонса.

Коэффициенты турбулентной диффузии для системы «воздух-загрязнитель» представлены в таблице 2.

Таблица 2. Коэффициенты турбулентной диффузии в системе «воздух- загрязнитель»

при различной температуре воздуха (метод Бирда-Гиршфельдера-Куртисса)

Загрязнитель	К 1 , 2 (T = 258 K), •IO 4, м2/с	К 1 , 2 (T = 273 K), •IO 4, м2/с	К 1 , 2 (T = 288 K), •IO4, м2/с
CO	0,158	0,174	0,192
CO2	0,116	0,128	0,142
NO	0,158	0,174	0,193
SO2	0,096	0,106	0,118
CH4	0,164	0,184	0,202

Используя показатели работы предприятия, розу ветров, информацию по концентрациям загрязнителей, построены поля рассеивания вредных примесей от промышленного предприятия ООО «Коронкер», расположенного на территории с наибольшим количеством заявлений граждан на загрязнение атмосферы. Унифицированная программа расчета за- грязнения атмосферы УПРЗА «ЭКОцентр – Стандарт» позволяет учитывать вышеперечисленные факторы влияния на рассеивание примесей [4].

Результаты расчетов распространения NO2 при неблагоприятных метеоусловиях с учетом фонового загрязнения представлены в виде полей рассеивания на рисунке 2.

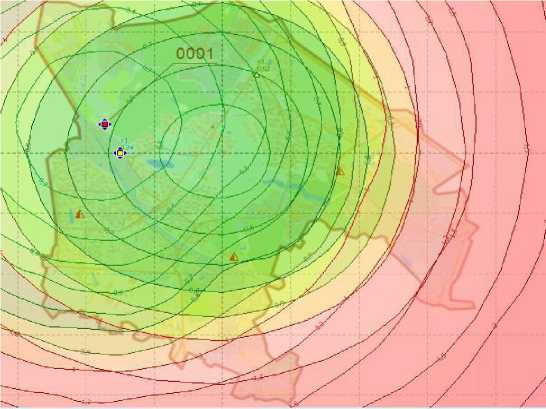
Рис. 2. Распространение NO 2 над территорией города при неблагоприятных погодных условиях (скорость ветра = 0,5 м/с, осадков – нет)

Рис. 3. Распространение HNO 3 над территорией города при неблагоприятных погодных условиях (скорость ветра = 0,5 м/с, осадков – нет)

Поля рассеивания концентрации загрязнителя учитывают характеристику предприятия: круглосуточный режим работы, количество труб (1 шт.), высоту трубы (H = 100 м), количество цехов (1 шт). Также программа позволяет учесть температуру выхода газоводущной смеси (Твых = 70 °С), внешнюю температуру окружающей среды (Tос = 70 °С), максимальную скорость ветра (v = 0,5 м/с), коэффициент, отвеча- ющий за рельеф местности (ȵ = 1), преобладающую розу ветров в городе и т.д.

Концентрация загрязнителя при отсутствии ветра и осадков, иными словами, при неблагоприятных условиях не превышает максимально разовые по нормативу (ПДК м.р. (NO 2 ) = 0,3 мг/м3).

Возможность химической реакции с образованием вторичного загрязнителя HNO 3 оценивается значением энергии Гиббса, определяемой из уравнения [5]:

AG = AH

-TAS,

где ΔH – энтальпия, кДж/моль;

ΔS – энтропия, Дж/(моль∙К);

T – абсолютная температура, К.

Зависимость (4) справедлива только для температуры воздуха 298 К.

AG_f = AH_r298 - T • AS_r ,298 - T(AaM 0 + AbM 1 + AcM 2 )

Члены уравнения Δa, Δb, Δc, M 0 , M 1 , M 2 при соответствующих температурах приводятся из справочных таблиц, которые не зависят о природы веществ, а зависят только от температуры.

Режим и основные параметры функционирования предприятия описаны к рис. 2. Расчет значения среднесуточной концентрации HNO3 находится из уравнения хи- мической реакции NO2 +H2O → HNO3 и принимается равной 2,472∙10-4.

Расчеты показывают, что превышение этого загрязнителя могут быть лишь незначительными, не выходя за границу предельно-допустимых. В то же время, эти расчеты наводят на мысль о том, что необходимо периодически строить поля рассе- ивания различных загрязнений и следить за их поведением в атмосфере [5].

Результаты расчетов свидетельствуют о незначительном загрязнении воздушного бассейна города, что соответствует общей статистике территориального органа Роспотребнадзора г. Зеленограде. Заявления граждан на определенный дискомфорт, вышениям ПДКзв., зафиксированным системой мониторинга и приведенным в таблице 1.

Взаимодействие химических соединений в реальности может повлечь появление и вторичного загрязнителя HNO 3 , но в условиях города, его концентрация будет незначительна.

следует, очевидно, отнести к редким пре-