Эконометрическое исследование влияния банковских кредитов на инвестиционную активность в России

Проводившиеся в 90-х годах прошлого столетия в России реформы были направлены на обеспечение финансовой стабилизации экономики, создание благоприятного инвестиционного климата и привлечение инвестиций как основы экономического роста, структурной перестройки и повышения благосостояния населения. Однако в настоящее время, несмотря на некоторое улучшение макроэкономических показателей, инвестиционные проблемы российской экономики продолжают стоять так же остро, как и несколько лет назад.

Актуальность проблемы финансово-кредитного обеспечения инвестиционного процесса обусловлена тем, что это один из фундаментальных факторов расширенного воспроизводства, роста источников инвестиций в экономику, устойчивого и безопасного развития России1. В то же время состояние инвестиционной сферы определяется множеством макроэкономических показателей (внутренний валовой продукт (ВВП), реальная ставка процента, объемы банковского кредитования экономики, уровень основного капитал и т. п.).

Цель настоящей статьи – исследовать, опираясь на эконометрический инструментарий, насколько существенно влияние основных макроэкономических показателей (ВВП, реальная ставка процента, кредит, основной капитал)2 на инвестиционную активность в России. Особый интерес вызывает определение влияния банковского кредита на стимулирование инвестиций в экономику страны, поскольку банковская система является одним из самых «естественных» инвесторов, главная из ее функций – перераспределение свободного капитала между участниками рыночных отношений.

Для достижения поставленной цели построим кредитно-инвестиционную модель и по результатам проведения статистических наблюдений определим количественное влияние ВВП, реальной ставки процента, банковского кредита, уровня основного капитала на инвестиционную активность в России.

Объектом эконометрического исследования выступают инвестиции в основной капитал, предметом – математический аппарат моделирования финансово-экономических факторов, влияющих на инвестиционную активность в России.

Для спецификации кредитно-инвестиционной модели воспользуемся следующими экономическими утверждениями:

• •    уровень инвестиций объясняется объемом выданных банковских кредитов³, величиной основного капитала, реальной ставкой процента и величиной изменения ВВП;

• •    с ростом объема выданных банками кредитов, уровня основного капитала, ВВП возрастает объем инвестиций в основной капитал;

• •    объем инвестиций в основной капитал возрастает при снижении реальной ставки процента.

Переведя перечисленные утверждения на «математический язык», получим следующий вид линейной модели множественной регрессии:

I t = а о + aC + a ₂ к , + a 3 R t + a 4 A Y + u,

E ( u , ) - 0                                                                         (1)

.E (ut И где It – инвестиции в основной капитал (млрд р.) на определенную дату;

Cr_t – объем предоставленных банками кредитов (млрд р.) на дату;

K_t – основной капитал (млрд р.) на дату;

R_t – реальная ставка процента (%) на дату – официальная ставка кредитования коммерческих банков со стороны Центрального банка Российской Федерации, скорректированная на уровень инфляции⁴;

A Y - изменение ВВП (млрд р.) на дату;

а ₁, a ₂, a ₃, a ₄ – коэффициенты , которые численно равны ожидаемому изменению объема инвестиций в основной капитал ( I_t ) в ответ на единичное изменение объема предоставленных банками кредитов ( Cr_t ), основного капитала ( K_t ), реальной ставки процента ( R_t ), ВВП ( A Y ). Соответственно, при этом a ₁ > 0, a 2 > 0, a ₃< 0, a ₄ > 0;

u_t – случайное возмущение (остаток) , отражающее влияние на искомую переменную I_t (инвестиции в основной капитал) неучтенных в модели факторов, которые зависят от социально-экономической ситуации в стране. Поскольку данная эконометрическая модель предполагает, что в среднем влияние неучтенных факторов на инвестиционную активность невелико, то ожидаемое среднее значение переменной u_t равно нулю E ( u_t ) = 0, а ожидаемое среднее значение квадрата переменной u_t равно неотрицательной константе ^ L (дисперсия случайной переменной u_t )⁵ E ( u_t ²) = ^ L . Иначе говоря, случайное возмущение предположительно гомоскедастично, и автокорреляция отсутствует;

о и - мера влияния на искомую неизвестную неучтенных факторов.

В представленной модели текущими значениями эндогенных переменных служат инвестиции в основной капитал (искомые неизвестные) I_t , предопределенными переменными (экзогенными) являются предоставленные банками кредиты Cr_t , основной капитал K_t , реальная ставка процента R_t , изменение объема ВВП A Y ( регрессоры ).

Кредитно-инвестиционная модель (1) является динамической и предназначена для прогноза значений текущей эндогенной переменной I_t по известным в периоде t значениям экзогенных переменных Cr_t , K_t , R_t , A Y . Спецификация экономической модели (1) имеет приведенный вид, так как в этой спецификации текущие эндогенные переменные являются явными функциями предопределенных переменных.

Статистическая информация, необходимая для исследования, представлена в таблице 1.

Таблица 1

Исходные данные ⁶

i §	2 го	>S О . I ci tn о 3 и t о § tn -r it 1	X £ Ц Ct	lit t s t ° e s os sc	< O's tn ► tn S' О ^~ CR S s &	Реальный объем произведенного ВВП в среднегодовых ценах 2000 года (Y), млрд р.	Изменение реального объема произведенного ВВП ( Δ Y), млрд р.
1	I квартал 2000 года	166	909	3 725	38	1 651	55
2	II квартал 2000 года	236	1 039	4 151	27	1 732	81
3	III квартал 2000 года	330	1 195	4 225	23	2 020	288
4	IV квартал 2000 года	433	1 492	4 504	21	1 902	-118
5	I квартал 2001 года	230	1 812	4 621	20	1 728	-174
6	II квартал 2001 года	319	2 077	4 893	20	1 820	91
7	III квартал 2001 года	421	2 375	5 602	20	2 142	322
8	IV квартал 2001 года	534	2 730	5 125	21	1 988	-154
9	I квартал 2002 года	270	2 899	5 998	21	1 794	-194
10	II квартал 2002 года	376	3 077	6 130	19	1 900	106
11	III квартал 2002 года	495	3 376	6 150	18	2 237	337
12	IV квартал 2002 года	621	3 680	6 241	16	2 111	-126
13	I квартал 2003 года	330	3 919	6 342	13	1 931	-180
14	II квартал 2003 года	471	4 281	6 425	15	2 052	121
15	III квартал 2003 года	609	4 877	6 594	15	2 376	325
16	IV квартал 2003 года	777	5 503	7 014	13	2 274	-102
17	I квартал 2004 года	373	5 889	7 498	10	2 072	-203
18	II квартал 2004 года	528	6 634	7 520	11	2 206	134
19	III квартал 2004 года	670	7 354	7 531	11	2 545	339
20	IV квартал 2004 года	852	8 143	7 576	9	2 427	-118
21	I квартал 2005 года	408	9 119	7 695	8	2 168	-259
22	II квартал 2005 года	578	9 754	7 812	10	2 342	174
23	III квартал 2005 года	753	10 748	7 750	12	2 510	168

Наличие взаимосвязи между исследуемыми переменными и ее качество представлены на рисунках: влияние банковских кредитов на инвестиционную активность в России – на рисунке 1, влияние реальной ставки процента на инвестиционную активность в России – на рисунке 2, влияние уровня основного капитала и реального объема произведенного ВВП на инвестиционную активность в России – на рисунке 3.

• ⁶ Расчеты произведены по данным Центрального банка Российской Федерации и Федеральной службы государственной статистики.

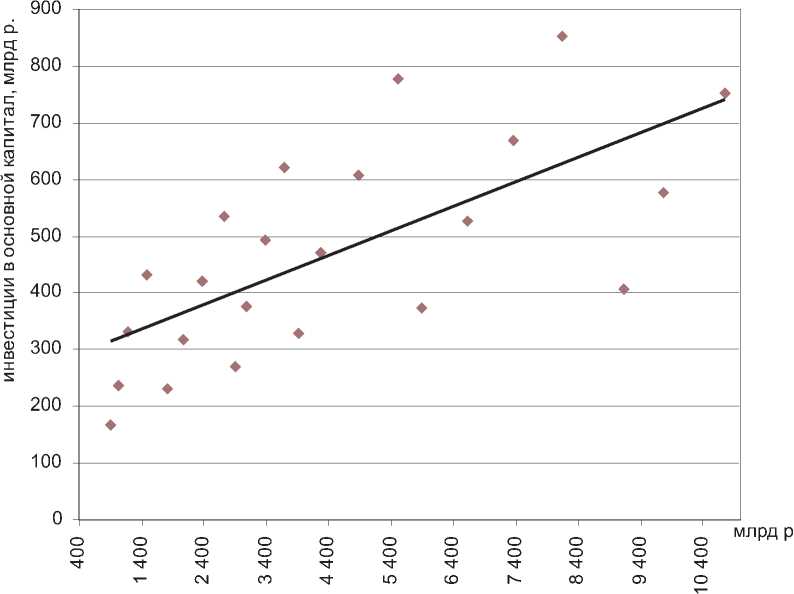
Рис. 1. Влияние банковских кредитов на инвестиционную активность в России

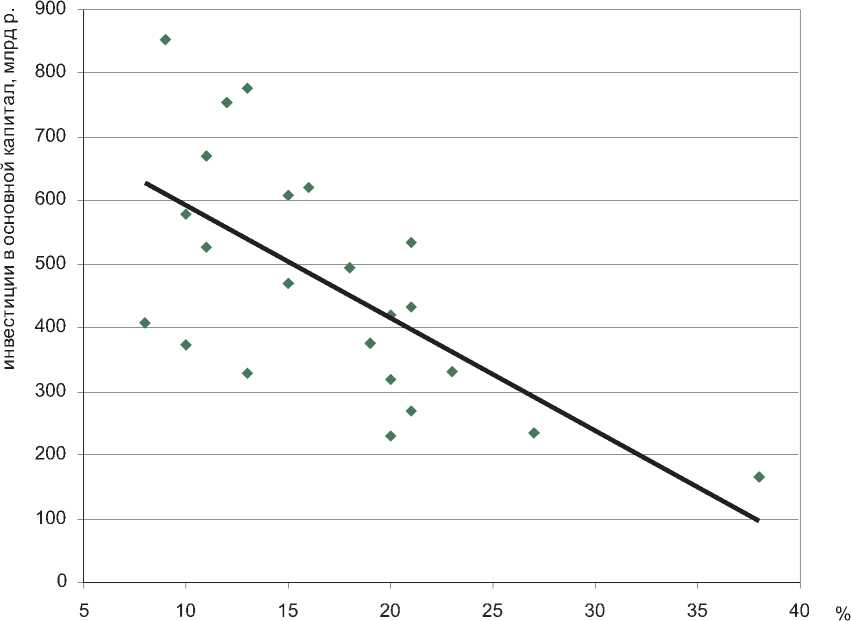
Рис. 2. Влияние реальной ставки процента на инвестиционную активность

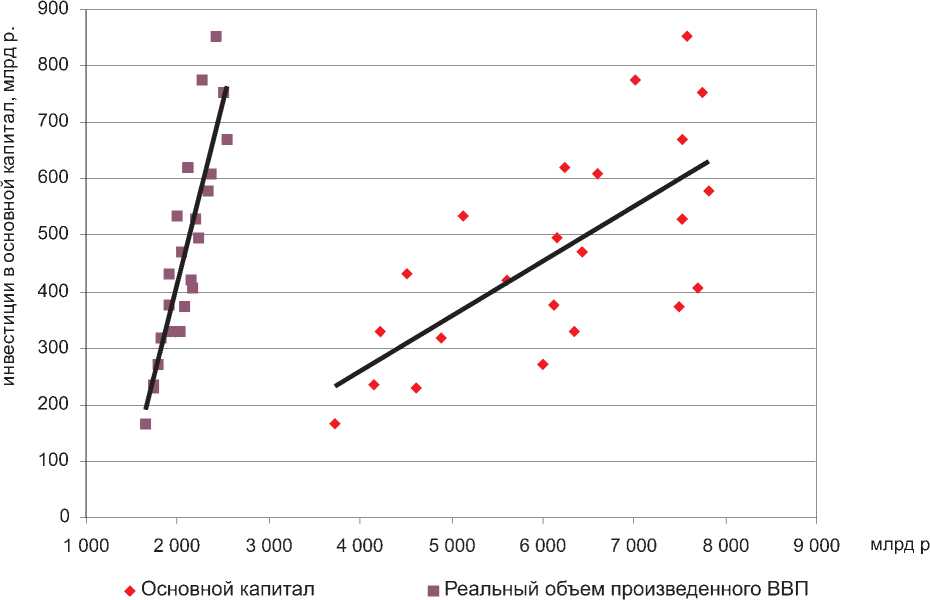
Рис. 3. Влияние уровня основного капитала и реального объема произведенного ВВП на инвестиционную активность России

На рисунках точки, составляющие графики, не располагаются на прямой, а это значит, что между переменными Cr t , K t , R t , A Y и I t отсутствует функциональная зависимость. Облако точек вытянуто (хаотично рассеяно) вдоль прямой. Примем их как законы, по которым меняется I t в ответ на изменение Cr t , K t , R t , A Y .

Существует некоторая выборка значений переменных модели (1):

( Cr i , K i , R i , A Y i , 1 1 ), ( Cr 2 , K 2 , R ₂, A Y 2 , 1 ₂), .... ( Cr_n , K n , R n , A Y n , I n ).

Эта выборка получена на этапе наблюдения объекта оригинала и предназначена для оценки следующих параметров: a 0 , a 1 , a ₂, a 3 , a 4 , ^ u .

В рамках модели (1) величины, составляющие выборку (2), связаны следующей системой линейных алгебраических уравнений (системой уравнений наблюдения объекта) или схемой Гаусса-Маркова:

1 1 = a ₀ + a ₁ Cr ₁ + a ₂ K 1 + a ₃ R 1 + a 4 A Y + u 1

166 = a ₀ + a 1 909 + a ₂ 3725 + a 3 38 + a ₄ 55 + u 1 ,

236 = a ₀ + a 1 1039 + a 2 4151 + a ₃27 + a 4 81 + u 2 ,

753 = a _n + a 10748 + a₉ 7750 + a, 12 + a ₄168 + u_n 01       2      3    4      n

1 ₂ = a ₀ + a 1 Cr₂ + a ₂ K ₂ + a ₃ R ₂ + a ₄ A Y 2 + u ₂

I n = a 0 ⁺ a 1^Crn ⁺ a 2 K n ⁺ a 3 R n ⁺ a 4 ^A Y n ^{+ u}n

Компактная запись этой схемы может быть представлена следующим образом:

/ = Xzi + й , где I = (I1, I2, …, In)T – вектор известных значений эндогенной переменной It модели: T = (166, 236, _, 753)T;

й = ( u 1 , u ₂, ^ u_n ) T - вектор неизвестных значений случайных возмущений u t ;

⎡1 909 3725 38 55 ⎤ ⎡1 Cr1 K1 R1 ΔY1⎤ ⎢⎢1 1039 4151 27 81 ⎢⎢1 Cr2 K2 R2 ΔY2 ⎥⎥ Х= ... ⎢⎢1 .... 9754 .... 7812 ... 12 ... 174 ⎥или ⎢ ... ⎢1 .... Crn-1 .... Kn-1 ... Rn-1 ... ΔYn-1⎥ – матрица известных ⎢⎣1 10748 7750 12 168⎦ ⎢⎣1 Crn Kn Rn ΔYn ⎥⎦ значений предопределенных переменных, расширенная столбцом единиц;

a = ( a 0 , a 1 , а 2 , а 3 , а 4 ) T - вектор неизвестных коэффициентов уравнения модели, подлежащий оцениванию по выборке (2).

Оценку (приближенное значение) вектора а обозначим а = ( а 0 , 01 1 , а ₂, а ₃, а ₄ ) T , а символом бU - оценку дисперсии случайного остатка и модели (или меру влияния на объем инвестиций в основной капитал не учтенных в модели факторов).

Используя функцию «ЛИНЕЙН» электронных таблиц Excel, вычислим эти искомые оценки (табл. 2).

Таблица 2

	а 4	а 3	а 2	а 1	а 0
	0,16	-7,81	0,02	0,02	401,12
S ai , I = 0,…4	0,15	10,81	0,08	0,03	579,81
R 2	0,53	140,03				r-v σ u
F	5,12	18,00				σ u
	401425,79	352942,78
	RSS	ESS
F крит =	2,93			K = 4	n = 23
DW	1,14			d L	d u
TSS = RSS + ESS	754368,57			0,99	1,79
R2 = RSS/TSS	0,53

Примечание: В таблице используются символы, имеющие следующие значения:

S_ai – средние квадратические ошибки оценок коэффициентов a ₀, a ₁, a ₂, a ₃, a ₄;

F – случайная переменная, используемая для проверки модели на адекватность при выполнении F -теста;

RSS – объясненная регрессией сумма квадратов отклонений;

ESS – необъясненная регрессией сумма квадратов отклонений;

TSS – общая сумма квадратов отклонений зависимой переменной от ее выборочного значения;

DW – случайная величина, используемая для проверки модели на адекватность в тесте Дарбина-Уотсона;

d_L , d_u – пара констант, необходимая для выполнения теста Дарбина-Уотсона;

R ² – коэффициент детерминации;

а₀ = 401; а 1 = 0,02; а ₂ = 0,02; а₃ = -7,81; а₄ = 0,16; б u = 140,03; б u = 18.

С помощью функции «ЛИНЕЙН» вычислим средние квадратические ошибки оценок коэффициентов:

Sa ₀ = 579,81; Sa ₁ = 0,03; Sa ₂ = 0,08; Sa ₃ = 10,81; Sa ₄ = 0,16.

Финансово-экономические модели признаются адекватными (пригодными для работы), если вычисляемые по моделям значения эндогенных переменных отличаются от их реальных значений на допустимые величины, то есть применительно к модели (1) окажется справедливым неравенство:

I It - It | — eкрит (It )’ где eкрит (It) - критическая ошибка прогноза.

Произведем тестирование адекватности предпосылок теоремы Гаусса-Маркова о го-москедастичности и некоррелированности случайных возмущений в уравнениях наблюдений объекта.

Тест Голдфелда-Квандта

Этот тест предназначен для проверки предпосылки теоремы Гаусса-Маркова о гомос-кедастичности случайных возмущений в уравнениях наблюдений объекта, то есть для проверки того, что:

o ²( u 1 ) = o ²( u 2 ) = _ = o ²( u 23 ) = o ².                                                                    (3)

Выполним тест Голдфелда-Квандта по следующим этапам:

• 1)    упорядочим таблицу исходных данных (табл. 1) по возрастанию модуля значений предопределенных переменных модели (1) и разобьем ее на 2 части. При этом в первую часть должно быть включено не более n /2 значений выборки ( n ’⁷ = 23/2 = 11,5) а во вторую – оставшиеся значения (с 12 по 23);

• 2)    по первым n ’ упорядоченным уравнениям наблюдений объекта, где k <  n ’ < = n /2, k = 4 – количество оцениваемых коэффициентов (2), вычислим методом наименьших квадратов оценки параметров модели величину ESS 1 = X U 2 , где u_t = I t -1 .

Применим функцию «ЛИНЕЙН» для каждой части таблицы 18. Исходные данные и полученные значения представлены в таблицах 3 и 4;

Таблица 3

	а 4	а 3	а 2	а 1	а 0
	0,168813785	-10,7372	-0,19858	0,221773	1110,505
S ai , i = 0,…4	0,155842767	7,435107	0,139294	0,133996	526,3116
R 2	0,625198885	92,30101				<-v 0 u
F	2,502122564	6				0 u
	85267,10084	51116,86
	RSS 1	ESS 1

Таблица 4
	а 4	а 3	а 2	а 1	а 0
	-0,111860217	69,23423	0,263007	0,018244	-2252,84
S ai , i = 0,…4	0,368106765	59,23346	0,344755	0,053381	2854,679
R 2	0,324217716	170,987				σ u
F	0,839591412	7				σ u
	98187,04919	204655,9
	RSS 2	ESS 2

• 3)    вычислим значения следующих показателей:

GQ = ESS ₁/ ESS ₂ = 0,25;

1/ GQ = ESS 2 / ESS 1 = 4,0.

Используя функцию «FРАСПОБР», определим величину F _крит = 7,19;

• 4)    предпосылку теоремы Гаусса-Маркова (3) можно считать адекватной, если:

GQ < = F крит ;

• 1    / GQ < = F крит .

В нашем случае GQ <  F _крит; 1 / GQ <  F _крит.

Таким образом, можно сделать вывод о гомоскедастичности случайных возмущений в уравнениях наблюдений с вероятностью в 99 процентов.

Тест Дарбина-Уотсона ( DW )

Этот тест предназначен для проверки третьей предпосылки теоремы Гаусса-Маркова, точнее, частного случая этой предпосылки:

Cov ( u_i , u_j ) = 0 при j = i – 1.                                                                       (4)

Невыполнение этого условия вызывает негативные последствия для оценок параметров модели последствия. Тест выполняется следующим образом:

• 1)    вычисляется значение случайной величины DW (см таблицу 2): n

Z ( Ut - u t -1 ) 2

DW = ^{t = 2}            = 1,14.

_n        ,.

∑ u t ² t =1

Из таблицы, составленной Дарбиным и Уотсоном⁹, выбирается по значению n = 23 и количеству k = 4 объясняющих переменных пара констант – d_L , d_u . В нашем случае d_L = 0,99, d u = 1,79;

• 2)    проверяется, в какой из пяти интервалов отрезка от 0 до 4 попала величина DW :

M] М2       М3       M4 M5

r<--------->T<--------->T<---------- 1---------- >T<----------->T<-----------

0 dt d_u 2     4- d_u 4-dt 4

Если значение показателя DW попадает в подмножество М ₁, то корреляция остатков положительна, если в подмножество М ₂ или М ₄, то принять решения об адекватности или неадекватности предпосылки (4) нельзя. Если DW окажется в M ₅, то корреляция остатков отрицательна, маловероятна.

Предпосылка о некоррелированности случайных возмущений считается подтвержденной, адекватной, если величина DW попадает в интервал M ₃.

В нашем случае DW = 1,14 попадает в интервал M ₂. Следовательно, определить, выполняется ли предпосылка теоремы Гаусса-Маркова о некоррелированности случайных возмущений в уравнениях наблюдений объекта, невозможно, что объясняется наличием проблемы систематического несоответствия экономико-статистических данных, публикуемых в отечественной литературе.

Исследование качества спецификации линейной эконометрической модели: коэффициент детерминации и F -тест

Для исследования способности экзогенных переменных объяснять в рамках модели значения эндогенных переменных предназначен коэффициент детерминации R ² – это объясненная регрессором доля эндогенной переменной I_t . R ² зависит от выборки и, следовательно, является случайной переменной, что снижает уровень объективности заключения о качестве спецификации модели. F -тест придает суждению о качестве спецификации модели объективный характер.

Как уже определено в таблице 2, коэффициент детерминации R2 = RSS/TSS, где TSS = RSS + ESS = £ (li - 7 )2 ;

i =1

94          _              94          _    94

RSS = ^ ( I t - T )=, ESS = ^ ( 1, - I t ) = £ u? . t =1                                     t =1                       t =1

Из смысла величины R ₂ вытекает неравенство 0 <  R ₂ <  1.

Если R ² = 1, то выбранные исходные данные (экзогенные переменные) полностью объясняют в рамках рассматриваемой модели величину I_t . Если R ² = 0, это значит, что выбранные экзогенные переменные модели не способны объяснить искомую переменную I_t .

Используя функцию «ЛИНЕЙН», мы вычислили коэффициент детерминации: R ² = 0,5321 (табл. 2). Следовательно, экзогенные переменные способны объяснять эндогенную переменную I_t на 53,21 процента.

Пусть R ² = 0. Это значит, что существует гипотеза H ₀ : a ₁ = a ₀ =…= a_k = 0.

В нашем случае все предпосылки теорем Гаусса-Маркова справедливы для модели (1), а случайные остатки в уравнения наблюдений распределены по нормальному закону.

R ² / k

(1 - R 2 )/ [ n - ( к + 1)

Тогда, если гипотеза H0 справедлива, то случайная переменная F = обладает законом распределения Фишера с числом степеней свободы у1 = к, у2 = n - (к +1), где n = 23, k = 4.

Используя функцию «ЛИНЕЙН», мы получили, что F = 5,12 (табл. 2). При этом у 1 = 4, Y 2 = 18. Значит, F к _рит = 2,93 (таблица «95-процентные квантили распределения Фишера, ^ к _рит¹⁰.»¹¹.

Таким образом, F = 5,12 >  F _крит = 2,93, следовательно, в рамках оцененной модели регрессоры обладают способностью объяснить значения ее эндогенной переменной.

Как уже отмечалось, модель именуется адекватной, если прогнозы значений эндогенной переменной согласуются с ее наблюденными значениями. Проведем процедуру интервального прогнозирования значений эндогенной переменной. Результаты наблюдений (выборку) разделим на два класса. В первый класс, именуемый обучающей выборкой, включим основной объем результатов наблюдений оригинала (95%) выборки. Оставшиеся результаты наблюдений, например Cr , K , R , A Y , I за III квартал 2005 года, составят контролирующую выборку. По обучающей выборке оценим модель.

Зададимся доверительной вероятностью:

Р = 0,95; y 2 = n - ( к + 1 ) = 18; t _кр ит = 2,1.

Определим доверительный интервал для прогноза:

Qp tkpum Sp ’ Ip + tkpum Sp ) , где tкрит – коэффициент Стьюдента (или двухсторонний квантиль распределения Стьюдента);

S_p – среднеквадратическое (стандартное) отклонение прогноза, вычисляемое по формуле:

Sp = SE^q0, где q0 = XT (xtx )-1 X0, тогда: ^^.                                          ^^.

I p - t kpum S p < I < I p + t kpum S p или 303,66 < 753 < 1 082,12.

Значение эндогенной переменной 753 попадает в доверительный интервал (303,66; 1 082,12), поэтому оцененная модель адекватна, может быть использована для изучения объекта-оригиала: прогноза инвестиций в основной капитал по величине выданных банками кредитов, величины инвестиций в основной капитал, реальной ставки процента и изменения объема ВВП.

Поскольку средняя квадратическая ошибка оценки коэффициента а ₀ ( S_{a 0} = 579,81) значительно превышает величину оценки а ₀ (г а ₀ = 401), и в экономике любой страны уровень основного капитала, объем ВВП, реальная ставка процента не могут принимать нулевые значения, целесообразно исключить коэффициент а ₀ из кредитно-инвестиционной модели.

Исключив коэффициент а ₀ из кредитно-инвестиционной модели, вычислим с помощью функции «ЛИНЕЙН» оценки а₀ , И 1 , И 2 , И₃ , И ₄ (табл. 5).

Таблица 5

	а 4	а 3	а 2	а 1
	0,145636047	-1,082743993	0,068283825	0,013717376
S ai , i = 1,…4	0,148048908	4,653649553	0,027844506	0,02260187
R 2	0,937602116	138,0936095			° и
F	71,37437626	19			^ и
	5444393,165	362327,0548
	RSS	ESS

Таким образом, средние квадратические ошибки исследуемых в модели переменных ( S_ai ) более адекватно отражают изменение уровня банковского кредита, основного капитала, реальной ставки процента, объема ВВП.

Увеличение объема выданных банками кредитов на 1 миллиард рублей в среднем привело к росту инвестиций в основной капитал на 14 миллионов рублей. Снижение реальной ставки процента за рассматриваемый период с 38 до 12 процентов увеличило объем инвестиций в основной капитал на 1,08 миллиарда рублей, рост уровня основного капитала – 7 миллионов рублей, увеличение объема ВВП вызвало рост инвестиций всего лишь на 146 тысяч рублей.

Так, изменение основных макроэкономических параметров с 2000 по 2006 год привело в совокупности к росту объема инвестиций в основной капитал всего лишь на 1,1 миллиарда рублей, а это является недостаточным, учитывая, что изношенность основных фондов в ряде отраслей экономики составляет более 80 процентов.

Вместе с тем на величину инвестиций в основной капитал, помимо исследуемых в кредитно-инвестиционной модели переменных, оказывают влияние и другие неучтенные факторы, их действие в стоимостном выражении составляет 140 миллиардов рублей, что в 120 раз превышает факторы, которые в инвестиционном процессе в условиях рыночной экономики должны играть более существенную роль (ВВП, реальная ставка процента, кредит, основной капитал).

В экономике сохраняются негативные тенденции, сдерживающие эффективное развитие инвестиционной сферы. Несмотря на существующую неравномерность инвестиционной активности в отраслях экономики, пока не создан отлаженный механизм перелива капитала; инвестиции развиваются преимущественно благодаря капитальным затратам крупных экспортеров, в результате инвестиционная сфера остается зависимой от внешнеэкономической конъюнктуры.

Преодоление этих проблем возможно лишь при формировании механизмов, способствующих высвобождению имеющихся средств и расширению возможностей их использования. Таким образом, привлечение банковских инвестиций в реальный сектор экономики является одной из ключевых проблем современного этапа развития России. В связи с этим возникает необходимость более широкого использования банковского кредита как инвестиционного ресурса.

Несмотря на то, что по прошествии 5–8 лет после дефолта российские банки показывают высокие темпы роста, которые опережают темпы роста ВВП в 4–5 раз, масштабы банковской системы и объем выдаваемых кредитов неадекватны потребностям производства, а количественные и качественные показатели российских банков неадекватны требованиям реального сектора экономики и населения. В нашей стране отношение кредитов нефинансовым предприятиям к ВВП составляет 20 процентов, тогда как в развитых странах этот показатель превышает 50 процентов.

Очевидно, необходимо преодолеть отставание в банковской сфере, создать экономическую среду, стимулирующую ее развитие, следовательно, стимулирующую и развитие в инвестиционной сфере, обеспечивающую достижение высоких и устойчивых темпов экономического роста.

Для переориентации финансовых потоков в направлении реального сектора экономики через российский банковский сектор требуются инструменты, снижающие риски инвестирования. Одними из таких инструментов должны быть разработка долгосрочной промышленной и структурной политики, а также кредитно-финансовая, налоговая поддержка со стороны банков и прочих финансовых институтов, а также государства участников инвестиционных проектов в приоритетных отраслях экономики. Существенную помощь в развитии кредитования может оказать совершенствование банковского законодательства, нормативного и методического обеспечения.

«Исторический опыт свидетельствует о том, что кредит приносит пользу в тех случаях, когда в обществе созданы необходимые предпосылки, в частности, есть хорошая (строгая и ясная) законодательная база, возможность быстро добиться судебного решения, создающего основы для общественного доверия. Слабоэффективным, чаще всего беспо- лезным, может оказаться применение кредита там, где народ не умеет пользоваться плодами своих земель, в обществе нет должной соревновательности, конкуренции и, напротив, властвует бюрократия, сложилась несправедливая налоговая система, плохая инфраструктура производства (неразвитые коммуникации, плохие дороги, слабая железнодорожная сеть и т. п.), где, наконец, деньги не прибывают, а уходят или, как говорят, наблюдается отрицательный денежный поток, приводящий к уменьшению богатства регионов, провинций и стран»12.

Если в этих условиях не предпринимать радикальных шагов по восстановлению значимости кредита и придерживаться созерцательной, пассивной политики, то мы и дальше не сможем использовать созидательный ресурс, свойственный кредиту, неизбежно потеряем возможность существенно ускорить развитие национальной экономики.

Некоммерческое партнерство «МЕЖДУНАРОДНЫЙ ЦЕНТР ОБРАЗОВАНИЯ И ТУРИЗМА»

Приглашает принять участие в семинаре 2-6 апреля 2007 года, город Москва

ПРАКТИЧЕСКИЕ ВОПРОСЫ И РЕКОМЕНДАЦИИ В СФЕРЕ ОБОРОТА И ИСПОЛЬЗОВАНИЯ ЗЕМЕЛЬНЫХ УЧАСТКОВ, ЗАНЯТЫХ ОБЪЕКТАМИ НЕДВИЖИМОСТИ.

НОВОЕ В ЗАКОНОДАТЕЛЬСТВЕ

• •    правовое регулирование оборота и использования земельных участков, занятых объектами недвижимости

• •    правовой режим земель, виды прав на земельные участки и обременения в использовании земель

• •    виды сделок с земельными участками и объектами недвижимости, порядок их совершения, состав и требования к документам

• •    особенности государственной регистрации прав на земельные участки и объекты недвижимости компаний энергетического и нефтегазового комплекса

• •    порядок формирования земельного участка, изготовление и утверждение проектов границ земельного участка, межевание земельного участка

• •    подготовка описания земельного участка для целей государственного кадастрового учета земель

• •    порядок оформления и переоформления прав на земельные участки и объекты недвижимости, расположенные на них

• •    предоставление земельных участков для строительства линейных объектов

• •    порядок перевода земель или земельных участков из одной категории в другую

• •    постановка земельного участка на государственный кадастровый учет, состав и требования к документам

• •    формирование объекта недвижимости как объекта государственного технического учета

• •    рыночная оценка земельных участков и объектов недвижимости. Государственная кадастровая оценка земель разных категорий для целей налогообложения

• •    судебно-арбитражная практика разрешения споров в сфере оборота и использования земельных участков, занятых объектами недвижимости

ЗАЯВКИ НА УЧАСТИЕ И ПОДРОБНАЯ ИНФОРМАЦИЯ:

125445 Россия, г. Москва, ул. Смольная, д. 24 А, офис 1415

тел. (495) 980-0897,136-6455

e-mail: , сайт: