Эконометрическое моделирование жизненного цикла нефтяного месторождения

В настоящее время при математическом моделировании процессов разработки нефтяных месторождений превалирует дедуктивный подход, заключающийся в расчете фильтрационных течений в реальном пласте на основе численного решения общих уравнений движения жидкостей и газов в пористой среде [1].

Опыт моделирования сложных природных объектов, накопленный в различных областях науки, показывает, что такой подход, несмотря на свою привлекательность, может иметь только ограниченное применение. Основной трудностью детерминированных моделей являются отсутствие достоверной информации о детальном геологическом строении пласта и большие погрешности в промысловых данных. Кроме того, такие модели не описывают особенности эксплуатации месторождений, определяемых его владельцами с учетом его финансовых возможностей и потребностей рынка в нефти, а также не могут спрогнозировать динамику аварий, влияние сезонных ограничений и человеческого фактора [1].

Для моделирования добычи нефти с месторождений можно использовать и феноменологический подход, в соответствии с которым детально не анализируются внутренние процессы моделируемого явления. «Феноменологическим» подход называют, когда получаемое описание явления не претендует на установление причинно-следственной связи. Феноменологические модели оказываются весьма плодотворными, когда детальная картина явления слишком сложна. При использовании феноменологических моделей история нефтяного месторождения рассматривается как история всего месторождения в целом, а не делится на истории отельных скважин, пластов и объектов разработки. Накопленная статистика по добыче на разных нефтяных месторождениях позволяет применить феноменологический подход для построения математической модели «жизненного цикла месторождения» в параметрическом виде – как модели динамики добычи нефти, где объем добычи является функцией только одного параметра – времени.

Цель настоящей статьи – разработка феноменологических параметрических моделей, которые могут быть использованы для повышения эффективности прогнозирования показателей добычи и реализации нефти с обособленных месторождений. Такие модели должны обеспечить прогнозирование объемов добычи нефти на отдельном месторождении или на нефтеносном районе на основе предыдущей статистики добычи, в том числе и в случае, ко- гда геологическая информация об объекте отсутствует или обладает низкой точностью, или геологическая модель сложна в связи с масштабом моделируемого объекта.

Для достижения поставленной цели необходимо решить следующие задачи:

• -    предложить ассортимент феноменологических моделей, пригодных для описания показателей добычи нефти;

• -    разработать алгоритм идентификации параметров предложенных моделей на основе известных статистических данных динамики добычи;

• -    реализовать алгоритм моделирования и прогнозирования показателей добычи нефти

в виде компьютерных программ.

Одной из наиболее известных моделей описания истории добычи нефти является модель Хабберта [2], которую с учетом аддитивного вхождения стохастической компоненты в модель можно записать в виде [3]:

Y (t ) =

у„ ■ 2

____ max ____

1 + ch ( ° ( t — t Q ) )

+ 5 ⁽ t ) .

Модель Хабберта широко используется для прогнозирования пика добычи нефти и яв ляется признанной эмпирической моделью описания динамики добычи нефти [4].

Вероятно, второй моделью, которую можно применить для описания добычи нефти с месторождения, является модель С.П. Капицы [5]:

Y ( t ) =

Y max "  °

( t ^— t Q ) ^{2 +} ° ²

⁺ ^ ⁽ t ) .

В [5] показано, что модель (2) хорошо описывает динамику численности народонаселения Земли, а в [1] показано, что ее можно использовать на ранних стадиях разработки крупных месторождений для обоснованного прогноза добычи нефти.

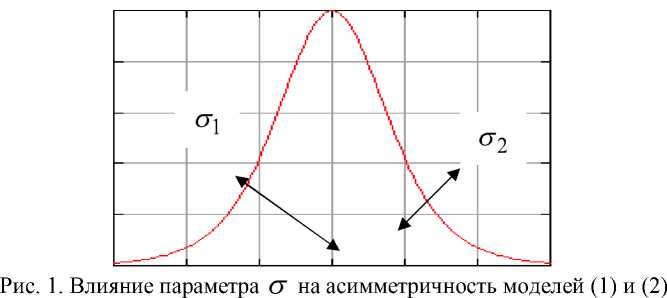
Модели (1) и (2) имеют колоколообразный вид, параметры tQ и Ymax определяют со- ответственно абсциссу и ординату вершины, а параметр ° регулирует наклон участков кривой роста и падения.

В 2QQ7 г. Брандт [6] использовал модель Гаусса с изменяемым во времени по закону Верхулста наклоном °(t). Брандт исследовал 67 месторождений добычи нефти, пик кото рых уже наступил, и установил, что уровень добычи нефти несимметричен относительно своего пика - средняя величина падения уровня добычи (2,6%) была примерно на 5% ниже, чем средняя величина роста (7,8%) добычи до пика. Такая асимметрия может быть обусловлена экономическим желанием увеличения добычи нефти и сохранением максимально возможного уровня добычи и используемыми вследствие такого желания технологическими решениями.

Поэтому для описания добычи нефти модели (1) и (2) целесообразно дополнить законом изменения параметра °(t), в которых параметр °(t) во времени изменяется по логи стическому закону - от °1 на этапе роста до °2 на этапе падения. Причем скорость этого перехода может быть задана специальным параметром °т . Для описания изменения °(t) можно воспользоваться логистическими функциями, например Ричардса, Верхулста и Гом- перца.

Рассмотрим следующие законы изменения ° во времени:

1) неизменный (симметричный колоколообразный вид):

° ( t ) = ° 1 = ° 2 = const ^;

2) Ричардса:

° ⁽ t ) = ° 1 ⁺ ( ° 2

—

t — t.

— ° 1 ) 1 + e ° ^т

— 1/ ° т 1

• 3)    Верхулста: _р ( t ) = _р + ^р 2 - ^р 1 ;                                                     (5)

t - t о

1 + e ^P T

- 0,7exp( - t t ⁰ )

.

• 4)    Гомперца: р ( t ) = р 1 + ( р 2 - р 1 ) e           ° T

Модели (1) и (2) при неизменном (3) значении р симметричны и имеют 3 требующих определения параметра ( t о , T m ax , р ), а при изменении р ( t ) по законам Верхулста (5) и Гомперца (6) обладают уже 5 неизвестными (требующих определения) параметрами. При изменении р ( t ) по закону Ричардса (4) неизвестными будут уже 6 параметров из-за присутствия параметра р т 1 , описывающего уровень асимметрии логистической кривой. В итоге моделирование динамики добычи нефти с месторождения будем проводить с помощью 8 моделей, являющихся сочетаниями 2 моделей динамики добычи нефти с 4 вариантами их асимметрии.

Для поиска неизвестных параметров моделей используется генетический алгоритм – эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путем случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию [8, 9].

Генетический алгоритм состоит из основных 4 стадий:

• 1.    Случайным образом генерируется конечный набор пробных решений – первое поколение.

• 2.    Оценка приспособленности решений текущего поколения производится исходя из заданного критерия. В случае идентификации параметров функции может быть использован критерий минимума суммы квадратов отклонений модельной функции от исходного набора данных.

• 3.    Осуществляется выход из алгоритма, если удовлетворен критерий останова, иначе п.4.

• 4.    Генерация нового поколения происходит посредством операторов селекции, скрещивания и мутаций, после чего переход к п. 2.

В процессе селекции отбирают только несколько лучших пробных решений на основании заданного критерия, остальные решения не используются. Скрещивание за место пары решений создает другую пару, коэффициенты которой вычисляются на основании коэффициентов исходной пары с помощью какого-либо оператора, к примеру, путем нахождения среднего. В результате серии скрещиваний размер прореженной популяции увеличивается до исходного. Мутация случайным образом изменяет коэффициенты решений, выводя алгоритм из состояний определения локальных экстремумов.

Для идентификации параметров моделей (1) и (2) с изменением параметра р ( t ) по законам (3), (4), (5) и (6) была использована инструментальная реализация генетического алгоритма – функция gatool системы MATLAB.

Используя данные об объемах добычи нефти на 2 месторождениях ОАО «Роснефть» (С-ском, М-ском), получим параметрические модели добычи, оценим точность моделирования и прогнозирования кривых жизненного цикла добычи нефти этих месторождений ранее описанными моделями и выберем из них наилучшую.

Параметры полученных моделей С-ского и М-ского месторождений приведены в таблицах 1 и 2.

Первое сравнение рассмотренных моделей проведем путем сравнения значений коэффициентов детерминации R 2 как наиболее широко используемых в эконометрике [7].

Из таблиц 1 и 2 видно, что симметричные модели обладают более низким коэффициентом детерминации. Модели Хабберта и Капицы, обладающие асимметрией по законам Верхулста, Ричарда и Гомперца, показывают примерно одинаковые результаты точности аппроксимации (средний уровень R 2 = 0,97). Модели с асимметрией Ричардса являются более сложными, содержат большее число параметров и могут более гибко описывать динамику добычи нефти, что и проявляется в большем значении коэффициента R 2 .

Точность прогнозирования оценим с помощью второго коэффициента Тейла Т 2 , вычисляемого по формуле

l

Z (Yk -

Т, =       , ^k =1 --------;--10 0% .

2 il

У Z Y - ² + Z ( Y k^MOd )

I k =1

Таблица 1

Параметры моделей и критерии качества моделирования и прогнозирования при описании истории добычи нефти на С-ском месторождении

Модель		Параметры						Критерии качества
Тренд	Асимметрия	Y max , тонн	t 0 , лет от начала исследования	□ 1	□ 2	□ т	□ T1	R2	T 2 , %
Капица	Симметрия	1223726	17,19	8,25				0,9013	23,1
	Верхулст	1190619	14,36	5,29	14,47	0,51		0,9706	13,2
	Ричардс	1184633	14,46	5,42	15,18	1,51	0,12	0,9769	16,7
	Гомперц	1190020	14,51	5,41	14,29	1,64		0,9715	12,9
Хабберт	Симметрия	1189322	17,20	0,20				0,9409	41,9
	Верхулст	1142785	15,20	0,26	0,13	1,20		0,9719	16,0
	Ричардс	1120577	15,05	0,26	0,12	1,39	0,69	0,9712	14,3
	Гомперц	1122645	15,09	0,26	0,12	2,21		0,9718	14,3

Второй коэффициент Тейла (7) близок по своим значениям к известной MAPE-оценке прогноза, но обладает большей устойчивостью при оценке прогноза кривых, стремящихся к нулю [7] и, следовательно, больше подходит для оценки прогноза уровней добычи нефти на поздних стадиях жизненного цикла.

Методика оценки точности прогнозов такова (рис. 2): исходная выборка делится на две - по первой строится модель, а по второй оценивается полученный по ней прогноз. Границу окончания первой группы выберем на расстоянии t ident от времени начала выборки и исследуем показатели точности при глубине прогноза t pr . Выбор t ident может осуществляться произвольно. Поэтому для объективности исследования изучим выборки с t_peak+3 < t ident <  t_max-1 , т.е. с выбором t ident на 3 года после прохождения пика добычи нефти и, как минимум, за год до окончания известной выборки. При этом точка разделения данных на исследуемые и прогнозируемые будет смещаться. В дальнейшем проведем усреднение исследуемых параметров по всем изученным выборкам t ident. Отметим также, что в каждом случае будем сравнивать прогнозы с разным горизонтом t pr и усреднять значения T 2 по всем t ident с одинаковым t pr .

Таблица 2

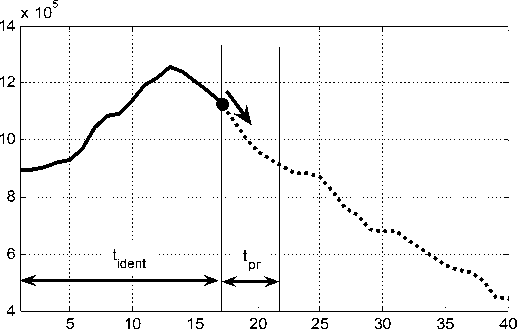
Рис. 2. Методика оценки точности прогноза

Параметры моделей и критерии качества моделирования и прогнозирования при описании истории добычи нефти на М-ском месторождении

Модель		Параметры						Критерии качества
Тренд	Асимметрия	Y max , тонн	t 0 , лет от начала исследования	O 1	О	O t	° T1	R2	T 2 , %
Капица	Симметрия	10260277	9,93	6,44				0,8170	34,2
	Верхулст	10142347	7,88	0,00	15,53	4,12		0,9888	28,5
	Ричардс	9969540	8,06	0,00	12,83	1,73	2,46	0,9896	18,1
	Гомперц	10144340	8,05	0,00	16,36	6,86		0,9921	30,8
Хабберт	Симметрия	10168008	9,95	0,28				0,8699	52,3
	Верхулст	9883405	6,80	0,57	0,12	0,08		0,9793	9,9
	Ричардс	10273082	8,06	1,53	0,13	3,38	7,00	0,9920	8,3
	Гомперц	10160900	6,96	0,56	0,14	0,11		0,9813	7,8

Из таблиц 1 и 2 видно, что для С-ского месторождения более предпочтительной с точки зрения точности прогнозирования является модель Капицы с асимметриями Гомперца, Ричардса или Верхулста, тогда как для М-ского месторождения предпочтительной является модель Хабберта с асимметрией Ричардса.

По обоим критериям – точности описания исходных данных и точности прогноза – симметричные модели жизненного цикла нефтяного месторождения выглядят существенно хуже, что подтверждают выводы [6].

Наилучшая с точки зрения выбранных критериев параметрическая модель описания добычи С-ского (модель Капицы с асимметрией Верхулста) месторождения имеет выражение ( t – номер года от начала разработки месторождения в 1958 г., добыча в т).

5,29 +

Y ( t ) =

9,18

t - 14,36

—

1 + e 0,51

( t - 14,36 ) ² +

5,29 +

9,18

t - 14,36

—

1 + e 0,51

и графически фактические, и модельные значения представлены на рисунке 3.

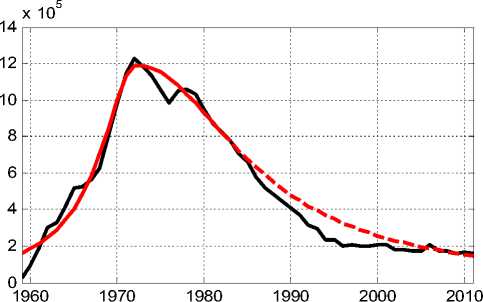
Рис. 3. Фактические и модельные значения добычи нефти на С-ском месторождении (модель Капицы с асимметрией Верхулста)

Наилучшая с точки зрения выбранных критериев параметрическая модель описания добычи М-ского (модель Хабберта с асимметрией Ричардса) месторождения имеет выражение ( t – номер года от начала разработки месторождения в 1953 г., добыча в т).

Y ( t ) = ²

1 + ch <

1,53 - 1,4

1 + e

t - 8,06

3,38

- 1/7 A

( t - 8,0 6 ) [

Фактические и модельные значения представлены на рисунке 4.

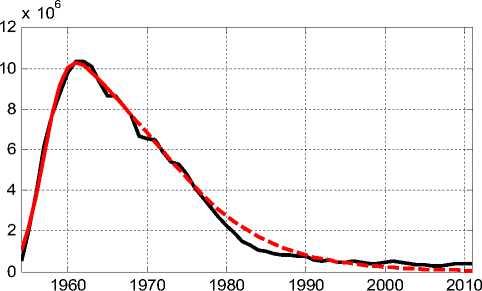
Рис. 4. Фактические и модельные значения добычи нефти на М-ском месторождении (модель Хабберта с асимметрией Ричардса)

Таким образом, в статье предложено 8 параметрических моделей, пригодных для описания динамики добычи нефти с месторождения, отличающихся от известных моделей большей гибкостью за счет использования дополнительных параметров асимметрии. Отметим, что предложенные модели достаточно универсальны из-за наличия 5-6 параметров и могут быть использованы для описания различных асимметричных колоколообразных видов динамики добычи нефти с месторождения.

Идентификация параметров предложенных моделей проведена с помощью генетического алгоритма на реальных данных 2 месторождений, и получены высокоточные параметрические модели объемов добычи. Практическое использование предложенного инструментария целесообразно для проведения комплексного исследования различной динамики добычи месторождений нефти.