Экономическая оценка истощенного месторождения нефти методом статистической базы

В условиях, когда нефтедобывающие компании слабо заинтересованы в разведке и освоении перспективных и прогнозных ресурсов углеводородов, большое народнохозяйственное значение приобретает по возможности реалистичная оценка остаточных запасов месторождений, эксплуатируемых длительное время и характеризующихся высокой степенью выработанности запасов. Месторождения нефти в процессе разработки проходят несколько стадий, отражающих меру извлечения полезного ископаемого из недр. На последней стадии для решения задачи оценки остаточных запасов нефти (способных к перемещению в продуктивном пласте) используется несколько методических приемов, начиная от простейшего, когда активные запасы рассматривают как разницу между первоначально подсчитанными объемами и накопленной добычей, и сложными, сопряженными с пересмотром геолого-промысловых параметров. Основным способом является первый. Он сильно зависит от точности первоначальных оценок запасов (которые могут отличаться от истинных значений в разы) и не может обеспечить желаемый уровень достоверности. Пересчет же геологических запасов, связанный с пересмотром промысловых параметров, представляет достаточно сложную и дорогостоя- щую операцию, и достоверности тоже не гарантирует. Эти обстоятельства обусловили поиск менее трудоемких и затратных путей решения проблемы.

Математические исследования свойств конечных совокупностей привели к разработке метода статистической базы, открывающего дополнительные возможности решения указанной проблемы. При его использовании залежь нефти рассматривается как конечная совокупность элементарных разновеликих объемов (что вполне адекватно ее физической природе как тела в ограниченном пространстве), а в качестве выборки принимаются накопленные объемы добычи нефти в эксплуатационных скважинах за фиксированные промежутки времени. Однако на практике такие данные необходимой полноты и достоверности не доступны, что потребовало альтернативного решения, а именно разработки процедур трансформации общего объема накопленной добычи нефти в случайную выборку. Эту операцию целесообразно разделить на две процедуры:

• 1)    разбиение объема накопленной добычи нефти по объекту на отдельные составляющие, выполненное случайным образом;

• 2)    генерирование из полученных элементов выборки методом Монте-Карло по одному из зако-

  нов случайного распределения, например, Парето или показательному.

  Содержательную основу метода составило утверждение о том, что если в процессе исследования конечной совокупности с неизвестным числом слагающих ее элементов полученная выборка достигает значения, которое характеризуется как состояние «исследовательской зрелости», появляется возможность без знания полного состава элементов вычислить общий объем конечной совокупности. Такая возможность была математически обоснована целым рядом исследователей [1-7] и проверена экспериментальными расчетами над известными конечными совокупностями. При извлечении из конечной совокупности выборки из N элементов в порядке s n = ( i 1 ,i ₂,..., i n ) с вероятностью, пропорциональной их размеру, и без возврата в изначальную совокупность, были получены результаты, соответствующие модели распределения на области всех перестановок элементов совокупности [1].

  Обозначим случайные варианты прописной буквой, предполагаемые – строчной. Тогда вероятность открытия элементов в порядке s _n будет иметь вид

  n /j

  P (Sn = sn\Y) = nyj( R-Z у-,),

  j=1 /

  где у = 0, R = у 1 + у2 +... + yN . С введением параметра открываемости β модель приобретает вид nj

  P(Sn = sn \Y) = пув/(R-Zув),

  j =1      /

  где у. ₀ = 0, R = у f + у ^в + ... + у ^в .

  Как показали эксперименты [2,3], между числом объектов n и суммой выражений ( 1 - exp { - X ( n ) у j }) существует связь, и при определенных обстоятельствах появляется возможность вычислить инклюзивную вероятность Р ^{ k ^{е S}n ^} = п j ( n ) того, что месторождение с номером j окажется среди первых n открытий. Она аппроксимируется как

  n j ( n ) = 1 - exp { - X ( n ) у₎ } ,          (3)

  где X(n ) - единственное решение уравнения

  ⁿ = Z ^{( 1 - ex} p ^{{ X ( n} ) у j ^}) .           ⁽⁴⁾

  j = 1

  Один из исследователей проблемы Дж. Кауфман [4] показал, что если параметр X ( n ) извес-

  
  

  Для предварительной оценки неизвестного параметра X ( n ) необходимо получить точечную оценку R по неполной выборке. Это представляет известную трудность, которая может быть преодолена выполнением оценки ожидания случайного события z_{n + 1} для (n+1) -го извлечения элемента из совокупности при условии упорядоченной выборки s n = (1,2,..., n ) :

  
  

  E [ z n J S, = (1,2,..., n )] Z --------¹----------;,

  j = 1 ^{( R -} у ^- у 2 ^- ... ^- У j - 1 )

  у 0 = 0 .                                                (6)

  Как только N становится достаточно большим, z n _{+ 1} сходится к вероятности X j ( n ) , для которой

  ^lim n Z ^exP^{{ - X} f ^{( n} ) у . ^} = ^{1 -} f ^,0 <  f < ^{11 (7)}

  
  

  где f = n/N .

  Установлено [5], что неизвестный параметр X ( n ) может быть аппроксимирован условным ожи-

  
  

  данием из выражения (7), если реальную величину R заменить ее оценкой из (5). В этом случае имеем

  
  

  выражение

  
  

  R =

  
  

  n

  
  

  1 - exp -

  
  

  —

  
  

  к

  
  
  
  

  у ^_{Б х} -1

  k = ' ^{R -} Z i = 0 у - J

  
  
  
  

  ^ , у 0 = ⁰ ,

  
  
  
  

  (8) представляющее собой уравнение, путем решения которого и получается искомая оценка.

  Как нетрудно убедиться, эффективность метода в первую очередь зависит от размера выборки, отобранной из конечной совокупности (доли J = n^N ). Как показали экспериментальные рас-

  
  

  тен априори, а элементы s _n выстроены в порядке

  1,2,..., n , то сумма всех величин объектов R может

  
  

  несмещенно и приближенно оцениваться как

  
  

  n

  R = z

  j = 1

  
  

  y j

  1 - exp{ - X ( n ) у j }

  
  
  
  

  четы авторов с совокупностями с заранее известными числом элементов и общим объемом (с 1000-кратной имитацией отбора без возвращения с перемешиванием), отклонения вычисленных показателей от исходных данных составили менее 1% при 75%-ном квантиле, а усредненный показатель по нарастающей статистической базе имеет прогностическую ценность уже при 50%-ном квантиле (рисунок). Полученные результаты свидетельствуют о более высокой достоверности оценок, получаемых по методу статистической базы, по сравнению с традиционными.

  Вычисленная величина активных запасов месторождения имеет достаточную достоверность для того, чтобы ее можно было использовать при оценке экономической эффективности проектов его эксплуатации хорошо известными методами с использованием показателей чистого дисконтированного дохода, внутренней нормы доходности и т.д. [8]. Активную (подвижную) нефть в более широком смысле, в отличие от геологических запасов, включающих подвижную и пассивную части нефти в залежах, в геолого-промысловой практике принято называть извлекаемыми запасами. Границу между извлекаемой и пассивной нефтью определяет т.н.

  
  
  

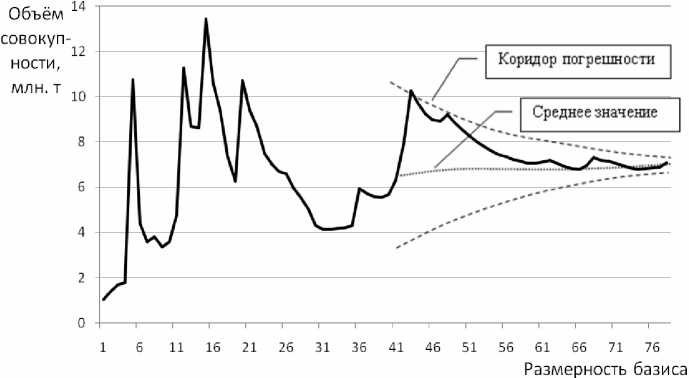
  Рис. Результаты экспериментальных расчетов по модели с известной совокупностью.