Экономичное цифровое управление в аварийном режиме стабилизации спутника на солнечно-синхронной орбите

1.    ПОСТАНОВКА ЗАДАЧИ

В [1, 2] исследован аварийный режим (АР) системы управления движением (СУД) информационного спутника на солнечно-синхронной орбите (ССО) с наведением орта к плоскости неподвижных панелей солнечных батарей (СБ) в направлении Солнца при назначении требуемого углового положения космического аппарата (КА) относительно этого направления с использованием информации о положении орта, ортогонального плоскости эклиптики. При этом устанавливаются устойчивые нелинейные угловые колебания корпуса КА из-за «конфликтующих» воздействий возмущающего гравитационного момента и управляющего момента магнитного привода (МП) на каждом витке ССО. Такой энергосберегающий аварийный режим вполне приемлем при его длительности до нескольких недель. При необходимости продолжительной (десятки месяцев) консервации КА с сохранением возможности восстановления работоспособности его СУД предлагается другой, более экономичный АР, где применяется пассивная гравитационная стабилизация спутника при ситуационном включении магнитного привода.

На рис. 1 представлены связанная с корпусом КА система координат (ССК) В (О xyz ) с ортами b _i и связанная с панелями СБ система координат P , оси которой x ^p , y ^p и z ^p в парковом положении панелей СБ (при γ ^p = 0 ) параллельны соответствующим осям ССК. Орбитальная система координат (ОСК) O (O x ^o y ^o z ^o) с ортами o _i вращается в инерциальном базисе I _ф с вектором угловой скорости Ш _о . Вводятся орт e направления на Землю и орт s направления на Солнце. В отличие от [1, 2], здесь перед выполнением АР панели СБ разворачиваются на угол γ ^p = -π /2 , а корпус КА (ССК) устанавливается в ОСК с его разворотом на угол ψ = -π /2 относительно оси O y с ортом b ₂ и наименьшим моментом инерции КА. В результате ось O x с ортом b ₁ и ось O^p y ^p с ортом n ^p совпадают по направлению с осью O z ^o ОСК и обеспечивается

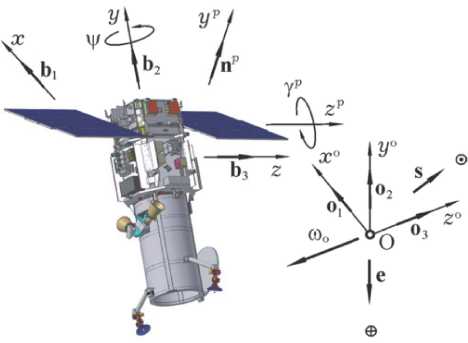
Рис. 1. Схема перехода КА в режим гравитационной стабилизации максимальный момент инерции КА по оси Ox ССК, противоположной по направлению вектору угловой скорости Юо, рис. 1.

При поступлении команды на длительную консервацию спутника выполняются следующие этапы: (i) КА переводится в орбитальную ориентацию при цифровом управлении МП; (ii) при достижении требуемой точности стабилизации КА в ОСК контур управления магнитным приводом временно выключается и спутник переходит в режим пассивной гравитационной стабилизации; (iii) для компенсации накопленных вековых возмущающих моментов, в том числе из-за влияния сил солнечного излучения, выполняется ситуационное кратковременное включение МП, что обеспечивает возвращение КА в орбитальную ориентацию с требуемой точностью. Задача состоит в (i) анализе годового перемещения орта s направления на Солнце в ОСК, (ii) разработке законов цифрового управления МП для перевода КА в орбитальную ориентацию с его последующей пассивной гравитационной стабилизацией и (iii) выполнении нелинейного анализа длительного пространственного движения КА на ССО с учетом ситуационного включения магнитного привода.

2.    МАТЕМАТИЧЕСКИЕ МОДЕЛИ

При стандартных обозначениях и отсутствии активных управляющих сил модель движения центра масс КА в инерциальном базисе имеет общеизвестный вид r = v; v = -^ r / r + ae + am + as , где ae = an + aa , am и as - векторы ускорения, обусловленные влиянием формы Земли и неравномерности распределения её массы, гравитации Луны и Солнца, соответственно. Для моделирования вектора ускорения ae используется разложение гравитационного потенциала Земли в ряд по сферическим функциям до степени n = 8 включительно с применением полиномов Лежандра и коэффициентов зональных гармоник.

В сферической системе координат (вектор r , долгота X и широта ф ) вектор ускорения а _еа зависит от r и ф , а вектор ускорения а _еа зависит также и от долготы X . Вектор ускорения a _s = ^ _s( A r /( A r )³ - r s / r S3 ) из-за влияния Солнца определяется его гравитационным параметром ц _s и расстоянием от КА до центра Солнца A r = r _s - r , где расстояние r _s от центра Земли до центра Солнца вычисляется по явным аналитическим соотношениям в функции текущей эпохи. Гравитационное влияние Луны вычисляется аналогично.

Ориентация базиса B в инерциальном базисе I _ffi определяется кватернионом

Л = ( X₀, X ) , где X = { X i } , вектором параметров Эйлера Л = { X₀ , X } , который при обозначениях C _а = cos а , S _а = sin а представляется в форме Л = { C _{ф /2} , e _e S _{ф /2} } с ортом e _e оси Эйлера и углом Ф собственного поворота, и вектором модифицированных параметров Родрига (МПР) o = {oj = е е tg( Ф /4) , который связан с кватернионом Л явными соотношениями [1]. Модель углового движения КА в базисе I _е представляется уравнениями

Л = Л о ю/ 2;

(1) J ( у )< Ъ = -юх К + М ^р + М ^m + М ^g.

Здесь K = J ( Y ) to - вектор кинетического момента (КМ) КА; to = { to i -} - вектор абсолютной угловой скорости КА, представленный в ССК O xyz ; J ( y ) = J ^o + 2 J p ( y ) — тензор инерции КА при произвольном положении панелей СБ, где тензор инерции J ^p ( y ) каждой панели зависит от угла Y = Y p ; столбец M p представляет вектор момента инерционно-гироскопических сил из-за подвижности панелей СБ [1]; M ^m = { mi ^m} - вектор управляющего механического момента магнитного привода, и наконец, вектор гравитационного момента ^{M g} = ^{{ m g }} = ⁽³M r ^{3 )} o 2 ^X J ⁽ Y ) ^o 2 .

Кватернион Л ориентации базиса O относительно базиса I _е определяется уравнением Л ⁰ = Л ⁰ ° to o / 2 , а погрешность ориентации базиса B в орбитальном базисе O - кватернионом E = Л ⁰ ° Л = ( e ₀ , e ) , вектором параметров Эйлера E = { C _ф e _/2 , e e S _ф e _/2 } , матрицей C ^e = I з - 2[ e x ] Q e , где Q e = I 3 e 0 + [ e x ] , и вектором МПР CT ^e = { ст e } = e e g ( Ф ^e / 4) . При этом вектор S to погрешности угловой скорости определяется как S to = to - C ^e to _o( t ) . При значении угла Ф ^e < п/2 вектор е = 4 ст ^e имеет представление е * 2 e e C _ф e _/2 S _ф e /2 * 5 ф с вектором угловой погрешности 5 ф = { ф i } = e e Ф ^e . Пространственный угол ф _y между ортами b ₂ и о ₂ определяется соотношением ф _y = arccos ( b ₂, о ₂ ) .

Измерение кинематических параметров углового движения КА выполняется бортовой навигационной системой [1] по сигналам спутников ГЛОНАСС/ GPS и датчиками угловой скорости в моменты времени tl _{+ 1} = t_l + Tp , l е N ₀ = [0,1,2,3...) с периодом Tp , а для измерения вектора индукции B = B b магнитного поля Земли с модулем B и ортом b в эти же моменты времени применяется магнитометр.

3.    ИЗМЕНЕНИЕ НАПРАВЛЕНИЯ НА СОЛНЦЕ В ОРБИТАЛЬНОЙ СИСТЕМЕ КООРДИНАТ

Численными методами исследовано пространственное движение центра масс спутника на ССО высотой 720 км, наклонением 98.2695 град и начальной долготой восходящего узла 51 град. Такая орбита прецессирует по долготе восходящего узла со скоростью 0.9889 град/сут, изменение её наклонения носит колебательный характер при наличии малой вековой составляющей.

Орт s направления на Солнце перемещается в ОСК по образующей поверхности конуса, ось которого направлена по оси O z ^o ОСК, а угол полураствора p S практически не изменяется в течение каждого витка орбиты, рис. 2.

Годовое изменение угла р ^ полураствора конуса представлено на рис. 3. Средние значения этого угла таковы: р * = 60 град в феврале-сентябре и р * = 65 град в октябре-январе. При указанной выше орбитальной ориентации КА ось O^p y ^p панелей СБ совпадает по направлению с осью O z ^o ОСК, поэтому здесь гарантируется среднегодовое значение основного фактора энергетического обеспечения спутника Qs = cos р * = 0.4695 .

4.    УПРАВЛЕНИЕ МАГНИТНЫМ ПРИВОДОМ

При формировании команды M _r для вектора потребного управляющего момента МП на каждом полуинтервале времени t е [ t r., t_{r + 1} ) , r е N ₀ с заданным периодом T "'¹ >>  T p выполняется дискретная фильтрация указанных выше измерений. В результате в моменты времени t_r = r TU m получаются отфильтрованные значения рассогласований £ _r по углу и 8 to _r по угловой скорости, а также отфильтрованные измерения магнитометра в _r = B _r b _r .

Для векторов x = { xi } , y = { y, } и скалярного параметра a m >  0 введем функцию

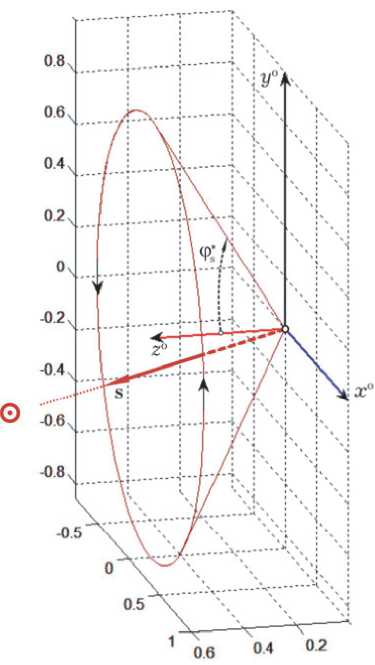
Рис. 2. Конус положений орта s у = SC(x,am) с алгоритмическим определением q = maxi | xi |; if q > am then yi = amxi I q. Эта функция ограничивает все компонеты век-m тора x по модулю параметром a , но сохраняет пропорциональность между ними.

При произвольной ориентации ССК относительно ОСК вектор дискретной команды M _r формируется по соотношению

M r = - J ( y ) SC (k _ф E r + к _и 8 to r ,a^m) , (2) где k ф ,k _ю являются постоянными коэффициентами и параметр a^m = 4к ф tg( л/8 ) = к ф П/2 . Когда вектор погрешности 8ф= { 8ф i } = е ® Ф ^е становится малым (угол Ф ^e <  3 град), вектор

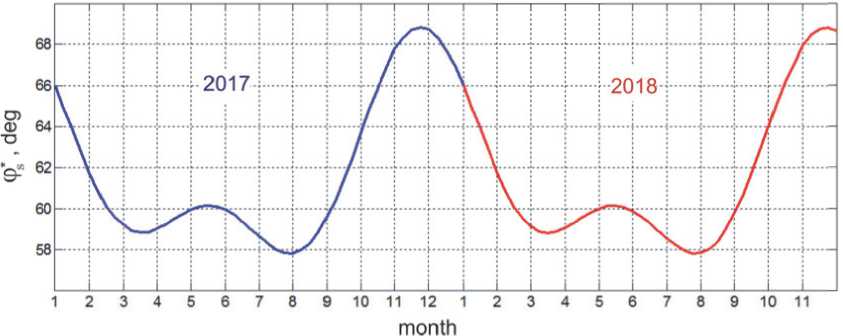
Рис. 3. Зависимость угла полураствора конуса от времени года

дискретной команды Mr вычисляется в виде gr+1 = Ьф gr + Сф е r;

М r = - J ( y ) SC (k ф g r + _Р ф £ r ,a^m), где Ь ф ,c ф ,Р ф и k ф являются постоянными параметрами.

При цифровом управлении электромагнитным моментом (ЭММ) Lr = {lir} магнитного привода сначала определяется вектор потребной вариации импульса AIm = TmMr команды механического момента. Этот импульс пред-m mb       m ставляется в виде Alr = Alr + br(Alr ,br), где Almb = br X (Alm xbr) назначается с условием (AImm,br) = 0. Далее вектор Almb = AImbim mb           m с модулем AIr и ортом ir используется при формировании цифрового управления ЭММ Lr = {lir} на периоде T™ : определяется взаимная ориентация ортов br и irm в ССК, если | (br, imm) | > cs = 1/^2, то на текущем периоде дискретности МП не включается, иначе вычисляется вектор ЭММ

L r = SC (( A I m ^b/ T ; ^m)( b r x i m )/ В r ,l^m ) (4) с компонентами | l_ir | <  l^m , который фиксируется на полуинтервале времени t е [ t r , t_{r + 1} ) . Вектор механического момента МП M ^m в (1) формируется V t е [ t r , t_{r + 1} ) по соотношению

М ^m( t ) = { m ™ (t )} = - L r x B ( t ) . (5)

5.    АНАЛИЗ УГЛОВОГО ДВИЖЕНИЯ КА

Исследовано угловое движение КА на указанной ССО высотой 720 км, когда спутник имеет массу 6500 кг и диагональные элементы его тензора инерции равны 11450, 7150 и 9450 кг м², период измерения Tp = 1 с, в соотношениях (2) - (5) период управления МП Tu m = 16 с и параметр ограничения компонентов вектора ЭММ магнитного привода l^m = 300 А м². Компьютерная имитация выполнена при нелинейном анализе перехода КА из ориентации в подвижной солнечно-эклиптической системы координат, которая формируется на борту КА по фактическим данным о направлении на Солнце и положении оси, ортогональной плоскости эклиптики [1,2], в режим орбитальной ориентации при начальном значении угла Ф ^e = 11 град и соответствующем малом значении вектора начальной угловой скорости в инерциальном базисе I _е . На рис. 4 - 6 приведены кинематические параметры динамического процесса при таком переходе КА в орбитальную ориентацию в течение П = 4 витков его орбитального полёта.

На рис. 7 и 8 представлены изменения компонентов вектора угловой погрешности 5ф = { 5ф i } и угла ф y между ортами b ₂ и о ₂ , начиная с пятого витка по 145 виток полёта спут-

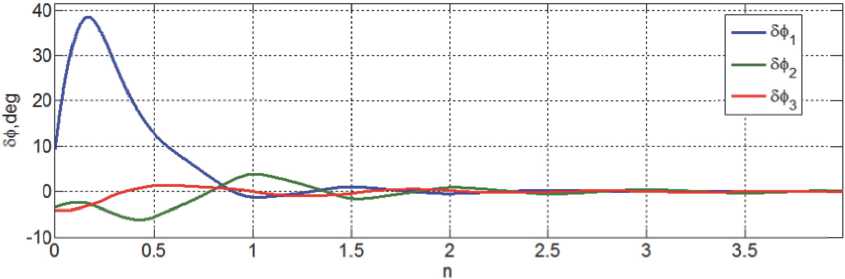
Рис. 4. Угловые погрешности при переходе КА в орбитальную ориентацию

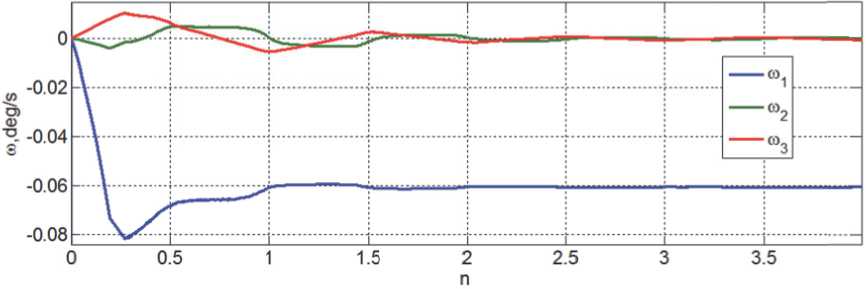
Рис. 5. Угловые скорости КА при переходе в орбитальную ориентацию

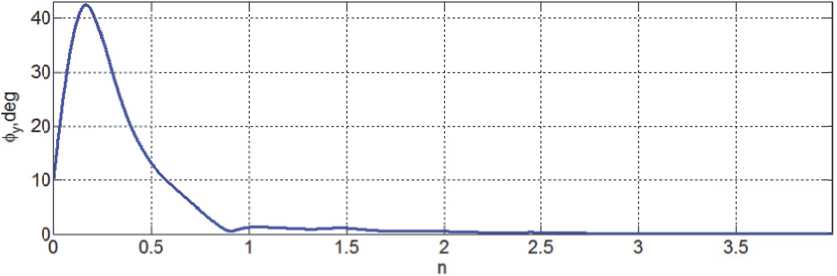
Рис. 6. Пространственный угол ориентации орта b ₂ относительно орта o ₂ местной вертикали

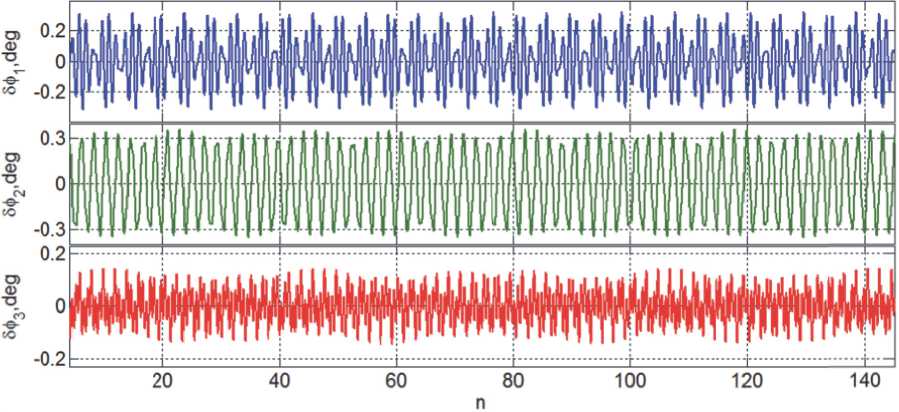
Рис. 7. Компоненты вектора угловой погрешности при гравитационной стабилизации КА

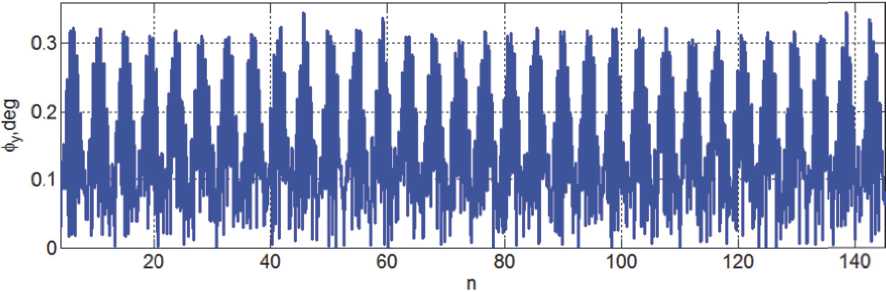
Рис. 8. Пространственный угол ориентации орта b ₂ относительно местной вертикали

ника (10 суток), а на рис. 9 - изменения угла ф y на последних 10 витках. Гравитационные возмущения от Луны и Солнца приводят к «модуляции амплитуды» пространственных угловых колебаний КА с месячным и годовым периодами, а усреднённая скорость изменения такой «амплитуды» по модулю не превышает 0.015 град/сут.

Компьютерная имитация показала, что в силу отсутствия какого-либо физического демпфирования в режиме гравитационной стабилизации спутника «амплитуда» его нелинейных угловых колебаний относительно ОСК в течение месяца может возрасти до значения Фe = 0.85 град. При анализе движения КА на ССО в долговременном экономичном аварийном режиме необходимо также учитывать влияние сил давления солнечного излучения, где требуется информация о форме, размерах и отражательных свойств конструкции спутника. Численные расчеты показали, что при пассивной гравитационной стабилизации спутника влияние сил давления солнечного излучения в течение месяца

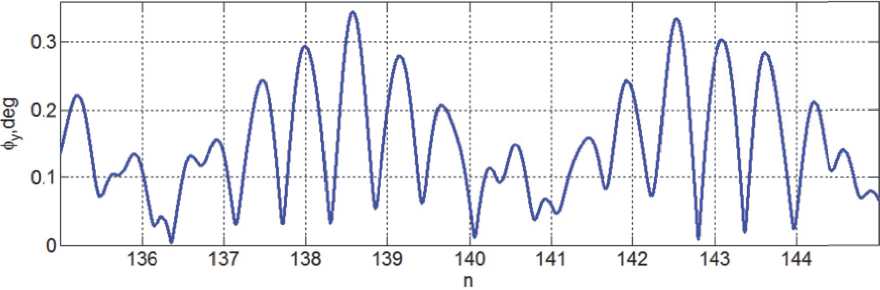
Рис. 9. Угол ориентации орта b ₂ относительно местной вертикали на последних 10 витках

может привести к дополнительному возрастанию «амплитуды» его нелинейных угловых колебаний относительно ОСК до значения ф ^e = 1.27 град. Текущая оценка «амплитуды» угловых колебаний КА регулярно выполняется на основе фильтрации измерений бортовой навигационной системы по сигналам спутников ГЛОНАСС/ GPS. При превышении такой оценки заданного значения (например, ф ^e = 1.5 град) включается закон цифрового управления МП (3), который в течение трёх витков орбитального полета гарантированно обеспечивает возвращение КА в орбитальную ориентацию с требуемой точностью.

ЗАКЛЮЧЕНИЕ

Разработаны алгоритмы экономичного управления ориентацией информационного спутника на ССО в долговременном аварийном режиме. Предложена и исследована новая схема выполнения аварийного режима, где существенно используются свойства солнечно-синхронной орбиты при сочетании пассивной гравитационной стабилизации и ситуационного активного цифрового управления ориентацией спутника с помощью магнитного привода. Приведены результаты компьютерной имитации аварийной ориентации спутника землеобзора на солнечносинхронной орбите высотой 720 км.