Экономичный обогрев помещения как задача оптимального управления

Проблемы управления режимами теплоснабжения и их оптимизации (соблюдения нормативных режимов, экономии затрат и т.п.) играют важную роль в настоящее время и, видимо, будут играть еще большую роль в будущем. По мнению виднейшего современного футуролога Артура Кларка, в будущем все расчеты должны будут измеряться единицами затрат тепловой энергии ( кВтч ) , то есть тепло станет единой «мировой валютой»!

Естественно, все мало-мальски обоснованные рекомендации по режимам теплоснабжения должны основываться на математических моделях рассматриваемых процессов. К сожалению, сейчас наблюдается огромный разрыв между практически применяемыми простейшими инженерными и статистическими моделями описания (и анализа) тепловых процессов и высоко научными (но мало применимыми на практике) моделями тепловых полей, требующих использования сложных уравнений математической физики. Этот разрыв в какой-то степени заполняет предлагаемая статья.

Производство тепловой энергии для теплоснабжения производственных, администра- тивных и жилых зданий обеспечивается от ТЭЦ, районных или местных котельных. Во всех отмеченных случаях возникает задача оптимизации затрат на транспортировку тепловой энергии. В данной статье приводятся некоторые примеры математического моделирования процесса транспортировки тепловой энергии по теплотрассам прямой и обратной подачи на основе разработанных в [1] моделей.

Система теплоснабжения представляет собой сложную систему с многообразием составляющих ее элементов, в которых протекают различные по физической сущности процессы поглощения, превращения и переноса теплоты. Рассмотрим систему теплоснабжения зданий как множество объектов с набором связей и свойств между ними. Принципиальной особенностью этой системы является то, что система теплоснабжения зданий представляет собой не простое суммирование объектов системы, а особое их соединение, придающее всей системе в целом новые качества, отсутствующие у каждого из ее элементов [1].

При этом объекты функционируют как единое целое, каждый объект работает как составляющая часть системы ради достижения единой цели. В настоящее время для построения и реализации математических моделей сложных технических систем используется методология системного подхо-да.Обобщенная постановка данной задачи формулируется следующим образом: требуется минимизировать эксплуатационные расходы и капитальные вложения в систему теплотрасс прямой и обратной подачи при обеспечении необходимой температуры теплоносителя на вводе в обогреваемое помещение (связанной с соблюдением температурного режима обогреваемого помещения).

Основная сложность в решении данной задачи - моделирование переходных и стационарных режимов работы теплотрасс. Полная постановка задачи оптимизации систем теплового снабжения (СТС) требует комплексного рассмотрения работы СТС в целом, включающей котельную (ТЭЦ), теплотрассы прямой и обратной подачи, обогреваемое помещение. Однако, отдельное исследование тепловых процессов в трубопроводах представляет самостоятельный интерес (проверка адекватности всех элементов модели, вопросы оптимизации затрат на транспортировку тепловой энергии по теплотрассе) и необходимо для дальнейшего моделирования системы в целом.

Естественно, что «стратегически наилучшим» вариантом решения данной проблемы является сокращение затрат как на транспортировку тепловой энергии, так и на сооружение теплотрасс за счет установки местных котельных. Такие компактные котельные малой мощности и с высоким КПД выпускаются в настоящее время целым рядом отечественных и зарубежных производителей. Однако, для подавляющего большинства потребителей тепловой энергии переход на производство тепловой энергии на собственных (встроенных) миникотельных представляется проблематичным по целому ряду объективных причин (в первую очередь организационно-экономических). Поэтому вопросы оптимизации затрат на передачу тепловой энергии по теплотрассам являются актуальными и требуют своего разрешения.

Одним из путей значительного снижения затрат тепловой энергии на поддержание требуемого согласно СНиП 2.04.05-91* темпе- ратурного режима в административных зданиях является снижение температуры в ночное время и в нерабочие дни. Получаемый при периодическом охлаждении помещения экономический эффект можно определить из соотношения tp

^z=с о Ke (t) - Qp (t )d, (1) о где: c0 - стоимость тепловой энергии, руб/(кВт*час); Q(t) - потребляемая тепловая энергия без учета регулирования, кВт*час; Qр (t) — тепловая энергия потребляемая с учетом регулирования, кВт*час; tp - время регулирования, час.

Важным звеном в решении задачи периодического снижения температуры является минимизация расхода тепловой энергии на «на-топ» (переходной режим «ночь-день») и на охлаждение (переходной режим «день-ночь») помещения.

Математическая модель для анализа процессов эффективности теплового снабжения в режиме «натопа» приведена в [2]. В качестве начальных условий здесь выступают начальная Т 0 и конечная Т 1 температуры в помещении, а также время 1 1 , за которое совершается переход от Т 0 к Т 1 . Управляющим параметром является температура обогревателя Т р , и задача оптимального управления сводится к минимизации потребления энергоресурсов, пропорционального величине T p ^ min.

Это - стандартная задача линейного оптимального управления, и ее решение можно найти с помощью принципа максимума описанного в [3].

Методика расчетов оптимального управления переходными режимами при «натопе» помещения

Как показали проведенные по предложенной модели расчеты характер протекания переходного процесса при «натопе» помещения полностью определяется начальными условиями и не зависит от момента подачи управляющего воздействия u=1 . Следовательно, для проведения расчета необходимо:

• •    задать интервал времени t 1 , достаточный для перевода системы отопления из ночного режима в дневной при включении системы отопления на максимальную допустимую мощность;

• •    задать шаг изменения времени таким, чтобы интервал времени t₁ разбить на 15-20 равных отрезков;

• •    провести расчет температуры в отапливаемом помещении в переходном режиме «ночь-день»;

• •    определить интервал времени, необходимый для повышения температуры в помещении от Т₀ до Т₁ (в случае необходимости уменьшить шаг изменения времени, для более точного вычисления времени переходного процесса);

• •    отступив от начала рабочей смены на интервал времени перевода системы отопления из ночного режима в дневной, получим момент включения системы отопления на максимальную мощность для «натопа» помещения к началу рабочей смены.

•

Практическое применение разработанной методики

В качестве примера рассчитаем возможную экономию тепловой энергии за счет рациональной организации «натопа» помещения с Т 0 = 14 ⁰ С до Т 1 = 20 ⁰ С . Характеристики помещения и ограждающих конструкций: Т с = -20 ⁰ С ; S p =1,5 м ²; S CT = 10 м ²; V = 50 м³; λ CT = 0,41

зультаты соответствующих расчетов приведены в таблице 1.

На рис. 1 приведена диаграмма зависимости времени на перевод системы отопления из ночного режима отопления в дневной при ступенчатом изменении температуры обогревателя от T p ( T 1 ) = 47,096 ⁰С до T p = 95 ⁰С с шагом 5 ⁰ С .

Таблица 1 – Результаты моделирования затрат тепловой энергии на «натоп» помещения

Тр? 0С	Время "натопа" мин	Расход тепла, КДж	Снижение расхода тепла, %
47	180	3764,936	100
50	80	3538,548	93,986836
55	44	3462,082	91,955835
60	30,8	3435,791	91,257523
65	23,8	3420,269	90,845246
70	19,4	3397,433	90,238702
75	16,4	3387,25	89,968233
80	14,2	3383,682	89,873464
85	12,6	3370,547	89,524587
90	11,2	3369,668	89,50124
95	10,2	3366,054	89,405249

Вт/ ( м*⁰С ); δ

λ p = 8,07 Вт/(м*0С); ρvz δp

=1,205 кг/м³, c_pvz =1005 Дж/ ( кг*⁰С ).

Значения температуры обогревателя для поддержания стационарного режима в дневное и ночное время соответственно составили: Tp(T1)= 47,096 0С, Tp(T0)= 37,032 0С.

Для проведения расчетов определим так называемый «полигон» для «натопа» помещения, который будет равен максимальному времени разогрева помещения за счет скачкообразного увеличения температуры радиатора от T p ( T 0 )= 37,032 ⁰С до T p (T 1 )= 47,096 ⁰С. При этом температура воздуха в помещении повысится от Т 0 = 14 ⁰С до Т 1 = 20 ⁰С за 180 мин. В дальнейшем значение T_p ( T ₁) будем ступенчато повышать с шагом в пять градусов Цельсия. Время «натопа» помещения при этом будет уменьшаться. Расход же тепловой энергии будем проводить на интервале 180 минут: вначале от поддержания T p ( T 0 )= 37,032 ⁰ С , затем от реального изменения температуры в помещении при скачкообразном увеличении T_p ( T ₁). Ре-

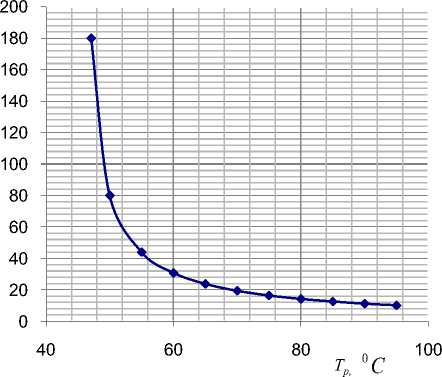
Рисунок 1 – Зависимость времени «натопа» от температуры обогревателя

На рис. 2 приведены результаты расчетов затрат тепловой энергии на перевод системы отопления в режиме «ночь-день» в зависимости от температуры обогревателя.

Как видно на рисунках с повышением температуры обогревателя снижаются как вре- мя затрачиваемое на «натоп» помещения, так и необходимые затраты тепловой энергии (расчетное подтверждение принципа максимума Понтрягина-Беллмана).

В последнем столбце таблицы приведены относительные величины уменьшения затрат тепла в интервале времени продолжительностью в 180 минут за счет последовательного приближения к принципу максимума.

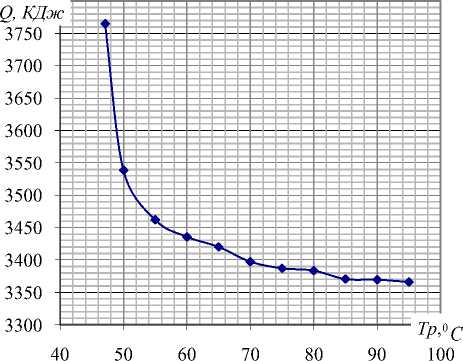
Рисунок 2 – Зависимость расхода тепла на «на-топ» от температуры обогревателя прибора с обогреваемым помещением и окружающей средой. Уравнение теплового баланса в этом случае представляет дифференциальное уравнение первого порядка для средней температуры T в помещении, где управляющим фактором является средняя температура обогревателя (радиатора) T .

При очевидной неполноте предложенной модели (температура отопительного прибора не является независимым фактором, она определяется режимом работы источника и потерями в теплотрассах), целесообразно проанализировать физическую сущность процессов, происходящих при теплоснабжении отдельного помещения в стационарном и переходных режимах. Рассмотрение данного вопроса позволит прояснить природу физических процессов, происходящих в СТС, оценить доли различных составляющих в уравнении теплового баланса.

Как видно уменьшение затрат тепла за счет использования системы отопления на максимальной мощности в режиме «натопа» составило около 400 КДж или 10,6 % от ее начального значения при «натопе» путем задания T p ( T 1 ) = 47,096 ⁰С. Очевидно, что проведенный расчетный эксперимент можно считать практическим подтверждением принципа максимума Понтрягина-Беллмана.

Важной особенностью является необходимость системного анализа, учета теплового взаимодействия разных элементов системы теплоснабжения. В [1] описана модель системы «источник – теплотрасса прямой подачи – отопительный прибор – помещение – теплотрасса обратной подачи», представляющая систему пяти линейных обыкновенных дифференциальных уравнений. В соответствии с методологическим принципом последовательного анализа усложняющихся моделей и для выявления основных закономерностей распределения тепла и затрат в [1] рассмотрен важнейший элемент этой системы: взаимодействие отопительного