Экономико-математическая модель выбора параметров трубопроводных систем снабжения мазутом

В исследовании [1] представлен углубленный анализ структуры затрат при планировании мер по повышению энергоэффективности в жилом секторе. Высотные здания, которые в основном работают на природном газе и легком дистиллятном мазуте, демонстрируют высокую рентабельность за счет модернизации. Рассматривая результаты финансовой оценки, наиболее значительные выгоды в основном связаны со сценарием модернизации, который учитывает улучшение изоляции внешних стен, остекление окон и повышение эффективности работы системы отопления.

В работе [2] исследуется производительность системы воздушного теплового насоса с регулируемой скоростью на основе компрессора, являющейся альтернативой нефтяным и газовым котлам. Оценка проводилась с учетом влияния режима работы системы управления и температуры теплоснабжения.

Прием, хранение, подготовка и подача необходимого количества мазута для его сжигания в топках котлов, является одной из энергоемких технологических подсистем тепловых электростанций и котельных [3]. Проектирование новых технологических трубопроводов и модернизация существующих трубопроводных систем для транспортировки мазута предполагает проведение гидравлических расчетов. Общепринятым является гидравлический расчет трубопроводов, основанный на уравнении непрерывности потока и уравнении Бернулли для реальной вязкой жидкости, в котором учитываются потери давления из-за трения и преодоления местных сопротивлений трубопровода. При таком подходе гидравлический расчет является многовариантной задачей, поскольку существует бесконечное количество комбинаций параметров диаметр трубопровода – перепад давления, которые не равны как с экономической, так и с технической точек зрения. Исследование литературных источников показало целесообразность проведения гидравлического расчета трубопроводно-проводных линий по техникоэкономическим показателям [3]. В качестве критерия оптимизации технологических трубопроводов предложены общие годовые затраты на создание и эксплуатацию трубопровода, которые представляют собой линейную суперпозицию капитальных и эксплуатационных затрат. Предложены расчетные соотношения для определения оптимального диаметра трубопровода из условия минимальных совокупных годовых затрат на его создание и эксплуатацию с учетом текущих цен и тарифов на трубопровод и электроэнергию, трассировки трубопровода, условий его эксплуатации, а также свойств транспортируемой среды. На примере гидравлической установки для перекачки мазута были проведены вычислительные эксперименты для оценки влияния диаметра трубопровода на его технико-экономические показатели и определения оптимальных параметров мазутопровода.

Масляное отопление по-прежнему используется в районах, не охваченных метановой сетью. Отопление на мазуте становится все более дорогостоящим, требует частых операций по заправке резервуаров [4].

Улучшение развития цепочки поставок ископаемого топлива является эффективным способом снижения затрат и выбросов углекислого газа. В статье [5] анализируется развитие инфраструктуры системы доставки нефтепродуктов. Предложена математическая модель транспортировки и хранения.

Вспомогательные котлы на борту теплоходов являются предметом постоянных исследований. Пар вырабатывается для нагрева топлива и работы турбин. Проведен анализ судового котла, работающего на мазуте [6]. Напорная струйная горелка имеет КПД 70-80%. Были рассчитаны и определены потери эксергии в камере сгорания.

Нефтяные компании производят различные продукты на нефтеперерабатывающих заводах и часто транспортируют их по трубопроводам. Трубопроводы позволяют перемещать огромное количество нефтепродуктов [7]. Планы доставки определяют последовательность операций перекачки. В работе [7] представлена система моделирования дискретных событий, которая помогает проверять расписание в сложных разветвленных трубопроводных сетях.

Одним из видов объемных насосов является шестеренный насос, предназначенный для перекачки нефти и нефтепродуктов, обладающих смазывающей способностью, без механических примесей и не вызывающих коррозии рабочих органов насоса, а также для перекачки легковесных жидкостей и дизельного топлива. Авторами работы [8] представлена модернизированная конструкция шестеренного насоса.

В статье [9] представлена физико-математическая модель аварийных ситуаций на предприятии по перевалке мазута в городе Мурманске. Описано технологическое оборудование и результаты расчетов рисков при транспортировке, перекачке и хранении топлива в случае полной и частичной разгерметизации резервуаров. Показаны риски в наиболее сложных чрезвычайных ситуациях, возможный радиус ущерба.

В статье [10] сообщается о новой гибридной системе отопления. Система состояла из тепловых насосов из подземных источников для основного отопления и существующего подогревателя мазута для пикового нагрева. Эффективность системы, включая экономию мазута и энергии, была оценена на основе измерений в течение отопительного периода с ноября 2014 года по май 2015 года. Результаты показывают, что по сравнению с использованием только существующего мазутного нагревателя для обогрева теплицы, система может сэкономить 74,4% мазута и 22,8% энергии. В целях дальнейшего повышения производительности были улучшены управление системой подачи горячего воздуха в помещении и местная теплоизоляция теплицы. Оценка эффективности, основанная на измерениях с ноября 2015 года по май 2016 года, показывает, что улучшенная система может сэкономить 88,0% мазута и 35,9% энергии.

Материалы и методы

Большое количество трудов посвящено совершенствованию мазутного хозяйства, в частности – перекачивания мазут [11,12]. Мазут обладает большой вязкостью, сильно зависящей от температуры. Так при 43°C кинематическая вязкость мазута марки М100 составляет 2000 сСт, а при 80°C она падает почти до 150 сСт. Мазут марки М100 при температурах выше 31°C имеет свойства ньютоновской жидкости.

При невысоких температурах для перекачивания мазута используют объемные насосы. Шестеренные насосы (ШН) наиболее распространены для подачи и перекачки мазута. ШН могут работать в оба направления; для предотвращения избыточного давления, насосы могут комплектоваться предохранительными клапанами; для предотвращения застывания продукта, насос может быть укомплектован нагревательными элементами.

В таблице 1 приведены характеристики ШН производства АО «Корвет»3. ШН предназначены для перекачивания нефтепродуктов, кинематическая вязкость которых находится в диапазоне от 18 до 3500 мм2/с (сСт).

Рекомендуется уменьшать ЧВР ШН с увеличением вязкости мазута в соответствии с таблицей 2.

Таблица 1 – Характеристики ШН производства АО «Корвет»

Марка насоса	Подача, м3/час	Вязкость, сСт	Частота, об/мин	Мощность, кВт (при перепаде давления, кПа)
				200	300	400	600	1000	1500
НШ-4	4	110	1500	0,75	1,1	1,5	2,2	3	4
НШ-5	5	110	1500	1,1	1,5	2,2	3	4	5,5
НШ-10	10	220	1000	3	3	4	5,5	7,5	11
НШ-20	20	220	1000	4	5,5	7,5	11	22	30
НШ-40	40	220	1000	7,5	11	15	22	30	45

Таблица 2 – Частота вращения (ЧВР) ШН с увеличением вязкости мазута

Вязкость мазута, сСт	110	220	1100	2200	11000	22000
ЧВР, об/мин	1500	1000	800	500	300	200

Важную роль в совершенствовании мазутного хозяйства имеют экономические показатели [13]. Именно на таких показателях основан выбор оптимального внутреннего диаметра трубопровода D : его увеличение приводит к снижению энергоемкости при эксплуатации, но увеличению материалоемкости при строительстве. Задача успешно решается для перекачивания маловязких жидкостей в турбулентном режиме (см., например, [14-16] и библ. в них).

Впервые задача определения оптимального диаметра трубопровода при ламинарном течении жидкости была решена в [17] без учета потерь в местных гидравлических сопротивлениях. В [18] динамическая вязкость раствора 0,25 Па·с (ошибочно указана единица измерения м²/с), гидравлические потери в местных сопротивлениях учитываются простым умножением на коэффициент 1,1 потерь по длине трубопровода, т.е. просто добавляется 10%. В результате получается, что необходимая мощность насоса для ламинарного потока зависит от диаметра трубопровода как 1/ D ⁴.

В [19] была предпринята попытка строго учесть потери энергии в местных гидравлических сопротивлениях при ламинарном течении с помощью известной формулы ΔpM = 0,5·ζM·ρW2/g, где ρ – плотность жидкости, g – ускорение свободного падения, W – скорость жидкости. Однако коэффициенты местных потерь ζM взяты постоянные, не зависящие от числа Рейнольдса, как при турбулентном режиме течения.

Затраты на изготовление и эксплуатацию трубопровода можно представить следующим образом [14-16, 18, 19]:

C = C B + C E = ( C BO + c B D·L ) + ( C EO + c E ·A E ), (1)

где   CB – капитальные затраты, приведенные к одному году;

C E – годовые эксплуатационные затраты;

C BO , C EO – затраты, не зависящие от диаметра, капитальные и эксплуатационные, соответственно;

c E – тариф на электроэнергию;

c B – эмпирический коэффициент, определяемый по прайс-листам (руб./м²);

L – длина трубопровода;

A E – работа, затраченная электродвигателем насоса за время T .

A E = N E · T = N · T/ η E .              (2)

где   η E – КПД электродвигателя;

N – затраченная мощность ШН.

Заметим, что линейная зависимость стоимости от внутреннего диаметра характерна для стальных труб. Для отыскания значения D, при котором C достигает минимума, приравнивают к нулю производную целевой функции по диаметру:

Pr ( D ) ≡ dC/dD = c B ·L + c E ( T/ η E )· dN/dD . (3)

По (3) необходимо найти зависимость затраченной мощности ШН от внутреннего диаметра трубопровода D . Полагаем, что вязкость жидкости велика, и реализуется ламинарный режим течения.

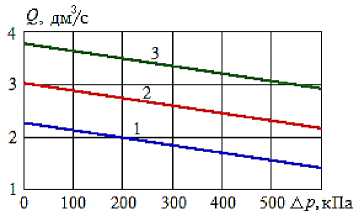
Рисунок 2 – Связь между перепадом давления и подачей насоса Ш40-4 при различных значениях ЧВ : 1 – n = 6 с^-1, 2 – n = 8 с^-1, 3 – n = 10 с^-1

Результаты исследования

В [20] для аппроксимации зависимостей подачи Q и мощности N ШН от перепада давления используются формулы:

Q = Q 0 – α · Δ p , (4)

N = N 0 + β · Δ p , (5) где Q 0 , N 0 – подача и затраченная мощность при Δ p = 0, соответственно.

Анализ результатов испытаний агрегатов Ливгидромаш⁴ показал, что зависимость от частоты вращения (ЧВ) n у ШН, как у одновинтовых насосов, может быть представлена в следующем виде:

Q = V 1 ·( n – a 1 ·Δ p ), (6)

N = ( A 1 + a 2 · Δ p )· n , (7) где V 1 , A 1 – объем жидкости и механическая работа ШН за один оборот при Δ p = 0.

В качестве примера рассмотрим агрегат Ливгидромаш Ш40-4. Экспериментальные значения показаны точками на рис. 1 при вязкости мазута 1800 сСт, ЧВ n = 980 об/мин (16,3 с^-1).

кВт

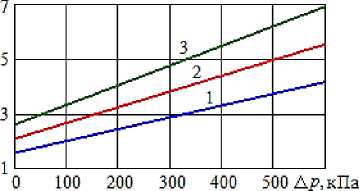
Рисунок 3 – Связь между перепадом давления и затраченной мощностью насоса Ш40-4 при различных значениях ЧВ : 1 – n = 6 с^-1, 2 – n = 8 с^-1, 3 – n = 10 с^-1

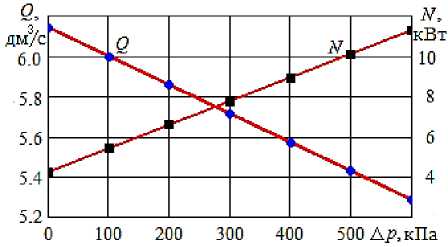
Рисунок 1 – Рабочие характеристики агрегата Ливгидромаш Ш40-4 : точки – экспериментальные данные; линии – результаты расчета по формулам (6), (7)

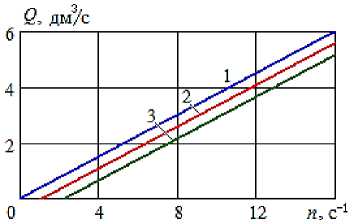
Рисунок 4 – Зависимость подачи насоса Ш40-4 от ЧВ при различных значениях перепада давления :

Характеристики по формулам (6), (7) были пересчитаны на разные значения ЧВ и перепада давления (рис. 2-4).

Методом наименьших квадратов были найдены значения размерных коэффициентов в формулах (6), (7): V 1 ·= 0,3761 дм³; a 1 ·= 3,704·10^{– 3} (кПа·с)^–1; A 1 = 0,259 кДж; a 2 = 7,195·10^–4 кДж/кПа.

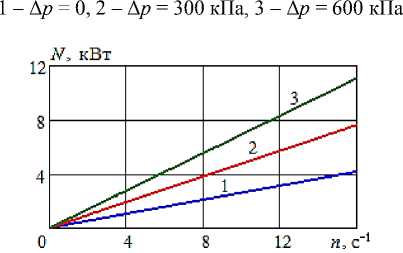
Рисунок 5 – Зависимость затраченной мощности насоса Ш40-4 от ЧВ при различных значениях перепада давления : 1 – Δ p = 0, 2 – Δ p = 300 кПа, 3 – Δ p = 600 кПа

При большой вязкости жидкости характеристику трубопровода (зависимость гидравлических потерь давления от расхода) можно записать в виде

P T = p c + (y o / D ³ + Y 1 / D 4 ) Q , (8) где p c - статическое давление, обусловленное разностью уровней и давлений в исходном (И) и конечном (К) технологическом резервуаре:

p c = р к - Р И + ( Н к — Н и )/р g . (9)

Размерные коэффициенты в формуле (8) определяются гидравлическим сопротивлением трубопровода:

Y o = 2pvLЛ i /п, у 1 = 128pv L In, (10) где v - коэффициент кинематической вязкости;

• L - длина трубопровода;

£Л i - сумма коэффициентов местных сопротивлений, следует из зависимости

Z m i = Л i I Re .

Для заданного трубопровода при неизменных свойствах жидкости коэффициенты у 0 и y i остаются постоянными.

На рис. 6 показан примерный вид характеристик трубопровода при двух значениях диаметра: 1 - при D i , 2 - при D 2 , причем D i >  D 2 .

Пусть диаметр равен D 1 . Прямая линия 3 - напорная характеристика ШН при такой ЧВ n 1 , что в рабочей точке насосной установки (А) подача равна заданной величине Q Р . Если уменьшить диаметр до значения D 2 , то рабочей точкой станет (В), так как возрастут гидравлические потери. При этом уменьшится расход жидкости. Чтобы расход был равен Q Р , напорная характеристика ШН (линия 4) должна проходить через точку (С). Характеристике 4 будет соответствовать другая ЧВ n 2 >  n 1 .

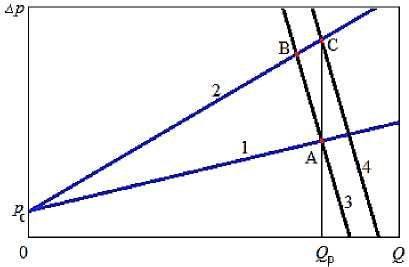
Рисунок 6 – Смещение рабочей точки при изменении диаметра трубопровода

Эти графические построения запишем в виде алгебраических уравнений и формул. В рабочей точке р т = А р . Из (6) выразим ЧВ:

n = Q p I V г+ a 1 "А р = n p + a v(p c + (у о / D ³ +^ _+у 1 / D ⁴) Q p ). (11)

Подставим (11) в (7) и выразим затраченную мощность ШН:

N = [ A 1 + a 2 (p c + (у о / D ³ + У 1 / D ⁴У Q p )] • [ n p + a 1 (p c + (у о / D ³ + У 1 / D⁴)" Q p )].       (12)

Раскроем скобки в (12) и приведем подобные члены по степеням D :

N = B 0 + B 1 D ^-3 + B 2 D -4 + B 3 D ^-6 + B 4 D ^-7 + B 5 D ^-8,

B 0 = ( A 1 + a 2 p c )•( n p + a 1 p c ), B 1 = y o Q p •[( A 1 + ... ^+ a 2 p c )• a 1 + ( n p + a 1 p c )• a 2 )], B 2 = У 1 Q p •[( A 1 + a 2 p c )• a 1 + ( n p + a 1 p c )• a 2 )], B 3 = a 1 a 2 ^(y 0 Q p )²,

B 4 = 2 a 1 a 2 у 1 У 0 ( Q p )², B 5 = a 1 a 2^1 Q p )².

Найдем производную, подставив (13) в (3):

Pr(D) = Cb L - Ce (Т/Пе)^(3B1D"4 + 4B2D-5 +_ _+6 B 3 D-7 + 7 B 4D -8 + 8 B 5 D-9).(14)

Приравняв (14) к нулю, после преобразований получим:

cbPeL/(CeT) • D9 - (3B1D5 + 4B2D4 + 6B3D2 + _+7 B 4D+8 B 5) = 0.(15)

Разделим обе части (15) на B 5 :

LcПе/(CeT B5)D9 - (3 D5B1/B5 + 4 D4B2/B5 +^ _+ 6 D2 B 3/B 5 + 7 D-B 4/B 5 + 8) = 0.(16)

Заметим, что отношение B 5 / B 4 имеет размерность длины. Примем его в качестве характерного размера задачи:

D 0 = B 5/B 4 = y1/y0 = 64 L/^Л i.(17)

Введем безразмерный диаметр трубопровода d = D / D 0 . Подставив D = D 0 d в (16), после преобразований получим уравнение:

Ф^ D ¹⁰ - (© d ⁵ + 4/3 0 d⁴ + 6 d ² + 14 d + 8) = 0,

(18) где обозначены безразмерные комплексы:

0 = 3 D 0 ⁵ B 1 / B 5 = 3 D 0 ⁴^( A 1 / a 2 + П р I a 1 + 2 p c )/(y 1 Q p ).

Ф =• c b P e LD 0 ⁹I( a 1 a 2 C e T (y 1 Q p )²).    (20)

Практическое применение

Технологии работы с мазутом постоянно совершенствуются [21]. Наиболее эффективным является его перемещение по трубопроводам. Решение алгебраического уравнения (18) дает безразмерную величину оптимального диаметра трубопровода, по которому рассчитывается размерная величина D=D 0 d и соответствующая ЧВ ШН по формуле (11).

В качестве примера выполним расчет трубопровода с насосом Ш40-4 при следующих параметрах: длина L = 50 м, сумма коэффициентов местных сопротивлений £Л i = 3290, статическое давление p c = 100 кПа, подача жидкости Q p = 5,8 дм³/с = 5,8^10^-3 м³/с. Теперь можем рассчитать коэффициенты по формуле (10): у 0 =3,717 кПаю, у 1 =3,616 кПаю^м, D 0 = у 1 /у 0 = 0,973 м.

Безразмерный комплекс, рассчитанный по формуле (19), Θ = 5,921·105. Значение второго безразмерного комплекса сильно зависит от заданного периода окупаемости и от тарифов. Сначала остановимся на стоимости рекомендуемых для перекачивания нефтепродуктов стальных бесшовных горячедеформируемых труб (ГОСТ 8732-78). Прайс-листы приводятся на Интернет-ресурсах многих компаний. В качестве примера воспользуемся прайс-листом компании «Профильмет»5 на февраль 2022 года (данные показаны точками на рис. 7).

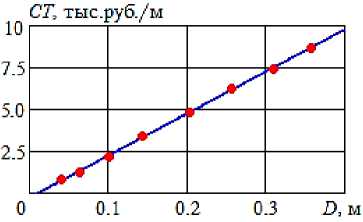
Рисунок 7 – Зависимость стоимости стальных труб от внутреннего диаметра : точки – данные прайс-листа компании «Профильмет»;

прямая – линейный тренд

Можно представить CT ( D ) = C 0 D + C 1 . Тогда производная

CTꞌ ( D ) = 25,09 тыс. руб./м² = C 0 = const. (21) c B = K · CTꞌ ( D ) = C 0 K ,         (22)

где K – коэффициент приведения капитальных затрат к одному году.

В формуле (20) необходимо задать величину c E . Тарифы на электроэнергию заметно меняются по регионам. В качестве примера воспользуемся тарифами компании⁶ для малых предприятий. Вначале возьмем наименьшее значение на январь 2022 года (Иркутскэнергосбыт) c E = 3,6067 руб./кВт·час. При K = 0,1 (срок окупаемости – 10 лет) по формуле (20) получим

Φ ≈ 2,242·109.

Решение уравнения (18) численным методом при указанных значениях безразмерных комплексов дает d = 0,210. Откуда оптимальный диаметр D = 204 мм. Из номенклатуры труб, выпускаемых российской промышленностью по ГОСТ 8732-78, выбираем 219-7 (внешний диаметр и толщина стенки в мм). Уточненный внутренний диаметр D y = 0,205 м. Перепад давления в рабочей точке насосной установки (С) по формуле (8) Δ p = p T = 114,5 кПа. Рассчитаем по (11) ЧВ n = 15,85 с^–1 ≈ 951 об/мин, которую необходимо установить на ШН, чтобы подача была равна требуемой.

С увеличением тарифов на электроэнергию будет возрастать и величина оптимального диаметра. Если взять наибольшее значение из упомянутого источника [20] (РКС-энерго, Ленинградская область) c E = 9,3654 руб./кВт·час., то получим D = 0,249 м. При этом характерный размер D 0 не изменился, так как он зависит только от параметров трубопровода.

Если уменьшить срок окупаемости (увеличить K ), то оптимальный диаметр уменьшится, как показано в табл. 3.

Таблица 3 – Влияние срока окупаемости на оптимальный диаметр

K	Φ	d	D , м	ГОСТ 873278	D y , м
0,055	1,233·109	0,238	0,231	245-7	0,231
0,10	2,242·109	0,210	0,204	219-7	0,205
0,15	3,363·109	0,193	0,188	203-7	0,189

В табл. 4 показано влияние изменения длины трубопровода. Если увеличить L , то растет порядок обоих безразмерных комплексов, возрастает характерный размер D 0 , заметно уменьшается d . При этом величина оптимального диаметра D несколько снижается.

Таблица 4 – Влияние длины трубопровода на оптимальный диаметр

L, м	Θ	Φ	D 0 , м	d	D , м
25	7,402·104	8,757·106	0,486	0,431	0,210
50	5,921·105	2,242·109	0,973	0,210	0,204
100	4,737·106	5,379·1011	1,945	0,104	0,202

Заключение

Представленный алгоритм позволяет рассчитать оптимальные диаметр труб и частоту шестеренного насоса при перекачке мазута с учетом гидравлических характеристик сети, стоимостных параметров труб и тарифов на электроэнергию.

• ⁶ Тарифы на электроэнергию для малых предприятий [Электронный ресурс]. URL:

(дата обращения: 20.02.2022).