Экономико-математическое моделирование автоматизированного проектирования трудоемкости производственнотехнологических процессов организации сложных изделий

Адаптацию метода технико-экономического и экономико-математического моделирования (описания) САПРТЭП по методологии ФСИ проведем на численном примере (элементах авиационной техники) вложения средств (затрат) с получением дохода в развитие и совершенствование названной системы.

Итак: 1. Пусть даны две пары чисел C 0 = 874, V 0 = 175 (начальная точка) и C = 103423 д.е., V = 4370 д.е. (конечная точка), определяющие соответственно связь между минимальными и максимальными величинами затрат и доходов. Считая, что в САПРТЭП поддерживается потенциальный уровень средней цены сборочных работ (и вычислительных услуг) при наличии критерия оптимальности

C

V

1 ⁰ = j x ln( к 1 x ) dx + j y ln( к ₂ y ) dy , то есть име-

C

V 0

ется система, когда устанавливается зависимость V = V ( C ) , описывающая непрерывное изменение системы при переходе от начальной к конечной точке, обеспечивающих наиболее быстрое увеличение значений численной характеристики. Далее показано, что искомая зависимость будет иметь степенной вид.

Поскольку заданы две точки, степень У и

константа А определяются однозначно: у = ln( V 0 / V )/ln ( C ₀/ C ) = 0,674, A = V ₀ / Е ₀ ^у = 1,821. Тогда из соотношения вытекает, что к ₂ = 0,0084 определяется как корень уравнения к 2 ln ^у ( к ₂ V ₀ ) = у ^У ]v 0 и далее к ₁ = у/ C ₀ ln ( к ₂ V ₀ ) = 0,002 Поэтому искомая зависимость – степенная и имеет вид V 1 = 1,821 • C ^0,674 , а соответствующие средние цены равны C 1 = V к 1 = 495,7, C ₂ = 1 к ₂ = 119,3.

Далее, 2. Пусть в добавление к нижней и верхней точкам к численному примеру по п. 1 имеется набор точек (табл. 1), где величины эффекта С и соответствующего ему вознаграждения V; V_п запланированные величины, а V₁ и V₂ – величины, рассчитанные по аппроксимирующим V зависимостям V 1 = 1,821 • C ^0,674 и V ₂ = 2,83 • C ^0,64. В этом случае не существует степенной зависимости, на графике которой лежат данные точки (рис. 1). Далее найдем степенную зависимость, которая была бы по возможности наиболее близка к набору точек, приведенных в табл. 1. Выбирая в качестве меры близости сумму квадратичных отклонений по методу наименьших квадратов, получим V 2 = 2,83 • C ^0,64. Значит, C ₀ = 874, V ₀ = 216, и далее к ₂ = 0,0067 определяется как корень уравнения к ₂ ln ^у ( к ₂ V ₀ ) = у^У Iv ₀ ( при у = 0,64 ) Наконец, к j = у C^ ₀ ln ( к ₂ V ₀ ) = 0,002 , а соответствующие средние цены равны C 1 = ^ к 1 = 495,7 , а C ₂ = 1/ к ₂ = 150,3.

В частности, оптимальное отношение цены механосборочной и слесарной работы к цене

Таблица 1. Набор точек величины эффекта C и вознаграждения V

C Vn V1 V2 874 175 175 216 2185 372 325 388 4370 656 518 605 8740 1093 526 943 13110 1442 1086 1222 17480 1704 1318 1469 21850 1923 1532 1695 30000 2167 1897 2075 40000 2467 2303 2495 50000 2767 2677 2878 60000 3067 3027 3235 70000 3367 3359 3570 80000 3667 3674 3888 90000 3967 3978 4193 103423 4370 4370 4583 вычислительной услуги равно примерно 4,2 и 3,3 соответственно в примерах по п.п. 1 и 2. Оптимальное отношение числа сборочных работ к числу вычислительных услуг (в примере п. 1) равно примерно 2,6 и 5,6, а (в примере п. 2) равно примерно 2,9 и 6,7 при затратах С=10000 и

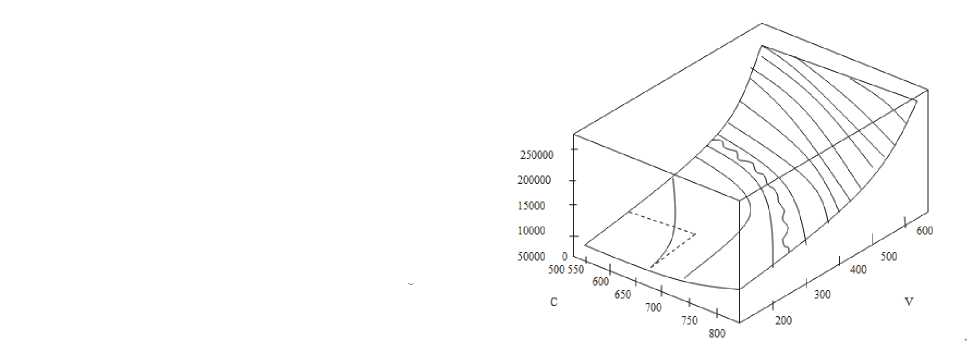
С=100000 соответственно. На рис. 1 задается множество кривых, каждая из которых определяет множество состояний САПРТЭП организации производства машиностроительного предприятия, имеющих одно и то же значение технико-экономической информационной характеристики системы. При увеличении средних значений затрат примерно в 1,5 раза и дохода в 3 раза [нижняя и верхняя линии уровня – “потенциальные возможности” САПРТЭП], ее “сложность” увеличивается примерно в 5 раз (рис. 1, б).

Таким образом, в рамках рассматриваемой модели САПРТЭП по схеме “затраты-доход” полученные результаты позволяют определять оптимальные пропорции между ее составляющими (в комплексе с промышленными АСУ и САПРТЭП) и оценивать “потенциальные возможности” состояния САПРТЭП в смысле характеристики, связанной в силу способа ее построения с множеством реализаций. Следует отметить, что хотя величины затрат, дохода (см. табл. 1), работ (сборочных), вычислительных услуг и измеряются в условных единицах (д.е.), эти данные основаны на реальном исследовании сборочного производства авиастроительного предприятия. Величины С и V_П имеют существенное значение, поскольку при их разработке явно или неявно использовались многочисленные содержательные свойства исследуемой организации производства машиностроительного предприятия как большой экономической системы при выполнении госбюджетных НИР и ОКР. При этом в примере по п.1 соответствует случай когда, по некоторым неформальным соображениям, максимальным и минимальным уровням затрат и доходов придается на авиастроительном предприятии решающее значение. В примере по п.2 отражен случай, когда все дан-

б)

а)

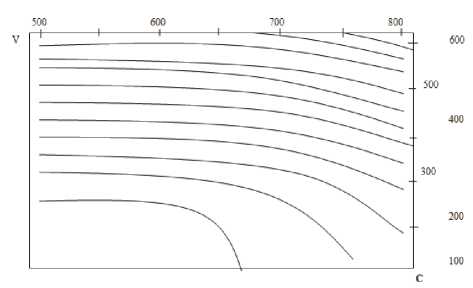
Рис. 1. Графоаналитическая интерпретация состояния системы от вложений по функциональной зависимости V = V ( С ) : а – линия уровня функции V=V(C); б – график функции V=V(C)

ные таблицы 1 имеют значение, причем значимость каждой точки учитывается в той или иной мере в зависимости от поставленной цели за счет выбора соответствующей аппроксимации.

На основании вышеизложенного, приведем соответствующее аналитическое доказательство по п.п. 1 и 2 примера.

1. По п. 1 примера доказательство вытекает из свойств интеграла, ограничений

X —■ +^ , то у ( x ) -Л X при x — +^ . Докажем.

Доказательство. Пусть заключение предложения неверно. Тогда найдется некоторое положительное 5 и последовательности X ^{— +}“ У п ^{— +}^ ^{У —} у ^{( x}„ \ ^x „ ^{— x (} у „ ^{)] та}кие, что

xn yn

1 > 5, y^ -1 > 5. xn

1                       ( 1             ^

C ( S ) < C , J ln f ( S ) dS <  ln j f ( S ) dS I , где 0                     1 0            )

f ( S ) почти всюду неотрицательная суммируемая на отрезке [0,1] функция. Покажем справедливость этого неравенства. Если f ( S ) равна нулю на некотором множестве положительной меры, то левая часть неравенства равна - ^ , и тогда неравенство верно. В противном случае для почти всех S е [ 0,1 ] в силу вогнутости логарифма получим, (касательная лежит выше графика вогнутой функции рис. 1):

ln f ( S ) < ln J f ( S ) dS

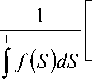
f ( S ) - J f ( S ) dS

Интегрируя это неравенство по отрезку [0,1], получим искомое неравенство, что и требовалось доказать.

• 2.    По п. 2 примера 2.1. Действительно, рассмотрим, следующее семейство функций ( e >  0): C _E ( S ) — ( 2 e ) ^{- 1} ■ C , B _E — ( 2 e ) ■ B , u f ( S ) = ( 2 e )^{- 1} ■ U , V ( S ) — ( 2 e )^{- 1} ■ V при S ₀ - E <  S <  S ₀ + E и C _E ( S ) — 0, B _E ( S ) — 0, U E ( S ) — 0, V ( S ) — 0 для остальных S е [0,1], где S ₀ - некоторое число из интервала (0,1). Тогда непосредственно проверяется, что функции этого семейства удовлетворяют соответствующим ограничениям и Ф ^[ C _e ^{( S )}> ^B _E ^{( S )}> V _E ^{( S )}> ^U _E ^{( S )] —} “ при E — 0.

• 2.2.    Сформируем и докажем два вспомогательных утверждения:

• 2.2Л . Пусть f ( t ) – монотонная положительная непрерывная функция времени, определен-

• z

ная при t > X0. Положим F(z) — J f (t) dt при x 0

• z >  X ₀ и пусть

F(z) — +^ при z — +^ .

Пусть кроме того, некоторого R >  0 при всех z > X ₀ выполняется неравенство F ( z ) < R ■ zf ( z ). Предположим далее, что каждому х однозначно сопоставлен некоторый y — y ( x ) [соответственно обратная зависимость: x — f ( у ) , причем y ( x ) —^ при X —+^ ]. Тогда, если F ( x ) ^ F [ у ( x )] при

По теореме о среднем для интеграла и в силу f (t) получим

монотонности

- |< | F (у„)-F (x„ )

" ^Х"    min [ f ^{( x}„ ⁾ , ^{f (} у „ ^)] .        ⁽²⁾

Если ^{f ( x} _n ^{)— min} [ f ^{( x} _n ⁾, ^{f (} у _п ^)] , то неравенство (2) можно переписать в виде

I Уп ^{- x}„ | <  F ^ y V^ V JLXnJ . ■ F ( x „ )

^Xn    ”      ^{F ( X}n ^{)        X}n^{f ( X}n ⁾ . ⁽³⁾

^{Если f (} y „ ^{) — min [ f ( X}„ ⁾, ^{f (} y „ ^{) ]} , ^то неравенство (2) принимает вид

I У п ^{- X}n | <  I ^{F (} У п ^{)- F ( X}n )| . ^{F (} У п ⁾ y „             ^{F (} У п ⁾        У п У ⁽ У п ⁾ . ⁽ )

Но по условию п. 2.2.1 правые части неравенства (2)-(4) стремятся к нулю при п —> +^ , что противоречит определимости от нуля левых частей этих неравенств в силу соотношений (1).

• 2. 2.2. Для функции f ( t ) — , некоторо- V ln t

• 3.    Пусть B — B ( t ), C — C ( t ) , U — U ( t ) и V — v ( t ) – решение системы и после интегрирования этих уравнений получим соотношения:

го X ₀ > 1 и построенной по ним функции F ( z ) , выполняются сделанные в п. 2.2.1 допущения. Докажем это.

Доказательство. Свойства монотонности, положительности и непрерывности функции f ( X ) очевидны, а условие F ( z )——+^ при z —— +^ выполняется в силу расходимости соответствующего интеграла. Требуемая константа R >  0 имеет место в силу непрерывности и существования конечного предела соответствующей функции, который (интеграл) вычисляется непосредственно с помощью правила Лапиталя:

F ( z )   г        f ( z )

lim —— lim / x / x =1 z—+“ zf (z) z—+“ f (z)+ zf'(z)

C2 — B2 lnB -1 в2 + R1,(5)

V2 — U2 lnU -1U2 + R2, где Ci(i = 1,2)- постоянные, определяемые по формулам

2      2            ¹2              2      2             1 2

^R1   C 0   B 0 ln ^B 0   2 B 0 , R ²    V 0    U 0 ln U 0   2 U 0 "

Используя (5)-(6) получим:

B xdx в0 x2 In x — 0,5x2 + R1

= t,

P ² = 4 z ln ( kz ) - 4 z + 4 R , (11) где R – постоянная, в силу начальных условий и уравнения (9), задается формулой:

R = ( C 0 + V ₃ ) ² - U ²ln ( kU 0 ² ) + U 0 ²"    (12)

Следовательно, из (11) вытекает, что:

U ²

J

dz

z ln( kz)- z + R

= 2 1 .

U        xdx

J I        =^ = t"

и 0 V x ² In x — 0,5 x ² + R 2

Соотношения (5)-(7) полностью задают искомое решение. Установим требуемые свойства этого решения. Из (7) вытекает, что

B xdx U xdx

B ₀ J x ² ln x - 0,5 x ² + R 1 U ₀ x ² ln x - 0,5 x ² + R ₂ (8)

Здесь нетрудно видеть, что подкоренные выражения слева и справа в (8) – возрастающие непрерывные функции переменной х при x > B0 и x > U0, равные x = B0 и x = U0 значениям C0 и V0 соответственно. Поэтому левая и правая части выражения (8) – непрерывные возрастающие функции переменных B и U. Множествами значений этих функций являются все неотрицательные числа в силу несуммируемости подынтегральных выражений в (8) (они эквивалентны функции 1/д/lnx при x ——+^ ). Следовательно соотношение (8) взаимооднозначно определяет переменные В и U, причем

В силу условия k > 1/ U 0 подкоренное выражение слева (13) возрастающая непрерывная функция и при z >  U 0 , равная при z = U 0 значению ( C ₀ + V 0 ) ². Поэтому (13) однозначно определяет (см. аналогичные рассуждения в п. 2.3) искомое решение U = U ( t ) , причем U ( t ) — +^ при t —— +^. Далее получим решение C = C"tt ) , V = V ( t ) в виде

C ( t ) = C 0 + J ln [ U ( x ) ] dx , V ( t ) = V 0 + J ln [ kU ( x ) ] dx . (14) 00

Соотношения (13)-(14) полностью задают искомое решение. Из (14) вытекает, что C ( t ) — +^ и V ( t ) — +^ при t — +~ , а в силу эквивалентности ln U Л ln ( kU ) при U — +^ получим C Л V .

• 5.    Из системы уравнений вытекает, что искомое решение C = C ( t ), V = V ( t ) определяется соотношениями:

C dx V dx

—7---x--- = t ,     ----x--- = t . (15)

C 0ln(k 1x )+ 1     Jln(k 2 x )+ 1

в — +^ и U — +^

Из (8) вытекает:

B

I

max( C 0 , B ) ) + 1

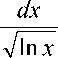
- Л

U ( B )

I

max ( C 0 , B 0 ) + 1

dx ln x

при B — +^ , где —< - знак предопределения.

Тогда, по п.п. 2.2.1 и 2.2.2, получим B Л U (при этом B — +^, U — +^) и далее отсюда и из (5)-(6) устанавливаем, кроме того, что и C Л V (при C — +^, V — +^ ), что и требовалось доказать.

4. Пусть C = C ( t ) , U = U ( t ) и V = V ( t ) -решение системы, тогда имеем соответственно:

(C + V )= ln( kU )2, ^ U2 J = 2(C + V).

Отсюда

( v

V U 2 V

= 2ln ( kU ² ) .

Полагая z = U² и делая стандартную замену z = р ( z ) из (10) после понижения порядка уравнения и последующего интегрирования получим

Рассуждая так же, как в п. 3, с применением п.п. 2.2.1 и 2.2.2 получим, что C —— ^, V —— ^ и C Л V .

Следовательно, после анализа численного примера с доказательствами по п.п. 1, 2, 3, 4 и 5, имеется основание полагать, что разработанный экономико-математический метод описания САПРТЭП в составе комплексной системы опытного производства исследуемого предприятия, логичен, жизнеспособен и функционально применим для описания технико-экономических процессов опытного производства, а также может быть кооптирован на любые комплексные автоматизированные управляющие системы отрасли машиностроения и электронного приборостроения страны.

На основании вышеизложенного, необходимо отметить, что:

1. Существующие классические методы технико-экономического и экономико-математического моделирования производственно-технологических и организационных процессов организации производства с использованием САПРТЭП обеспечивают ряд вопросов модели-

рования , но не всегда эффективны из-за относительной сложности учета ограничений , налагаемых на изменение переменных , и необходимости решения двухточечных краевых задач с использованием программных комплексов и ЭВМ, что значительно затрудняется высокой стоимостью функции расчетов.

• 2.    Проведенный анализ и исследование технико-экономических и экономико-математических методов описания САПРТЭП, а также разработанная методика технико-экономического и экономико-математического моделирования производственно-технологических и организационных процессов с использованием САПРТЭП, основанная на принципе технологии «затраты-до-ход» и «вложения-доход» по критериям функциональности и стоимости на уровне функции при верификации разработок, дают основание полагать, что разработанные методы и методика описания САПРТЭП наиболее полно обеспечивают взаимоувязку компонентов системы по функции (как полезному свойству, состоянию или действию) как с позиции технико-экономического и экономико-математического моделирования, так и математического интерпретирования и технико-экономического описания процессов организации производства технических систем.

• 3.    Использование системы вложений по методике Канбан – «затраты-доход» и «вложения-

• доход», позволяет уяснить принцип «затратности» любой исследовательской работы, которая может принести доход, доход весьма весомый, а может и остаться в виде затрат, без положительного экономического эффекта! Это позволяет исследователям при проведении НИР и ОКР настраиваться в направлении получения обязательного экономического эффекта разработок и экспериментов, что является положительным моментом «затратной» системы исследований.