Экранирование заряда макрочастицы в неравновесной плазме с учетом конверсии ионов

В настоящее время исследования пылевой плазмы находятся в фокусе внимания многих научных лабораторий ввиду широкой распространенности такой плазмы в природе и в плазменных приложениях [17], [18], [20]. Особый интерес представляет исследование характера экранирования электрического поля заряженных микро- и наночастиц в плазме, так как именно характером экранирования определяется как степень воздействия этих частиц на свойства плазмы, так и электростатический потенциал их взаимодействия друг с другом. Данная проблема имеет важное значение для развития теории зондовых измерений и теории пылевой или комплексной плазмы. Ранее в работах [15], [16], [22], [23] было показано, что экранирование заряда пылевой частицы в неравновесных условиях в плазме с одним доминирующим сортом ионов не описывается теорией Дебая – Хюккеля. Так, в двухкомпонентной плазме как с постоянным источником ионизации газа, так и с самостоятельной ионизацией газа, пропорциональ-

ной плотности электронов, экранирование в общем случае описывается двумя экспонентами с разными постоянными [15], [16], [22], [23].

В настоящей работе рассмотрена трехкомпонентная плазма с двумя сортами ионов аргона: Ar+ и Ar2+. Для аналитических и численных оценок так же, как и в работах [15], [16], [22], [23], выбрана модель точечного стока, учитывающая поглощение электронов и ионов частицей или зондом. Поскольку и здесь используется линеаризация исходных уравнений, модель применима лишь для случаев, допускающих такую линеаризацию. Эти исследования также важны для проблемы создания автономного источника электрической энергии с использованием радиоактивных частиц конденсированной дисперсной фазы микронных размеров [1], [12], [19]. Рабочей средой этого источника является пылевая плазма, в которой ионизация газа осуществляется частицами радиоактивного распада. Такая плазма по своим свойствам подобна плазме несамостоятельного газового разряда в газах, со- держащих пылевые частицы, об исследованиях которого сообщалось в [13].

1. АСИМПТОТИЧЕСКАЯ ТЕОРИЯ

ЭКРАНИРОВАНИЯ В ПЛАЗМЕ С ДВУМЯ СОРТАМИ ПОЛОЖИТЕЛЬНЫХ ИОНОВ

Рассмотрим экранирование в плазме, создаваемой внешним источником ионизации газа при повышенных давлениях. В качестве примера в настоящей работе рассмотрена плазма аргона, в которой достаточно однородная ионизация газа осуществляется высокоэнергетическими электронами пучка. Основные процессы, влияющие на состав такой плазмы, приведены в табл. 1.

Таблица 1

Основные процессы с участием электронов и ионов в плазме аргона с внешним источником ионизации газа

Процесс Константа скорости Использованное в настоящей работе значение константы Источник Ar + eb → Ar+ + e + eb Qion 1014 см–3с–1 [13] Ar + e → Ar+ + 2e ion 0 A+ + e ^ Ar + hv Pph 2,7 x 10-13 Te-0,75 см3/с [9] Ar+ + 2e → Ar + e P3 8,75 x 10-27 Te-4,5 см6/с [9] Ar+ + 2Ar → Ar2 +Ar k3i 3 x 10-31 см6/с [2], [14] Ar2 + e → 2Ar P2 0,85 x 10-6 (0,026/Te)0,67 см3/с [15] eb – электроны пучка, e – плазменные электроны, Te – температура электронов в эВ.

Для установления характера экранирования заряда макрочастиц в плазме с двумя сортами положительных ионов воспользуемся асимптотической теорией экранирования, развитой в работах [15], [16], [22], [23]. Поместим макрочастицу в центр сферической системы координат и положим, что макрочастица имеет сферически-симметричную форму. В дрейфово-диффузионном приближении уравнения, описывающие нестационарный процесс зарядки макрочастицы, имеют вид [7], [8]:

‘de- + divj,, = Qon + kion «« a -(^,h + P3 «„ ) «e«n - Д «e«(2 ^П^ + divjii = Qion + kion «« a -(Pph + P3 «„ ) «e«n - k* «t (1) d«„2

— + div j i 2 = k 3i n i i « a - ^p «_e«₍₂ d t

^ф = -4ne(«i 1 + «i2 - ne),(2)

где je = ke«e V ф - De Vne , ji1 = - k1 1 «i1V Ф - Di1V nil, ji2 = - P 2 «i2V Ф - Di2V «i2, где kc и Dc - подвижности и коэффициенты диффузии электронов (с = e), одноатомных (с = i 1) и двухатомных ионов (с = i2), соответственно, Qio« – интенсивность объемной ионизации внешним источником, Р1 = Pph + Р3 «e — суммарный коэффициент рекомбинации электронов и одноатомных ионов аргона, Ph - коэффициент фоторекомбинации и Р — коэффициент трехтельной электрон-ионной рекомбинации, в — коэффициент рекомбинации электронов и двухатомных ионов аргона, k3i – константа скорости процесса конверсии одноатомных ионов аргона в двухатомные, ф - потенциал самосогласованного поля, «с - концентрация плазменных частиц с-сорта, nAr - концентрация атомов аргона. Отметим, что ионизацией собственными электронами плазмы в несамостоятельных разрядах можно пренебречь [10].

На систему (1) наложим следующие граничные условия [7], [8]:

n-_r=г = 0, «ie_г = 0, «_Щг=г = 0, I ^{r r} 0                                     l r ^r 0                                       l r ^r 0

^{дф 5 r} V = r ₀ = - eq int /^ , « e^ = „ = « e 0 ,         (4)

«i1|r=™ = n10 , ni2|r=™ = n20 , фг=m = 0, где r0 – радиус макрочастицы, ne0, n10, n20 – концентрация электронов и ионов в невозмущенной плазме, qint – заряд макрочастицы, найденный интегрированием потоков на нее:

t qint ( t ) = 4ПГ02 J(je - j11 - j2 )|r=r0 dt .        (5)

Концентрация заряженных частиц в невозмущенной плазме определяется системой уравнений:

Q ion ^{+ V} ₁₀ n n e 0 - ( P ph ⁺ Р з ne 0 ) n e 0 « 10 - ^в 2 ne 0 ^П 20 = ⁰,

V3 «10 - P2 «e0 «20 = 0,

«e 0 «20 «10 0, где Vion = kion«Ar, v3 = k3,.«A. Из последних двух уравнений находим:

n = P2 «e0  n = V3«£0

«10 о , , «20     о , . •

^P 2 « e 0 ^{+ V} 3           ^P 2 « e 0 ^{+ V} 3

Подставив эти решения в первое уравнение системы (6), для нахождения концентрации электронов получим алгебраическое уравнение 4-й степени:

^P 2 ^P 3 « e ⁴0 ^{+ P} ph ^P 2 « e ³0 ^{+ P} 2 ( ^V 3 ^{- V} ion ) «^0 -

^- ( ^P 2 ^Q .o« ^{+ V} ion ^V 3 ) « e 0 ^{- V} 3 ^Q .o« = ⁰

Согласно правилу знаков Декарта, это уравнение имеет единственное положительное решение. Этот вывод справедлив и в случае, когда трехтельной электрон-ионной рекомбинацией и/или фоторекомбинацией можно пренебречь (когда и P = 0, и P ph = 0, требование устойчивости плазмы приводит к неравенству v ₃ >  V _ion).

В стационарном состоянии система уравнений (1) принимает вид:

^div j e = ^Q ion ^{+ V} ion n e ^— ( ^P ph ^{+ P} 3 n e ) n e n !

^P 2 neni 2 ,

^div ^j i 1 = ^Q ion ^{+ V} ion n e ^- ( ^P ph ^{+ P} 3 n e ) n e n ! ^{— V} 3 n 1 , ⁽⁹⁾ div ^j , 2 = V з n i ^{— p} 2 ⁿ e n , 2 .

Нас будет интересовать асимптотическое поведение эффективного потенциала на расстояниях r >>  r ₀, когда все коэффициенты в (9) можно считать независящими от координат [15], [16]. Так как эффективный потенциал является убывающим с расстоянием, начиная с некоторого радиуса R_l можно провести линеаризацию уравнений (9). Пусть выполнены соотношения Эйнштейна:

D e = T e k _e e ^, здесь T e , T i 1 ,

D T D T

^D i 1 = T i 1 D i 2 = T i 2 k i 1 ek i 2 e

T i 2 – температура электронов и

ионов в энергетических единицах (если соотношения Эйнштейна не выполняются, что обычно имеет место для электронов в разрядных условиях, то под температурой будем подразумевать характеристическую энергию eD _c k^k_a ).

Линеаризуем систему, используя выражения для потоков в диффузионно-дрейфовом приближении (3) и соотношения Эйнштейна (10):

эффективными величинами, значения которых в рамках развиваемой теории не могут быть найдены [15], [16]. Их можно найти, сопоставляя результаты теории с результатами численных расчетов, что будет сделано ниже. Отметим, что потоки частиц плазмы зависят от заряда макрочастицы, поэтому q , S_e , S_{i 1} и S_{i 2} не являются независимыми величинами.

Применив к уравнениям (11), (12) трехмерное интегральное преобразование Фурье

^U c k = J ^Uc ( r ) exP ( ^{i k} • r ) ^d r •

Ф =J Ф( r) exp (i к • r) dr и проведя небольшие алгебраические преобразования, получим:

( к + an ) Ue к + a12 Ui 1k + a13Ui 2k = b1 • a 21Ue к + ( k + a 22 ) Ui 1k + a 23Ui2k = Ь2,      О4)

a 31 ^U e k ⁺ a 32 ^U i 1 k ^{+ ( k +} a 33 ) ^U i 2 k = ^Ь 3 •

® k = n ( U ^ + U i 2 k — U e k + q ) .      (15)

T А ф — A и = —

( ^P ph ^{+ 2 Р} 3 n e 0 ) n 10 ^{- V} ion

e

P ph + Р з n e 0

D     n e 0 u 1

e

D e

^Ue ^—

Здесь введены обозначения:

2 _ 4ne ² n e 0     2 _ 4ne ² n_w      2 _ 4ne ² n 20.

^k de        T 1 ^kd 1       T , ^kd 2       T ;

T e                  T i 1                  T i 2

P S

D ( n e 0 u 2 ⁺ n 20 u e ) ^— D ⁵ ( r ) ^,

Р

a К 2 + Vim + P2 n 20 a ^_p +M0 a11 ^de +     ^      • a12 d-de + d • ee

— en o. А ф — а и =

T

e

( ^P ph ^{+ 2 P} ne 0 ) n 10 ^{— V} ion

e

в

^P ph ^{+ P} 3 n e 0

_D      n_{e 0} u ₁

в

V

3 u

D

1 —

D i 1

%^{5( r} * ,

^Ue ^—

eno xa x V

--²⁰ А ф -A u, = —— u, ■

T i 2                D i 2

- ST ⁵ ( r ) •

D i 2

Аф = —4ne (u1 + и 2

в

Р

— ( n e 0 ^и 2 ^{+ n} 20 u e )

D i 2

— ue) — 4neq5( r),

в

(12) частиц

где и _с = и _с ( r ) - отклонения плотности сорта с т от равновесных значений вследствие по-

глощения плазмы макрочастицей и воздействия ее электрического поля и _с ( r ) = n _a ( r ) — n _{0 с} . Для учета граничных условий на границе плазма – макрочастица здесь введены стоки электронов и ионов S _CT 5 ( r ) , а также заряд макрочастицы eq 5 ( r ) , где 5 ( r ) - дельта-функция. В стационарном состоянии сток электронов и суммарный сток

П       2 I P2ne0  h — к2 n  ° n    —V I Vim a13    kde + d • b1 kdeq  Se • a21 kd 1 + q • n 2 , P1 ne 0 + V3 n 1 2 h 2„_°, a 22 = kd 1 + p^ • a 23 = kd 1 • b2 kd 1 q Si 1 •

D i 1

,^{2    p} 2 n ²⁰        ,2 _2^

a 31      d d 2 ⁺_л • a 32 d d 2 px •

D i 2                D i 2

a 33 = ^k d 2 ⁺ ^ L e ⁰ , b 3 = ^{— k} d 2 ^{q —} S i ² • ^S e = S e / D e • D _{i 2}

°_я = S V D 1 , S i 2 = S^D^ , P 1 = P ph + P 3 n e 0 ,

^V im = ( ^P ph ^{+ 2 P} 3 ne 0 ) n 10 ^— V on .

Детерминант системы уравнений (14) определяется выражением:

D = k ⁶ + a , k ⁴ + a 2 k ² + 0 3 ,             (16)

ионов равны друг другу:

S e = S 1 + S .,

но при зондовых измерениях они могут и не совпадать. Отметим, что введенные здесь заряд и стоки не равны истинным, а являются некими

где o^1 = ац + a 22 + a 33, a2 = an a 22 — a12 a 21 + an a 33 — — aj3 a 31 + a 22 a 33 — a 23 a 32.

(Z 3 = a_n a 22 a 33 ^— a_n a 23 a 32 + a j2 a 23 a 31 ^— a 12 a 21 a 33 + a 13 a 21 a 32 ^— a 13 a 31 a 22 .

Ис пользу я определения коэффициентов a_ik ( i — 1,3; k — 1,3), найдем:

U_{i 1 k} — D ¹ [ b 2 k 4 + ( b 2 a _n + b 2 a ₃₃ — b a ₂₁ — b 3 a ₂₃ ) k 2 +

„ 2 , n e 0 ⁺ ^ 2 n 20 , A n e 0 ^{+ V} 3 , ^в 2 n e 0

C a i       kJ   I                              I                           I ,

1d D DD ei1i2

^{+ b} 1 ^{( a} 31 ^a 23    ^a 21 ^a 33 ^{) + b} 2 ^{( a} 11 a 33    ^a 13 ^a 31 ^{) +}

^{+ b} 3 ⁽ a 21 ^a 13    ^a11 a 23 ) ] ,

« 2 = ^k de

P 1 ne 0 ^{+ V} m ^{+ V} 3 + P 2 ( n e 0 ⁺ n 20 )

D 1 D 2

U ii _{2 k} = D ¹ [ b ₃ k 4 + ( b ₃ a _u + b ₃ a ₂₂ - b 1 a ₃₁ - b ₂ a ₃₂ ) k ² +

⁺ k ²

P 1 n e 0 ^{+ V} m ⁺ P 2 n 20    ^в 2 n e 0 ^{+ V} 3

+ b 1 ( a ₂₁ a ₃₂ - a ₂₂ a ₃₁ ) + b ₂ ( a ₃₁ a ₁₂ - a_n a ₃₂ ) + (23)

D

D 2

+

^{+ b} 3 ^{( a} 11 ^a 22    ^a 21 ^a 12 ) ] .

^{+ k}d 2

V m ⁺ P 2 ( n e 0 ⁺ n 20 )    P 1 n e 0 + V 3

На основе (21)–(23) находим:

+

D e

P 1 P 2 n e 0 n 20 ^{+ V} 3 ( ^V m

D 1

+

U 1 k

^{+ U} 2 k ^-

Bk ⁴ + B₂k ² + B₃ / — ¹²³

k D ,

D e D 1

V m P 2 n e 0 , P 2 n e 0 ⁽ P 1 n e 0 ^{+ V} 3 )

+

D e D 2

D 1 D 2

,

« 3 =[ ^V m ( ^V 3 ⁺ Р 2 n e 0 ) ⁺

^{+ в} 2 ⁽ n e 0 ⁺ n 20 ^{)( V} 3 ⁺ Р 1 n e 0 ) J ^X

где

B 1 =- b + b ₂ + b ₃,               (25)

B ₂ — - b 1 ( a 21 + a 22 + a 31 + a 33 ) +

+ b 2 ( an + a 12 - a 32 + a 33 ) +            (26)

+ b 3 ( an + a 13 + a 22 - a 23 ) ,

^B 3 = b 1 ⁽ a 21 a 32 ^- a 21 a 33 ^{- a} 22 a 3 1 ^- a 22 a 33 ⁺ a 23 a 3 1 ⁺ a 23 a 32 ^{) +}

X

k de + k d 1 + k d 2

DD DD DD

1 2 e 2 e

^{+ b} 2 ⁽ a 11 a 33 a 11 a 32 ^{+ a} 12 a 31 ⁺ a 12 a 33 a 13 a 31 a 13 a 32 ^{)+    (27)}

^{+ b} 3 ⁽ a 11 a 22   a 11 a 23    a 12 a 21   a 12 a 23 ⁺ a 13 a 21 ⁺ a 13 a 22 ^{) .}

.

коэф-

Так как V im >  0 , отсюда видно, что все коэффициенты кубического уравнения относительно k ² уравнения (16) положительны, поэтому со-

Подставив последнее выражение в (15), Фурье-образ потенциала в случае трех различных

постоянных экранирования представим в виде:

гласно правилу знаков Декарта оно не имеет положительных действительных корней. В общем случае анализ уравнения (16) затруднен вследствие громоздкости коэффициентов. Проведен-

4 n e ^ф к =      q ⁺

1^1 + 2^2 + 3Я3          o\ k2 + k12 k2 + k22 k2 + k32 J,      ’

где коэффициенты C ₁, C ₂, C ₃ являются решением системы:

ные численные расчеты в аргоне при изменении давления в диапазоне 0,001–1 бар и скорости ионизации газа от 1012 до 1020 см–3с–1 показали, что все корни этого уравнения действительны и, соответственно, отрицательны, поэтому детерминант можно представить в виде:

D = ( k ² + k 2 )( k ² + k 2 )( k ² + k 2 ) . (20)

C_x k 1 + C 2 k 2 + C 3 k 3 ² = B„

/ 7 2 7 2 \ 7 2     ./72 7 2 \ 7 2     ./72 7 2 \ 7 2 n rw

| ( k 2 + k 3 ) k 1 C 1 + ( k 1 + k 3 ) k 2 C 2 + ( k 1 + k 2 ) k 3 C 3 — B 2 , (29)

Отсюда ясно, что экранирование в плазме с двумя сортами положительных ионов в общем случае будет определяться тремя постоянными, которые можно найти аналитически, но мы не будем выписывать эти выражения, так как для реальных вычислений они малопригодны ввиду невысокой точности получаемых решений. Поэтому постоянные экранирования в настоящей работе будем находить численными методами.

Решения системы линейных уравнений (14) имеют вид:

U_{e k} — D — 1 [ b k 4 + ( b i a 33 + b i a 22 — b 2 a ₁₂ — b ₃ a ₁₃ ) k 2 +

k²k ₂ ² k ₃ ² ( C 1 + C ₂ + C ₃ ) — B ₃.

Коэффициенты (25)–(27) через параметры плазмы выражаются следующим образом:

B 1 — - qk d + S e - ° 1 - S i2 ,           (30)

B 2 ^— ( ^{Se qk} de )

P 1 ne 0 ^{+ V} im ^{+ V} 3 ₊ P 2 ⁽ n e 0 ⁺ n 20 )

D i 1                D i 2

( ° , 2 \

S i 1 ^{+ qk} d 1 )

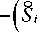
+ b 1 ( a ₂₂ a ₃₃ - a ₂₃ a ₃₂ ) + b ₂ ( a ₁₃ a ₃₂ - a ₁₂ a ₃₃ ) + (21)

^{+ b}3 ⁽ a 12 a 23    a 13 ^a 22 ) ] ,

P 1 ne 0 ^{+ V} im ^{+ в} 2 n 20 ₊ ^в 2 ne 0 ^{+ V} 3

D e              D i 2

^V im ⁺ P 2 ( n e 0 ⁺ n 20 ) ₊ P 1 П_е 0 + V 3

D e              D i 1

B3 — - q [Vim (V3 + P2 ne 0 ) +

+ P2 (ne0 + n20 )(V3 + P1 ne0 )]

k de        k d 1

² k_{d 2}

D i 1 D i 2 D e D i 2 D e D i

- (31)

Сравнение последнего выражения с коэффициентом a ₃ уравнения (16) показывает, что

B ₃ — - q a ₃ ^ - qkd k ₂ ² k ₃ ² .

Решениями системы (29) являются:

C1 =

( k 22 - k 32 )( B 1 k 1⁴ - B 2 k 2 + B ₃ )

D 0 k 1²

C

( ^k 32 - ^k 12 )( ^B 1 ^k 2 - D ₀ k ₂

B ₂ k ₂ ² +

B з )

C 3 =

( k 1² - k 22 )( B 1 k ₃ ⁴ -

D ₀ k ₃

B ₂ k ₃ ² + B ₃ )

а возможность появления таких постоянных экранирования в плазме определяется условиями:

a ₂ = 3 a 1² ,        a ₃ = ( f a 1 ) 3 .           (42)

Далее рассмотрим частные случаи, которые реализуются в различных приложениях и для которых можно получить простые аналитические решения для постоянных экранирования.

2. ЭКРАНИРОВАНИЕ ПРИ БОЛЬШИХ И МАЛЫХ СКОРОСТЯХ КОНВЕРСИИ ИОНОВ

где 42  2   42  2   42  2

о **"1 ^2      **'3      + A-2 '*3      ••'1      + **'3 **'1        a-2 .

Выполнив обратное Фурье-преобразование, из (28) находим:

ф ( r ) = -( q + C 1 + C ₂ + C ₃ - C 1 e - ^k ' r - C ₂ e - ^k2r - C ₃ e - ^k3r ) . (35)

Из последнего уравнения системы (29) и выражения (33) следует, что

C 1 + C ₂ + C ₃ =- q .

Поэтому окончательно из (35) находим

ф ( r ) = - e ( C 1 e ^{- k} 1 ^r + C ₂ e ^{- k} 2 ^r + C 3 e ^{- k 3 r} ) . (36) r

В случае двух совпадающих постоянных экранирования, то есть при наличии кратных корней уравнения (16), будем иметь (совпадающие постоянные обозначим как k 2 и k 3 : k 2 = k 3 ):

ф ( r ) = - 1 [ Ce - ^k - r + C 2 e - ^k 2 r + C 3 ( 1 +{ k ₂ r ) e - ^k 2 r ] , (37)

где

B k 1⁴ - B 2 k 1² + B 3

Cl             /            \ 2 , k2 (k2 - k22 )2

B 1 k ₂ ² ( k 22 - 2 k 1² ) + B ₂ k 1² - B ₃

k 2 ( k 1² - k 2 )

C ,= B 1 k 2 - B 2 k 22 + B 3

• ³       k ₂ ⁴ ( k 1² - k ₂ ² ) .

  
  

В случае трех совпадающих постоянных экранирования ( k 1 = k 2 = k 3 ) потенциал макрочастицы будет описываться выражением:

ф ( r ) = - eqe - ^k 1 ^r ( 1 + C 2 k 1 r - C " kr ² ) ,     (39)

r где

C” =

C 2

7 B 1 k 1⁴ - 3 B ₂ k 1² - B ₃ 8 qk ₁ ⁶

„ B,k, - B~k, + B₃

C" = —---2r---3.(40)

• 3        8qk16

• 2.1.    Большая скорость конверсии ионов

В случае трех одинаковых постоянных экранирования они равны:

k1 = k2 = k3 = 3 a1,(41)

При высоких давлениях для не очень плотной и/или холодной плазмы, когда выполнено условие в2ne0 << k3nL,                 (43)

рекомбинацией одноатомных ионов можно пренебречь. В этом случае n ₁₀ ® 0, k d 1 ~ 0 и n ₂₀ ® n _{e 0} = n ₀. Также положим, что k ion = 0, так как при высоких давлениях устойчиво и однородно горит только несамостоятельный газовый разряд с внешним источником ионизации газа, в котором самостоятельная ионизация пренебрежимо мала [10] (см. также [3], [5], [6]). Теперь из (16) находим:

I l2 ^ 3 ^{+ в} 1 ^{n 0} | Г 1⁴ , 3,2 / т_2 т_2 \ т_2 т_2 т,2 т,2 "1

I ^{k +} р^ Н_ ^{k + k} ( ^kd ^{+ k}s ) ^{+ 2} k se k de ^{+ 2 k}si^kd 2 ] ^,(44) V          D i1 7

где kS = kSe + ks2 , kse = в2 n 0 I De , ks2 = в2 n 0 ID2 . Один из корней уравнения (44) дает постоянную экранирования k3 = 7 (v3 + в1n 0 )/D1 .

Легко показать из (34), что коэффициент C3 в (36) для этой постоянной в рассматриваемом случае равен нулю. Из выражения в квадратных скобках (44) для двух других постоянных экра- нирования находим:

ki,2 = 12 (kd + ks )±

2                            (46)

1 22    22   22

±-^ 4 (kd + ks )    2ksekde 2ksikdi , где kd2i = k(22, в рассматриваемом случае kd2i = 4ne2n0 [T22. Выражение (4б) совпадает с полученным в работах [15], [16]. Отметим, что в изотермической плазме для рассматриваемого случая возможно появление двух одинаковых постоянных экранирования (подробнее см. в [15], [16]).

• 2.2.    Малая скорость конверсии ионов

Теперь рассмотрим случай, когда конверсией одноатомных ионов в двухатомные можно пренебречь. Этот случай реализуется при выполнении противоположного (43) условия, например при высоких температурах газа, так как константа трехчастичной конверсии ионов с ростом температуры падает как T-3 [20] или при низких давле- ниях газа. В этом случае n20 ®0, kd 2 ®0, n10 re ne0 = n0, и из (16) для детерминанта находим:

' к 2 + tee Jr к 4 ₊ к 2 ( к^ к-. + k -) +

I      D 2 J ^L                             (47)

+ к2 (k2.+ kV)+kdn (k2.+ ^e)], где ^ = Vm^D , к2 = vjD, , kp. = в n о/D. , крi = P1 n0 /Di 1 . Одна из постоянных экранирования равна:

к 3 = V в 2 n 0 D ,             (48)

но, как легко показать из (34), коэффициент C 3 в (36) для этой постоянной равен нулю. Здесь мы не будем приводить общее решение для двух других постоянных экранирования, а рассмотрим более частные случаи, когда можно пренебречь фоторекомбинацией и когда можно пренебречь трехтельной рекомбинацией.

Далее ограничимся рассмотрением изотермической плазмы, в которой к /. = к /21 = у к 2 . Тогда из (46) для постоянных экранирования в плазме с внешним источником ионизации газа при v ion = 0 (с учетом ^к / . = ² Р 3 n 02 D , ^{к 2}= ² Р 3 n 02 / D i , ^к ,2 . = ^в 3 ⁿ 02 / ^D e , ^к ,2 . = ^в 3 ⁿ 0 / ^D , 1 ) получим:

k 1²

= 1 ²

к / + в 3 n 02

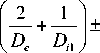
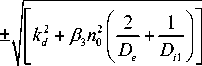
6 к / в 3 n 02

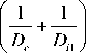
Так как всегда выполнено условие D e >>  D_; ,

k ₁

-1 2 ^k2₊

1,2 2 2 ^{к/ +}

2.2.1. Малая скорость фоторекомбинации

Этот случай, в котором в 1 = в ₃ n 0 , v _im = 2 в 3 n 2 - v ion , реализуется в достаточно плотной плазме, когда трехтельная рекомбинация преобладает, то есть при выполнении условия

Р з П о >> в ph .                   (49)

Например, в термической плазме концентрация электронов и ионов определяется соотношением Саха [9]:

n e 0 n0 _ gg. ^{2 2 n mT} T² J I Ar = 2 exp

П аг     g a I h 2 J I T

= A—T ^3/2 exp C I A. J , g a        I ^T J

где A = 4,85 х 10¹⁵ см^-3К^-3/2 = 6,06 х 10²¹ см " ³эВ " ^3/2 [9], g i – статистический вес иона (для Ar⁺ g i = 6), g a – статистический вес атома (для Ar g a = 1), h – постоянная Планка, I Ar – потенциал ионизации атомов ( I Ar = 15.76 эВ), T – температура газа в энергетических единицах. Сопоставляя выражения для коэффициентов рекомбинации, представленные в табл. 1, и используя (50), можно определить критическую температуру, при которой скорости двух рассматриваемых процессов рекомбинации сравняются друг с другом. При атмосферном давлении в чистом аргоне это произойдет при температуре газа, равной ~0.5 эВ. При более низкой температуре в процессах гибели электронов будет преобладать фоторекомбинация. Если в термической плазме будут присутствовать атомы

щелочных металлов с низким потенциалом ионизации, то граничная температура будет существенно меньшей.

В плазме несамостоятельного разряда при T e = T i = 0.0258 эВ фоторекомбинацией можно пренебречь при скоростях ионизации газа внешним источником, превышающих 10⁵ см^–3с^–1. С ростом электронной температуры граничная скорость ионизации также растет.

Р 3 ⁿ 02 ]

D , 1 ^J

2 k d ²

P 3 ⁿ 02

D i 1

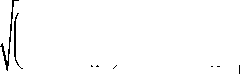
Р 3 ⁿ 02

D

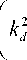
Из (51) видно, что возможно появление комплексных постоянных экранирования при выполнении условия

2 k d ²

P 3 n 02

Di 1

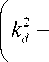
P 3 ⁿ 0 | D i J .

Выражение (52) представим в виде:

₂ к ° , p 3 n 0 >2 к ! - p 3 ⁿ 0 J ²

ⁿ 0 ^D 1   I ⁿ 0    ^D 1 J

Величина k_d ² n ₀ не зависит от концентрации электронов и ионов, поэтому при заданной температуре T левая часть (53) с ростом скорости ионизации газа линейно растет, причем эта зави-

симость проходит через начало координат, а правая часть (53) падает. Следовательно, эти кривые обязательно пересекутся, и это произой-

дет при скорости ионизации газа

8 ( 2 - Vs ) P 1³ L

1L ion 2

P 3

где в 1 _L = 4 п .к i 1 - коэффициент рекомбинации Ланжевена одноатомных ионов. При дальней-

шим увеличении скорости ионизации условие (52) начнет нарушаться после достижения

Q ion

8 ( 2 + Л ) ³ P 1³ L ²

P 32

На рис. 1 приведены зависимости критической скорости ионизации газа, согласно (54), от температуры изотермической плазмы. На этом графике также приведена кривая потерь одно-

атомных ионов за счет конверсии в двухатомные, которые, как видно на рисунке, на несколько порядков меньше потерь в процессе трехтельной рекомбинации (практически совпадающих со скоростью ионизации газа). Потери за счет фоторекомбинации при этих скоростях ионизации газа оказались пренебрежимо малыми. Из рис. 1 видно, что условие (53) может быть выполнено только при очень высоких скоростях ионизации газа, недостижимых на практике. Также нужно отметить, что при таких высоких скоростях ионизации газа температура электронов будет существенно отличаться от газовой и ионной температур.

Далее рассмотрим термическую плазму ( T e = T il = T), в кото рой Q on = 0 . Теперь ^v _lon = Р з П 2 или n o = \^{V /} / ^в , V = k e = в з 4 D e , ^ = ^ 8 = ^в n o7 ^D ' Для определения постоянных экранирования из (47) получаем уравнение :

к ⁴ + ^{k 2} ( ^ 2 + Р ^ e + ^к в i ) + ^k dl ( ^к в e + ^0i ) = ⁰ . ⁽⁵⁵⁾

Из (55) находим : 2222  2

k1 kd , k2 kpe + kpi , то есть одна из постоянных экранирования совпадает с дебаевской. В этом случае возможно равенство к1 = к2. Найдем параметры термической плазмы, при которых это равенство будет иметь место:

Tn = в з n 2

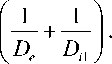
Так как D e >>  D i , отсюда получим:

^e n ⁰ D ~ в з n o или 2 p_L « в з n o , ⁽⁵⁶⁾ где в_L = 4 nek i ₁ - ланжевеновский коэффициент рекомбинации одноатомных ионов. Оценки с использованием соотношения Саха показывают, что равенство (56) возможно только при очень высоких давлениях. В этой области параметров приведенные в табл. 1 зависимости вряд ли применимы.

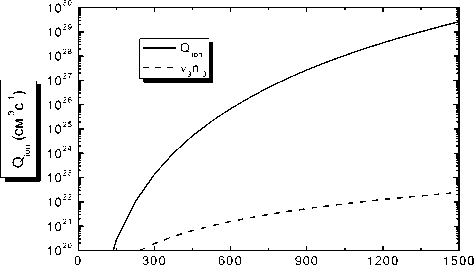
T (K)

Рис. 1. Значения критической скорости ионизации газа в зависимости от температуры при концентрации газа N = 2,5 х х 10¹⁷ см^-э, согласно (54), выше которых появятся комплекс -ные значения постоянных экранирования

• 2.2.2.    Малая скорость трехчастичной рекомбинации

• 3. ЧИСЛЕННЫЕ РАСЧЕТЫ ПОСТОЯННЫХ ЭКРАНИРОВАНИЯ И ПРОЦЕССА ЗАРЯДКИ МАКРОЧАСТИЦ

В этом случае # = в , v _im = в ⁿ 0 ^- V ion , и ^из (47) в обозначениях [15], [16], [22], [23] получим:

к 4 + к 2 (£2 + kS - ^ ) + + kde (2 к2- к2 ) + к21 ( 2 к2 - к2 ) = 0, где к.2е = (врЬ n0 — V,on )/De = к2е — к,2 ,

V = ( ^в ph П 0 — ^V ion )/ D 1 = ^к ^ — ^{к 2} , ^к в e = ^к2е , к ² -' = ^к^ .

Это выражение совпадает с полученным в работах [15], [16], [22], [23] уравнением для нахождения постоянных экранирования в двухкомпонентной плазме.

Для проверки полученных результатов проведем численные расчеты зарядки пылевых частиц. Систему нестационарных уравнений (1)– (2) с граничными условиями (4) будем решать численно, методом конечных разностей [7], [8]. В качестве внешней границы будем использовать сферу с радиусом, равным радиусу ячейки Зейтца – Вигнера

А—^1/з. a d = ( У ^ n d ) :

n e|_r = a d = n e 0 , n 1 |_r = _a d = n 10 , n - 2 | _r = _a d = n 20 ,

4-_a = 0,

¹ r = ^a d

где nd – концентрация макрочастиц, которая выбиралась такой, чтобы исключить влияние внешней границы на результаты расчетов. Концентрации электронов и ионов в невозмущенной плазме находились численно из системы (6). В качестве начальных данных задавались нулевые значения потенциала во всей ячейке, и в большинстве расчетов полагалось, что ячейка Зейтца – Вигнера заполнена плазмой с равновесной концентрацией.

Расчеты проведены для аргона, коэффициенты переноса электронов в котором были рассчи- таны на основе численного решения уравнения Больцмана для ФРЭЭ с сечениями из [24]. При Te = 300 K подвижность и коэффициент диффу- зии электронов при концентрации атомов аргона nAr = 2,5 х 1019 см-3 равны: ke = 9,98 х 104 см2/(В с), De = 2580 см2/с. При Te = 300 К = 0,026 эВ, Qion = 1014 см–3с–1 коэффициенты рекомбинации равны: Р2 = 8,5 х 10-7 смз/с, вРь = 4,188 х 10-12 смз/с, вТ= 1,22 х 10-19 см6/с,^1 = 1,з29 х 10-9 смз/с.При атмосферном давлении коэффи- циенты переноса ионов равны (T = 300 К) [11]: к-1 = 1,з0 см2/(В с), Di1 = з,зб4 х 10-2 см2/с, к,2 = 2,094 см2/(В с), D,2= 5,419 х 10-2 см2/с.

Температура электронов во всей расчетной области полагалась постоянной; соответственно, полагались постоянными все коэффициенты переноса и рекомбинации. Более подробно методика расчета заряда макрочастиц описана в [7], [8].

На рис. 2 приведены начальные распределения электронов и ионов в расчетной ячейке и установившиеся, стационарные распределения. Видно, что возмущение, вызванное поглощением электронов и ионов пылевой частицей радиусом 1 микрон, простирается на сотни микрон. Также видно, что даже при таком низком давлении, как 103 Па, концентрация молекулярных ионов уже превышает концентрацию атомарных.

На рис. 3 представлены зависимости заряда макрочастицы от времени при трех разных давлениях. Видно, что с уменьшением давления время выхода заряда на стационарный уровень также уменьшается, что обусловлено ростом коэффициента амбиполярной диффузии ионов с уменьшением давления, в то время как характерный размер области нарушения квазинейтральности плазмы вокруг макрочастицы, пропорциональный дебаевскому радиусу экранирования, слабо зависит от давления. Поэтому характерное время пересечения ионом области пространственного заряда вокруг пылевой частицы с уменьшением давления уменьшается и время формирования пространственного профиля концентрации ионов также уменьшается.

На рис. 4, 5 приведены зависимости потенциала от расстояния до центра макрочастицы, полученные в численном расчете и согласно асимптотической теории экранирования. Из рис. 4, 5 видно, что расчетный потенциал хорошо описывается суперпозицией трех экспонент с постоянными экранирования, вычисленными из (16). С увеличением давления, как видно из сравнения рис. 4 и 5, наименьшая постоянная экранирования также растет и потенциал макрочастицы при более высоком давлении быстрее спадает с расстоянием.

В табл. 2 представлены постоянные экранирования и коэффициенты C 1 , C 2 и C 3 зависимости (36) потенциала от расстояния, вычисленные из выражений (34) с использованием полученных в численном расчете значений заряда и стоков электронов и ионов для разных давлений аргона при T e = 0,028 эВ. Также приведены значения этих коэффициентов, найденные сравнением расчетных распределений потенциалов (см. рис. 4, 5) с кривыми, полученными из зависимости (36). При расчете распределений потенциала из (36) использовались полученные из формулы (16) постоянные экранирования. Видно, что с ростом давления согласие между полученными двумя способами значениями коэффициентов улучшается и при атмосферном давлении они практически совпадают друг с другом. Отличие коэффициентов связано с отмеченным выше обстоятельством, что заряды и стоки в модели точечных стоков являются некими эффективными величинами, которые отличаются от истинных и в рамках асимптотической теории

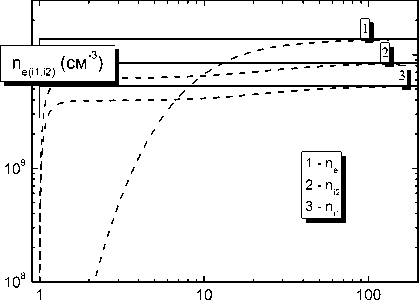
r (мкм)

Рис. 2. Зависимости концентрации электронов и ионов от расстояния до частицы:

При давлении 10³ Па в аргоне при Q ion = 10¹⁴ см^–3с^–1, T e = 300 K, n d = 10³ см^–3: сплошные линии – в момент времени t = 0, пунктирные линии – стационарные распределения при t = 100 мкс; n e – концентрация электронов, n i 1 – концентрация атомарных и n i 2 – концентрация молекулярных ионов

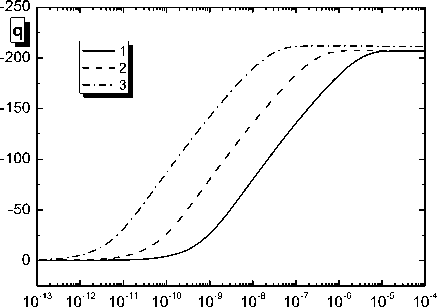
Рис. 3. Эволюция заряда макрочастицы во времени в аргоне при разных давлениях: 1 – 10⁵ Па, 2 – 10⁴ Па, 3 – 10³ Па

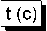
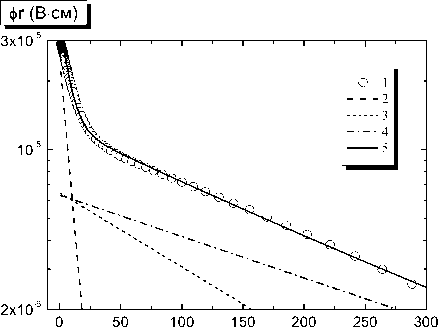
r (мкм)

Рис. 4. Зависимости потенциала от расстояния до частицы при давлении 103 Па:

1 – расчетные точки (три раза прорежены), 2 – распределение потенциала с первой постоянной экранирования, 3 – со второй, 4 – с третьей, 5 – их сумма

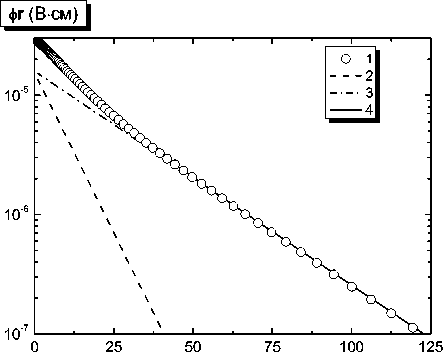
r (мкм)

Рис. 5. Зависимости потенциала от расстояния до частицы при давлении 105 Па:

1 – расчетные точки (два раза прорежены), 2 – распределение потенциала со второй постоянной экранирования,

3 – с третьей, 4 – их сумма (распределение с первой постоянной экранирования в данном масштабе проходит значи тельно ниже оси абсцисс)

Таблица 2

Постоянные экранирования и коэффициенты C ₁ , C ₂ и C ₃ зависимости (36) потенциала от расстояния при T e = 0,0258 эВ

p, бар		0.01	0.1	1
k sh 1	Численное решение (16), см–1	0,1391	0,2361	7,466
k sh 2		7,480 х 10 - 3	0,1232	0,1232
k sh 3		4,182 х 10 - 3	1,305 х 10 - 2	4,125 х 10 - 2
C 1	Из (34)	133,617	1,969 х 10 - 2	- 1,984 х 10 - 7
	Из численных расчетов	175	^^^^^в	^^^^^в
C 2	Из (34)	- 0,1044	125,531	106,295
	Из численных расчетов	45	140	106,295
C 3	Из (34)	77,961	81,699	100,621
	Из численных расчетов	44	83	110

не могут быть найдены. Из табл. 2 также видно, что с ростом давления коэффициент C1 становится, как и отмечалось выше, пренебрежимо малым (в численных расчетах постоянные экранирования пронумерованы по убыванию, поэтому С1 соответствует ksh1, который при высоких давлениях практически совпадает с k3, вычисленной из (45) (см. рис. 4, 5)).

На рис. 6–8 приведены зависимости постоянных экранирования от давления аргона при

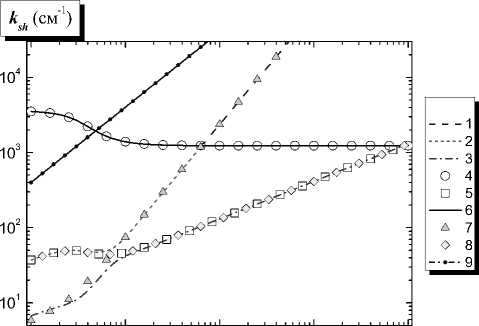
10 ^-3             10 ^-2             10 ^-1              10 ⁰              10 ¹

p (10⁵ Па)

Рис. 6. Зависимости постоянных экранирования от давления аргона при T_e = 0,0258 эВ: 1 – k_{sh 1} , 2 – k_{sh 2} , 3 – k_{sh 3} , 4 – k ₁ из (46), 5 – k ₂ из (46), 6 – k_d , 7 – k ₃ из (45), 8 – k ₃ из (48), 9 – l_{i 1} ^–1

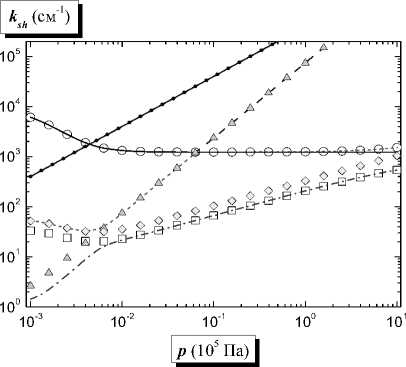
Рис. 7. Зависимости постоянных экранирования от давления аргона при T e = 0.1 эВ. (Обозначения, как на рис. 6.)

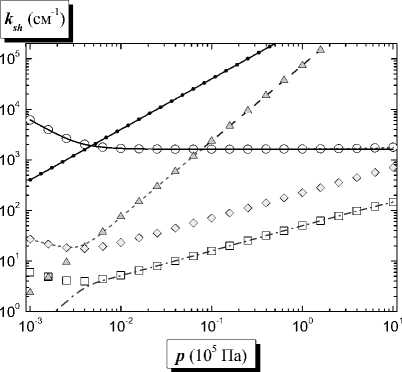
Рис. 8. Зависимости постоянных экранирования от давления аргона при T e = 1 эВ. (Обозначения, как на рис. 6.)

скорости ионизации газа Q ion = 10¹⁴ см^–3с^–1. Численные решения уравнения (16) обозначены как k sh 1 , k sh 2 и k sh 3 . Особое внимание обратим на то, что постоянные экранирования в исследованном диапазоне давлений нигде не пересекаются (см. рис. 9, где представлены области сближения зависимостей k sh 1 и k sh 2 в увеличенном масштабе), то есть уравнение (16) в этом диапазоне не имеет совпадающих корней. Величины k 1 и k 2 рассчитаны из соотношения (46), а k 3 – из (45) и (48).

Из анализа рис. 6–8 можно сделать следующие выводы:

• 1.    Одна из постоянных экранирования практически совпадает с дебаевской;

• 2.    Есть диапазон давлений, примерно от 10³ до 10⁴ Па, где все три постоянные экранирования сравнимы друг с другом;

• 3.    Постоянные экранирования в плазме с одним сортом положительных ионов практически совпадают с двумя постоянными экранирования в двухионной плазме;

• 4.    Выражение (45) хорошо описывает одну из постоянных экранирования, а (48) – описывает ее же, но только в изотермической плазме или только при низких давлениях.

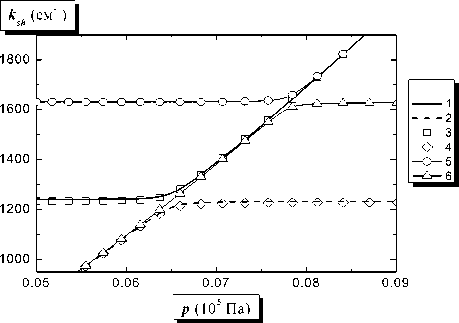
Рис. 9. Зависимости постоянных экранирования от давления аргона при T e = 0,0258 ( 1, 2 ), 0,1 ( 3, 4 ) и 1 эВ ( 5, 6 ): 1, 3, 5 – k_{sh 1} , 2, 4, 6 – k_{sh 2}

Растущая зависимость первой постоянной экранирования после области сближения, отмеченной кружочком, объясняется процессом конверсии ионов, скорость которой растет квадратично с давлением. Эта постоянная экранирования в данной области определяется выражением (46) и, следовательно, растет с ростом давления газа. Но, как уже отмечалось выше, коэффициент в (36) при этой постоянной экранирования в этой области мал, к тому же на малых расстояниях линеаризированная теория вряд ли применима.

В заключение обсудим вопрос об области применимости использованной в настоящей работе гидродинамической модели зарядки. Уравнения непрерывности для положительных ионов применимы при выполнении условий:

l i 1 = L , l i 2 = L ,                   (59)

где l i 1 , l i 2 – длина свободного пробега одноатомных и комплексных ионов соответственно, L – характерный размер задачи. На рис. 6–8 приведены зависимости обратной длины пробега одноатомных ионов аргона от давления, ниже которых применимо диффузионно-дрейфовое приближение для описания переноса ионов (при низких давлениях основным сортом ионов являются одноатомные ионы). Из рис. 6–8 видно, что при давлениях выше 10³ Па условия (59) для всех постоянных экранирования выполнены. Что касается электронной компоненты, то зависимость постоянных экранирования от коэффициентов переноса электронов практически отсутствует, поэтому изменением подвижности и коэффициента диффузии электронов в окрестности макрочастицы можно пренебречь. Константы скоростей рождения и гибели электронов и ионов (которые зависят от температуры электронов), как было показано в работе [14], практически не зависят от расстояния до поверхности пылевой частицы, поскольку температура электронов в области нарушения квазинейтральности плазмы меняется незначительно. Это является следствием высокой теплопроводности электронной компоненты по сравнению с коэффициентом амбиполярной диффузии, формирующей область пространственного заряда (более подробно см. в [14]). Поэтому изменением констант скоростей также можно пренебречь. Итак, мы можем сделать окончательный вывод о том, что использованная в настоящей работе гидродинамическая модель зарядки применима при выполнении условий (59).

ЗАКЛЮЧЕНИЕ

В настоящей работе на основе модели точечного стока получен вид экранированного потенциала макрочастицы в плазме с двумя сортами положительных ионов. Численно получены значения постоянных экранирования в плазме с внешним источником ионизации газа. Установлено, что при наличии ионов двух сортов выражение для распределения потенциала в окрестности заряженной макрочастицы является суперпозицией трех экспонент в общем случае с тремя разными постоянными экранирования. Численные расчеты показали, что одна из постоянных экранирования близка к дебаевской. При повышенных давлениях коэффициент при экспоненте с наибольшей постоянной оказывается пренебрежимо мал, к тому же сама экспонента быстро затухает на малых расстояниях. Также установлено, что две из трех постоянные экранирования во всем исследованном диапазоне параметров плазмы практически совпадают с постоянными экранирования в плазме с одним сортом положительных ионов. Также показано, что есть диапазон давлений, где оказываются важными все три экспоненты.

Работа выполнена при финансовой поддержке РФФИ, грант № 07-02-00504-а.